Задания предназначены для подготовки к олимпиаде по математике
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Олимпиадные задания по математике 11 класс
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Олимпиадные задания по математике 11 класс»
Полезное для учителя
Распродажа видеоуроков!
1900 руб.
3170 руб.
1720 руб.
2860 руб.
1540 руб.
2560 руб.
1720 руб.
2860 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
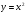 пересекает координатные оси Ox и Oy в точках A и B так, что
пересекает координатные оси Ox и Oy в точках A и B так, что 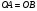 . Найдите длину отрезка AB.
. Найдите длину отрезка AB.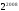 и
и 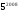 выписаны одно за другим в десятичной записи. Сколько всего цифр выписано?
выписаны одно за другим в десятичной записи. Сколько всего цифр выписано?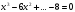 . Какое уравнение должно было быть записано на доске и каковы его корни?
. Какое уравнение должно было быть записано на доске и каковы его корни?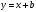 или
или 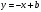 , поэтому в точках касания
, поэтому в точках касания 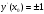 , т.е.
, т.е. 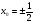 . Уравнение касательных в точках
. Уравнение касательных в точках 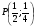 и
и 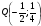 :
: 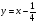 и
и 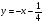 . Следовательно
. Следовательно 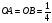 , откуда
, откуда 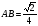 .
.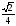 .
.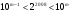 и
и 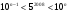 . Перемножив эти неравенства, получим
. Перемножив эти неравенства, получим 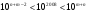 . От сюда следует, что искомое число цифр
. От сюда следует, что искомое число цифр 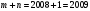 .
.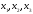 - корни многочлена, тогда
- корни многочлена, тогда 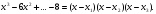 Перемножив двучлены в правой части и прировняв коэффициенты при одинаковых степенях
Перемножив двучлены в правой части и прировняв коэффициенты при одинаковых степенях  получим:
получим: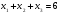 (1)
(1)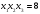 (2)
(2)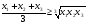 , причем равенство возможно тогда и только тогда, когда
, причем равенство возможно тогда и только тогда, когда 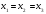 . Из равенств (1) и (2)
. Из равенств (1) и (2) 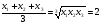 . Это означает, что
. Это означает, что 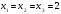 и значит, уравнение можно записать так:
и значит, уравнение можно записать так: 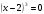 или
или 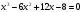 .
.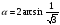 , то центральный угол, опирающийся на дугу образованную одним шнурком сетки, равен
, то центральный угол, опирающийся на дугу образованную одним шнурком сетки, равен  . Обозначив радиус шара
. Обозначив радиус шара  , получим
, получим 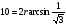 . Значит
. Значит 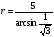 .
.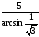 см.
см. - количество участников турнира. Каждый из них сыграл
- количество участников турнира. Каждый из них сыграл 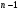 партию, всего на турнире было сыграно
партию, всего на турнире было сыграно 
















