1 Решите уравнение 3x+5+(x+5)=(1−x)+4
2 Решите уравнение 8−5(2x−3)=13−6x
3. Решите уравнение 10x+9=7x
4 Решите уравнение 3x+10=8x
5 Решите уравнение − x−2+3(x−3)=2(4−x)−3
6 При каком значении x значения выражений 7x−2 и 3x+6 равны?
7 Решите уравнение x+2−4(x−2)=5(3−x)+3
8 Решите уравнение 10(x−9)=7
9 Решите уравнение 9(x−5)=− x
10 Решите уравнение − 9(8−9x)=4x+5
11 Решите уравнение 4x+4−3(x+1)=5(− 2−x)+5
12 Решите уравнение 6x+13=x
13 Решите уравнение 1−5x=− 6x+8
14 Решите уравнение 9−2(− 4x+7)=7
15 Решите уравнение 6(5−x)=− 8x−7
16 При каком значении x значения выражений 2x−4 и 6x+8 равны?
17 Решите уравнение 2x+2=− 3
18 Решите уравнение x−3−4(x+1)=5(4−x)−1
19 Решите уравнение 1−7(4+2x)=− 9−4x
20 Решите уравнение 9+10(3x−10)=2
21 Решите уравнение 9(x−6)=4x
22 Решите уравнение 10(x+4)=9x
23 Решите уравнение 10x+1=− 8
24Решите уравнение 4(x−7)=3x
25 Решите уравнение − 3x+1−3(x+3)=− 2(1−x)+2
26 Решите уравнение 2−3(2x+2)=5−4x
27 Решите уравнение 4x+7=0
28 Решите уравнение − 7−2x=− 6x+10
29 Решите уравнение 2+3x=− 7x−5
30 Решите уравнение − 2x+5+4(x−1)=− 4(− 4−x)+3
31 Решите уравнение − 5x−6=0
32 Решите уравнение 2x−4−3(x−4)=− 2(− 3−x)−4
33 Решите уравнение 4(x−6)=5
34 Решите уравнение 5(x+4)=− 9
35 Решите уравнение 5(x−7)=9x
36 Решите уравнение 3(x−8)=5x
37 Решите уравнение − 3x+1+(x−5)=5(3−x)+5
38 Решите уравнение 5x−8=0
39 Решите уравнение 5x+2=5
40 Решите уравнение − 1−10x=− 9x+1
41 Решите уравнение 4(x−8)=− 5
42 Решите уравнение − x+4+(x−5)=− 2(− 2−x)+5
43 Решите уравнение 5x+4=0
44 Решите уравнение 7+8x=− 2x−5
45 Решите уравнение − 4x+3=0
46 Решите уравнение − 10x+2=0
47 Решите уравнение 4x−1=− 7
48 Решите уравнение 7+9(4x+5)=− 2
49 Решите уравнение − 6x+10=− 2
50 Решите уравнение 2x+2+3(x+4)=− 4(1−x)+3
51 Решите уравнение − 5+2x=− 2x−3
52 Решите уравнение − 3x−3+5(x−4)=2(− 5−x)−1
53 Решите уравнение − 4x+10=− 5
54 Решите уравнение − 2x−9=− 1
55 Решите уравнение − 5x−2+4(x+1)=4(− 3−x)−1
56 Решите уравнение 7+5(− 9x+7)=− 3
57 Решите уравнение 1−10x=5x+10
58 Решите уравнение − x−4+5(x+3)=5(− 1−x)−2
59 Решите уравнение − 4+7x=8x+1
60 Решите уравнение − 4x+8=10
61 Решите уравнение x+3+2(x+3)=− 5(5−x)+4
62 Решите уравнение x+3+2(x+3)=− (3−x)+4
63 При каком значении x \значения выражений 3x−2 и 2x+4 равны?
64 Решите уравнение − 8x+10=0
65 Решите уравнение 5x−9=0
66 Решите уравнение − 4−6x=4x−3
67 Решите уравнение − 5x+7=− 10
Решите уравнение 6x+2=− 1




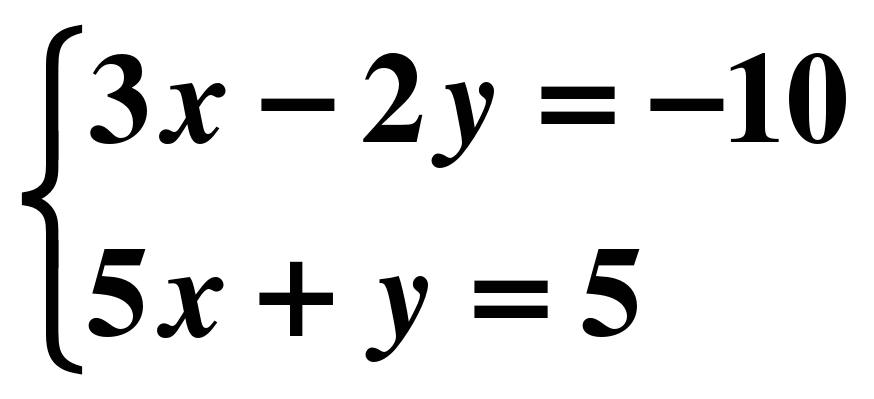
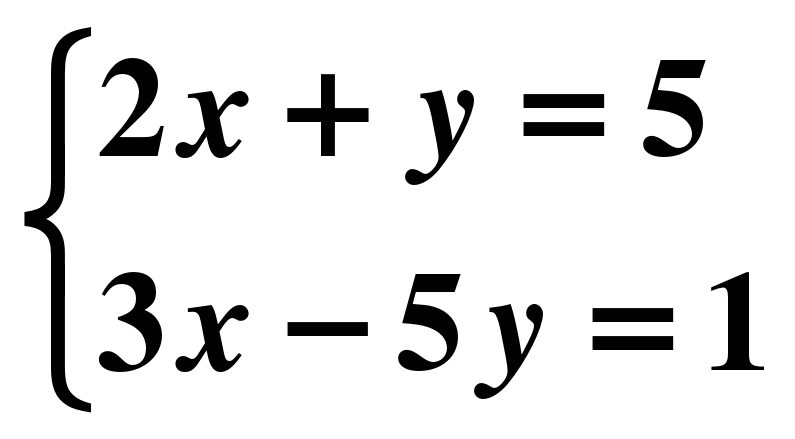

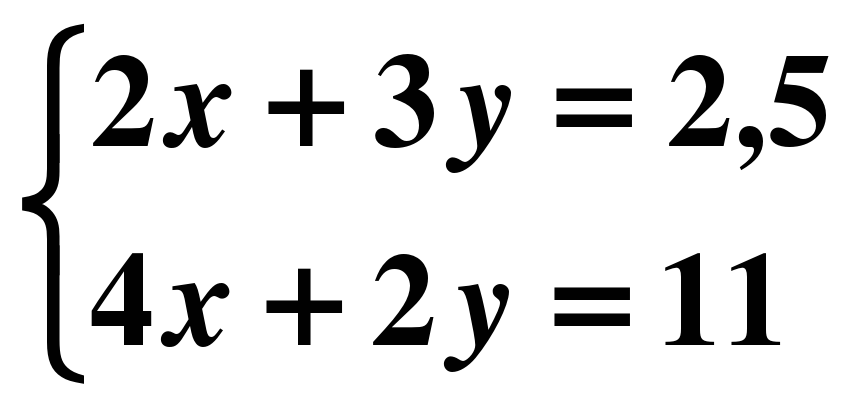
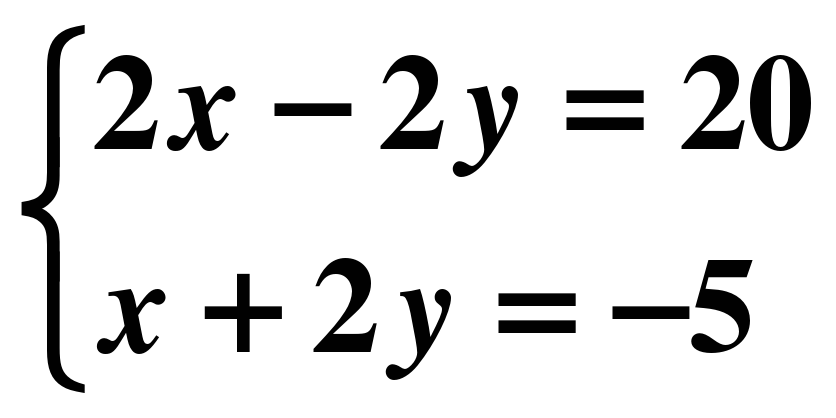
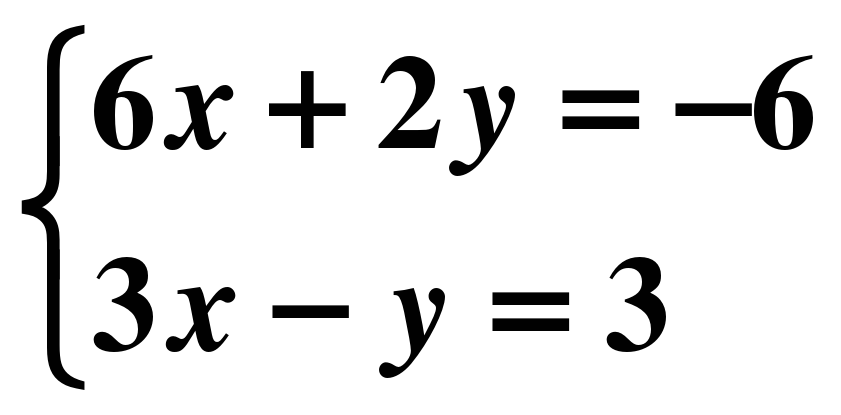

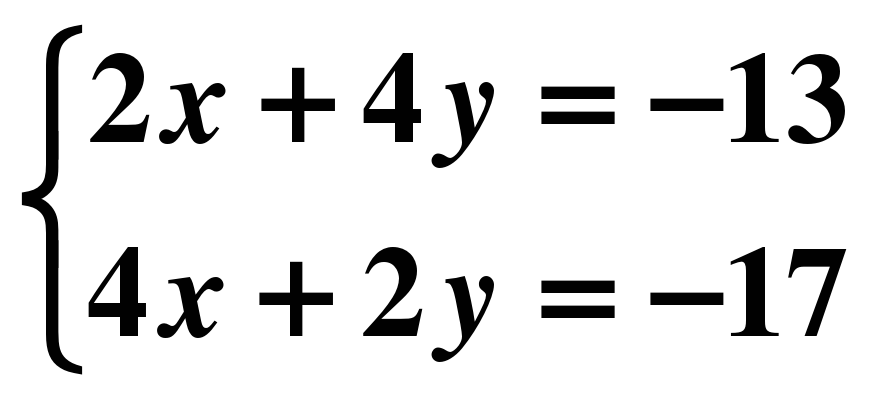
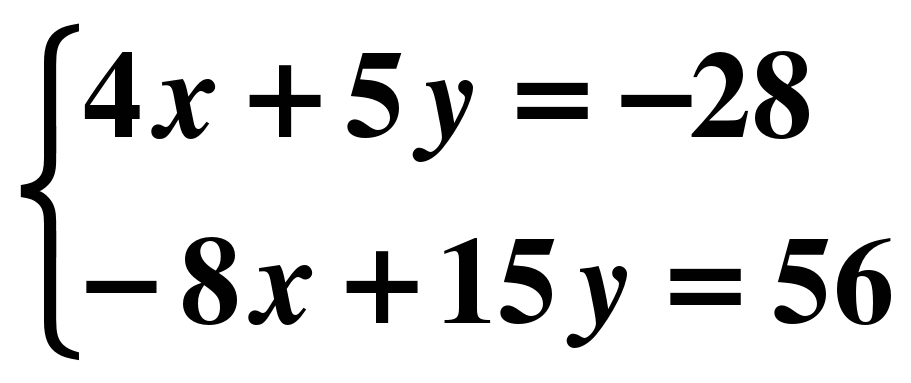
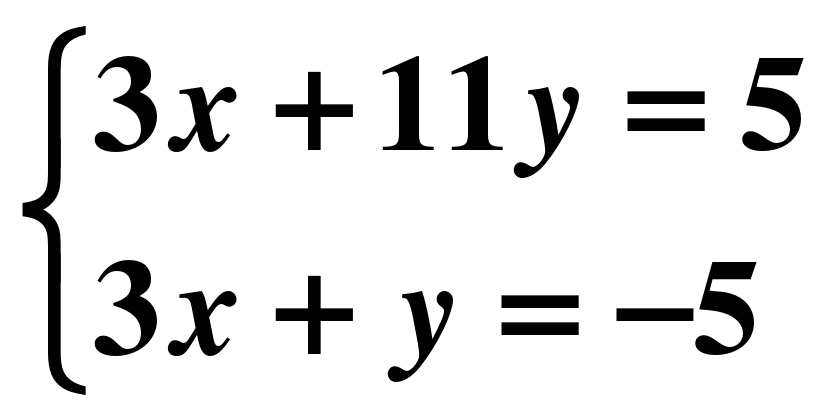


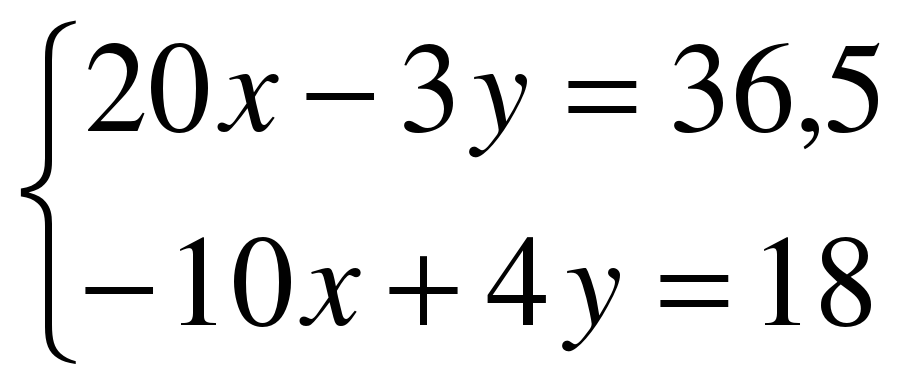
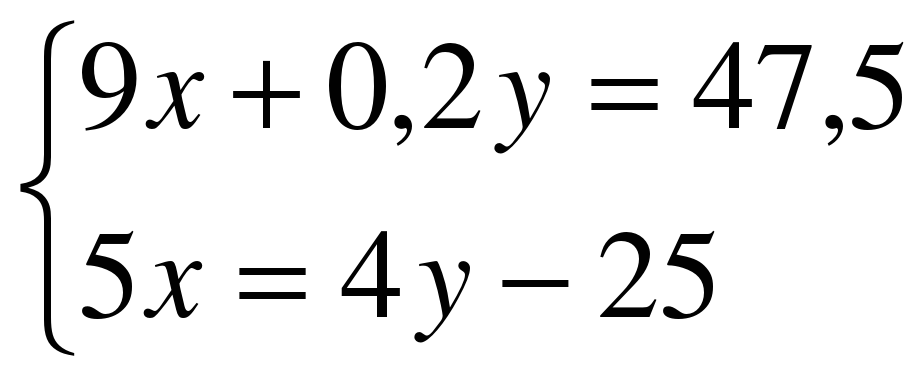
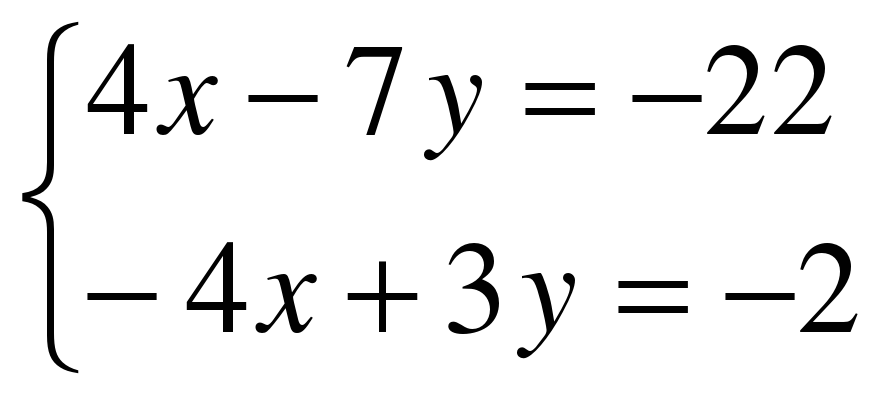
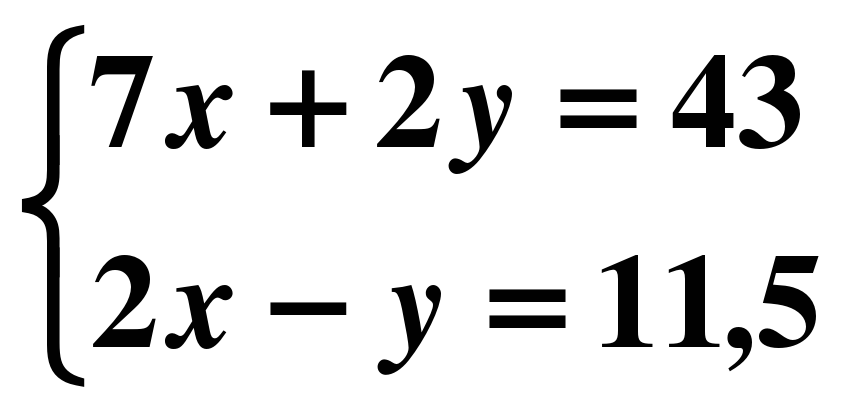

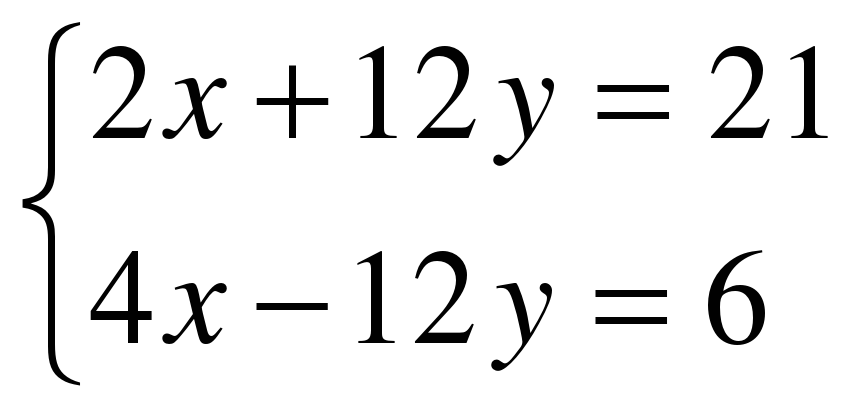
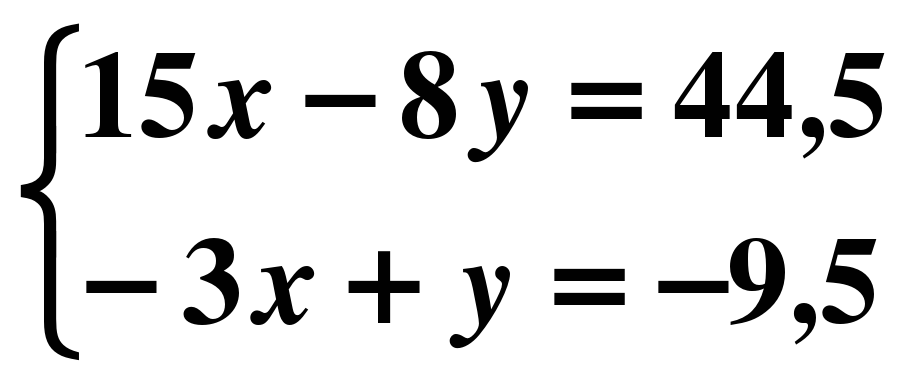
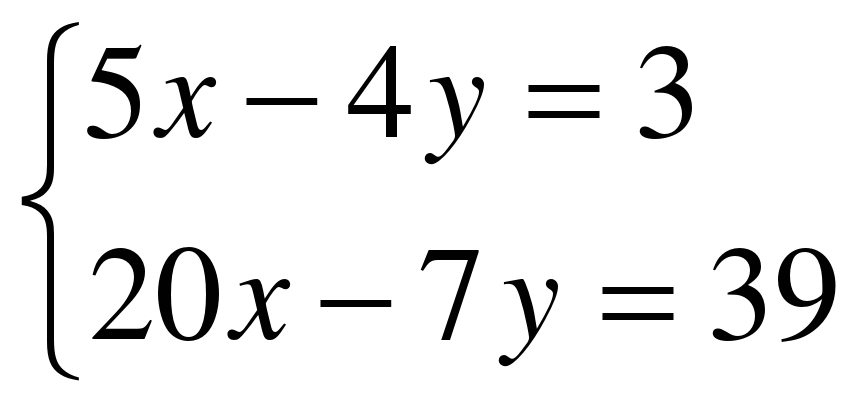


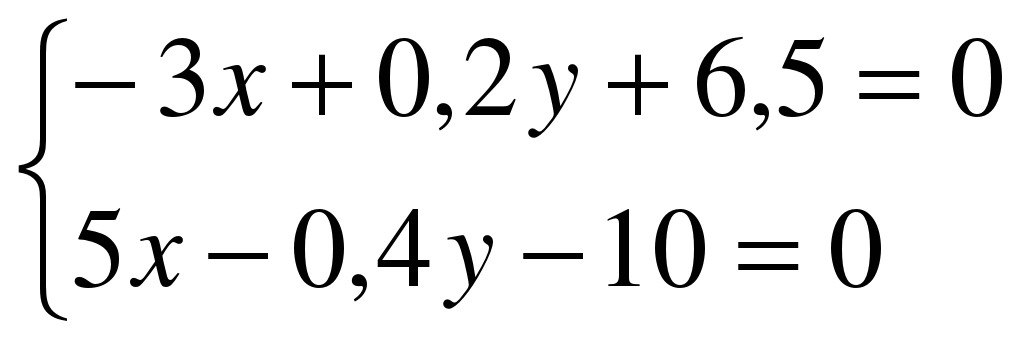
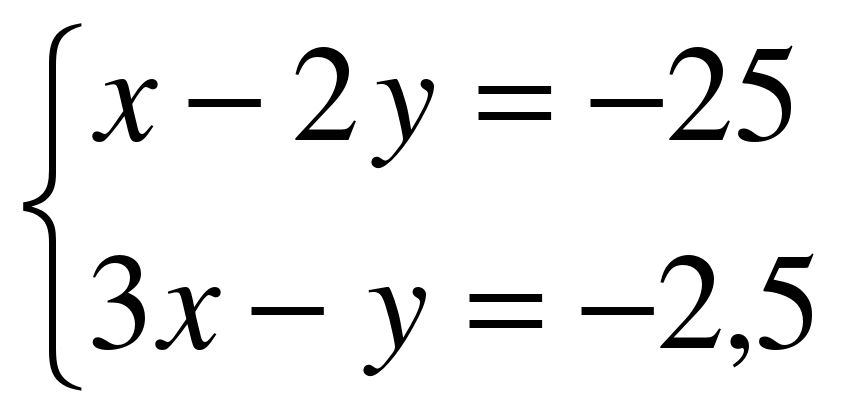


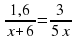

 х=1 9) 16х-64=0
х=1 9) 16х-64=0 10) -3(х+1)+8=
10) -3(х+1)+8=