Курсовой проект

Министерство образования и молодёжной политики Свердловской области

Государственное автономное профессиональное образовательное учреждение

Свердловской области

«Камышловский педагогический колледж»

Курсовой проект

Профессиональный модуль ПМ 01 Преподавание по программе начального общего образования в начальных классах и начальных классах компенсирующего и коррекционно-развивающего образования

Технология проблемного обучения как средство достижения предметных результатов по разделу «Нумерация чисел» на уроках математики

в начальной школе

44.02.05.Коррекционная педагогика в начальном образовании

Составитель:

Шубина Т.В.,

студентка 3КП группы

Руководитель:

Анциферова Л.В.,

преподаватель

Камышлов, 2020

Оглавление

Пояснительная записка 1

Актуальность, цели, задачи курсового проекта 1

Психолого-педагогические основы проблемного обучения 4

Возможности использования технологии проблемного обучения как средства достижения предметных результатов по разделу «Нумерация» на уроках математики в начальной школе 12

Анализ имеющегося педагогического опыта использования технологии проблемного обучения для достижения предметных результатов по разделу «Нумерация» на уроках математики в начальной школе 19

Анализ УМК «Школа России» и «Перспектива» с позиции выявления возможности применения технологии проблемного обучения для достижения предметных результатов по теме «Нумерация» на уроках математики в начальной школе 25

Общая характеристика компонентов методической разработки 31

Обоснование способов оценки качества методической разработки, показателей успешности ее реализации 34

Подборка конструктов уроков по математике с использованием технологии проблемного обучения как средства достижения предметных результатов по теме «Нумерация чисел» на уроках математики в начальной школе 37

Заключение 45

Список литературы 47

Приложение 52

Пояснительная записка

Актуальность, цели, задачи курсового проекта

XXI век – век высоких компьютерных технологий. Современный ребёнок живёт в мире электронной культуры. Сегодня обществу нужен не только человек, который много знает и умеет, но прежде всего человек, способный принимать самостоятельные решения, обладающий приёмами учения, готовый к самообразованию, умеющий жить среди людей, готовый к сотрудничеству для достижения совместного результата.

Актуальность исследования обусловлена наличием требований федерального государственного образовательного стандарта начального общего образования к результатам освоения основной образовательной программы.

В пункте 7 определен системно-деятельностный подход, который предполагает гарантированность достижения планируемых результатов освоения основной образовательной программы начального общего образования, что и создает основу для самостоятельного успешного усвоения обучающимися новых знаний, умений, компетенций, видов и способов деятельности [43].

Пункт 11. Метапредметные результаты освоения основной образовательной программы начального общего образования должны отражать освоение способов решения проблем творческого и поискового характера.

Процесс учения как творческий процесс включает в себя, прежде всего, открытие нового: новых объектов, новых знаний, новых проблем, новых методов их решения. При этом проблемное обучение как творческая деятельность представляет собой поиск решения нестандартных задач нестандартными методами. Если тренировочные задачи предлагаются учащимся для закрепления знаний и отработки навыков, то проблемные задачи - это всегда поиск нового способа решения.

Одним из перспективных направлений активизации учебной деятельности учащихся, развития у них познавательных интересов, творческих способностей, самостоятельности, исследовательских умений является проблемное обучение.

На основе анализа нормативных документов, психолого-педагогической, методической литературы и педагогического опыта определены следующие противоречия:

• между требованиями, предъявленными к результату образования, зафиксированными в федеральном государственном образовательном стандарте начального общего образования, и представленными результатами на практике использования данной технологии;

• между достаточным теоретическим изучением теорий проблемного обучения и использованием данной технологии на практике;

• между необходимостью создания различных технологий проблемного обучения и недостаточным количеством методических пособий, направленных на технологии проблемного обучения;

Работы известных психологов В.В. Давыдова, С.Ф. Жуйкова, Л.В. Занкова, Д.Б. Эльконина показали, что у младших школьников имеются значительные резервы и возможности психологического и педагогического развития, проявлению которых способствует проблемное обучение. Организация проблемных ситуаций в целом дает повышение эффективности обучения, они активизируют умственную деятельность большинства учащихся. Однако, среди методистов, психологов, педагогов нет единого мнения о том, можно ли сделать проблемный метод основным для начальных классов, пронизывающим весь процесс обучения [8].

Выявленные противоречия позволили определить проблему исследования: невозможность организовать процесс обучения таким образом, чтобы он соответствовал идеологии нового стандарта, что нужно применять учителю, чтобы ученики класса успешно выполнили те требования, которые будут предъявлены к их подготовке по завершении обучения в школе.

Реализация технологии проблемного обучения в школе является настоятельной потребностью современности, поскольку реалии сегодняшнего дня все больше требуют от человека умения решать проблемы, самостоятельно осуществлять выбор в сложившейся ситуации.

Важность и актуальность рассматриваемой проблемы, ее недостаточная теоретическая и практическая разработанность определили выбор темы исследования. Технология проблемного обучения как средство достижения предметных результатов по разделу «Нумерация чисел» на уроках математики в начальной школе.

В качестве предполагаемой формы курсового проекта является сборник конструктов по математике на тему «Нумерация чисел».

Объект исследования: процесс организации проблемного обучения младших школьников.

Цель исследования: определение возможности использования технологии проблемного обучения в начальной школе при изучении нумерации через создание и реализацию сборника конструктов уроков.

Задачи:

1. раскрыть психолого-педагогические основы технологии проблемного обучения, по средством анализа психолого-педагогической литературы;

2. проанализировать имеющийся педагогический опыт использования элементов проблемного обучения при изучении нумерации, а также УМК «Школа России» и «Перспектива», с позиции выявления возможности использования элементов проблемного обучения в начальных классах;

3. описать основные пути реализации проблемного обучения, способы оценки качества, показателей результативности ее реализации;

4. подобрать конструкты уроков по математике на тему «Нумерация чисел», с использованием элементов проблемного обучения.

Для решения поставленных задач применялся комплекс взаимодополняющих теоретических и эмпирических методов педагогического исследования. К методам теоретического исследования, использованным в работе, можно отнести: анализ психологической, педагогической деятельности, методической литературы, статей в специальных и периодических изданиях по внедрению в учебный процесс технологии проблемного обучения, сравнительно-исторический метод для сравнения традиционного обучения и проблемного обучения. Анкетирование, чтобы выявить, сколько учителей используют метод проблемного обучения и используют ли вообще, беседы с учителями, использующими технологию проблемного обучения на практике, метод экспертной оценки данными учителями.

Практическая значимость проекта заключается в том, что подборка конструктов уроков по изучению нумерации может быть использована учителями начальных классов для организации элементов проблемного обучения.

Курсовой проект состоит из пояснительной записки, практической части, включающей подборку конструктов уроков на тему «Нумерация чисел», с элементами проблемного обучения, списка литературы и приложений.

Психолого-педагогические основы проблемного обучения

Ещё в 19 веке немецкий педагог А. Дистервег говорил: «Сведений науки не следует сообщать учащемуся, но его надо привести к тому, чтобы он сам их находил, самодеятельно ими овладевал. Такой метод обучения наилучший, самый трудный, самый редкий». Ведущую роль отводил проблемному обучению известный советский педагог Ш.А. Амонашвили.

Поиски моделей, которые позволяли бы обучать критическому, продуктивному мышлению, привели к созданию проблемного обучения – одного из видов обучения, основанных на использовании эвристических методов – специальных методов, используемых в процессе открытия нового[2].

Концепция проблемного обучения получила широкое распространение, тем не менее, существует несколько подходов к ее трактовке.

Проблемное обучение – это совокупность таких действий как организация проблемных ситуаций, формулирование проблем, оказание ученикам необходимой помощи в решении проблем, проверка этих решений и, наконец, руководство процессом систематизации и закрепления приобретенных знаний (В. Оконь, 1986)[30].

Проблемное обучение – это такая организация учебных занятий, которая предполагает создание под руководством преподавателя проблемных ситуаций и активную самостоятельную деятельность учащихся по их разрешению, в результате чего и происходит творческое овладение профессиональными знаниями, навыками и умениями и развитие мыслительных способностей (Г. К. Селевко, 2006)[38].

М.И. Махмутов дает следующее определение понятия «проблемное обучение»: «Проблемное обучение - это тип развивающего обучения, в котором сочетаются систематическая самостоятельная поисковая деятельность учащихся с усвоением ими готовых выводов науки, а система методов построена с учетом целеполагания и принципа проблемности; процесс взаимодействия преподавания и учения ориентирован на формирование мировозрения учащихся, их познавательной самостоятельности, устойчивых мотивов учения и мыслительных (включая и творческие) способностей в ходе усвоения ими научных понятий и способов деятельности детерминированного системой проблемных ситуаций»[22].

В своём проекте мы опираемся на понятие М.И. Махмутова, т.е. на привитие самостоятельной поисковой деятельности учащимся, а в результате освоение ими готовых выводов наук. Мы будем придерживаться этого понятия, т.к. М.И. Махмутов наиболее чётко и полно описал суть проблемного обучения.

Каждое из определений раскрывает одну из сторон проблемного обучения, а в сумме подчёркиваются главные признаки, которые лежат в основе моделирования уроков в режиме технологии проблемного обучения: 1) создание проблемных ситуаций; 2) обучение учащихся в процессе решения проблем; 3) сочетание поисковой деятельности и усвоения знаний в готовом виде.

Из термина «проблемное обучение» вытекает термин «проблема». А что же такое проблема? Проблема - это задача, решение которой ориентировано не столько на достижение практического результата, сколько на выработку новой или рефлексию уже использующейся методологической позиции. Учебная проблема существует в двух основных формах: 1) как тема урока; 2) как несовпадающий с темой урока вопрос, ответом на который и будет новое знание. Следовательно, поставить учебную проблему - значит помочь ученикам самим сформулировать либо тему урока, либо не сходный с темой вопрос для исследования.

Главные психолого-педагогические цели проблемного обучения:

• развитие у учащихся способов мышления и интеллектуальных способностей;

• усвоение учащимися знаний и умений, добытых в ходе активного научного поиска и самостоятельного решения проблем (при этом освоенные знания и умения являются более прочными, чем при традиционном обучении);

• воспитание активной, творческой личности учащегося, умеющего видеть, ставить и разрешать нестандартные проблемы;

• развитие у обучающихся рефлексивных умений и критического мышления.

Исходя из задач начальной школы, выделяют основные функции проблемного обучения. Их делят на общие и специальные.

Общие функции проблемного обучения:

• усвоение учащимися системы знаний и способов умственной и практической деятельности;

• развитие познавательной самостоятельности и творческих способностей учащихся;

• формирование диалектико-материалистического мышления школьников как основы их мировоззрения.

Специальные функции:

• воспитание навыков творческого усвоения знаний (применение логических приемов или отдельных способов творческой деятельности);

• воспитание навыков творческого применения знаний (применение усвоенных знаний в новой ситуации и умение решать учебные проблемы);

• формирование и накопление опыта творческой деятельности (овладение методами научного исследования, решение практических проблем и художественного отображения действительности).

Суть проблемной интерпретации учебного материала состоит в том, что учитель не сообщает знаний в готовом виде, но ставит перед учащимися проблемные задачи, побуждая искать пути и средства их решения. Проблема сама прокладывает путь к новым знаниям и способам действия.

Проблемное обучение является не абсолютно новым типом обучения в опыте педагогической практики, в прошлом с ним связаны такие известные имена как Сократ, Руссо, Дистерве, Ушинский и др.[18].

Проблемное обучение основывается на теоретических положениях американского философа, психолога и педагога Дж. Дьюи, основавшего в 1894 г. в Чикаго опытную школу, в которой учебный план был заменён игровой и трудовой деятельностью. Занятия чтением, счетом, письмом проводились только в связи с потребностями - инстинктами, возникавшими у детей спонтанно, по мере их физиологического созревания. Технология проблемного обучения получила распространение в 20-30-х годах в советской и зарубежной школе. Возникновение дидактической системы проблемного обучения в советской педагогике связывают с исследованиями: Л.В. Занкова(организация содержания и построение процесса обучения), М.А. Данилова (построение процесса обучения), М.Н. Скаткина, И.Я. Лернера(содержание и методы обучения), Н.А. Менчинской и Е.Н. Кабановой-Меллер(построение системы приёмов познавательной деятельности), Т.В. Кудрявцева и А.М. Матюшкина(построение процесса научения), В. В. Давыдова и Д. Брунера(организация содержания) и М.И. Махмутова(построение процесса обучения).

Выдвинув идею новой дидактической системы, Л.В. Занков представил её как сочетание новых дидактических принципов, построенных с учетом закономерностей соотношения обучения и развития (младших) школьников, экспериментально доказал преимущество новой схемы учебного процесса над традиционной. Дальнейшее развитие новая дидактическая система получает в исследованиях В. В. Давыдова, который обосновал необходимость иметь новую структуру содержания учебного материала, построенную на основе сочетания современной формальной логики с логикой диалектической[10].

Сравнив два подхода к обучению: традиционный и проблемный, можно определить основные отличия двух подходов. (Приложение 1 Сравнительная характеристика проблемного и традиционного обучения). Главным отличием двух видов обучения следует считать целеполагание и принцип организации педагогического процесса.

Основным отличаем проблемного обучения от традиционного является характер организации учебного процесса.

При традиционном обучении учитель сообщает факты, сам анализирует их и, применяя наглядность, объясняет сущность новых понятий, сам формулирует определение новых теорем, правил, законов и так далее. Здесь доминирует информационное изложение учебного материала учителем, и нет преднамеренного создания проблемных ситуаций.

При проблемном обучении деятельность учителя состоит в том, что он, давая в необходимых случаях объяснение содержания наиболее сложных понятий, систематически создает проблемные ситуации, сообщает учащимся факты и организует их учебно-познавательную деятельность. На основе анализа фактов учащиеся самостоятельно делают выводы и обобщения, формулируют (с помощью учителя) определение понятий, правила, или самостоятельно применяют известные знания в новой ситуации[9].

При проблемном обучении учитель систематически организует самостоятельные работы учащихся по усвоению новых знаний, умений, повторению изученного материала и отработке навыков. Учащиеся сами добывают новые знания, у них вырабатываются навыки умственных операций и действий, развиваются внимание, творческое воображение, догадка, формируется способность открывать новые знания и находить новые способы действия путем выдвижения гипотез и их обоснования.

Проблемное обучение, создает наиболее благоприятные условия для формирования таких необходимых современному человеку качеств, как познавательный интерес, творческая активность. В процессе проблемного объяснения материала возникает проблемная ситуация, которая составляет отношение между усвоенным и новым и вызывает у ученика стремление самому найти ответы на возникающие вопросы, а не «зубрить» бездумно правило.

Важнейшей чертой содержательного аспекта проблемного обучения является отражение объективных противоречий, закономерно возникающих в процессе научного знания, учебной или исследовательской деятельности. Именно в связи с этим проблемное обучение можно назвать развивающим, так как, его цель – освоение учениками знаний и обобщенных умений посредством решения так называемых учебных задач. При проблемном же обучении учащиеся включаются в разрешение проблемной ситуации, при этом у них формируются способы действий, необходимые для решения нестандартных задач.

Важная особенность проблемного обучения - это специфическая интеллектуальная деятельность ученика по самостоятельному усвоению новых понятий путем решения учебных проблем, что обеспечивает сознательность, глубину, прочность знаний и формирование логико-теоретического и интуитивного мышления. Только прочное знание становится действительным достоянием школьников, которые они могут осознанно применять в своей дальнейшей теоретической и практической деятельности.

Ещё одна особенность состоит в том, что проблемное обучение – наиболее эффективное средство формирования мировоззрения, поскольку в процессе проблемного обучения складываются черты критического, творческого и диалектического мышления. Самостоятельное решение проблем учащимися является и основным условием превращения знаний в убеждения, так как только диалектический подход к анализу всех процессов и явлений действительности формулирует систему прочных и глубоких убеждений [39].

Связь с жизнью служит важнейшим средством создания проблемных ситуаций и критерием оценки правильности решения учебных проблем.

Систематическое применение учителем наиболее эффективного сочетания разнообразных типов и видов самостоятельных работ учащихся. Указанная особенность заключается в том, что учитель организует выполнение самостоятельных работ, требующих как актуализации ранее приобретенных, так и усвоения новых знаний и способов деятельности.

В проблемном обучении используется принцип индивидуального подхода. Наличием учебных проблем разной сложности, которые каждым учеником воспринимаются по-разному. Индивидуальное восприятие проблемы вызывает различие в ее формулировании, выдвижении многообразных гипотез и нахождении иных путей их доказательства.

Динамичность проблемного обучения заключается в том, что одна ситуация переходит в другую естественным путем на основе диалектического закона взаимосвязи и взаимообусловленности всех вещей и явлений материального мира.

Высокая эмоциональная активность ученика, обусловлена, во-первых, тем, что сама проблемная ситуация является источником ее возбуждения, во-вторых, тем, что активная мыслительная деятельность ученика неразрывно органически связанна с чувственно-эмоциональной сферой психической деятельности. Всякая самостоятельная мыслительная деятельность поискового характера, связанная с индивидуальным «принятием» учебной проблемы, вызывает личное переживание ученика, его эмоциональную активность. В свою очередь, эмоциональная активность детерминирует активность мыслительной деятельности[20].

Обеспечивает новое соотношение индукции и дедукции (усиление значения второго пути познания) и новое соотношение репродуктивного и продуктивного, в том числе творческого, усвоения знаний, повышая роль именно творческой познавательной деятельности учащихся.

Проблемное обучение не может быть одинаково эффективным в любых условиях. Практика показывает, что процесс проблемного обучения порождает различные уровни, как интеллектуальных затруднений учащихся, так и их познавательной активности и самостоятельности при усвоении новых знаний или применении прежних значений в новой ситуации. В соответствии с видами творчества можно выделить три вида проблемного обучения.

Первый вид («научное» творчество) – это теоретическое исследование, то есть поиск, и открытие ученикам нового правила, закона, теоремы и т.д. В основе этого вида проблемного обучения лежит постановка и решение теоретических учебных проблем.

Второй вид (практическое творчество) – поиск практического решения, то есть поиск способа применения известного знания в новой ситуации, конструирование, изобретение. В основе этого вида проблемного обучения лежит постановка и решение практических учебных проблем.

Третий вид (художественное творчество) – это художественное отображение действительности на основе творческого воображения, включающее в себя литературные сочинения, рисование, написание музыкального произведения, игру и т.д.

Итак, все виды проблемного обучения характеризуются наличием репродуктивной, продуктивной и творческой деятельности ученика, наличие поиска и решения проблемы. Они могут осуществляться при различных формах организации педагогического процесса. Однако первый вид чаще всего встречается на уроке, где наблюдается индивидуальное, групповое и фронтальное решение проблем. Второй – на лабораторных, практических занятиях. Третий вид – на уроке и на внеурочных занятиях[22].

Возможности использования технологии проблемного обучения как средства достижения предметных результатов по разделу нумерация на уроках математики в начальной школе

Использование элементов технологии проблемного обучения начинают постепенно с 1 класса. Делать это нужно систематически. И уже в 4 классе учащиеся привыкают к решению проблем на разных уроках, на это уходит меньше времени, и ученики грамотно, быстро определяются с темой и целью урока. Технология проблемного обучения состоит из двух частей: создание проблемы и решение этой проблемы. Создать проблему может учитель или сами учащиеся. Можно представить проблему в игровой форме, что повышает мотивацию детей к решению этой проблемы. В решении проблемы основными участниками являются ученики, учитель является наблюдателем и направляющим. При исследовании проблемы, учащиеся сравнивают, анализируют, выводят гипотезу, высказывают своё мнение, оспаривают его и т.д. Положительное, что на уроке каждый из учеников хочет первым найти решение проблемы.

Проблемная ситуация - центральное звено проблемного обучения, с помощью которого пробуждается мысль, познавательная потребность, активизируется мышление, создаются условия для формирования правильных обобщений. Создание проблемных ситуаций, определяющих начальный момент мышления, является необходимым условием организации процесса обучения, способствующего развитию подлинного продуктивного мышления детей, их творческих способностей.

«Чтобы создать проблемную ситуацию в обучении, - отмечает А.М. Матюшкин, - нужно поставить ребенка перед необходимостью выполнения такого задания, при котором подлежащие усвоению знания будут занимать место неизвестного»[19].

Проблемная ситуация специально создается учителем путем применения особых методических приемов:

• учитель подводит школьников к противоречию и предлагает им самим найти способ его разрешения;

• сталкивает противоречия практической деятельности;

• излагает различные точки зрения на один и тот же вопрос;

• предлагает классу рассмотреть явление с различных позиций;

• побуждает учеников к сравнению, обобщению, обоснованию, конкретизации и логике рассуждения;

• определяет проблемные теоретические и практические задания;

• ставит проблемные задачи с недостаточными или избыточными исходными данными, с неопределенностью в постановке вопроса, с противоречивыми данными, с заведомо допущенными ошибками, с ограниченным временем решения и др.

Именно проблемные ситуации дают возможность создать такую логику объяснения нового материала, которая отражает логику соответствующей науки, дидактически преломленную применительно к уровню мышления учащихся определенного возраста. Правильная логика объяснения нового материала, отражающая логику науки, способствует тому, что одна ситуация переходит в другую естественным путем, на основе взаимосвязи и взаимообусловленности вещей и явлений. Процесс мышления начинается с анализа проблемной ситуации. «В результате ее анализа возникает, формулируется задача, проблема в собственном смысле слова. Возникновение задачи - в отличии от проблемной ситуации - означает, что теперь удалось хотя бы предварительно и приблизительно расчленить данное (известное) и искомое (неизвестное). Это расчленение выступает в словесной формулировке задачи». Эти положения помогают определить пути организации проблемного обучения в школе. Проблемная ситуация должна создаваться с учетом реальных, значимых для учащихся противоречий. Только в этом случае она является мощным источником мотивации познавательной деятельности школьников, активизирует их мышление, направляет на поиск неизвестного. Это положение имеет принципиальное значение для практики проблемного обучения[1].

В самом общем виде проблемная методика характеризуется двумя основными чертами:

1) перед учащимися ставятся проблемы, в результате которых возникает проблемная ситуация - психологическое состояние, связанное с появлением неразрешенных вопросов и стремлений найти на них ответ;

2) при разрешении проблемы учащиеся получают не только сумму сведений, но и знакомятся с методами познания изучаемых в школе наук.

В дидактике разработаны такие требования к созданию проблемной ситуации:

1) содержать в себе определенную познавательную трудность, связанную с объективными противоречиями, свойственными изучаемому объекту;

2) вытекать из логики познавательного процесса;

3)содержать возможность последовательного ее членения, развертывания в вопросы, каждый из которых может являться ступенью в решении проблемы;

4) направлять учащихся на актуализацию тех знаний, которые необходимы для ее решения;

5) побуждать их к активному познавательному поиску, вызывать эмоциональное отношение к процессу поиска истины;

6) быть посильной для учащихся.

Основные условия для успешного применения проблемного обучения учителем следующие:

• проблемные ситуации должны отвечать целям формирования системы знаний;

• быть доступными для учащихся и соответствовать их познавательным способностям;

• должны вызывать собственную познавательную деятельность и активность;

• задания должны быть таковыми, чтобы учащийся не мог выполнить их, опираясь на уже имеющиеся знания, но достаточными для самостоятельного анализа проблемы и нахождения неизвестного.

Основными условиями использования проблемных ситуаций на уроке математики являются:

Со стороны учащихся:

• новая тема (“открытие” новых знаний);

• умение учащихся использовать ранее усвоенные знания и переносить их в новую ситуацию;

• умение определить область “незнания” в новой задаче;

• активная поисковая деятельность.

М.И. Махмутов считает, что большое значение при создании проблемной ситуации имеет то, как изложен новый материал. Разработаны два вида проблемного изложения нового материала.

Проблемная ситуация может создаваться, когда обнаруживается несоответствие имеющихся знаний и умений действительному положению вещей. Чтобы учащиеся обнаружили это несоответствие, учитель просит учеников вспомнить известную формулировку понятия, правила, а затем предлагает для анализа такие специально подобранные факты, при анализе которых возникает затруднение.

Второй вид проблемного изложения нового материала - проблемная ситуация создается, когда детям предлагается вопрос, требующий самостоятельного сопоставления ряда изученных фактов или явлений и высказывания собственных суждений и выводов, или дается специальное задание для самостоятельного решения. В процессе такого эвристического поиска возникает и поддерживается устойчивое внимание[21].

Опрос можно осуществить как решение учебно-познавательных задач, требующих не только воспроизведения изученного, но и установления более глубоких связей в понятии. Каждое из таких заданий требует не просто воспроизведения материала, а заставляет анализировать изученное, что способствует интеллектуальной активизации класса.

Постановка педагогом проблемных ситуаций ставит своей целью активизацию усилий учащихся по разрешению соответствующего противоречия. Проблемная ситуация может создаваться на всех этапах процесса обучения: при объяснении, закреплении, контроле (Приложение 2 Схема проблемной ситуации). В педагогической теории считается, что продуктивную познавательную деятельность учащегося в условиях проблемной ситуации и, соответственно, процесс проблемного обучения можно свести к следующим основным характерным этапам:

• возникновение (постановка) проблемной ситуации;

• осознание сущности затруднения (противоречия) и постановка проблемы (формулировка проблемной задачи);

• поиск способа решения проблемной задачи путем итерации догадок, гипотез и т.п. с попыткой соответствующего обоснования;

• доказательство гипотезы;

• проверка правильности решения проблемной задачи.

В проблемно-развивающем обучении акцент делается на общем развитии школьника, а не на трансляции готовых выводов науки учащимся[7].

Существуют различные приемы создания проблемной ситуации на уроках математики:

1.Одновременно предъявить противоречивые факты, теории или точки зрения.

2. Столкнуть разные мнения учеников вопросом или практическим заданием. Между житейским представлением учащихся и научным фактом.

3.1. Обнажить житейское представление учащихся вопросом или практическим заданием “на ошибку”.

3.2. Предъявить научный факт сообщением, экспериментом или наглядностью с затруднением. Между необходимостью и невозможностью выполнить задание учителя.

4. Дать практическое задание, невыполнимое вообще.

5. Дать практическое задание, несходное с предыдущими.

6.1. Дать невыполнимое практическое задание, сходное с предыдущими.

6.2. Доказать, что задание учениками не выполнено[13].

Проблемные ситуации могут быть различными по содержанию неизвестного, по уровню проблемы, по виду рассогласования информации, по другим методическим особенностям. Проблемные ситуации могут создаваться на всех этапах процесса обучения: при объяснении, закреплении, контроле. Учитель создает проблемную ситуацию, направляет учащихся на ее решение, организует поиск решения. Таким образом, ребенок становится в позицию субъекта своего обучения, и как результат, у него образуются новые знания, он овладевает новыми способами действия[37].

При использовании проблемных ситуаций на уроках математики в традиционной системе обучения у детей младшего школьного возраста можно развивать логическое мышление.

Используя проблемы развития математических способностей учащихся, психолог В.А. Крутецкий приводит типы задач для развития активного самостоятельного, логического мышления. Знание учителем этой типологии - важное условие создания проблемных ситуаций при изучении нового материала, повторении пройденного и при формировании умений и навыков. Вот некоторые из них: задачи с несформулированным вопросом; задачи с недостающими данными; задачи с излишними данными; задачи с несколькими решениями; задачи с меняющимся содержанием; задачи на соображение, логическое мышление[29].

Для организации урока математики в форме проблемного обучения, нами была подобранна примерная схема организации урока математики. (Приложение 3 Примерная схема организации урока математики с использованием проблемной ситуации). Данный схематический план организации проблемного урока (как и любой другой) динамичен в зависимости от учебной проблемы. Он выполняется полностью или отдельные пункты плана могут объединяться вместе.

Проблемное обучение позволяет эффективно сочетать как индивидуальную, так и групповую работу учащихся на уроке. В традиционном обучении групповая работа учащихся используется крайне редко. Между тем такая работа также является эффективным способом активного получения ими знаний, не говоря уже о воспитательном значении. В примерной схеме проблемного урока основное место занимает решение проблемы.

На этом этапе работа с учениками может выступать в виде:

• фронтальной работы со всем классом;

• групповой работы;

• индивидуальной работы.

На выбор того или иного вида работы влияет характер работ и учебные средства (комплекты учебных пособий и других материалов), время, имеющееся в распоряжении учителя.

Групповая работа предполагает деление класса на мини группы одинаковые по уровню развития. Количественный состав групп может быть различным.

Коллективная работа учащихся над решением какой-либо учебной проблемой никаким образом не исключает индивидуальной работы каждого из них, групповая работа по существу объединяет индивидуальную работу всех членов группы[12].

Обучая детей поиску выходов из проблемной ситуации, учитель формирует навык самостоятельного творческого подхода к любой трудности.

Задача анализа по дидактическим категориям состоит в том, чтобы выяснить:

• соответствует ли урок дидактическим принципам и требованиям к учебно-воспитательному процессу;

• соответствуют ли его ход и результаты требованиям к уроку и программе, основной дидактической цели;

• решены ли дидактические задачи и достигнута ли цель приращения в знаниях, умениях и навыках учащихся;

• какой была структура урока в целом и последовательность элементов внешней и внутренней структуры;

• соответствовало ли сочетание методов обучения, применение наглядности и ТСО дидактическим задачам урока, обеспечило ли это высокий уровень познавательной самостоятельности учащихся, соединение обучения и воспитания;

• чем характерны дифференциация и индивидуализация на данном уроке, в чем суть связи с жизнью[3].

Таким образом, нами были подобраны компоненты необходимые для анализа проблемной ситуации на уроках математики в начальной школе. (Приложение 4 Анализ деятельности учителя по созданию проблемной ситуации на уроке математики.)

Анализ имеющегося педагогического опыта использования технологии проблемного обучения для достижения предметных результатов по разделу нумерация на уроках математики в начальной школе

Применение технологии проблемного обучения на практике позволяет формировать у детей способности самостоятельно мыслить, добывать и применять знания в учебном процессе. Особенно эффективно применение технологии проблемного обучения или её элементов при изучении нового материала.

Анализируя педагогический опыт двух учителей начальных школ, можно выявить сходства и различия в использовании элементов проблемного обучения на уроках математики в начальной школе. Нами было проанализировано несколько статей педагогов начальных школ.

Обобщение педагогического опыта работы учителя начальных классов МБОУ «СОШ №10» Рузаевского муниципального района Дворецковой Татьяны Ивановны. При использовании ей технологии проблемного обучения дает такую возможность. Учащиеся самостоятельно открывают новые знания, а знания открытые детьми самостоятельно, запоминаются лучше, таким образом, нет необходимости дома зазубривать правила, которые детям не всегда понятны.

Секрет её работы: «Человек глубоко постигает лишь то, до чего додумывается сам». Все эти вопросы вполне решаемы, если процесс обучения строить на принципах развивающего обучения. Ни от случая к случаю, а систематически готовить уроки открытия новых знаний в соответствии с технологией проблемного обучения. В этом случае каждодневное объяснение учителем нового материала сменится поиском, решением возникших проблем, выходом из затруднительных ситуаций, самостоятельным выведением правил, свойств, алгоритмов и т.д.

В основе проблемных ситуаций “с затруднением” лежат противоречия, необходимость и невозможность выполнить задания учителя. Задание состоит из следующих приёмов:

• дается практическое невыполнимое задание;

• задание не схожее с предыдущими, т.е. такое с которыми ученики до настоящего момента не сталкивались.

Например: Урок математики во 2 классе.

При изучении темы “Умножение двузначного числа на однозначное” учитель подвела к постановке проблемы через задания устного счёта. Включила выражения на знание таблицы умножения, с которыми ученики справились без затруднений: 4 * 6, 20 * 3, 9 * 8, 10 * 6 и т. д. Последним было выражение 14 * 6, которое вызвало у детей затруднение. Возникла проблемная ситуация. Для вывода из неё учительница начала побуждающий диалог, который направлен на осознание затруднения и формулирование проблемы:

Учитель: Почему затрудняетесь в нахождении результата?

Дети: Мы такие ещё не решали.

Учитель: В чём затруднение?

Дети: Не умеем умножать двузначное число на однозначное.

Учитель: Кто догадался, какая задача стоит сегодня перед вами?

Дети: Научиться умножать двузначное число на однозначное.

Тема урока сформулирована. У всех появилась личная заинтересованность в усвоении нового, так как никто не знает, как найти результат этого выражения.

Конечно, приходится учитывать уровень подготовленности класса, социальный состав семей, ситуации на уроке, настроение, погоду. Постоянно находиться в поиске более удачных педагогических решений[22].

Из опыта учителя начальных классов Маларевой Ирины Константиновны специалиста государственного учреждения ЛНР «Луганское общеобразовательное учреждение-гимназия № 60 имени 200-летия г. Луганска».

При использовании побуждающего диалога она ставит цель: стимулировать учащихся к творческим действиям по осознанию противоречий и обозначению проблемы, по выдвижению и проверке гипотез. После окончания диалога она вместе с детьми делает вывод, потом учащиеся проверяют правильность своих выводов по учебнику. Снова ситуация успеха.

В её статье говорится: «На уроках математики использую проблемную ситуацию с затруднением. Сначала классу предлагается задание на пройденный материал, с которым ученики успешно справляются. В последнюю очередь – задание на новый материал, которое при отсутствии знаний, как правило, вызывает у детей затруднение. Далее проводится побуждающий диалог с целью осознания детьми противоречия. Диалог, как правило, начинаю с вопроса: «В чем затруднение?», «Почему получились разные ответы?», «Чем это задание не похоже на предыдущее?», «Какой возникает вопрос? Какая будет тема урока?» Тему записываю на доске, этап постановки проблемы завершается[9].

Для того чтобы сознательно использовать элементы проблемного обучения при изучении математики в начальных классах, важно, прежде всего, разобраться в возможных приемах создания проблемных ситуаций.

Проблемная ситуация действительно обозначилась, если у ребят появился эмоциональный отклик. Он возникает в определенный момент урока - при столкновении с вполне конкретным противоречием. По реакции детей все проблемные ситуации можно разделить на два типа: возникшие "с удивлением" и возникшие "с затруднением".

Таким образом, в разных регионах страны используют проблемные обучение, с использованием ситуаций с затруднением, но при этом могут использоваться разнообразные приёмы представления данной ситуации в зависимости от темы и индивидуальных особенностей класса.

Анализ учебно-методической литературы, опыта работы передовых учителей, а также учет содержания программы позволяют наметить наиболее характерные для практики обучения начальной математике приемы создания проблемных ситуаций. Формой реализации той или иной проблемной ситуации служат такие дидактические приемы, как постановка проблемного вопроса, проблемной задачи, практического задания.

В представленном педагогическом опыте, прослеживается использование таких дидактических приёмов, как: постановка проблемного вопроса, проблемной задачи.

В первом представленном примере использовался приём, столкновение учеников с новыми практическими условиями использования уже имеющихся знаний. Дети уже имеют знания таблицы умножения и знакомятся с новым практическим условием использования этого знания.

Также на уроках математики могут применяться и другие приемы работы, рассмотрим опыт использования данных приемов на уроках математики в начальной школе:

• Побуждение учащихся к проведению наблюдения, анализа, сопоставления, противопоставления с целью выявления общего и различного в наблюдаемых предметах и явлениях.

Учитель предлагает вниманию первоклассников плакат, на котором изображены несколько четырехугольников и пятиугольников. Все эти фигуры на плакате никак не сгруппированы, но четырехугольники окрашены в красный цвет, а пятиугольники – в зеленый. Учитель сообщает, что все красные фигуры можно назвать четырехугольниками, а зеленые – пятиугольниками. После этого перед классом ставится проблемный вопрос: «Как вы думаете, почему красные фигуры можно назвать четырехугольниками, а зеленые – пятиугольниками?».

Для решения данной проблемы дети должны провести ряд наблюдений, сопоставлений, сравнений. Они должны сравнивать мысленно термины «четырехугольник» и «пятиугольник». Анализируя эти слова, они должны, расчленить их, выделив в них знакомые им слова, являющиеся частями новых терминов, – «четыре» и «угол», «пять» и «угол». Такой анализ уже может направить их мысль в определенном направлении. Проверить правильность возникших предположений они смогут, обратившись к внимательному рассматриванию предложенных им фигур. Здесь снова придется провести ряд наблюдений, сопоставлений, сравнений, в результате которых они должны убедиться, что действительно все красные фигуры содержат по четыре угла, а зеленые – по пять углов. В итоге, дети должны прийти к выводу, который и будет ответом на поставленный проблемный вопрос[15].

• Использование задач с недостающими данными.

Чтобы решить задачу, нужно найти недостающие данные. Анализируя задачу, ученики устанавливают, какие данные необходимы для ее решения, и как их получить.

• Использование задач с лишними данными.

В проблеме, поставленной по задаче, должен быть элемент новизны, который возбуждает активность ученика и стимулирует его к поиску.

• Использование жизненных ситуаций, возникающих при самостоятельном выполнении учениками практических задач, и их анализ с целью формулировки проблемы.

Тема: Сравнение отрезков. Сантиметр.

Учащимся выдаются карточки, где на нелинованной бумаге начерчены отрезки.

Изображение отрезков с расположением концов на разных уровнях.

Узнайте, какой отрезок длиннее.

Концы отрезков находятся не на одном уровне. Возникает проблема для учащихся, как в этом конкретном случае сравнить отрезки по длине. Опираясь на приобретенные ранее знания, ученики могут предложить такой способ: измерить, например, ниткой длину одного отрезка, а потом приложить эту нитку к другому отрезку.

Чтобы показать, что не всегда можно пользоваться таким приемом, учитель предлагает измерить длину счетной палочки (карандаша) с помощью условной мерки и использовать в качестве мерки узкую полоску картона. Полоски разной величины. Измеряя, ученики приходят к выводу, что в одном случае мерка уложится два раза, в другом случае четыре раза, в третьем случае – три. Чему же все-таки равна длина счетной палочки (карандаша)? Учитель сообщает, что ученые-математики договорились измерять длину небольших предметов с помощью одной определенной мерки – сантиметра и демонстрирует модель сантиметра. С помощью модели ученики измеряют длину спички, полоски картона, которые заранее подготовил учитель.

• Постановка перед учениками таких практических задач, которые требуют поиска новых способов решения, новых подходов к решению знакомой задачи.

Например, урок математики на тему «Площадь фигуры», цель которого начать формирование у учащихся представления о площади фигуры и упражнять их в сравнении площадей фигур путем подсчета числа клеток, на которые разбиты фигуры. Начнем работу по ознакомлению с понятием площадь с изложения новых знаний.

Работа с учебником[27].

Какие фигуры изображены на рисунке? (Квадрат и круг.) Круг целиком поместился в квадрате, поэтому мы говорим, что площадь круга меньше площади квадрата.

Наложив далее вырезанный из бумаги треугольник на четырехугольник, мы видим, что треугольник целиком помещается в четырехугольнике. Площадь этого четырехугольника больше площади треугольника.

Далее учитель демонстрирует вырезанные из бумаги прямоугольники, которые полностью совпадают.

В таком случае мы говорим, что площади этих фигур равны.

Итак, мы привели только некоторые примеры основных приемов, используемых при обучении математике. Постоянное использование элементов проблемной ситуации приводит к тому, что ученик упражняется в постановке, поиске и решении различных задач на разном материале, приучается избирательно, строго целенаправленно применять имеющиеся у него знания. Но имеется ряд уроков, в содержании которых может и не найти себе места постановка проблемных вопросов, создание проблемной ситуации[14].

Анализ УМК «Школа России» и «Перспектива» с позиции выявления возможности применения технологии проблемного обучения для достижения предметных результатов по теме «Нумерация чисел» на уроках математики в начальной школе

УМК – совокупность всех учебно-методических документов (планов, программ, методик, учебных пособий и т.д.). В данном пункте нами рассмотрены два УМК, по которым работают школы города Камышлова. Это системы обучения УМК «Школа России» и УМК «Перспектива».

Примерная (типовая) учебная программа документ, который детально раскрывает обязательные (федеральные) компоненты содержания обучения и параметры качества усвоения учебного материала по конкретному предмету примерного (типового) учебного плана.

Анализ примерных рабочих программ, разработанных в соответствии с требованиями Федерального государственного образовательного стандарта, требований к результатам освоения основной общеобразовательной программы начального общего образования позволил сделать вывод, что реализация проблемного обучения на уроках математики является неотъемлемой частью каждого урока. Математическое содержание, представленное в примерной программе, по учебному предмету математика позволяет развить и организовать такие умения, как планирование этапов работы, определение последовательности учебных действий, осуществление контроля и оценки их правильности, поиск путей преодоления ошибок. В процессе обучения математике школьники учатся участвовать в современной деятельности[35].

Представленные элементы проблемного обучения в примерной программе по математике отражены и в найденной нами рабочей программе по учебному предмету «Математика». Это отраженно в задачах рабочей программы: формирование элементов самостоятельной интеллектуальной деятельности на основе овладения несложными математическими методами познания окружающего мира (умения устанавливать, описывать, моделировать и объяснять количественные и пространственные отношения)[36].

Таким образом, работа учителя на уроке математики должна строиться с учетом использования технологии проблемного обучения.

Общая сравнительная характеристика двух УМК представлена в приложении. (Приложение 5 Сравнительная характеристика УМК «Школа России» и УМК «Перспектива»).

Таким образом, программы двух УМК похожи между собой, но задания в УМК «Перспективе» более сложны и непонятны для понимания школьников в сравнении со УМК «Школой России», так как УМК «Перспектива» направлена на поиск ребенком материала. УМК «Перспектива» чрезвычайно близка к традиционной, трудность ее в том, что она предполагает помочь в становлении самостоятельности ребенка через поиск им материалов по новым темам. В учебниках УМК «Школы России» содержатся задания, которые под силу выполнить учащимся с низкими способностями, материал в них дается практически в готовом виде, время и силы на поиски его в дополнительных источниках тратить нет необходимости[43].

Обобщая вышесказанное, можно сделать вывод, что для использования проблемного обучения на уроках математики подойдут оба УМК.

Учебно-методический комплекс «Перспектива» больше направлен на самостоятельность учащихся. «Обучение не только математике, но и математикой» - ведущая идея линии УМК по математике, направленная на усиление общекультурного звучания математического образования и повышения его значимости для формирования личности ребенка. Содержание материала ориентировано на формирование у младших школьников умений наблюдать, сравнивать, обобщать, находить простейшие закономерности, что позволяет им освоить эвристические приемы рассуждения, их логику, развивает дивергентность мышления как важнейший компонент мыслительной деятельности, речевую культуру и позволяет расширить представления об окружающем мире средствами математики. Большое внимание уделяется развитию числовой грамотности учащихся, формированию вычислительных навыков на основе рациональных способов действий [41].

Поскольку прохождение преддипломной практики будет проходить на базе образовательного учреждения, реализующего УМК «Школа России» (научный руководитель кандидат педагогических наук А.А. Плешков), нами подробнее был проанализирован подробнее УМК «Школа России»: примерная программа и учебники по математике.

Анализ учебников «Математики», УМК «Школа России» (составители: М. И. Моро М.А. Бантова, Г.В. Бельтюкова), показывает, что проблемные методы используются, но отражаются частично.

Автор использует занимательные упражнения.

Игра «Кто первым получит 100?»

Двое играющих по очереди называют любое число от 1 до 10 и прибавляют его к сумме названных ранее чисел. Например, Маша называет 8, а Коля — 3 (сумма 11); Маша называет 5 (сумма стала 16), Коля называет 9 (сумма стала 25) и т. д. Выигрывает тот, кто первым получит 100.

Совет. Чтобы первым получить 100, надо первому получить 89, 79, 69. подумай почему.

Нестандартные задачи.

1. «Вот Вам 3 таблетки, - сказал доктор. Принимайте по одной через каждые 2 часа». Через сколько времени будет принята последняя таблетка?

2. Как за три взвешивания отвесить на чашечных весах 700 граммов крупы, если есть только одна гиря в 100 г?

Творческие упражнения по работе с задачами.

В одной теплице собрали 38 кг помидоров, в другой — 50 кг. Для продажи все эти помидоры разложили в ящики, по 8 кг в каждый. Сколько таких ящиков потребовалось?

Измени числа так, чтобы задача решалась двумя способами.

Сравни эти способы решения.

Однако следует отметить отсутствие разработанной технологии проблемного обучения при изучении нового материала. Анализ содержания учебного материала УМК «Школа России» показал, что не в полной мере обеспечивает реализацию принципа развивающего обучения, недостаточно количество проблемных заданий[4].

Остановимся на содержании учебного предмета в учебном процессе.

1 класс. На начальном этапе изучения нумерации осуществляется подготовительная работа к изучению чисел, в ходе которой младшие школьники учатся сравнивать и считать предметы, а также соотносить цифру и число предметов, устанавливать закономерности в расположении объектов. Вводятся проблемные ситуации типа: «Как сделать так, чтобы красных и синих треугольников стало поровну? Чтобы красных треугольников стало больше, чем синих? Синих меньше, чем красных?» (на рисунке к заданию один под другим изображены два ряда треугольников – 6 красных, 7 синих).

Помимо этого, задаются проблемные ситуации, где присутствуют элементы игры, например: «Это игра в домино. Какие числа пропущены?» (к заданию – иллюстрация цепочки домино, где пропущены некоторые числа). Учащиеся решают данные задания на основе уже имеющегося опыта.

В изучении чисел первого десятка часто присутствуют задания такого типа: «К какому числу прибавили 1, если получили 5? Какое число меньше: 5 или 3? 4 или 5?».

Далее, во втором полугодии, при изучении чисел второго десятка, имеют место следующие задания проблемного характера:

1) Прибавляй по одному, начиная с числа одиннадцать, до числа двадцать;

2) Отсчитывай по одному, начиная с числа двадцать до числа одиннадцать;

3) Назови число, следующее при счёте за числом двенадцать, идущее при счёте перед числом двадцать[23].

В процессе изучения темы «Числа от 1 до 100» на уроках математики во 2 классе младшие школьники учатся читать, записывать и сравнивать числа в пределах 100. Учащимся предлагаются задания, основанные на решении проблемных ситуаций, следующих типов:

1) Запиши число, в котором 2 десятка и 7 единиц; в котором 7 десятков и 2 единицы. Сколько всего единиц в каждом из этих чисел?

2) Спиши числа и объясни, что обозначает каждая цифра в их записи: 11, 14, 40, 44, 29, 90, 99.

3) Рассмотри, как получается каждое следующее число в ряду, продолжи его и прочитай числа:

100, 90, 80, 70, 60, *, *, *, *, *.

12, 23, 34, 45, *, *, *, *.

98, 88, 78, 68, *, *,* ,*.

4) Запиши 3 любых двузначных числа. Уменьши каждое из них на 10.

5) Какое число вычли из 37, если получили 7?

6) Один спортсмен прыгнул в высоту с шестом на 50 дм, а другой – на 52 дм. Поставь вопрос и реши задачу.

7) Из числа 40 вычесть сумму 8 и 2 (в ходе изучения темы «Числовые выражения»).

8) К разности чисел 54 и 20 прибавить 60.

9) Вычисли с объяснением. Проверь вычисления разными способами: 73+7, 80-7, 56+4, 90-9.

10) «Расшифруй». Чтобы узнать, какие цветы взяли для букета, поменяй местами карточки, на которых записаны выражения с равными значениями. Запиши буквы в полученном порядке (на иллюстрации к данному заданию изображены карточки с буквами в произвольном порядке). Для того, чтобы справиться с данной задачей, ученику необходимо, прежде всего, самостоятельно решить выражения, а затем расставить карточки в соответствии со значением[24].

В первом полугодии 3 класса продолжается изучение чисел в пределах 100, учебный материал во втором полугодии направлен на умение сравнивать трехзначные числа и записывать результат сравнения, упорядочивать заданные числа, заменять трехзначное число суммой разрядных слагаемых. В связи с этим применяются такие проблемные ситуации как:

1) Запиши число, в котором 3 сотни, 5 десятков и 7 единиц; в котором 3 сотни, 7 десятков и 5 единиц. Сколько всего единиц в каждом из этих чисел?

2) Запиши 5 любых трёхзначных числа. Уменьши каждое на 73.

3) Какое число вычли из 460, если получили 40?

4) Поставь скобки, чтобы равенство стало верным: 8×30-30:3×5=238.

5) Используя знаки действий и скобки, запиши:

число 24 четырьмя тройками или тремя двойками (24=33-3×3);

числа 20, 10, 810, 1008 четырьмя девятками;

число 1000 пятью девятками или шестью пятёрками[25].

В 4 классе продолжается изучение нумерации в пределах тысячи, со второй четверти вводятся многозначные числа. Некоторые учебные задания построены таким образом, что младшему школьнику требуется исследовать проблемные ситуации повышенного уровня сложности. Приведём примеры подобных заданий:

1) Сколько в числе 15400 всего десятков? Сотен? Тысяч? Сколько единиц в числе, содержащем 208 десятков? 32 сотни?

2) Реши ребус.

3) В магазин привезли 15200 тетрадей в пачках, по а штук в каждой, и 9500 блокнотов в пачках, по в штук в каждой. Объясни, что показывают выражения: 15200:а; 9500:в; 15200:а+9500:в.

4) Увеличь в 306 раз каждое из чисел: 58, 109, 231, 569[26].

Кроме того, в качестве проблемных ситуаций при изучении многозначных чисел авторы предлагают использовать уравнения.

Проведённый сравнительный анализ заданий в ходе изучения темы «Нумерация чисел» в комплектах учебников УМК «Школа России», УМК «Перспектива» позволяет сделать вывод о том, что проблемные ситуации, используемые во всех комплектах учебников, направлены на активизацию познавательной и мыслительной деятельности младших школьников. Ученики на уроках с элементами проблемного обучения чаще проявляют активность, находчивость, сообразительность и вместе с учителем добиваются высоких результатов[42].

Общая характеристика компонентов методической разработки

На сегодняшний день современное образование делает уклон на использование проблемного обучения, на то, чтобы учащиеся сами формулировали тему, цели и задачи уроков, самостоятельно ставили и решали проблемы.

Анализ методической литературы и педагогического опыта по реализации проблемного обучения на уроках математики позволяет сделать вывод: проблемное обучение является актуальным на данный момент и используется при обучении учащихся математике. В проанализированных опытах представлены конкретные проблемные ситуации, но не понятно, как они размещены в системе урока, как связаны с темой урока и для чего учитель применяет данные проблемные ситуации.

С учетом выбранных недостатков в ходе анализа различных методических продукций была определена форма организации деятельности, реализующая технологию проблемного обучения:

• конструкты по математике, вошедших в раздел «Нумерация чисел», учебника математики для 2 класс УМК «Школа России».

Подобранны проблемные ситуации, которые являются основной формой организации технологии проблемного обучения.

Цель создания проблемных ситуаций: развитие у учащихся:

1. умения видеть проблемные ситуации;

2. умения находить способы решения проблемных ситуаций;

3. развитие самостоятельной деятельности у учащихся;

4. умения самостоятельно ставить цели и находить тупи её достижения;

5. умения самостоятельно делать выводы, соотносить поставленные цели с достигнутыми результатами;

Конструкты уроков по математике с использованием проблемного обучения, представленные в работе:

• составлены для учащихся 2-х классов, обучающихся по УМК «Школа России»:

• объединены общей целью: доказательство результативности использования проблемной технологии, для достижения учащимися предметных результатов в предметной области математика;

• разработаны с учетом возрастных особенностей младшего школьного возраста, этапов урока открытия нового знания.

В дальнейшем подобранные и разработанные задания будут представлены в виде сборника, который будет адресован учителю и являться объектом для организации деятельности учащихся.

Структура сборника будет представлять собой совокупность его частей: титульный лист, аннотация (выходные данные, краткие сведения о самом сборнике); пояснительная записка с обоснованием необходимости использования проблемного обучения на уроках математики, представление самих конструктов уроков, список литературы.

На титульном листе будет отражаться наименование организации, название сборника и составитель данного сборника, также город и год.

В аннотации к сборнику будут представлены выходные данные, краткие сведения о самом сборнике, о том, что в него входит. Данный компонент необходим в сборнике для возможности предварительно в краткой форме познакомиться с содержанием сборника.

Пояснительная записка будет отражать цели и задачи сборника, необходимость использования проблемного обучения на уроках математики, актуальность создания сборника, объяснение объединения всех конструктов в единый сборник, краткое описание представленных конструктов.

Представление самих конструктов во взаимосвязи. Четыре конструкта для 2 класса, содержащие проблемные ситуации и связанные между собой. В конструкте отражены основные его компоненты, цели и задачи проведения именно этого урока, технологическая карта урока со всеми необходимыми этапами урока, прописанной деятельностью учителя и учащихся. Прописанными методами и планируемыми результатами, каждого этапа. Проблемная ситуация на каждом уроке должна использоваться на этапе постановки темы, цели и задач урока. Чтобы учащиеся получали информацию не в готовом виде, а добывали её самостоятельно.

Составление списка литературы к сборнику, это необходимо для доказательства научности используемых нами методов, форм и проблемных ситуаций на уроке.

Цель сборника конструктов с использованием проблемного обучения – доказать результативность использования проблемных ситуаций на уроке, улучшение предметных знаний учащихся.

Итак, разработанный методический продукт будет реализовываться во время преддипломной практики. (Приложение 6 Программа пробации сборника конструктов уроков по математике, с использованием проблемного обучения, направленных на формирование предметных результатов).

Обоснование способов оценки качества методической разработки, показателей успешности ее реализации

Оценка качества разработанного сборника конструктов уроков по математике с использованием проблемного обучения в начальной школе возможна на основе применения специально подобранных методов психолого-педагогической диагностики и диагностических методик.

Целью диагностической деятельности в процессе пробации является – оценка уровня применения технологии проблемного обучения на своей деятельности, проверка усвоения учащимися уровня математических знаний, отражающегося в предметных результатах по учебному предмету «Математика». Подобранные нами диагностики соответствуют обозначенной цели.

В процессе пробации предусмотрено комплексное применение разнообразных методов психолого-педагогической диагностики, которые позволят осуществить сбор разных типов данных об исследуемой характеристике (L, Q - данные).

«L-данные» - данные, полученные путём регистрации поведения человека в повседневной жизни и формализации оценок экспертов, которые наблюдают поведение испытуемых.

«Q –данные» - данные, полученные в процессе изучения личности с помощью личностных опросников, методов самооценок, самоотчётов, анкет, шкал самооценок состояний и т.д.

Для пробации эффективности сборника конструктов уроков математики с использованием проблемного обучения предлагается использовать метод экспертной оценки учителем МАОУ «Школа№1» КГО, имени Героя Советского Союза Бориса Самуиловича Семёнова (Приложение 7 Карта экспертной оценки).

Экспертная оценка – это метод поиска и результат применения метода, полученный на основании использования персонального мнения эксперта или коллективного мнения группы экспертов.

Под анализом экспертных оценок подразумевается, что эксперт заполняет индивидуально разработанный заказчиком формуляр, по результатам которого и производится всесторонний анализ проблемной ситуации, а также рассматриваются все возможные пути её решения. Эксперт выносит все свои соображения по данному вопросу в виде отдельного письменного документа.

В представленной карте отражены выбранные критерии оценки и шкала перевода баллов в уровень оценки. Для тщательного использования данного метода, необходимо осуществить подбор экспертов, их должно быть как минимум два для точной и объективной оценки[31].

Достоинства метода экспертных оценок:

1. Синтез опыта и интуиции для получения нового знания;

2. Возможность получения количественных оценок в случаях, когда отсутствуют статистические сведения или показатель имеет качественную природу;

3. Быстрота получения результатов.

Несмотря на достоинства, метод экспертных оценок имеет и недостатки: одним из основных недостатков является то, что достоверность и надёжность исследования в первую очередь зависят от компетентности специалистов, участвующих в опросе. Нет никаких гарантий, что полученные оценки в действительности достоверны. Существующие способы определения достоверности экспертных оценок основаны на предположении, что в случае согласованности мнений экспертов достоверность оценок гарантируется.

Для определения эффективности использования проблемного обучения необходимо использовать метод наблюдения. Для проверки уровня эффективности проблемного обучения на уроках математики нами предложена карта наблюдения за организацией проблемного обучения на уроках математики в начальной школе. (Приложение 8 Карта наблюдения)[32].

Под наблюдением принято понимать целенаправленное, планомерное и систематическое восприятие воспитательных явлений и процессов, направленное на вскрытие взаимосвязей и отношений в наблюдаемой действительности, которое имеет свои достоинства и недостатки.

Преимуществом метода наблюдения является то, что он непосредственно отражает действительность, максимально приближен к естественному ходу педагогических процессов, дает возможность наблюдать явления в те моменты, когда они проявляются, видеть среду в которой они существуют[31].

Таким образом, нами были предусмотри разнообразные способы оценки методической разработки, позволяющие отследить эффективность созданной разработки.

Подборка конструктов уроков по математике с использованием технологии проблемного обучения как средства достижения предметных результатов по теме «Нумерация чисел» на уроках математики в начальной школе

Тема: Умножение числа 2. Умножение на 2.

Класс: 2

Тип урока: открытие новых знаний.

Цель: (с позиции учащихся) – формирование знаний таблицы умножения и составление таблицы умножение на 2, пользуясь переместительным законом умножения, развивать навыки письменного и устного счета, мыслительной деятельности при решении задач и выражений[5].

Задачи: (с позиции учителя)	Планируемые результаты
Образовательные: формировать навыки составления таблицы умножения на 2;	Предметные: учащиеся научатся составлять таблицу числа 2 и таблицу умножения на 2: применять полученные знания при сравнении произведений и решении задач.
Развивающие формировать вместе с учителем цель урока, строить план действий, по реализации цели; формировать коммуникативные умения, способность выражать свои мысли с помощью построения речевых выражений; развивать математическую речь;	Метопредметные: регулятивные УУД: формулируют вместе с учителем цель урока, и план по реализации цели; Познавательные УУД: строят речевые выражения; Коммуникативные УУД: проявляют доброжелательное отношение друг другу. Применяют математические термины в устной речи;
Воспитательные: Воспитывать интерес к учебной деятельности;	Личностные УУД: формирование положительного отношения к учебно-познавательной деятельности.

Оборудование: плакат с таблицей умножения на 2.

Ход урока

Этап	Деятельность учителя	Деятельность учащегося	Методы, приемы, формы работы
Организационный момент.	Все ли готовы к уроку? - Что нужно для урока математики? - Сели девочки, сели мальчики	Да. Учебник, тетрадь, ручка, карандаш. Присаживаются.	Словесный метод(прием беседа) фронтальная форма.
Актуализация знаний	Каллиграфическая минутка 2 2 2 2 12 12 12 -Сколько раз по 2 надо взять, чтобы получилось число 12? Какой пример лишний? 36-5, 27 +4, 33 +3, 30+1, 26 + 5, 48 -17 -На какие две группы можно разбить эти выражения? Найди и исправь ошибки 18 – 9 = 7 (9) 9 + 6 = 15 13 – 6 = 8 (7) 7 + 6 = 13 15 – 8 = 9 (7) 16 – 9 = 7 5 + 7 = 12 11 – 2 = 8 (9) Замените, где можно данные выражения другим действием: 6+6+6 = 6 ▪3 у + у + у + у = у ▪ 4 3 +3+2+4 = 3 ▪ 2 +2+4 12 + 12 + 2 = 12 ▪ 2 +2 Закройте глаза (Я подписываю пример 4+5+6=) Что изменилось? Можно ли эти числа заменить умножением? Почему нельзя? Что же такое умножение? (устно) Царевна Несмеяна наплакала 2 ведра слёз по 5 литров каждое. Сколько всего литров слёз наплакала царевна? -Как вы узнали, сколько слёз наплакала царевна? А что больше 2 ▪ 5 или 2 ▪ 4? Почему?	Прописывают цифру 2 в тетради. 6 раз лишний 33, т.к. его значение равно 36, а в остальных 31 сумма и разность Находят ошибки. Заменяют действия. Числа стали разными, нельзя, потому что для умножения должны быть одинаковые слагаемые. сложение одинаковых слагаемых. 2+2+2+2+2=10 Взяли 2 литра по 5 раз. Больше 2*5, потому что мы берем 2 раза по 5.	Словестный метод (беседа) Практический метод (выполнения заданий) Наглядный метод (демонстрация заданий на доске) Фронтальная работа.
Сообщение темы урока.(создание и решение проблемной ситуации)	Таблица умножения. Достойна уважения. Она всегда во всем права. Чтоб ни случилось в мире, - А сколько ж будет дважды два Не знаете? По – прежнему четыре. 2+2 2+2+2 2+2+2+2 2+2+2+2+2 2+2+2+2+2+2 -Что заметили? -Сколько раз число 2 взяли в первом случае? -Как записать это умножением? Что мы с вами сейчас записали, это что? С помощью какого свойства мы преобразовали данные выражения? Какие цели мы можем поставить на урок?	Число 2 взяли сначала по 2, потом по 3, по 4, по 5. 2*2 2*3 2*4 2*5 Таблица умножения на 2. С помощью переместительного свойства. Узнать таблицу умножения на 2.	Словесный метод (беседа, объяснение) Практический (преобразование выражений) Наглядный (демонстрация заданий) Фронтальная работа.
Открытие новых знаний.	Первый множитель 2 умножить на второй множитель 3, значение произведения равно 6. 2 ▪ 1 = 2 2 ▪ 2 = 4 2 ▪ 3 = 6 2 ▪ 4 = 8 2 ▪ 5 = 10 2 ▪ 6 = 12 2 ▪ 7 = 14 2 ▪ 8 = 16 2 ▪ 9 = 18 2 ▪ 10 = 20 Как называются числа при умножении? Рассмотрите выражения: 3 ▪ 2 = 6 4 ▪ 2 = 8 -Как найти значение данных произведений? -Выполните перестановку множителей и найдите значение произведения. - Давайте научимся читать таблицу умножения Физкультминутка (под музыку песни «Дважды два»)	Проговаривают каждый пример, заполняя таблицу. Слагаемые применить переместительный закон умножения дважды два четыре и т.д.	Словесный (беседа, объяснение) Наглядный (демонстрация заданий в учебнике и на карточке) Практический (выполнение заданий) Фронтальная работа.
Первичное закрепление	- Сколько лапок у 3 гусят? ( 6 ) - Сколько лапок у 2 котят? ( 8 ) - Сколько крыльев у 4 щенят? ( 0 ) решение примеров с. 68 № 1 на доске по цепочке. -работа в парах с. 68 № 2. Проверка. -решение задачи № 3 самостоятельно после предварительного разбора и выполнения схематического рисунка.	Выполняют задания по учебнику.	Словесный (беседа) Наглядный (демонстрация заданий в учебнике) Практический (выполнение практических упражнений) Фронтальная работа.
Подведение итогов	Что нового узнали? -Где в дальнейшем пригодятся знания, полученные сегодня? - Кто понял материал? -Кто не совсем понял? -Как вы думаете, кто лучше всех занимался сегодня на уроке? -Что было решать легко? - Кто хочет рассказать таблицу по памяти?	Узнали таблицу умножение на 2. Отвечают на вопросы.	Словесный (беседа) Фронтальная работа.
Домашнее задание	Выучить таблицу наизусть. Чтобы убедиться, что материал вами усвоен, предлагаю «блиц-опрос»	Записывают домашнее задание, задают вопросы, если есть.	Словестный (беседа)

Тема. Умножение. Закрепление изученного.

Тип урока: урок повторения и закрепления.

Цель. Структурировать знания учащихся о действии умножения, умение решать текстовые задачи на нахождения произведения, совершенствовать вычислительные навыки; развивать внимание, логическое мышление; способствовать воспитанию познавательного интереса к математике[40].

Задачи: (с позиции учителя)	Планируемые результаты
Образовательные: повторить таблицу умножения на 2, структурировать навыки по составлению таблицы умножения;	Предметные: Самостоятельно без подсказку воспроизводят таблицу умножения на 2;
Развивающие формировать вместе с учителем цель урока, выявлять места затруднений, строить план действий по реализации выявленных затруднений; формировать навыки сравнения полученных знаний с ранее имеющимися; формировать коммуникативные умения, способность выражать свои мысли с помощью построения речевых выражений; развивать математическую речь;	Метапредметные: регулятивные УУД: формулируют вместе с учителем цель урока, выявляют затруднения, строят план действий по выявлению затруднений, проводить сравнительный анализ приобретенных знаний; Познавательные УУД: строят речевые выражения; Коммуникативные УУД: проявляют доброжелательное отношение друг другу. Применяют математические термины в устной речи;
Воспитательные: Воспитывать интерес к учебной деятельности;	Личностные УУД: формирование положительного отношения к учебно-познавательной деятельности.

Материалы и оборудование: учебник, книжка «Помощница», индивидуальные карточки, таблицы для устного счёта, таблицы по теме «Умножение», аудиозапись «Танцуем сидя».

Ход урока

Этап	Деятельность учителя	Деятельность учащихся	Методы, приемы, формы работы
Организационный момент	Математику, друзья, Не любить никак нельзя. Очень строгая наука, Очень точная наука, Интересная наука- Это математика!	Приветствуют учителя, присаживаются.	Словесный (беседа) фронтальная форма
Актуализация знаний	Сегодня, милые ребятки, Цифра спряталась в загадке: Есть, друзья, такая птица, Если сядет на страницу, Очень рад бываю я, А со мною вся семья - Из каких элементов состоит цифра 5? Опишите последовательность написания цифры 5. - Запишите цифру 5. - Если мы запишем цифру 5 два раза, какое число получим? - Охарактеризуйте числа 5,55 На доске таблица карты «Хоттабыча». Определите последовательность чисел. – Какие числа спрятались? – Докажите правильность своего ответа. Чтобы попасть в страну математики Хоттабыч предлагает назвать примеры, которые едут в вагонах: в 1 вагоне едут примеры с ответом 18, во 2 вагоне с ответом 23 , в 3 вагоне 32. - Какие примеры едут в вагонах?	Отгадка: цифра 5. На доске карточка с цифрой 5 Записывают цифру 5. число 5-однозначное,нечётное,число 55-двухначное, нечётное, в нём 5 единиц и пять десятков. Составление примеров по рядам.	Словесный (беседа, объяснение) Наглядный (демонстрация зданий) Практический (выполнение заданий) фронтальная работа.
Самоопределение к деятельности. (проблемное обучение)	Для того чтобы узнать над чем мы будем работать на уроке, я предлагаю вам выполнить поисковую работу (на доске примеры). Игра «Перевёртыши» Решить зашифрованные примеры. Расположить числа-ответы в возрастающем порядке и прочитать тему. (У) 93-90= (М)81-64= (ж) 9+77= (е) 72+22= (н)56-34= (о) 76-11= (н)88+8= (е)91+9= (и)99-2= Прочтём название темы урока: «Умножение». - Сегодня мы с вами повторим и закрепим знания о действии умножения.	Решают примеры, располагают их в порядке возрастания, составляют тему урока. (У) 93-90=3 (М)81-64=27 (н)56-34=32 (о) 76-11=65 (ж) 9+77=86 (е) 72+22=94 (н)88+8=96 (и)99-2=97 (е)91+9=100 Умножение	Словесный (беседа, объяснение) Наглядный (демонстрация зданий) Практический (выполнение заданий) фронтальная работа.
Работа по теме урока	Что такое умножение? -Назовите знак умножения? - Что обозначает первое число в записи умножения? - Что обозначает второе число в записи умножения ? - Как называются числа при умножении? - Как называется результат умножения? - Назовите приемы умножения числа на 1, на 0. Работа по учебнику, страница 63 а) Задание 1 (устно). Заменить сложение действием умножение б) Задание 2 (по вариантам). Самостоятельная работа. Заменить сложение умножением, умножить на 1 и 0. Проверка: фронтальная в) Индивидуальная работа у доски по карточкам. 16∙1 29∙0 1∙52 1∙70 15∙1 0∙33 0∙17 1∙42 61∙1 Физкультминутка Аудиозапись «Танцуем сидя»	Арифметическое действие-сложение одинаковых слагаемых * Какое число взято Сколько раз берём это число Множители Произведение Вывешиваются таблицы Выполняют задания по учебнику.	Словесный (беседа, объяснение) Наглядный (демонстрация зданий) Практический (выполнение заданий) фронтальная работа.
Закрепление изученного	а) Устное решение задач Десять солдат шли на парад, Ярко погоны на солнце горят. Сколько погонов шло на парад? 2∙10=20 (погонов) На окне Герды в двух горшках появилась по 6 бутонов роз. Сколько всего роз распустится? 6∙2=12 (бутонов) Незнайка сочинил о своих друзьях стихи в каждом стихотворении 4 строки , а друзей 5. Сколько строк сочинил Незнайка? 4∙5=20 (строк) Беседа о героях книг Г.Х.Андерсена, Н.Н. Носова б) Проверка домашнего задания: задача 8 (1), страница 6 Анализ составленной задачи по рисунку. в) Составление и решение задачи 8(2), стр. 6. Коллективное составление задачи по рисунку. Схематическое выполнение краткой записи. Самостоятельная решение задачи. Какое свойство умножения вы знаете? -Задание: решить выражение, используя переместительное свойство 3∙6=18 32∙2=34 10∙5=50 6∙3= 1∙34= 5∙10= .Математический диктант 4 взять 3 раза; Первый множитель 8, второй 2 найти произведение; Заменить сложение умножение 6+6+6+6; Заменить умножение сложение 8∙2; 1 умножить на 42; 63 умножить на 1; 0 умножить 8; 16 умножить на 0 Взаимопроверка. Работа эксперта.	Решают задачи устно. Ответы детей. Если затрудняются ответить, то пользуются «Помощницей».	Словесный (беседа) Практический (выполнение заданий) Наглядный (демонстрация заданий в учебнике)
Подведение итогов	Оцените свою работу на уроке Над каким арифметическим действием мы сегодня работали? - Всё ли вам было понятно? - Какое задание показалось трудным? - Кому нужна помощь?	работа со смайликом ответы детей	Словесный (беседа) Фронтальная работа

Итак, мы осуществили подборку конструктов уроков по математике с использованием технологии проблемного обучения как средства достижения предметных результатов по теме «Нумерация чисел» на уроках математики в начальной школе.

Список литературы

1. А.Л. Челин. О книге «Математический взгляд на актуальные проблемы методики обучения математике в начальной школе». URL: https://avidreaders.ru/book/matematicheskiy-vzglyad-na-aktualnye-problemy-metodiki.html (дата обращение 15.01.2020)

2. Амонашвили Ш.А. Гуманная педагогика. Актуальные вопросы обучению родному языку и развития личности. // Издательство «Амрита» 2011г. (дата обращения 14.12.2019)

3. Анализ урока с использованием проблемности в обучении URL: .https://studwood.ru/1921940/pedagogika/analiz_uroka_ispolzovaniem_problemnosti_obuchenii (дата обращения 26.01.2020)

4. Анализ учебников математики с точки зрения реализации проблемного обучения. URL: https://infourok.ru/analiz-uchebnikov-matematiki-s-tochki-zreniya-realizacii-problemnogo-obucheniya-3450206.html (дата обращения 08.02.2020)

5. Барташевич Н.В. Умножение числа 2. Умножение на 2. (УМК Школа России 2 класс).. URL: https://nsportal.ru/nachalnaya-shkola/matematika/2012/04/19/umnozhenie-chisla-2-umnozhenie-na-2-umk-shkola-rossii-2 (дата обращения 22.03.2020)

6. Брызгалова С.И. Проблемное обучение в начальной школе: Учеб. пособие / С. И. Брызгалова, Калининград: КГУ, 1998. 90с. (дата обращения 28.11.2019)

7. Буториной Г.Г. Проблемное обучение на уроках математики. (дата обращения 10.12.2019)

8. В.Т.Кудрявцев. О различиях систем развивающего обучения Д.Б. Эльконина – В.В. Давыдова и Л.В. Занкова (дата обращения 13.01.2020)

9. Вялова И.А. Проблемное обучение на уроках математики МОУ «СОШ №1 с УИОП г. Шебекино Белгородской области 2009г.(дата обращения 16.01.2020)

10. Данилов Д.Д., Исаева Н.А. Резервы повышения эффективности обучения на основе моделирования проблемных ситуаций // Начальная школа плюс До и После. 2014. №04. - С. 22-34 (дата обращения 20.02.2020)

11. Дворецковой Т.И. Обобщение педагогического опыта работы учителя начальных классов МБОУ «СОШ №10» Рузаевского муниципального района URL: https://infourok.ru/obobschenie-opita-raboti-uchitelya-nachalnih-klassov-po-probleme-tehnologiya-problemnodialogicheskogo-obucheniya-na-urokah-v-nac-1231132.html (дата обращения 17.12.2019)

12. Зейб Е.В. Методическое пособие для учителей начальных классов «Общие пути и способы создания проблемных ситуаций на уроках математики в начальной школе» URL: https://multiurok.ru/files/mietodichieskoie-posobiie-dlia-uchitieliei-nachal-nykh-klassov-obshchiie-puti-i-sposoby-sozdaniia-probliemnykh-situatsii-na-urokakh-matiematiki-v-nachal-noi-shkolie.html (дата обращения 16.01.2020)

13. Использование проблемных ситуаций на уроках математики как средство формирования предметных и метапредметных умений младших школьников URL: https://infourok.ru/statya-ispolzovanie-problemnih-situaciy-na-urokah-matematiki-kak-sredstvo-formirovaniya-predmetnih-i-metapredmetnih-umeniy-mlads-3962400.html (дата обращения 8.12.2019)

14. Капилина М.В. Использование элементов проблемного обучения на уроках математики в начальной школе. URL: http://www.erono.ru/art/?ELEMENT_ID=1066 (дата обращения 26.01.2020)

15. Карелина Т.М. Методы проблемного обучения // Математика в школе. – 2010. - № 5. – с.31. (дата обращения 26.01.2020)

16. Ковалева Г. Я. Использование технологии проблемного обучения на уроках в начальных классах // Учительский журнал. - 2009. - N 4. - С. 32-37 (дата обращения 26.01.2020)

17. Кудрявцев В.Т. Проблемное обучение: истоки, сущность, перспективы. - М.: Знание, 2004. - 180 с. (дата обращения 28.11.2019)

18. Лернер И.Я. Проблемное обучение. - М.: Знание, 1974. - 64 с.(дата обращения 28.11.2019)

19. Матюшкин А.Н. Проблемные ситуации в мышлении и обучении. – М. : Просвещение, 1977 (дата обращения 8.12.2019)

20. Махмутов М. И. Теория и практика проблемного обучения. - Казань: Таткнигоиздат, 1972. - 365 с. (дата обращения 26.01.2020)

21. Махмутов М.И. Организация проблемного обучения в школе. - М.: Педагогика, 1987. - 156 с. (дата обращения 26.01.2020)

22. Махмутов М.И. Проблемное обучение. М., 1975. (дата обращения 28.11.2019)

23. Моро Волкова Степанова Учебник Математика 1 класс часть 1,2. (дата обращения 26.01.2020)

24. Моро Волкова Степанова Учебник Математика 2 класс часть 1,2. (дата обращения 26.01.2020)

25. Моро Волкова Степанова Учебник Математика 3 класс часть 1,2. (дата обращения 26.01. 2020)

26. Моро Волкова Степанова Учебник Математика 4 класс часть 1,2. (дата обращения 26.01.2020)

27. Моро М.И. и др Учебник. Математика. 3 класс. 2 ч..2012 г (дата обращения 26.01.2020)

28. Н.А. Каштанова. Проблемное обучение на уроках математики, как средство развития младших школьников. Саранск 2016.(дата обращения 15.01.2020)

29. Николау Л.Л. Технология проблемного обучения математике в начальных классах. URL: http://www.dslib.net/teoria-vospitania/tehnologija-problemnogo-obuchenija-matematike-v-nachalnyh-klassah.html (дата обращения 15.12.2019)

30. Оконь В.В. Основы проблемного обучения. - М.: Просвящение, 1986. - 208 с. (дата обращения 10.12.2019)

31. Основы исследовательской деятельности педагога. Л.Д. Устьянцева. Екатеринбург 2009 (дата обращения 15.03.2020)

32. Оценка работы учащихся в проблемном обучении. URL: https://lektsia.com/7x9f21.html. (дата обращения 16.02.2020)

33. Пенязь И.Г. Проблемное обучение. Концепция проблемного обучения получила широкое распространение, тем не менее, существует несколько подходов к ее трактовке. URL: https://nsportal.ru/nachalnaya-shkola/vospitatelnayrabota/2014/10/09/problemnoe-obuchenie-kontseptsiya-problemnogo (дата обращения 24.11.2019)

34. Плотникова Г.М. Проблемное обучение на уроках математики. URL: https://urok.1sept.ru/%D1%81%D1%82%D0%B0%D1%82%D1%8C%D0%B8/630175/ (дата обращения 08.02.2020)

35. Примерная программа по математике УМК «Школа России» (дата обращения 29.02.2020)

36. Рабочая программа по предмету "Математика" УМК "Школа России". URL: https://infourok.ru/rabochaya-programma-po-predmetu-matematika-umk-shkola-rossii-1714171.html (дата обращения 29.02.2020)

37. Савченко А.Я. Дидактика начальной школы. – Киев, 1997. (дата обращения 20.11.2019)

38. Селевко Г.К. проблемное обучение/ Г.К. Селевко // Школьные технологии.-2006.-№2.-с.61-66. (дата обращения: 20.11.2019)

39. Сущность проблемного обучения. URL: https://studopedia.ru/11_56147_sushchnost-problemnogo-obucheniya.html (дата обращения 5.12.2019)

40. Урок математики во 2 классе по теме "Умножение. Закрепление". URL: https://infourok.ru/urok-matematiki-vo-klasse-po-teme-umnozhenie-zakreplenie-1682102.html (дата обращения 22.03.2020)

41. Учебно-методический комплекс «Перспектива». Под редакцией Л.Ф. Климановой. URL: https://megaobuchalka.ru/9/33943.html (дата обращения 08.02.2020)

42. Фатова И.А. Анализ программ и учебников по математике в начальной школе с точки зрения использования проблемных ситуаций при обучении нумерации чисел. URL: https://nsportal.ru/nachalnaya-shkola/matematika/2017/07/13/analiz-programm-i-uchebnikov-po-matematike-v-nachalnoy. (дата обращения 8.02.2020)

43. Федеральный государственный образовательный стандарт начального общего образования / Министерство образования и науки Российской Федерации.-М.: Просвещение,2015г.;(дата обращения 15.11.2019)

44. Федорова О.М. Современные УМК: сравнительный анализ в контексте требований ФГОС URL: https://multiurok.ru/files/sovriemiennyie-umk-sravnitiel-nyi-analiz-v-kontiek.html (дата обращения 03.02.2020)

Приложение 1

Сравнительная характеристика проблемного и традиционного обучения

Традиционное	Проблемное
1. Материал дается в готовом виде, учитель обращает внимание прежде всего на программу.	1. Новую информацию учащиеся получают в ходе решения теоретических и практических задач.
2.Цель сложившегося типа обучения: усвоение результатов научного познания, вооружения учащихся знанием основ наук, привития им соответствующих знаний и навыков.	2.Цель проблемного обучения более широкая: усвоение не только результатов научного познания, но и самого пути, процесса получения этих результатов, она включает еще и формирование познавательной деятельности ученика, и развитие его творческих способностей (помимо овладения системой знаний, умений и навыков). Здесь акцент делается на развитие мышления.
3. В устной подаче или через учебник возникают проблемы, преграды и трудности вызванные временным выключением учащегося из дидактического процесса.	3. В ходе решения проблемы учащийся преодолевает все трудности, его активность и самостоятельность достигает здесь высокого уровня.
4. Темп передачи информации ориентирован на более сильных, средних или слабых учащихся.	4. Темп передачи сведений зависит от учащегося или группы учащихся.
5. Контроль школьных достижений только частично связан с процессом обучения; он не является его органической частью.	5. Повышенная активность учащихся способствует развитию позитивных мотивов и уменьшает необходимость формальной проверки результатов.
6. Отсутствует возможность обеспечения всем учащимся стопроцентных результатов; наибольшую трудность представляет применение информатизации в практике.	6. Результаты преподавания относительно высокие и устойчивые. Учащиеся легче применяют полученные знания в новых ситуациях и одновременно развивают свои умения и творческие способности.
7.Принцип передачи слушателям готовых выводов науки учащимся.	7. Принцип поисковой учебно-познавательной деятельности ученика (основанной на закономерности проблемности усвоения знаний), то есть открытия или выводов науки, способов действия, «изобретения» новых предметов или способов приложения знаний к практике и «художественного отображения действительности».

Приложение 2

Схема проблемной ситуации

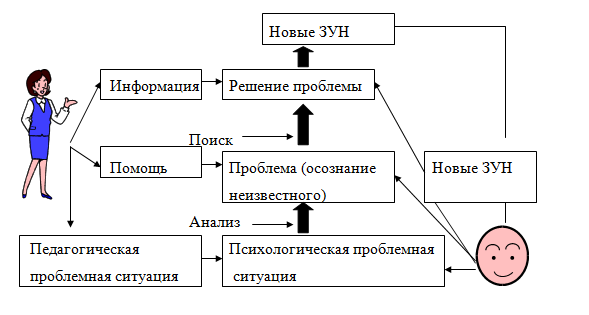
Приложение 3

Примерная схема организации урока математики с использованием проблемной ситуации

1.Создание учебной проблемной ситуации (реальной или формальной) с целью возбудить у учащихся интерес к данной учебной теме и мотивировать целесообразность ее рассмотрения.

2.Постановка познавательной задачи (или задач), возникающей в данной проблемной ситуации, четкая ее формулировка.

3.Изучение различных условий, характеризующих поставленную проблему, обсуждение возможностей моделирования ее условия или замена этой модели более простой и наглядной. Выдвижение гипотезы.

4.Процесс решения поставленной задачи (обсуждение задачи в деталях, выявление существенного и несущественного, ориентация в возможных трудностях при ее решении, соотношение данной задачи к имеющимся знаниям.)

5.Исследование получаемого решения задачи, обсуждение его и выявление новых знаний.

6. Применение нового знания посредством решения специально подобранных задач для его усвоения.

7.Обсуждение возможных расширений и обобщений результатов решения в рамках исходной проблемной ситуации.

8.Изучение полученного решения задачи и поиск других более экономных, более изящных способов ее решения.

9.Подведение итогов проделанной работы, выявление существенных моментов в содержании, способах решения, результатах, обсуждениях, выявление перспектив применения новых знаний и опыта.

Приложение 4

Анализ деятельности учителя по созданию проблемной ситуации на уроке математики

1. формирование новых, понятий и способов действия - достаточно ли времени на самостоятельную работу учащихся, все ли понятия получили полное освещение в объяснении учителя; была ли связь нового с ранее изученным, кто из учащихся и насколько продвинулся вперед, кто слабо усвоил материал и нуждается в помощи на следующем уроке; какие понятия и способы действия учащиеся получили в готовом виде (в виде образца) и какие раскрыли самостоятельно и т.д.;

2. формирование умений и навыков - качество самостоятельных работ учащихся, какие умения и навыки более всего применялись, какие и у кого имелись успехи, неудачи, готовы ли учащиеся к выполнению домашнего задания и т.д.;

3. постраннее работы с теми учащимися, которые плохо усвоили новый материл, или не усвоили совсем.

Приложение 5

Сравнительная таблица УМК «Школа России» и «Перспектива»

Критерии для сравнения	УМК «Перспектива»	УМК «Школа России»
Общая характеристика	УМК «Перспектива» полностью отвечает требованиям ФГОС НОО. Автор проекта – Л.Г.Петерсон.	Руководитель данного УМК – кандидат педагогических наук А.А.Плешаков на данный момент это один из используемых комплексов для 1-4 классов. Данное УМК соответствует требованиям ФГОС НОО.
Основное содержание	В основу программы положен деятельностный подход, который объединяет развивающий и классический подходы через развитие учения решать задачи, ставить цели, нести ответственность за результат.	Эта программа предполагает подход проблемно-поисковый: создается проблема, находятся доказательства, формулируется вывод, результаты сравниваются с эталоном, выдвигаются предположения. Это должно вызвать у ребенка желание учиться.
Основная идея программы	Программа направлена на то, чтобы научить школьника самостоятельно находить новые знания. Лозунг педагога, работающего по этой программе: «Услышал – забыл, увидел – запомнил, выполнил – усвоил!»	Программа направлена на максимальное духовно-нравственное развитие учащегося. Создатели УМК говорят о необходимости развития чувства патриотизма, об уважении своего народа, других народов России, их языка, культуры, традиций и обычаев, символики. Так как ребенок должен быть цельной личностью, то и воспитание, и обучение должны иметь равное значение.
Типические свойства программы	Можно выделить такие свойства программы. Комплектность – она состоит в формировании умения работать с учебником, справочником и другим оборудованием. Инструментальность подразумевает обучение умению пользоваться словарями, справочниками, методическими пособиями. Интерактивность – наличие в учебниках и учебных пособиях интернет-адресов. Интеграция – это свойство, которое выражается в том, что в учебных курсах грамотно сочетаются понятия из разных областей.	Перечислим основные свойства программы. Главным является воспитание. Характер обучения – личностно-ориентированный, деятельностный. Умелое сочетание инновационного подхода с традиционным. Если ребенок имеет средние, ничем не выдающиеся способности, то эта программа для него. Кроме того, учитываются возрастные особенности школьника, а материал учебников понятный и доступный для родителей и детей.
Особенности УМК	Имеется не только учебник, но хрестоматия и рабочая тетрадь для работы школьника дома.	Яркие, хорошо и интересно иллюстрированные учебники, удобный для чтения шрифт.
Основные положения и принципы УМК	Основополагающими принципами комплекта являются: гуманистический принцип принцип историзма коммуникативный принцип принцип творческой активности. Обучение строится по диалектическому принципу, когда введение новых понятий и идей, первоначально представленных в наглядно-образной форме или в виде проблемной ситуации, предшествует их последующему детальному изучению. Каждый учебник снабжен системой заданий, направленных на развитие как логического, так и образного мышления ребенка, его воображения, интуиции. В учебниках системно выстроен теоретический материал, к которому предложены практические, исследовательские и творческие задания, позволяющие активизировать деятельность ребенка, применять полученные знания в практической деятельности, создавать условия для реализации творческого потенциала ученика.	Обобщающими характеристиками содержания комплекта являются следующие: - Личностно-развивающий характер образования с приоритетом духовно-нравственного развития ребенка. - Граждански-ориентированный характер образования, предусматривающий воспитание ребенка гражданином своей страны, развивающий чувства гражданственности и патриотизма. - Глобально-ориентированный характер образования, отвечающий новым задачам образования в эпоху глобализации. - Экоадекватный характер образования с приоритетным вниманием к проблемам экологической этики, воспитанию любви и бережного отношения к природе. Основополагающие принципы УМК «Школа России»: • принцип воспитания гражданина России; • принцип ценностных ориентиров; • принцип экоадекватного характера образования; • принцип обучения в деятельности; • принцип работы на результат; • принцип синтеза традиций и инноваций; • принцип глобальной ориентации образования;ч • принцип вариативности.
Отличительные черты	Методической основой системы учебников «Перспектива» является методический инструментарий завершенных предметных линии учебников и специально разработанная система информационно-образовательных ресурсов. Преимущество обучения по УМК «Перспектива» в том, что, система построения учебного материала позволяет каждому ученику поддерживать и развивать интерес к открытию и изучению нового. В учебниках задания предлагаются в такой форме, чтобы познавательная активность, познавательный интерес и любознательность ребенка переросли в потребность изучать новое, самостоятельно учиться. Ученик на каждом уроке, как бы, приоткрывает для себя содержание будущих тем. Следующая особенность УМК «Перспектива» в контексте его соответствия требованиям ФГОС - это большие возможности для решения воспитательных задач. Реализация в УМК Концепции духовно-нравственного развития и воспитания личности гражданина России направлена на формирование ценностного мировоззрения, воспитание и становление нравственной позиции личности младшего школьника. Эти задачи педагог решает в процессе обсуждения системы вопросов, проблемных и практических ситуаций, текстов, направленных на воспитание самых добрых чувств, любви и интереса к своей семье, малой и большой Родине, традициям и обычаям народов, проживающих на территории России, их культурному и историческому наследию. Еще одной отличительной чертой системы учебников «Перспектива», обеспечивающей ему статус ядра информационно-образовательной среды для начальной школы, является разработанная специальная система навигации, позволяющая ученику ориентироваться как внутри УМК, так и выходить за его рамки в поисках других источников информации. Для УМК «Перспектива» разработано новое методическое сопровождение - «Технологические карты», помогающие учителю реализовывать требования ФГОС в образовательном процессе. «Технологические карты» - это новый методический инструментарий, обеспечивающий учителю качественное преподавание нового учебного курса путем перехода от планирования урока к проектированию изучения темы. В «Технологических картах» определены задачи, планируемые результаты (личностные и метапредметные), указаны возможные межпредметные связи, предложен алгоритм прохождения темы и диагностические работы (промежуточные и итоговые) для определения уровня освоения темы учащимися.	Основной особенностью методов и форм является то, что предпочтение отдается проблемно-поисковой и творческой деятельности младших школьников. Проблемно-поисковый подход дает возможность применять обширный арсенал методов и приемов эвристического характера, целенаправленно развивая познавательную активность и самостоятельность учащихся. Важной особенностью учебников является выделение в них базового и повышенного уровней учебного материала, позволяющего ученикам продвигаться в освоении учебных курсов с учетом индивидуальных особенностей, интересов и склонностей. Особенности, которые позволят ребенку успешно учиться по данной программе: никаких особых качеств от ребенка не требуется.

Приложение 6

Программа пробации сборника конструктов уроков по математике с использованием проблемного обучения, направленных на формирование предметных результатов.

Тема: сборник конструктов уроков по математике с использованием проблемного обучения.

Актуальность регламентируется требованиями Федерального Образовательного Стандарта Начального Общего Образования, требующим использовать в организации урока системно-деятельностный подход, который создает усвоение обучающимися новых знаний, умений, компетенций, видов и способов деятельности.

Объект проектирования: процесс проблемного обучения младших школьников на уроках математики.

Форма проектирования: сборник конструктов уроков с элементами проблемного обучения, направленных на достижение предметных результатов по математике.

Цель: доказать результативность использования проблемного обучения на уроках математики для достижения предметных результатов в области математики.

Задачи:

1. разработать программы пробации, выбор и обоснование диагностического инструментария;

2. разработка и проведение системы конструктов по математике с использованием проблемного обучения;

3. оценить работу учащихся по предложенной карте наблюдения, выявить уровень усвоения учащимися новых знаний;

4. оценить предметные результаты до проведения системы уроков математики с проблемным обучением и после. Выявить динамику.

Диагностический инструментарий - разработанная карта наблюдения.

Критерии оценки ожидаемых результатов.

Увеличения предметных результатов по математике у учащихся. Умение видеть проблемные ситуации и самостоятельно решать или предлагать способы решения предложенных проблемных ситуаций.

Метод экспертной оценки, внешняя рецензия, отзыв.

Сроки пробации апрель(1 месяц)

Этапы пробации:

1. Подготовительный. Разработка плана пробации. Знакомство с предметными результатами у учащихся по учебному предмету математика.

2. Практический. Применение разработанного продукта.

3. Аналитический. Оценка деятельности, методического продукта. Создание отчета по результатам практики.

Состав участников. В данном эксперименте участвуют классный руководитель, учителя начальных классов, завуч начальной школы.

База пробации МАОУ «Школа№1» КГО имени Героя Советского Союза Бориса Самуиловича Семёнова класс 2а.

Масштаб пробации. Какое количество уроков, по теме «Нумерация чисел» нами будет разработано и проведено, продолжительность уроков 40 минут, реализация проходила в течении нескольких недель.

Приложение 7

Карта экспертной оценки

Сборников конструктов уроков по математике с использованием проблемного обучения в начальной школе

ФИО эксперта______________________________________________

должность_______________________ Пед. стаж________________

Критерии оценки: 2 – проявляется оптимально 1 – проявляется частично 0 – не проявляется совсем.

Шкала перевода среднего балла: 1,7 - 2 высокий уровень; 1 - 1,6 средний уровень; 0,5 – 0,9 – низкий уровень; 0 – 0,4 недопустимый уровень.

Показатели экспертизы	Оценка эксперта
Актуальность проекта Аргументированность выбранной проблемы Научность Практическая значимость проекта
Оформление проекта Структурированность Систематичность Оформление в соответствии с требованиями
Содержательность проекта Ориентированность проекта на актуальные проблемы возраста детей Направленность на решение проблемы
Удобство в использовании проекта
Общая оценка показателей эксперта
Средняя оценка показателей эксперта

Общий вывод, рекомендации: __________________________

_______________________________________________________________________________________________________________________________________________________________________________________

Подпись эксперта_______________________

Приложение 8

Карта наблюдения за использованием учителем элементов проблемного обучения на уроках математики в начальной школе

1. Пояснительная записка

Цель наблюдения – выявить уровень понимания детьми поставленной учителем проблемной ситуации.

Задачи наблюдения:

• выявить, понимают ли учащиеся созданную проблемную ситуации;

• выяснить, готовы ли учащиеся самостоятельно решить поставленную учителем проблему;

• определить уровень понимания проблемной ситуации и готовности учащихся решить поставленную проблемную ситуацию;

• фиксация результатов в карте наблюдения;

• обработка и анализ зафиксированных результатов.

Объект: обучающиеся начальной школы.

Предмет: понимание созданной проблемной ситуации и способов её решения.

Виды наблюдения:

• по форме организации: структурное наблюдение;

• по степени включенности: включённое наблюдение;

• на основе отношения исследователя к наблюдаемому явлению: открытое наблюдение;

• по месту проведения: естественное наблюдение;

• на основе длительности: кратковременное наблюдение;

• по охвату: выборочное наблюдение;

Сроки и ситуация наблюдения: процедура проводится во время урока 2 раза – в начале исследования и по его завершению.

Теоретическое обоснование:

Процесс использования учителем элементов проблемного обучения на уроках математики в начальной школе. Усвоение учащимися созданной проблемы, её решения, качества понимания новой темы всеми учащимися. В качестве параметра оценивания были выбраны следующие условия применения проблемного обучения на уроке математики в начальной школе.

Со стороны учащихся:

• новая тема (“открытие” новых знаний);

• умение учащихся использовать ранее усвоенные знания и переносить их в новую ситуацию;

• умение определить область “незнания” в новой задаче;

• активная поисковая деятельность.

Условия осуществления наблюдения:

Карта наблюдения заполняется в ходе проведения урока математики, наблюдение осуществляется за деятельностью учащихся (за пониманием ими поставленной проблемной ситуации, также за готовностью решить поставленную проблему).

Условные обозначения или способ фиксации результатов наблюдения:

0 – показатель не проявляется;

1 – показатель проявляется частично;

2 – показатель проявляется в полной мере;

Обработка результатов наблюдения (показатели, как отрабатываются)

Высокий 20-14 баллов (понимание созданной проблемной ситуации, нахождение способов решения поставленной проблемы). Учащиеся в полной меря видят поставленную проблемную ситуацию, самостоятельно без помощи учителя находят решения созданной проблемы.

Средний 13-7 баллов (учащиеся видят созданную проблемную ситуацию, но видят решений поставленной проблемы). Учащиеся видят созданную проблемную ситуацию, но возникают сложности с нахождением способов решения созданной проблемы. Способы решения находятся или с помощью учителя или не находятся совсем.

Низкий 6-0 баллов (полное отсутствие понимания созданной проблемы). Учащиеся не видят созданную проблему, или видят с подсказкой учителя.

Карта наблюдения.

Критерии наблюдения по Бейеру.

Критерии оценивания за использованием учителем технологии проблемного обучения.	ФИО учащихся
1. Определение проблемы. 1.1. Осознают наличие проблемы. 1.2. Осознание ее значения. 1.3. Преобразование проблемы в такой вид, при котором она поддается решению.
2. Выработка возможных вариантов решения проблемы. 2.1. Изучение и классификация теоретических и практических данных. 2.2. Поиск взаимосвязей и построение логических умозаключений. 2.3. Выдвижение гипотез.
3. Проверка гипотезы. 3.1. Сбор данных для анализа. 3.2. Анализ данных, решение проблемы.
4. Выработка заключительного вывода.
5. Практическое применение выводов.