"Декартовая система координат и современность"

31

Міністерство освіти і науки, молоді та спорту України

Управління освіти і науки Донецької облдержадміністрації

Артемівське районне територіальне відділення МАН України

Відділення: математика Секція: математичне моделювання

ДЕКАРТОВА СИСТЕМА КООРДИНАТ І СУЧАНІСТЬ

Роботу виконав:

Добрий Владислав
Сергійович
учень 11 класу
Сіверської
загальноосвітньої
школи
І-ІІІ ступенів №1

Керівник:

Іванова Наталя
Станіславівна,
учитель математики
Сіверської
загальноосвітньої
школи
І-ІІІ ступенів №1
Артемівської районної
ради Донецької області

Сіверськ-2015

Тези до науково-дослідницької роботи з теми

«Декартова система координат і сучасність»

Добрий Владислав Сергійович

Артемівське районне територіальне
математичне відділення МАН

Сіверська загальноосвітня школа

І-ІІІ ступенів №1

учень 11 класу

м. Сіверськ

Керівник

Іванова Наталя Станіславівна,

учитель математики Сіверської
загальноосвітньої школи І-ІІІ
ступенів №1

Мета роботи:

1. розширити сферу знань, де просліджується зв'язок математики та інформатики;

2. Розширити вміння та навики пошуку додаткової інформації, роботи з комп`ютером ;

3. поглибити знання з математики

Об’єкт дослідження: «декартова система координат».

Гіпотеза: людина в своїй діяльності постійно стикається з предметами, які пов’язані з геометричними побудовами

Задачі дослідницької роботи:

1. Закріпити знання отримані в процесі навчання на уроках математики та інформатики.

2. Розширити відомості про історію вивчення систем координат, про побудову різних видів систем координат та використання їх у сучаності

Методи дослідження: аналіз джерел інформації, порівняння, систематизація, узагальнення, моделювання.

Актуальність роботи зумовлена тим, що інтерес до форми якого-небудь предмету може бути продиктований життєвою необхідністю або викликаний красою форми, тому дослідження його важливе не тільки у математичних, а й у життєвих аспектах.

Практичне значення одержаних результатів полягає в тому, що їх можна використати в різних галузях інженерної та проектної діяльності, показати широке використання в сучасному житті.

Наукова новизна роботи полягає в тому, що вона є дослідженням по використанню інформації по роботі в 3D графіці на факультативних заняттях з математики, інформатики та розвитку математичних здібностей нахилів учнів з математики.

Структура роботи

Робота складається із вступу, чотирьох розділів, висновків, списку використаних джерел, додатків. Загальний обсяг роботи 27 сторінок, список використаних джерел включає 9 найменувань.

У вступній частині говориться, що декартова система координат є найбільш вживаною та затребуваною в багатьох сферах та галузях життєдіяльності людини.

Перший розділ присвячений історії розвитку системи координат. Проведено аналіз історичних даних по дослідженню системи координат.

У другому та третьому розділі – узагальнені основні поняття з двовимірного та тривимірного простору. Розглянуто поняття «3D графіка»

Четвертий розділ – систематизовано матеріал щодо побудови графіків на площині та просторі. Виконано практичну роботу по створенню власного макету будівлі у тривимірному просторі, використовуючи комп’ютерні програми Google SketchUp8 .

Завдяки проробленій роботі, я систематизував, вдосконалив, розширив свої знання з даної теми. Значно покращив свої навички та вміння в побудові графіків та переоцінив значущість даної теми в житті людини. Крім того, отримані результати досить цікаві і відкривають широкі перспективи подальшого розвитку роботи і застосування отриманих результатів.

ЗМІСТ

ВСТУП ………………………………………………………………………… 6

Розділ 1 Історія вивчення …………………………………………………….. 8

РОЗДІЛ 2 Загальні поняття………………………………………………… 11

РОЗДІЛ 3 Системи координат……………………………………………… 12

3.1. прямокутна система координат…………………………………… …... 12

3.2. тривимірна система координат……………………………………… … 13

3.3 3D графіка………………………………………………………………… 14

Розділ 4. Побудова графіків ……………………………………………… …. 18

4.1. на площині………………………………………………………………… 18

4.2. в просторі ………………………………………………………………….. 18

4.3 створення проекту у тривимірному просторі…………………………… 19

Висновки ………………………………………………………………………. 21

Список використаних джерел…………………………………………………. 22

Додатки .…………………………………………………………………………. 23

ВСТУП

Координати на площині і в просторі можна вводити нескінченним числом різних способів. Вирішуючи ту або іншу математичну або фізичну задачу методом координат, можна використовувати різні координатні системи, вибираючи ту з них, в якій завдання вирішується простіше або зручніше в даному конкретному випадку. Системи координат в елементарній геометрії — величини, що визначають положення точки на площині і в просторі. За тему для своєї науково-дослідницької роботи я обрав прямокутну та тривимірну систему координат. Ця система є найбільш вживаною та затребуваною в багатьох сферах та галузях життєдіяльності людини. Великої популярності ця система набула через свою простоту, але багатій набір можливого функціоналу. Вона прямо і досить легко узагальнюється для просторів з будь розмірністю, що також сприяє її найширшому застосуванню.

З прямокутною системою координат ми зустрічаємося повсюди. Приходячи до кінотеатру ми бачимо, що кожне місце має свої «координати», тобто номер ряду (вісь ординат) та номер від початку відліку місць (вісь абсцис). Прямокутною системою координат користуються при визначенні географічних координат, нульовий меридіан використовують як вісь ординат, а екватор – як вісь абсцис. Також широкого розповсюдження прямокутна система координат набула в архітектурі, адже архітектори будують схеми будівель за чітким планом, в якому використовують цю систему координат. Прямокутна система координат є невід’ємною частиною в житті економістів, в ній вони будують криві та прямі лінії, що відповідають за попит, пропозицію, ціну, витрати і таке інше, при цьому відслідковують як змінюються якісь складові економіки, як вони взаємодіють.

Тривимірна графіка надійно закріпилася в сучасному житті. Зустрічаємося з нею часто та в багатьох сферах. Не для кого не є новиною фільми з використанням 3D графіки, коли з екранів на нас «дивляться» об’ємні фігури. Без тривимірного моделювання не обходяться комп’ютерні ігри, в яких ми можемо з усіх боків роздивитися будь-яких персонажів, об’єктів і т.д. 3D графіку також використовують деякі інтернет-магазини, щоб покупець зміг повністю оглянути товар. Архітектори також можуть використовувати тривимірну графіку для більш наочного створення моделей конструкцій, будівель і т.і.

Розвиток та вивчення прямокутної системи координат є важливім в сучасному світі швидкого розвитку та динамічних змін, адже з ходом досліджень ми можемо знайти нові шляхи для використання їх в нових галузях, або розвиток в нових аспектах уже в використовуваних галузях.

За метод дослідження даної теми я обрав використання максимальної кількості літератури з складанням основних положень та найголовнішої інформації для систематизації даних саме щодо цієї теми.

Практичне значення одержаних результатів полягає в тому, що їх можна використати в різних галузях інженерної та проектної діяльності, показати широке використання в сучасному житті.

Наукова новизна роботи полягає в тому, що вона є дослідженням по використанню інформації по роботі в 3D графіці на факультативних заняттях з математики, інформатики та розвитку математичних здібностей нахилів учнів з математики.

РОЗДІЛ 1 ІСТОРІЯ ВИВЧЕННЯ

1967 рік – одна з найвизначніших дат в історії математики. Саме в цьому році Рене Декарт (Рис.1) запропонував прямокутну систему координат у своїй праці "Міркування про метод", яку також називають Декартовою системою координат.

Рене Декарт (31 березня 1596 - 11 лютого 1650) — французький філософ, фізик, фізіолог, Рис.1 математик, основоположник аналітичної геометрії. У математиці Декарт запровадив Декартову систему координат, дав поняття змінної величини і функції, ввів багато алгебраїчних позначень. У фізиці він сформулював закон збереження кількості руху, запровадив поняття імпульсу сили. Декарт — автор методу радикального сумніву в філософії, механіцизму у фізиці, передтеча рефлексології.

Наукові досягнення Декарта народилися як « побічний продукт» розроблюваного ним єдиного методу єдиної науки . Декарту належить заслуга створення сучасних систем позначень : він ввів знаки змінних величин ( x , y , z ...), коефіцієнтів ( a , b , c ...), позначення ступенів ( a2 , x-1 ...).

Декарт є одним з авторів теорії рівнянь : їм сформульовано правило знаків для визначення числа позитивних і негативних коренів , поставив питання про межі дійсних коренів і висунув проблему приводимості , тобто представлення цілої раціональної функції з раціональними коефіцієнтами у вигляді твору двох функцій цього роду. Він вказав , що рівняння 3-го ступеня вирішуване в квадратних радикалах ( а також вказав рішення за допомогою циркуля і лінійки , якщо це рівняння приводиться ) .

Рене Декарт є одним з творців аналітичної геометрії (яку він розробляв одночасно з П'єром Ферма) , що дозволяла алгебраїзувати цю науку за допомогою методу координат. Запропонована ним система координат отримала його ім'я.

У роботі « Геометрія» ( 1637р. ) , що відкрила взаємопроникнення алгебри і геометрії , Декарт ввів вперше поняття змінної величини і функції . Мінлива трактується їм двояко: як відрізок змінної довжини і постійного напряму (поточна координата точки , що описує своїм рухом криву ) і як безперервна числова змінна, що пробігає сукупність чисел, що виражають цей відрізок .

В область вивчення геометрії Декарт включив « геометричні » лінії (пізніше названі Лейбніцем алгебраїчними ) - лінії , описувані при русі шарнірними механізмами . Трансцендентні криві (сам Рене Декарт називає їх « механічними » ) він виключив зі своєї геометрії. У зв'язку з дослідженнями лінз в « Геометрії» викладаються способи побудови нормалей і дотичних до плоских кривих .

Його праця «Геометрія» зробила величезний вплив на розвиток математики. У декартовій системі координат отримали реальне тлумачення від'ємні числа. Дійсні числа Декарт фактично трактував як відношення будь-якого відрізка до одиничного (хоча саме формулювання дав пізніше І. Ньютон ) . У листуванні Декарта містяться і інші його відкриття.

Рене Декарт – видатний вчений, ім’я якого навічно залишиться в історії не тільки математики.

Але не лише Декарт вніс свою частку у вивчення прямокутної системи координат. Велику працю над подальшою розробкою цієї системи зробив П'єр Ферма(Рис. 2). Поряд з Декартом, він вважається засновником аналітичної геометрії. У роботі "Вступ до теорії плоских і просторових місць", що стала відомою у 1636, він перший провів класифікацію кривих залежно від порядку їх рівняння, Рис.2 встановив, що рівняння першого порядку визначає пряму, а рівняння другого порядку - конічний перетин. Розвиваючи ці ідеї, Ферма пішов далі Декарта і застосував аналітичну геометрію до простору.

П'єр де Ферма ( 17 серпня 1601 - 12 січня 1665) - французький математик, один з творців аналітичної геометрії, математичного аналізу, теорії ймовірностей та теорії чисел. За професією юрист, з 1631р. - радник парламенту в Тулузі. Блискучий поліглот. Найбільш відомий формулюванням Великої теореми Ферма.

Також над прямокутною системою координат працював Леонард Ейлер (Рис.3) Він першим ввів координатний метод для тривимірного простору.

Леонард Ейлер (15 квітня 1707 - 18 вересня 1783р.) - швейцарський, німецький та російський математик, який зробив значний внесок в розвиток математики, а також механіки, фізики, астрономії та низки прикладних наук.

Рис.3

Ейлер - автор більш ніж 800 робіт за математичного аналізу, диференціальної геометрії, теорії чисел, наближених обчислень, небесній механіці, математичної фізики, оптиці, балістиці, кораблебудування, теорії музики та ін

Майже півжиття провів в Росії, де вніс істотний внесок у становлення російської науки. В 1726р. його було запрошено працювати в Санкт-Петербург, куди переїхав роком пізніше. З 1731р. по 1741р., а також з 1766р. був академіком Петербурзької Академії наук (в 1741 - 1766 роках працював в Берліні, залишаючись одночасно членом Петербурзької Академії почесним). Добре знав російська мова і частину своїх творів (особливо підручники) публікував російською. Деякі з його нащадків до цих пір живуть в Росії.

РОЗДІЛ 2. ЗАГАЛЬНІ ПОНЯТТЯ

Система координат — спосіб задання точок простору за допомогою чисел. Кількість чисел, необхідних для однозначного визначення будь-якої точки простору, визначає його вимірність. Обов'язковим елементом системи координат є початок координат — точка, від якої ведеться відлік відстаней. Іншим обов'язковим елементом є одиниця довжини, яка дозволяє відраховувати відстані. Всі точки одновимірного простору можна задати при обраному початку координат одним числом. Для двовимірного простору необхідні два числа, для тривимірного — три. Ці числа називаються координатами.

Координати на площині і в тривимірному просторі можна задавати нескінченним числом різних способів. Розв'язуючи ту або іншу математичну або фізичну задачу методом координат, можна використовувати різні координатні системи, вибираючи ту з них, в якій завдання розв'язується простіше або зручніше в даному конкретному випадку.

Системи координат в елементарній геометрії — величини, що визначають положення точки на площині і в просторі. На площині положення точки найчастіше визначається відстанями від двох прямих (координатних осей), що перетинаються в одній точці (початку координат) під прямим кутом; одна з координат називається ординатою, а інша — абсцисою. У просторі за системою Декарта положення точки визначається відстанями від трьох площин координат, що перетинаються в одній точці під прямими кутами одна до одної, або сферичними координатами, де початок координат знаходиться в центрі сфери. Стрілки на осях відображають те, що вони простягаються до нескінченості в цьому напрямі.

РОЗДІЛ 3 СИСТЕМИ КООРДИНАТ

3.1 прямокутна система координат

Сучасна Декартова система координат в двох вимірах (також знана під назвою прямокутна система координат) задається двома осями, розташованими під прямим кутом одна до одної. Площину, в якій знаходяться осі, називають іноді xy-площиною. Горизонтальна вісь позначається як x (вісь абсцис), вертикальна як y (вісь ординат). В тривимірному просторі до цих двох додається третя вісь, перпендикулярна xy-площині — вісь z. Всі точки в системі Декартових координат, складають так званий Декартовий простір.

Т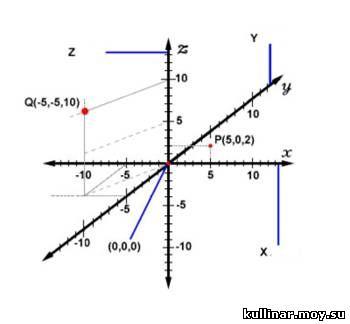очка перетину, де осі зустрічаються, називається початком координат та позначається як O. Відповідно, вісь x може бути позначена як Ox, а вісь y — як Oy. Прямі, проведені паралельно до кожної осі на відстані одиничного відрізку (одиниці виміру довжини) починаючи з початку координат, формують координатну сітку.

Точка в двовимірній системі координат задається двома числами, які визначають відстань від осі Oy (абсциса або х-координата) та від осі Ох (ордината або y-координата) відповідно. Таким чином, координати формують впорядковану пару (кортеж) чисел (x, y). (Рис. 4) Рис.4

Перетин двох осей створює чотири квадранти на координатній площині, які позначаються римськими цифрами I, II, III, та IV. Зазвичай порядок нумерації квадрантів — проти годинникової стрілки, починаючи з правого верхнього (тобто там, де абсциси та ординаті — позитивні числа).

3.2 тривимірна система координат

В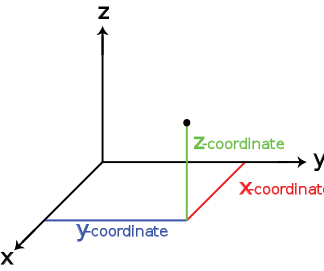 тривимірному просторі до координат x та y додається ще z-координата (відстань точки від ху-площини), та формується впорядкована трійка координат (x, y, z) (Рис.5)

Вибір букв x, y, z походить від загального правила найменування невідомих величин другою половиною латинського алфавіту. Букви першої його половини використовуються для іменування відомих величин. Рис.5

У тривимірній (3d) графіці використовують дві системи координат : правостороння і лівобічна. У обох цих системах Х і Y позитивні, тобто Х дивиться управо Y - вгору. Ви можете запам'ятати позитивний напрям осі Z направляючи палець лівої або правої Вашої руки. Якщо направити великий палець від себе, цей напрям є позитивним по осі Z.

Т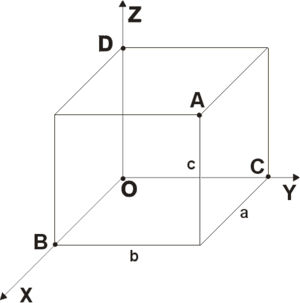ривимірний простір - геометрична модель матеріального світу, в якому ми знаходимося. Це простір називається тривимірним, так воно має три однорідних вимірювання - висоту, ширину і довжину, тобто тривимірний простір описується трьома поодинокими ортогональними векторами. (Рис.6)

Розуміння тривимірного простору людьми, як вважається, розвивається ще в дитинстві, і тісно
Рис.6 пов'язано з координацією рухів людини. Візуальна здатність сприймати навколишній світ органами чуття в трьох вимірах називається глибиною сприйняття.

В аналітичної геометрії кожна точка тривимірного простору описується як набір з трьох величин - координат. Задаються три взаємно перпендикулярних координатних осі, що перетинаються в початку координат. Положення точки задається щодо цих трьох осей завданням впорядкованої трійки чисел. Кожне з цих чисел задає відстань від початку відліку до точки, виміряне уздовж відповідної осі, що дорівнює відстані від точки до площини, утвореної іншими двома осями.

Т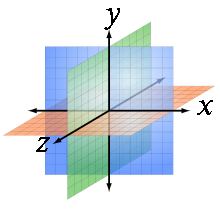ривимірний простір має кілька властивостей, які відрізняють його від просторів іншої розмірності.

Наприклад, це простір найменшою розмірності, в якому можна зав'язати вузол на шматку мотузки. Багато законів фізики, наприклад багато законів зворотних квадратів пов'язані з тим що розмірність нашого просторі три (Рис.7) Рис.7

3.3 3D графіка

Тривимірна графіка — розділ комп'ютерної графіки, сукупність прийомів та інструментів (як програмних, так і апаратних), призначених для зображення об'ємних об'єктів. Найбільше застосовується для створення зображень на площині екрану або аркуша друкованої продукції в архітектурній візуалізації, кінематографі, телебаченні, відеоіграх, друкованій продукції, а також в науці та промисловості (Додаток 1)

Тривимірне зображення на площині відрізняється від двовимірного тим, що включає побудову геометричної проекції тривимірної моделі(сцени) на площину (наприклад, екран комп'ютера) за допомогою спеціалізованих програм. При цьому модель може, як відповідати об'єктам з реального світу (автомобілі, будівлі, ураган, астероїд), так і бути повністю абстрактною (проекція чотиривимірного фрактала).

Для одержання тривимірного зображення на площині потрібні наступні кроки:

Моделювання — створення тривимірної математичної моделі сцени і об'єктів в ній.

Рендеринг (візуалізація) — побудова проекції відповідно до обраної фізичної моделі.

Виведення отриманого зображення на пристрій виведення — дисплей або принтер.

Моделювання

Сцена (віртуальний простір моделювання) включає в себе кілька категорій об'єктів:

• Геометрія (побудована за допомогою різних технік модель, наприклад будівля)

• Матеріали (інформація про візуальні властивості моделі, наприклад колір стін і відбиває / заломлююча здатність вікон)

• Джерела світла (налаштування напрямки, потужності, спектра освітлення)

• Віртуальні камери (вибір точки та кута побудови проекції)

• Сили та дії (налаштування динамічних спотворень об'єктів, застосовується в основному в анімації)

• Додаткові ефекти (об'єкти, що імітують атмосферні явища: світло у тумані, хмари, полум'я і пр.)

Завдання тривимірного моделювання - описати ці об'єкти і розмістити їх у сцені з допомогою геометричних перетворень відповідно до вимог до майбутнього зображення.

Рендеринг — це процес отримання зображення за моделлю з допомогою комп'ютерної програми. Тут модель — це опис тривимірних об'єктів (3D, 3Д) на строго визначеній мові або у вигляді структури даних. Такий опис може містити геометричні дані, положення точки спостерігача, інформацію про освітлення. Зображення — це цифрове растрове зображення. Зазвичай під рендерингом розуміють накладення текстури на готову твердотільну модель (solid-works) у механіці та на каркас (framework) в інженерній графіці.

Візуалізація — один з найбільш важливих розділів в комп'ютерній графіці, і на практиці він найтіснішим чином пов'язаний з іншими. Зазвичай програмні пакети тривимірного моделювання та анімації включають в себе також і функцію рендеринга. Існують окремі програмні продукти, що виконують рендеринг.

Залежно від мети, розрізняють пре-рендерінг, як досить повільний процес візуалізації, що застосовується в основному при створенні відео, і рендеринг в режимі реального часу, застосовуваний у комп'ютерних іграх. Останній часто використовує 3D-прискорювачі.

Тривимірна графіка зазвичай має справу з віртуальним, уявним тривимірним простором, який відображається на плоскій, двомірної поверхні дисплея або аркуша паперу. В наш час відомо кілька способів відображення тривимірної інформації в об'ємному вигляді, хоча більшість з них представляє об'ємні характеристики досить умовно, оскільки працюють з стереообладнанням. З цієї області можна відзначити стереоокуляри, віртуальні шоломи, 3D-дисплеї, здатні демонструвати тривимірне зображення. Декілька виробників продемонстрували готові до серійного виробництва тривимірні дисплеї. Але щоб насолодитися об'ємної картинкою, глядачеві необхідно розташуватися строго по центру. Крок вправо, крок вліво, так само як і необережний поворот голови, карається перетворенням тривимірності в несимпатичне Зазубрене зображення. Вирішення цієї проблеми вже визріло в наукових лабораторіях. Німецький Інститут Фраунгофера демонстрував 3D-дисплей, який за допомогою двох камер відслідковує положення очей глядача і відповідним способом підлаштовує зображення, в цьому році пішов ще далі. Тепер відстежується положення не тільки ока, але і пальця, яким можна «натискати» тривимірні кнопки. А команда дослідників Токійського Університету створили систему що дозволяє відчути зображення. Випромінювач фокусується на точці де знаходиться палець людини і залежно від його положення змінює силу акустичного тиску. Таким чином, стає можливим не тільки бачити об'ємну картинку, але й взаємодіяти із зображеними на ній предметами.

Однак і 3D-дисплеї, як і раніше не дозволяють створювати повноцінної фізичної, відчутної копії математичної моделі, створюваної методами тривимірної графіки.

РОЗДІЛ 4. ПОБУДОВА ГРАФІКІВ

4.1 на площині

Для побудови точок на площині використовують 2 координати: Х та У. Точку задають у вигляді: А (х; у), де А – назва точки, а х і у – координати.
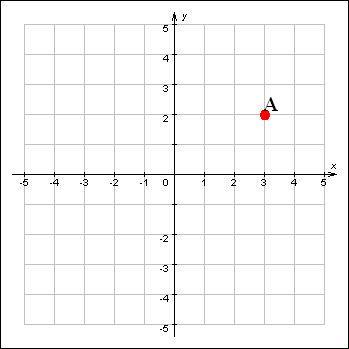
Для прикладу задамо точку А, з координатами 3 по вісі ОХ, та 2 по вісі ОУ, тобто: А(3;2) (Додаток 2 – рис.1). На плоскій системі координат можна вибудовувати різні плоскі геометричні фігури за вершинами: трикутники, квадрати, прямокутники і т.д. і т.і.

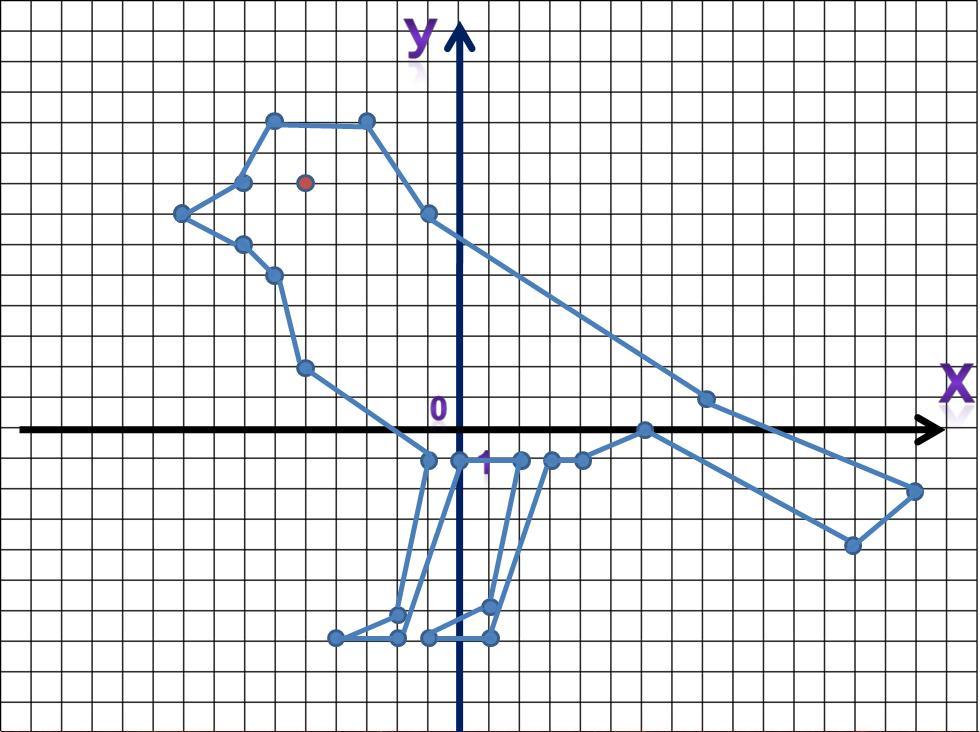
При грамотному задані точок, та правильному послідовному їх з’єднанні можна навіть отримати цікаві зображення. Наприклад, якщо вибудувати точки A(-9;7), B(-7;8), C(-6;10), D(-3;10), E(-1;7), K(8;1), R(15;-2), T(13;-4), Y(6;0), U(4;-1), I(3;-1), O(1;-7), P(-1;-7), S(1;-6), F(2;-1), G(0;-1), H(-2;-7), J(-4;-7), L(-2;-6), Z(-1;-1), X(-5;2), V(-6;5), N(-7;6), M(-9;7) та послідовно їх з’єднати, виділивши окрему точку Q(-5;8), отримується приблизно така картина в системі координат (Додаток 2 – рис.2).

Це звичайно прості та навіть дитячі вправи, але вони допомагають новачкам в цій справі «набити» руку в побудові точок. Тому розглянемо ще один приклад. Вибудуємо точки (9;4), (9;5), (8;9), (8;11), (9;12), (9;14), (8;15),(7;15), (5;13), (5;12), (4;11), (2;10), (4;9), (5;9), (5;7), (4;7), (4;5), (5;6), (5;3), (4;3), (4;1), (3;1), (3;0), (5;0), (5;2), (7;2), (7;1), (9;1), (9;0), (10;0), (10;2),(8;2),(9;3), (9;4), (11;4), (11;9), з’єднаємо їх послідовно, та окремо побудуємо точку (5; 11), отримуємо наступне(Додаток 2- рис. 3).

4.2 в просторі

Для побудови певних точок в просторі двох координат буде недостатньо, тому вводиться третя координата z. При побудові точки в просторі, запис має вигляд A(x; y; z), де А – назва точки, x, y, z – координати точки. Схему побудови точки показано на рисунку (Додаток 2 – рис.4).

Побудова точок та фігур в просторі є більше робото ємкісною, нуж на площині. Але при вмілому задані точок на виході отримуємо повноцінний об’єкт, який можна покрутити, повернути та розглянути з усіх боків (якщо це створено за допомогою комп’ютерних технологій).

Адже саме завдяки тривимірній графіці ми маємо змогу спостерігати, наприклад, персонажів відеогри з усіх його боків. Завдяки тривимірній графіці ми можемо відтворити, наприклад, ландшафт певної території, з усіма нерівностями, вгинами, впадинами і т.д., а при переведенні даних в комп’ютерну модель, можемо навіть роздивитися її з усіх сторін.

Завдяки побудові в третьому вимірі, ми маємо змогу навіть на площині зобразити об’ємні фігури, такі як куб, піраміда, циліндр, призма і т.д. і т.п.

4.3. Створення проектів у тривимірному просторі

Багато хто думає, що комп'ютерна графіка - це в першу чергу ігри з віртуальною реальністю і рекламні ролики, а "потрібність" і "корисність" як того, так і іншого очевидна далеко не всім. Між тим, комп'ютерна графіка - це наука. Хто не згоден з цим, погодиться хоча б, що це інструмент. Сам по собі інструмент не може бути ні добре, ні погано, ні шкідливий, ні корисний, ні навіть даремний. Все залежить від конкретних програм.

В даний час під комп'ютерною графікою розуміють автоматизацію процесів підготовки, перетворення, зберігання і відтворення графічної інформації за допомогою комп'ютера. Під графічною інформацією розуміються моделі об'єктів і їх зображення. Інтерактивна комп'ютерна графіка - це так само використання комп'ютерів для підготовки і відтворення зображень, але при цьому користувач має можливість оперативно вносити зміни в зображення безпосередньо в прецесійного відтворення, тобто передбачається можливість роботи з графікою в режимі діалогу в реальному масштабі часу. Інтерактивна графіка являє собою важливий розділ комп'ютерної графіки, коли користувач має можливість динамічно керувати вмістом зображення, його формою, розміром і кольором на поверхні дисплея за допомогою інтерактивних пристроїв управління.

Я вирішив власноруч спробувати створити макет будівлі у тривимірному просторі, використовуючи комп’ютерні програми Google SketchUp8 (Додаток 3). Програма Google SketchUp8 - програма для розробки тривимірних моделей будинків, гаражів, терас, прибудов, дерев'яних проектів і навіть космічних кораблів. Вона проста у використанні, завдяки їй, можна створювати і модифікувати тривимірні моделі будинків, об'єктів та інших архітектурних споруд.

Редактор створений з розрахунком на непрофесіоналів і дозволяє створювати макети з використанням звичних інструментів - «лінійка», «олівець», «транспортир», «гумка» в трьох площинах. Однак, незважаючи на простоту Google SketchUp надає користувачам такі корисні функції, як:

• можливість задавати точні розміри в міліметрах;

• використання шарів;

• можливість завантажувати готові 3D моделі

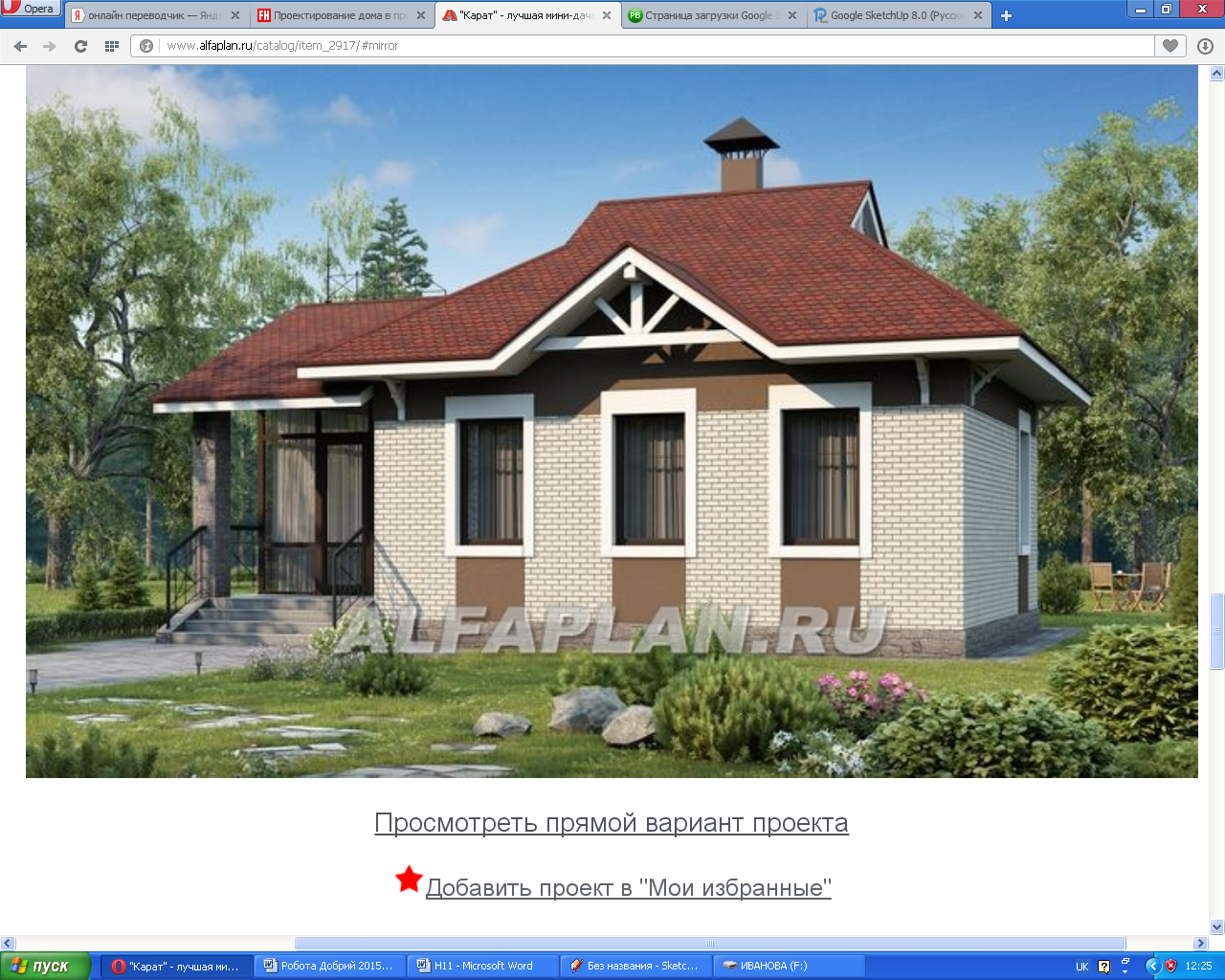
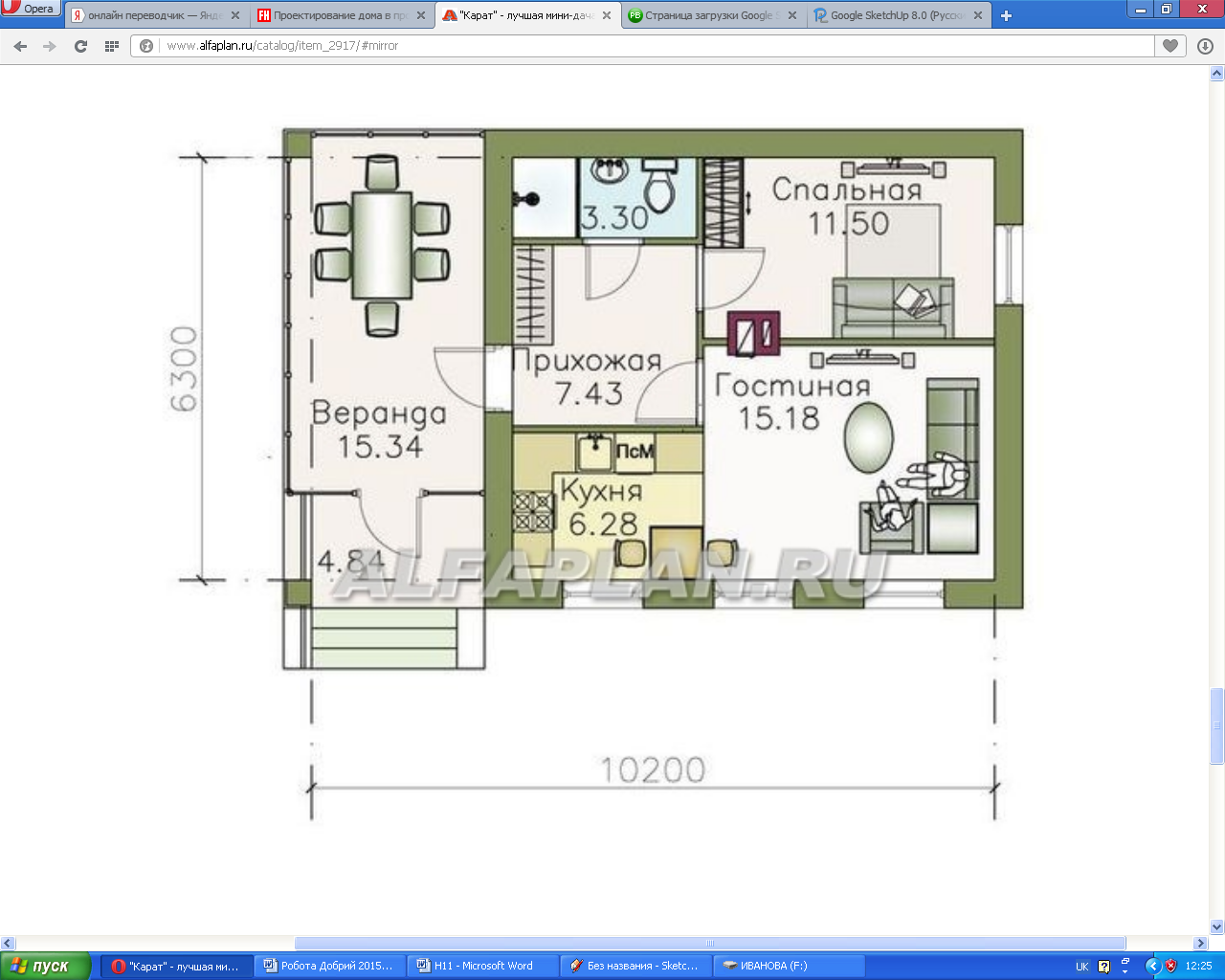
Проект будинку можна створювати різного ступеня деталізації (Додаток 4).
Опрацювавши матеріал з математичної точки зору та поспілкувавшись з вчителем інформатики, я дійшов висновку, що можна змоделювати будинок моєї мрії, тим самим поглибивши знання в комп’ютерній графіці.

ВИСНОВКИ

Завдяки проробленій роботі, я систематизував, вдосконалив, розширив свої знання з даної теми. Значно покращив свої навички та вміння в побудові графіків та переоцінив значущість даної теми в житті людини.

Дана робота містить інформацію, яка була б цікавою для учнів загальноосвітніх шкіл, для слухачів факультативних курсів, так як показує зв'язок між шкільним курсом математики та сучасними інформаційними технологіями.

Історії вивчення математики на уроках відводиться незначна роль, тому інформація, яка містить в роботі є пізнавальною та розширює кругозір учнів.

Працюючи над роботою я розширив свої вміння працювати з довідковою літературою, знаходити інформацію в мережі інтернет, робити висновки.

Я виявив, що мені цікаво працювати з комп'ютерною графікою. Створювати нові проекти, редагувати вже створені з урахуванням нових технологій і можливостей. 

Знання, які здобув в процесі роботи над проблемою, зможу використати під час навчання у вищому навчальному закладі, в який думаю вступити в 2015 році.

Під час виконання науково-дослідницької роботи спробував побудувати в тривимірному просторі деякі макети власноруч, упевнився в практичній значимості математики, адже засобами моделювання можна розробити дизайн будинку, приміщення та зробити певні обчислення , тим самим, вибрати найекономніший варіант.

Крім того, отримані результати досить цікаві і відкривають широкі перспективи подальшого розвитку роботи.

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

1. Самин Д. К. 100 великих ученых. - М.: Вече, 2000

2. Корн Г., Корн Т. Справочник по математике. — М.: Наука, 1974. — 832 с.(С. 519) (рос.)

3. Дж. Лі, Б. Уер. Тривимірна графіка та анімація. — 2-е вид. — М.: Вільямс, 2002. —640 с.

4. Кантор Г. Труды по теории множеств. — Москва: Наука, 1985..

5. 5. Гельфанд И. М., Глаголева Е. Г., Кириллов А. А. Метод координат. Издание пятое, стереотипное. Серия: Библиотечка физико-математической школы. Математика. Выпуск 1. М.: Наука, 1973.

6. www.informic.narod.ru 

7 . www.infoschool.narod.ru 

8. www.klyaksa.ru 
9. www.problems.ru 

Додаток 1

Додаток 2

Рис.1 Рис.2

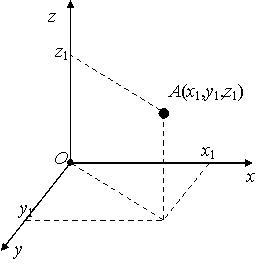
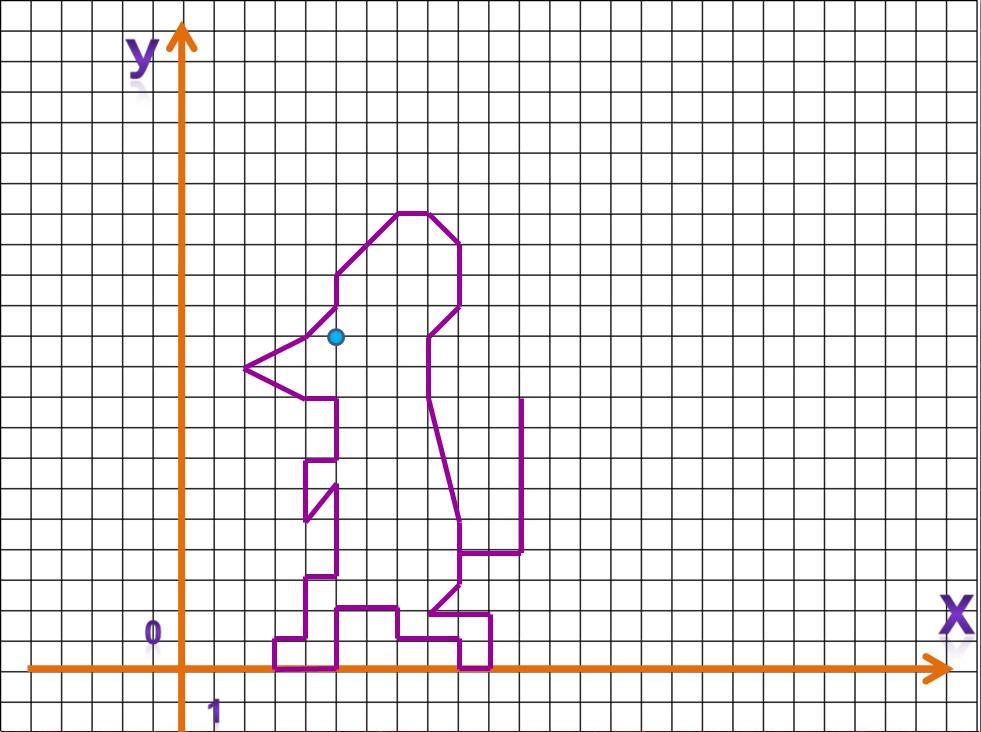
Рис.3 Рис.4

Додаток 3

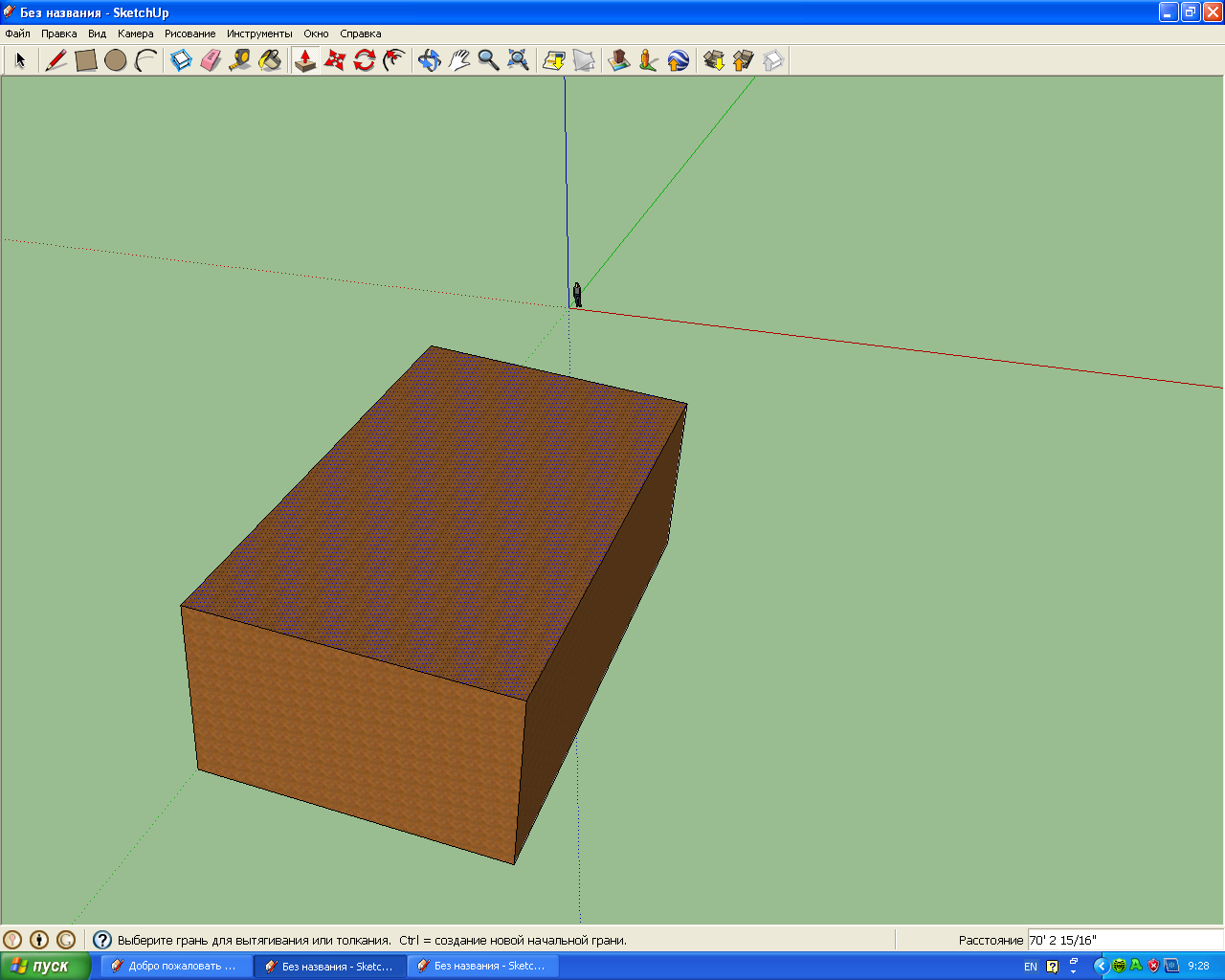
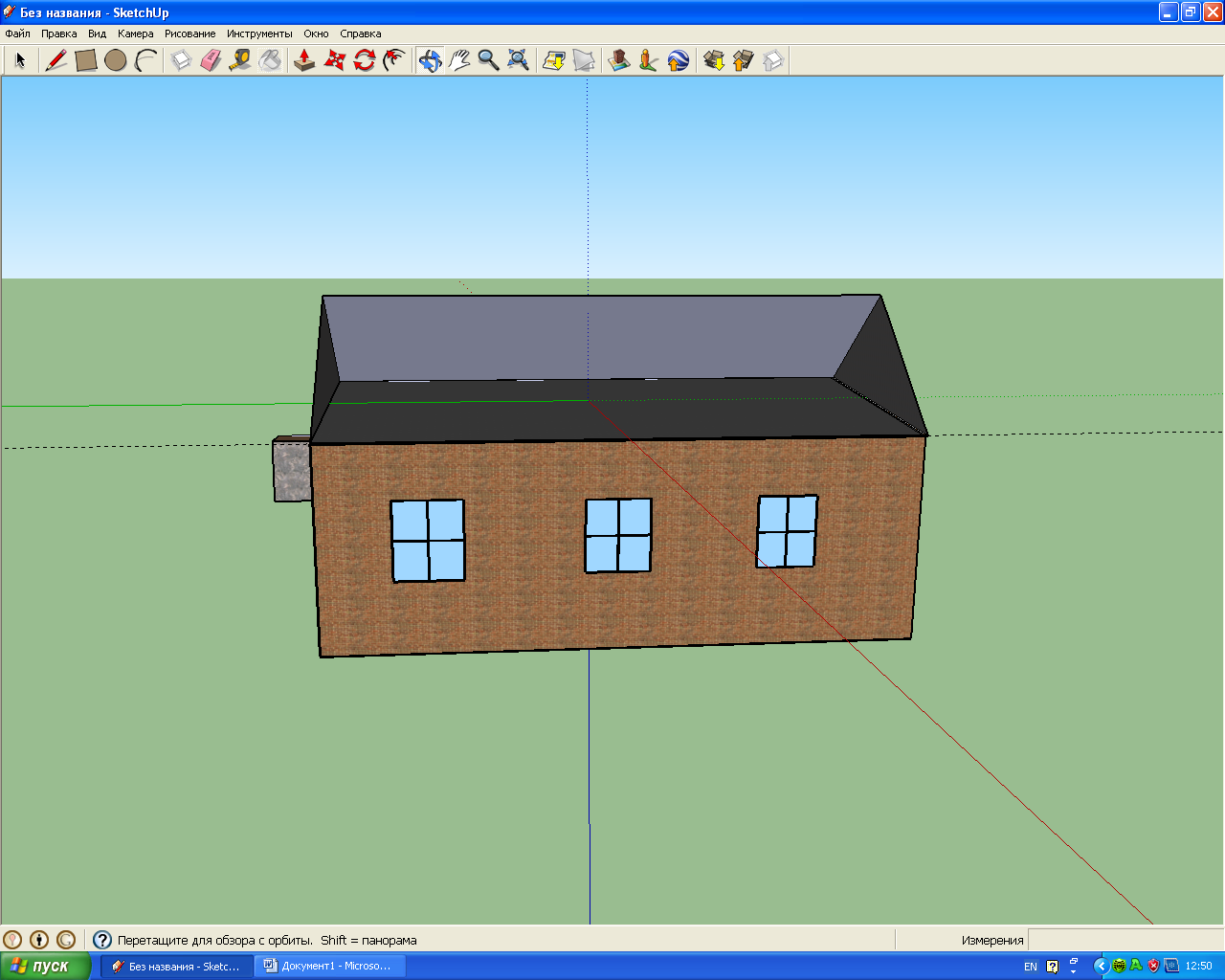
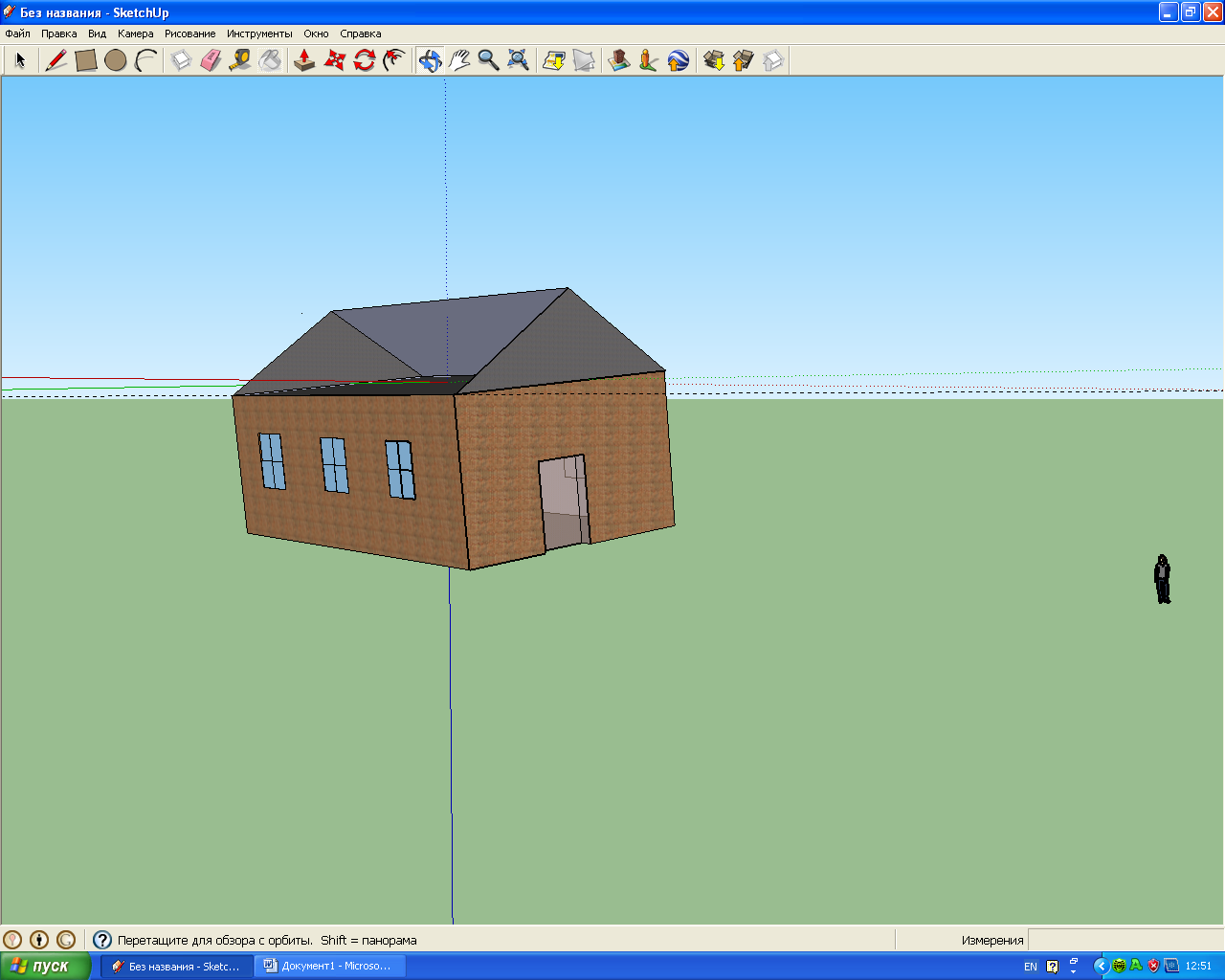
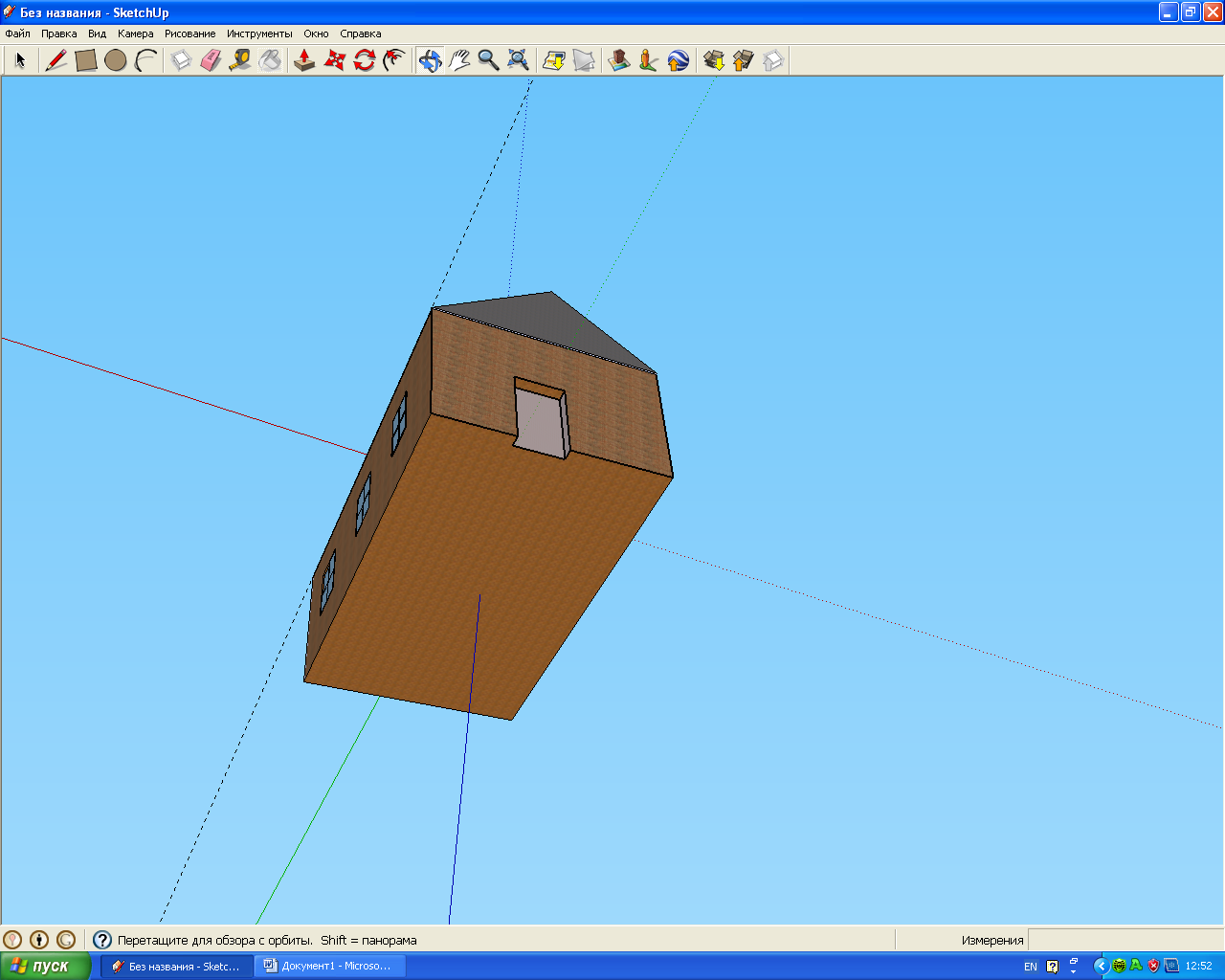
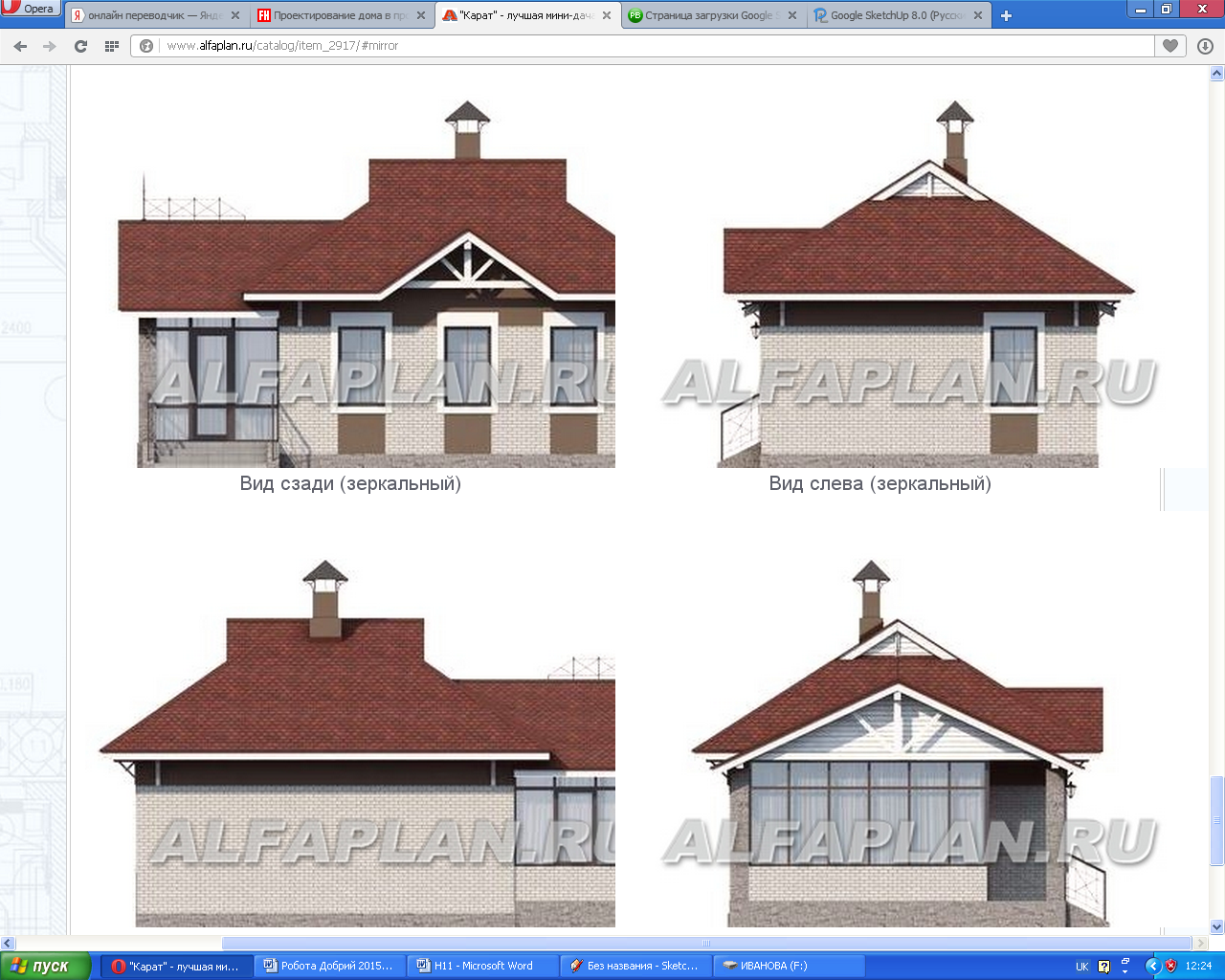Додаток 4

ВІДГУК

на дослідницьку роботу учня 11 класу

Сіверської загальноосвітньої школи І-ІІІ ступенів №1

Доброго Владислава Сергійовича

«Декартова система і сучасність»

Серед численних інтересів учня 11 класу, Доброго Владислава, пріоритетною сферою є математика. Його дослідницька робота - результат захоплення геометричними перетвореннями.

Мета роботи – розширити сферу знань, де просліджується зв'язок математики та інформатики, розширити вміння та навики пошуку додаткової інформації, роботи з комп`ютером. Матеріал роботи викладено аргументовано, послідовно і логічно, оформлено згідно вимог. Під час виконання роботи учень проявила самостійність, достатню грамотність, відповідальність та готовність до наукової діяльності. Добрий Владислав спирається на доступну базу джерел, володіє добрими знаннями в галузі досліджуваного матеріалу.

Ілюстративний матеріал, дібраний учнем та використаний у роботі, для підтвердження своєї гіпотези, є доречним, науково вірогідним, вагомим. Важливим у роботі є створення власних макетів та використання їх в повсякденному житті. В цілому дослідження концептуальне, його продумана структура дає змогу висвітлити обрану тему глибино.

Учень довів, що інтерес до декартової системи координат обумовлений застосуванням його в комп’ютерній графіці, яка допомагає штучно створювати природні явища та лінії. Тому дослідження Доброго В. досить самостійні.

Керівник районного методичного

об’єднання вчителів математичного циклу О.С.Федоренко