Задания типа В5, про лабиринт
Подготовила: Калаева Татьяна Олеговна учитель МБОУ СОШ №16 г. Владимира
Владимир, 2014
Содержание
| Введение | 3 |
| Глава 1. Пространство элементарных событий | 4 |
| 1.1 Случайные события | 5 |
| 1.2 Формула классической вероятности | 6 |
| 1.3 Несовместные события. Формула сложения вероятностей | 6 |
| 1.4 Совместные события. Формула сложения вероятностей | 6 |
| 1.5 Независимые событий. Формула умножения вероятностей | 7 |
| 1.6 Контрольные вопросы | 7 |
| Глава 2. Задания В6, про лабиринт | 8 |
| 2.1 Разбор задания на примере | 8 |
| 2.2 Задачи для самостоятельного решения | 9 |
| 2.3 Ответы на задачи для самостоятельного решения | 12 |
| Список использованной литературы | 13 |
Введение
До возникновения теории вероятностей объектом исследования науки были явления или опыты, в которых условия практически однозначно определяют исход. Классическим примером является механика. Пусть, например, на материальную точку действует сила тяжести. Если в некоторый момент задать положение и скорость материальной точки, то ее дальнейшее движение определяется однозначно. Однако, если эту механическую модель применить к реальным физическим телам, например рассматривать движение пули, то однозначная траектория уже не будет определяться. Начальная скорость заранее точно не известна; при различных выстрелах она может принимать различные значения. Таким образом, неопределенность здесь вносится случайностью начальной скорости.
Неоднозначность исхода при сохранении основных условий опыта сохраняется для широкого круга явлений. При подбрасывании монеты мы не можем предсказать исход: выпадет монета верх гербом или нет. Результаты нескольких измерений, полученных одним и тем же прибором в одинаковых условиях, различны. Влияние очень большого числа разнообразных причин, каждая из которых в отдельности не может повлиять на результат опыта, приводит к тому, что результат опыта не определяется заранее однозначно: говорят, что результат такого опыта случаен.
Примеры случайных явлений можно указать во многих областях науки и техники (например, в физике, биологии, демографии, в массовом производстве и т.д.).
Индивидуальные результаты опытов, подбрасываний монеты, измерений, ведут себя очень «неправильно». Однако при наблюдении результатов большой последовательности опытов обнаруживаются интересные закономерности. Если обозначить NГ число выпадений герба при N подбрасывании монеты, то оказывается, что частота NГ/N с ростом N становится близкой к 1/2. Это явление имеет общий характер.
Изучением случайных явлений занимается теория вероятностей. Каждому событию приписывается особая числовая мера объективной возможности его появления – вероятность.
Пространство элементарных событий
Чтобы избежать неясностей при описании случайных явлений, результатов опытов или наблюдений, мы введем ряд точных понятий. Назовем произвольное множество Ω пространством элементарных событий. Элементы ω этого множества Ω будем называть элементарными событиями. Эти понятия являются первоначальными. В реальном опыте элементарным событиям соответствуют взаимоисключающие исходы. Ввиду большого разнообразия случайных явлений нельзя дать более конкретно определение множества элементарных событий. Для описания каждой реальной задачи множество Ω выбирается наиболее подходящим образом. Рассмотрим примеры.
Подбрасывание монеты один раз
Возможными исходами в этом опыте будут: выпадение герба, выпадение решки. Кроме того, монета возможно встанет на ребро, укатиться куда-нибудь и т. д. При математическом описании этого опыта естественно отвлечься от ряда несуществующих исходов и ограничиться только двумя: выпадение герба (ωГ), выпадение решки (ωР). Таким образом, при описании этого опыта мы полагаем
Ω={ωГ, ωР}.
Подбрасывание игральной кости один раз
В этом опыте естественно выбрать Ω={ω1, ω2, ω3, ω4, ω5, ω6}, где ωk обозначен исход опыта, заключающийся в выпадении k очков. Имеем шесть исключающих друг друга исходов.
Одна монета подброшена n раз
Каждому исходу опыта естественно поставить в соответствие последовательность длины n по следующему правилу: если при k-ом подбрасывании монеты выпал герб, то на k-ом месте последовательности пишем Г, а при выпадении решки – Р. Так последовательность ГГГ…ГГ обозначает исход опыта, заключающийся в том, что каждый раз выпал герб. Элементарное событие
соответствуют исходу, в котором монета сначала подряд m падала гербом вверх, а оставшиеся n – m раз – решкой вверх. Таким образом, множество Ω состоит из всевозможных последовательностей длины n вида: РГРРГ…РГР. При небольших значениях n все элементарные события нетрудно выписать. Например, при n=3
Ω={ГГГ, ГГР, ГРГ, ГРР, РГГ, РГР, РРГ, РРР}.
Нетрудно проверить, что число элементарных событий при любом n равно 
. Действительно, все цепочки длины n можно разбить на две группы цепочек вида
{Г…} , {РР…}.
Случайные события
Случайными событиями или просто событиями будем называть подмножество A множества Ω.
Случайные события обычно обозначаются большими латинскими буквами A, B, C, D и т.д.
Суммой двух событий A и B назовем событие A+B, состоящее из всех элементарных, принадлежащих, по крайней мере, одному из событий A или B. Можно сказать, что в реальном опыте событие, соответствующее A+B, состоит в том, что произошло A или B.
Произведением АВ называется событие, состоящее из элементарных событий, принадлежащих и А и В. Событие АВ происходит тогда и только тогда, когда происходит и А и В. (на рисунке показано синим цветом).
Формула классической вероятности
Вероятностью Р события А называют отношение числа m исходов, благоприятных этому событию, к общему числу n исходов 
. Сумма всех элементарных событий случайного эксперимента равна 1.
Несовместные события. Формула сложения вероятностей
События называют несовместными, если они не могут происходить одновременно в одном и том же испытании.
Например, выигрыш, проигрыш и ничейный исход одного игрока в одной партии в шахматы – три несовместных события.
Теорема. Вероятность суммы двух несовместных событий А и В (появления хотя бы одного события) равна сумме вероятностей этих событий:
Р(А+В)=Р(А)+Р(В).
Теорема обобщается на любое число попарно несовместных событий.
Совместные события. Формула сложения вероятностей
Рассмотрим формулу для вероятности суммы двух событий в общем случае (не обязательно несовместных).
События называются совместными, если они могут происходить одновременно. Например, при бросании двух монет выпадение решки на одной не исключает выпадение решки на другой монете.
Вероятность суммы двух совместных событий A и В (появления хотя бы одного события) равна сумме их вероятностей без вероятности их совместного появления, то есть
Р(А+В) = Р(А) + Р(В) – Р(АВ).
Независимые события. Формула умножения вероятностей
Два случайных события называются независимыми, если наступление одного из них не изменяет вероятность наступления другого. В противном случае события называют зависимыми.
Теорема. Вероятность произведения (совместного появления) двух независимых событий равна произведению вероятностей этих событий:
Р(АВ) = Р(А) · Р(В).
Теорема обобщается на любое число попарно независимых событий.
Контрольные вопросы
Симметричную монету подбрасывают один раз. Будем обозначать выпадение орла ωО, а выпадение решки ωР. Выпишите все элементарные события этого опыта.
Симметричную монету подбрасывают два раза. Будем обозначать выпадение орла ωО, а выпадение решки ωР. Выпишите все элементарные события этого опыта.
Сколько элементарных событий при трех подбрасываниях симметричной монеты?
Игральную кость подбрасывают один раз. Сколько элементарных событий в этом эксперименте.
Учитель нарисовал на доске квадрат ABCD и предлагает учащемуся выбрать две вершины. Сколько элементарных событий в этом опыте?
Игральный кубик бросают дважды. Сколько элементарных исходов опыта благоприятствуют событию «А – сумма очков равна 10»?
Найти вероятность выпадение орла при подбрасывании симметричной монеты.
Найти вероятность выпадение четного числа при подбрасывании игральной кости.
Монету подбрасывают два раза. Найти вероятность выпадения орла в обоих случаях.
Задача B5, про лабиринт
Рассмотрим задачу. На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может, поэтому на каждом разветвлении паук выбирает один из путей, по которому ещё не полз. Считая, что выбор дальнейшего пути чисто случайный, определите, с какой вероятностью паук придёт к выходу D.
Решение: На каждой из четырех отмеченных развилок паук с вероятностью 0,5 может выбрать или путь, ведущий к выходу D, или другой путь. Это независимые события, вероятность их произведения (паук дойдет до выхода D) равна произведению вероятностей этих событий. Поэтому вероятность прийти к выходу D равна (0,5)4 = 0,0625.
Ответ: 0,0625.
Задачи для самостоятельного решения1
№ 322923. На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может. На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук придёт к выходу D.
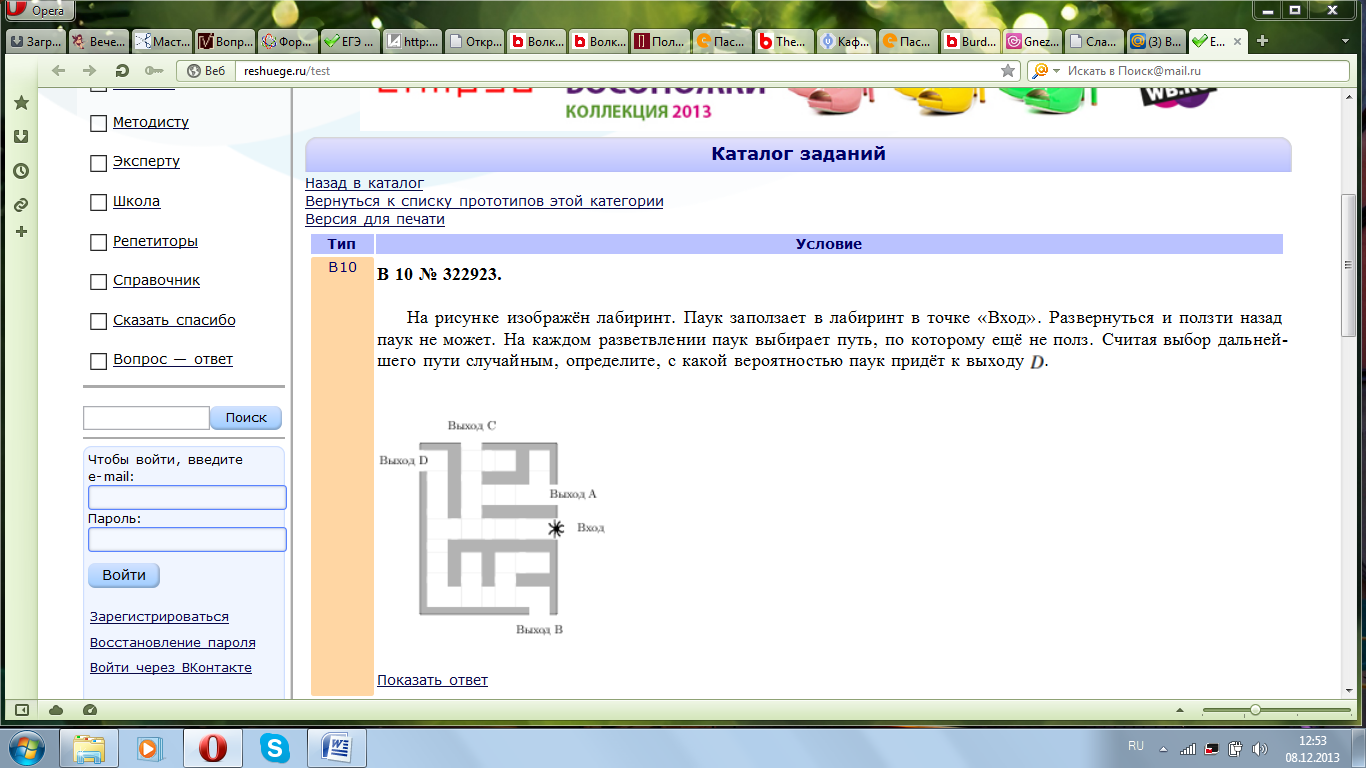
№ 322925. На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может. На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук придёт к выходу D.
№ 322927. На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может. На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук придёт к выходу A.
№ 322929. На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может. На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук придёт к выходу A.
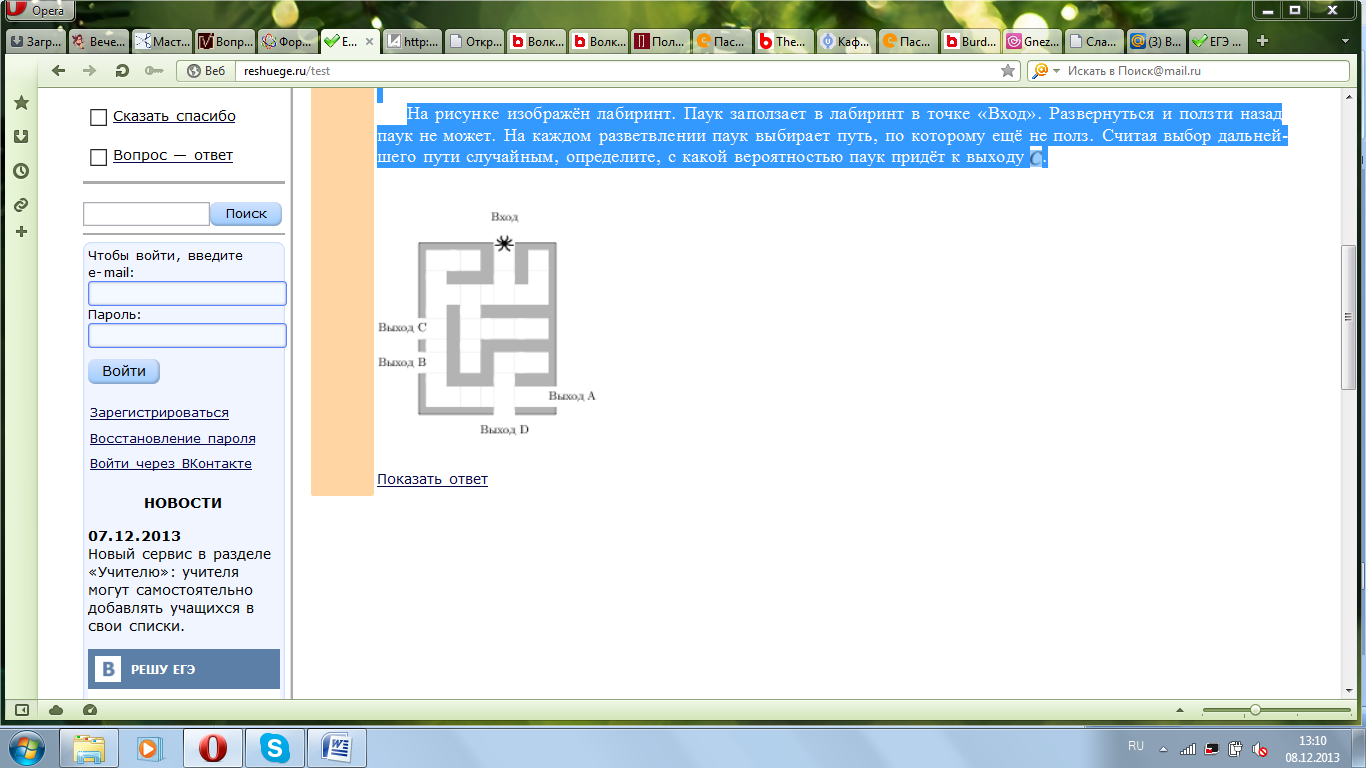
№ 322931. На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может. На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук придёт к выходу D.
№ 322933. На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может. На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук придёт к выходу A.
№ 322935. На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может. На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук придёт к выходу C.
№ 322937. На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может. На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук придёт к выходу A.
№ 322939. На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может. На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук придёт к выходу A.
№ 322941. На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может. На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук придёт к выходу A.
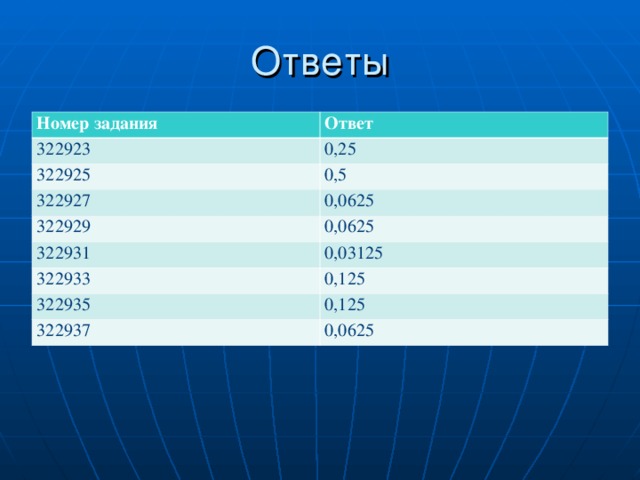
Ответы к заданиям для самостоятельного решения
| Номер задания | Ответ |
| 322923 | 0,25 |
| 322925 | 0,5 |
| 322927 | 0,0625 |
| 322929 | 0,0625 |
| 322931 | 0,03125 |
| 322933 | 0,125 |
| 322935 | 0,125 |
| 322937 | 0,0625 |
| 322939 | 0,5 |
| 322941 | 0,25 |
Список использованной литературы
Курс теории вероятностей. В.П. Чистяков. М: «Наука», 1978, 224стр.
Интернет-ресурс: Решу ЕГЭ. Образовательный портал для подготовки к экзаменам // http://reshuege.ru
Корянов А.Г., Надежкина Н.В. Задания В10. Элементы теории вероятностей // http://alexlarin.net
