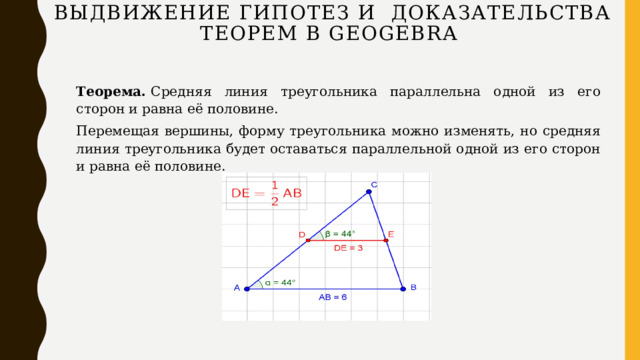
С помощью интерактивной геометрической среды GeoGebra можно не только визуализировать процесс обучения геометрии, делать его более наглядным и интересным, но и доказывать теоремы и решать задачи, выдвигать гипотезы, подтверждать или опровергать их, проводить компьютерные эксперименты и т.п.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Возможности системы Geogebra для проверки гипотез и доказательства теорем
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Возможности системы Geogebra для проверки гипотез и доказательства теорем»
Полезное для учителя
Распродажа видеоуроков!
1690 руб.
2820 руб.
1900 руб.
3170 руб.
1060 руб.
1760 руб.
1720 руб.
2860 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства