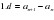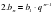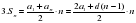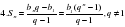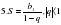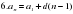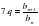| Вводная часть |
| Организационный момент. Стратегия «Мозговой штурм» (Актуализация знаний и умений) 1) Повторить определения прогрессий. 2) Работа с формулами. Восприятие речи на слух. Учитель проговаривает название формулы один раз, а учащиеся пишут номер формулы СЛАЙД Формулы. 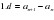
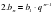
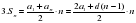
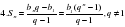
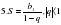
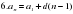
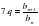
СЛАЙД Листочки с каждого ряда собирает дежурный помощник. Выполняем проверку по коду. Получили 7-значное число 5834291. Это КОД ОТВЕТА. Проверка домашнего задания. Сообщаются краткие исторические сведения, приготовленные учащимися. СЛАЙД 5 СЛАЙД 6,7 СЛАЙД 8 СЛАЙД 9
| Психологический насторй учащихся на дальнейшую деятельность. Эпиграф урока. Закончился XX век. Куда стремится человек? Изучены космос и море, Строенье звёзд и вся Земля. Но математиков зовёт Известный лозунг: “Прогрессио – движение вперёд”.
Каждый ученик может ответить на вопросы и заработать себе баллы:
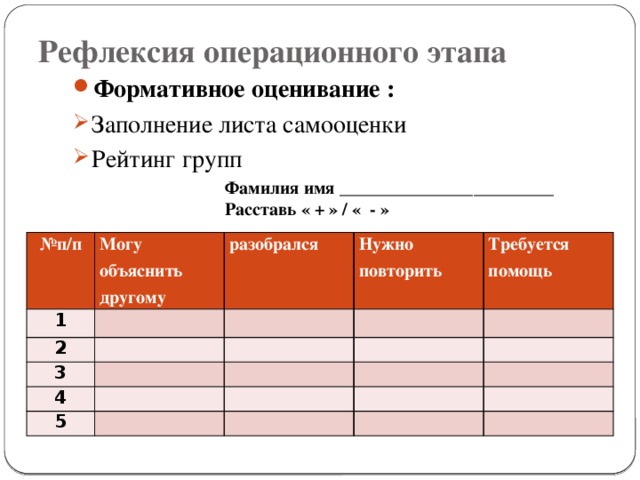
Стратегия « Две звезды и одно пожелание»
Группа1: Последовательности (сообщение) Фундаментальную роль числа в природе определил еще Пифагор своим утверждением "Все есть число". Поэтому математика являлась одной из основ религии последователей Пифагора (пифагорейского союза). Пифагорейцы считали, что бог Дионис положил число в основу мировой организации, в основу порядка; оно отражало единство мира, его начало, а мир представлял собой множество, состоящее из противоположностей. То, что приводит противоположности к единству, и есть гармония. Гармония является божественной и заключается в числовых соотношениях. Слово «прогрессия» латинского происхождения (progressio), буквально означает «движение вперед» ( как и слово «прогресс») и встречается впервые у римского автора Боэция (V-VI вв.). Прогрессии известны издавна, а потому нельзя сказать, кто их открыл. Ведь и натуральный ряд – это арифметическая прогрессия. Во время раскопок в Египте был найден папирус, который датируется 2000 г. до н.э., но и его было переписано из другого, еще более раннего, отнесенного к ІІІ тысячелетию до н.э. Ученые расшифровали текст папируса, содержание некоторых задач дает возможность отнести их к задачам на прогрессии. Группа 2: В вавилонских текстах рассказывается о том, что увеличение освещенной части лунного диска на протяжении первых пяти дней происходит по закону геометрической прогрессии со знаменателем 2, а в следующие десять дней – по закону арифметической прогрессии с разностью 16. Задачи на прогрессии встречаются в одной из древнейших памяток права – «Русской правде», составленной при Киевском князе Ярославе Мудром (ХІ ст.). В этом документе есть статья, посвященная вычислению приплода от 22 овец за 12 лет при условии, что каждая овца ежегодно приносит одну овцу и два барана. Так же содержатся сведения о приплоде от пчел за определенный промежуток времени, о количестве зерна, собранного на определенном участкае земли и др. Эти задачи не имели хозяйственного значения, а были результатом развития интереса к математике и математическому содержанию данных задач.
О том, как давно была известная геометрическая прогрессия, свидетельствует и легенда об истории изобретения шахмат. Изобретатель шахмат, ученый Сета, попросил в награду у индийского царя Сирама за свое изобретение столько пшеничных зерен, сколько их получится, если на первую клеточку шахматной доски положить одно зерно, на вторую – два, на третью- четыре, т.е. чтобы число зерен все время удваивалось. Рассказывают, что индийский царь Сирам рассмеялся, услышав, какую награду попросил у него изобретатель шахмат. Сколько зёрен должен был получить изобретатель шахмат? (Учащиеся должны подсчитать дома) S64 = 264 – 1 = 18 446 744 073 709 551 615.
18 квинтильонов 446 квадрильонов 744 триллиона 73 миллиарда (биллиона) 709миллионов 551 тысяча 615.
Современники сказали бы так: S64 = 1, 84• 1019 – стандартный вид данного числа. Группа 3: Если бы царю удалось засеять пшеницей площадь всей поверхности Земли, считая и моря , и океаны, и пустыни, и Арктику с Антарктикой, то получить удовлетворительный урожай, то за пять лет он смог бы рассчитаться с просителем. Такое количество зерен пшеницы можно собрать лишь с площади в 2000 раз большей поверхности Земли. Это превосходит количество пшеницы, собранной человечеством до нашего времени. Чтобы разместить это зерно в амбаре, то его размеры будут: высота 4 м, ширина 10м, длина будет 30 000 000км- вдвое больше, чем расстояние от Земли до Солнца |
|
| карточки | Группа 1: Больной принимает лекарство по следующей схеме: в первый день он принимает 5 капель, а в каждый следующий день — на 5 капель больше, чем в предыдущий. Приняв 40 капель, он 3 дня пьет по 40 капель лекарства, а потом ежедневно уменьшает прием на 5 капель, доведя его до 5 капель. Сколько пузырьков лекарства нужно купить больному, если в каждом содержится 20 мл лекарства (что составляет 250 капель)? Группа 2: Улитка ползет по дереву. За первую минуту она проползла 30 см, а за каждую следующую минуту — на 5 см больше, чем за предыдущую. За какое время достигнет улитка вершины дерева длиной 5,25 м, если считать, что движение начато от его основания? Группа 3: Альпинисты в первый день восхождения поднялись на высоту 1400 м, а затем каждый следующий день они проходи ли на 100 м меньше, чем в предыдущий. За сколько дней они покорили высоту в 5000 м?
Группа 4: За изготовление и установку самого нижнего железобетонного кольца колодца заплатили 26 условных единиц (у. в.). а за каждое следующее кольцо платили на 2 у. е. меньше, чем за предыдущее. Кроме того, по окончании работы было уплачено ещё 40 у. е.. Средняя стоимость изготовления и установки кольца оказалась равной 22 и 4/9 у. е.. Сколько колец было установлено? Группа 5: В соревновании по стрельбе за каждый промах в серии из 25 выстрелов стрелок получал штрафные очки: за первый промах — одно штрафное очко, за каждый последующий — на 0,5 очка больше, чем за предыдущий. Сколько раз попал в цель стрелок, получивший 7 штрафных очков?
Самооценка. Фамилия имя ________________________ Расставь « + » / « - » | №л/л | Могу объяснить другому | разобрался | Нужно повторить | Требуется помощь | | 1 |
|
|
|
| | 2 |
|
|
|
| | 3 |
|
|
|
| | 4 |
|
|
|
| | 5 |
|
|
|
|
|
Стратегия «Джексо»
|