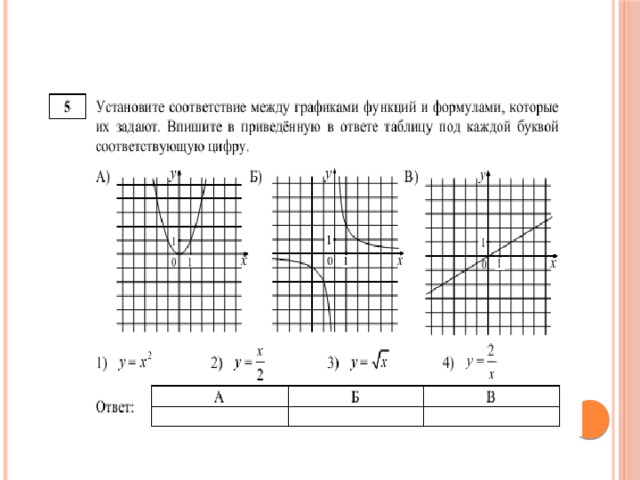
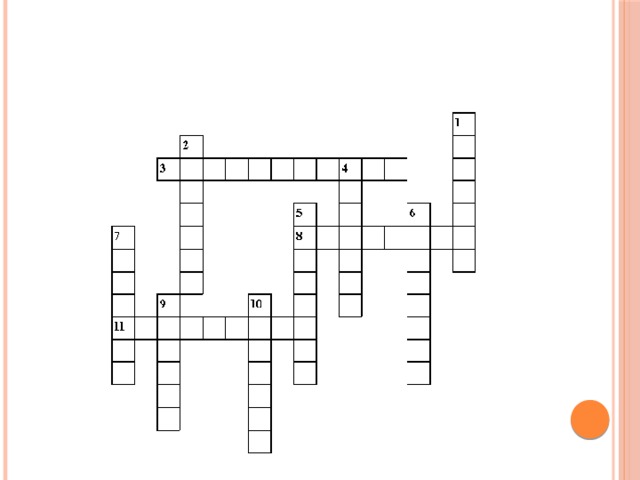
В данной презентации представлено формирование универсальных учебных действий на уроках математики в основной школе, которые могут быть использованы в учебном процессе. При изучении математики в школе в процессе вычислений, измерений, поиска решения задач и т. д.формируются основные мыслительные операции: анализ, синтез,сравнение, аналогия, объяснять этапы решения задачи. Таким образом происходит формирование универсальных учебных действий.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Универсальные учебные действия
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Универсальные учебные действия »
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
2100 руб.
3000 руб.
1970 руб.
2820 руб.
2020 руб.
2880 руб.
2020 руб.
2880 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства


 9 Б.2-6хВ.7-3х1)x2 2)x7 3)x-2 4)xВыполните взаимопроверку А Б В" width="640"
9 Б.2-6хВ.7-3х1)x2 2)x7 3)x-2 4)xВыполните взаимопроверку А Б В" width="640"
 b , то b Если a , a b , то a Если ab , то 3a3b Если ab , то −4a Если a , то a−3,7 Ответ _ " width="640"
b , то b Если a , a b , то a Если ab , то 3a3b Если ab , то −4a Если a , то a−3,7 Ответ _ " width="640"
 b, cd, то a+c(b+d)" width="640"
b, cd, то a+c(b+d)" width="640"