Решение задач С2

Решение задач С2

Презентация "Решение задач С2" показывает преимущество координатного метода.перед традиционным на примерах четырех задач из банка заданий ЕГЭ 2014 года.. Задачи представлены с решением, что позволяет быстро осуществить проверку на уроке.

Задачи для самостоятельного решения:

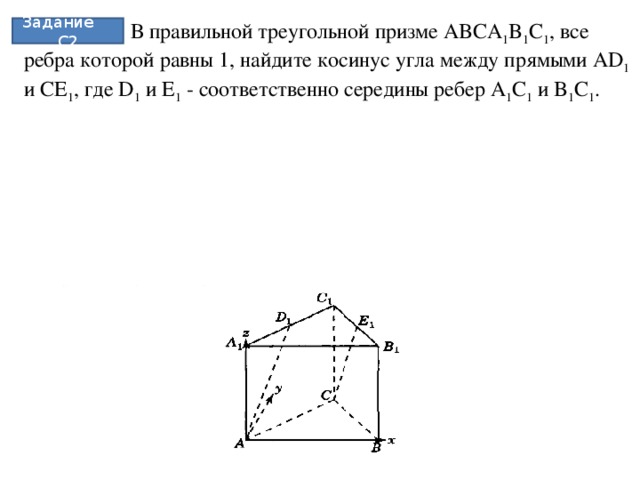
1. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите косинус угла между прямыми AD1 и CE1, где D1 и E1 - соответственно середины ребер A1C1 и B1C1.

2. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите косинус угла между прямыми AD1 и CE1, где D1 и E1 - соответственно середины ребер A1C1 и B1C1.

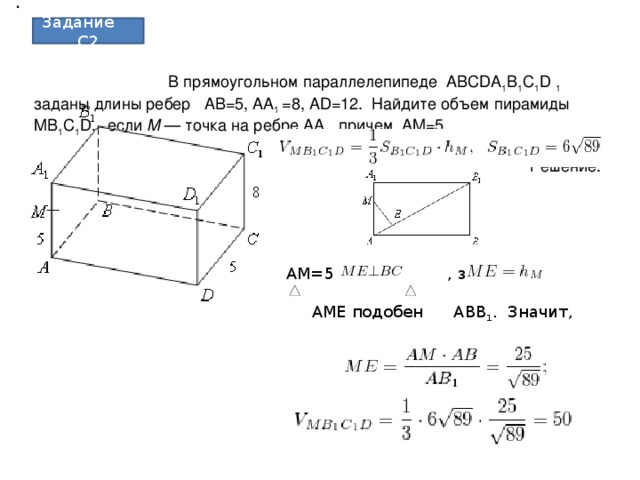
3. В прямоугольном параллелепипеде ABCDA1B1C1D 1 заданы длины ребер AB=5, AA1 =8, AD=12. Найдите объем пирамиды MB1C1D, если M — точка на ребре AA1, причем AM=5

Вы уже знаете о суперспособностях современного учителя?

Тратить минимум сил на подготовку и проведение уроков.

Быстро и объективно проверять знания учащихся.

Сделать изучение нового материала максимально понятным.

Избавить себя от подбора заданий и их проверки после уроков.

Наладить дисциплину на своих уроках.

Получить возможность работать творчески.

=> ПОЛУЧИТЬ СУПЕРСПОСОБНОСТИ УЧИТЕЛЯ <=

Просмотр содержимого документа
«Решение задач С2 »

Решение задач С2

Харитоненко Н.В.

МБОУ СОШ №3 с.Александров Гай

Задание С2

В правильной треугольной призме ABCA 1 B 1 C 1 , все ребра которой равны 1, найдите косинус угла между прямыми AD 1 и CE 1 , где D 1 и E 1 - соответственно середины ребер A 1 C 1 и B 1 C 1 .

Задание С2

В прямоугольном параллелепипеде ABCDA 1 B 1 C 1 D 1 заданы длины ребер AB=5, AA 1 =8, AD=12. Найдите объем пирамиды MB 1 C 1 D, если M — точка на ребре AA 1 , причем AM=5

Решение.

AM=5 и , значит

AME подобен ABB 1 . Значит,

Предмет: Математика

Категория: Презентации

Целевая аудитория: 11 класс

Скачать
Решение задач С2

Автор: Харитоненко Наталья Владимировна

Дата: 04.02.2015

Номер свидетельства: 167408

Похожие файлы

Пути и способы осуществления дифференциации обучения при формировании обобщенного приема решения задач

object(ArrayObject)#853 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(193) "Пути и способы осуществления дифференциации обучения при формировании обобщенного приема решения задач"
    ["seo_title"] => string(126) "puti-i-sposoby-osushchiestvlieniia-diffierientsiatsii-obuchieniia-pri-formirovanii-obobshchiennogho-priiema-rieshieniia-zadach"
    ["file_id"] => string(6) "314650"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(7) "prochee"
    ["date"] => string(10) "1459751208"
  }
}

Программа элективного курса "Решение задач с параметрами"

object(ArrayObject)#875 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(107) "Программа элективного курса "Решение задач с параметрами" "
    ["seo_title"] => string(64) "proghramma-eliektivnogho-kursa-rieshieniie-zadach-s-paramietrami"
    ["file_id"] => string(6) "157156"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(5) "uroki"
    ["date"] => string(10) "1421562791"
  }
}

конспек урока математики на тему "Решение задач на совместную работу"

object(ArrayObject)#853 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(129) "конспек урока математики на тему "Решение задач на  совместную работу" "
    ["seo_title"] => string(77) "konspiek-uroka-matiematiki-na-tiemu-rieshieniie-zadach-na-sovmiestnuiu-rabotu"
    ["file_id"] => string(6) "204440"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(5) "uroki"
    ["date"] => string(10) "1429647624"
  }
}

Программа спецкурса по математике «Решение задач повышенной сложности» (7 класс)

object(ArrayObject)#875 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(149) "Программа спецкурса по математике «Решение задач повышенной сложности» (7 класс) "
    ["seo_title"] => string(89) "proghramma-spietskursa-po-matiematikie-rieshieniie-zadach-povyshiennoi-slozhnosti-7-klass"
    ["file_id"] => string(6) "236084"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(12) "planirovanie"
    ["date"] => string(10) "1443957822"
  }
}

Решение задач на оптимизацию

object(ArrayObject)#853 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(53) "Решение задач на оптимизацию"
    ["seo_title"] => string(35) "rieshieniie-zadach-na-optimizatsiiu"
    ["file_id"] => string(6) "248687"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(5) "uroki"
    ["date"] => string(10) "1446750388"
  }
}

Просмотр содержимого документа «Решение задач С2 »

Похожие файлы

Полезное для учителя

Просмотр содержимого документа
«Решение задач С2 »