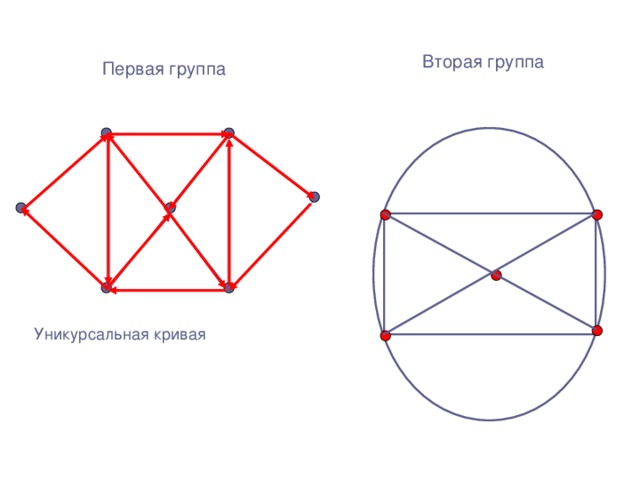
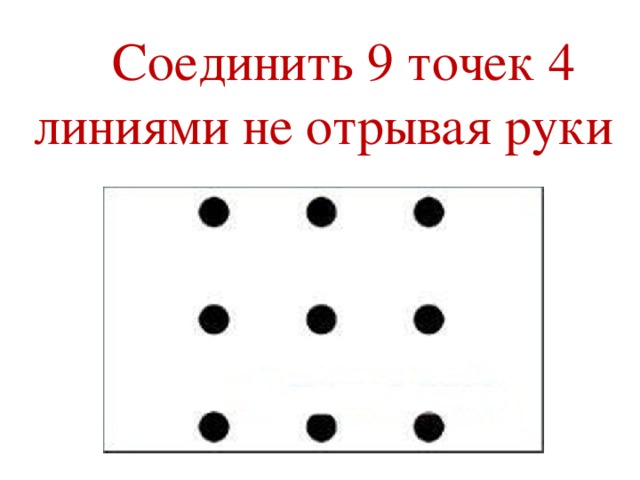
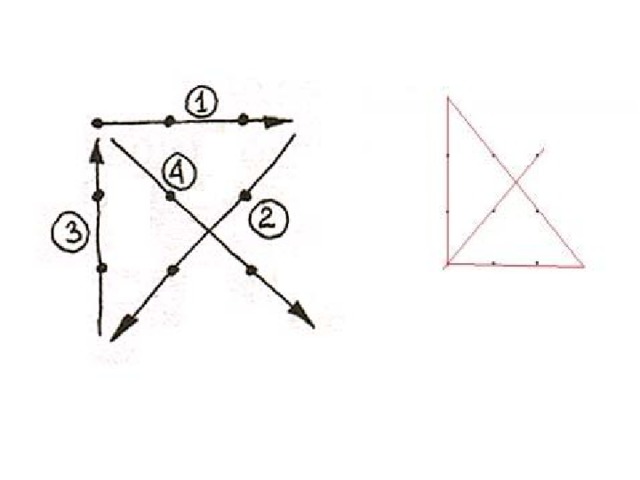
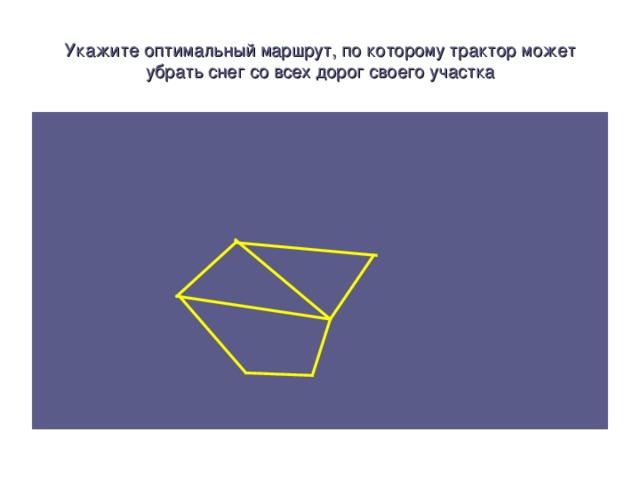
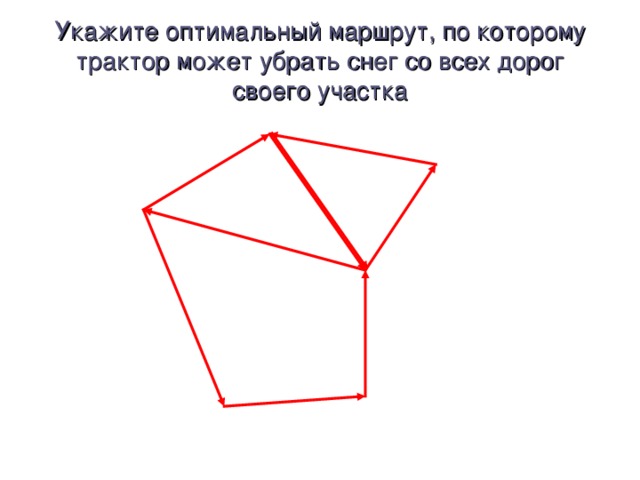
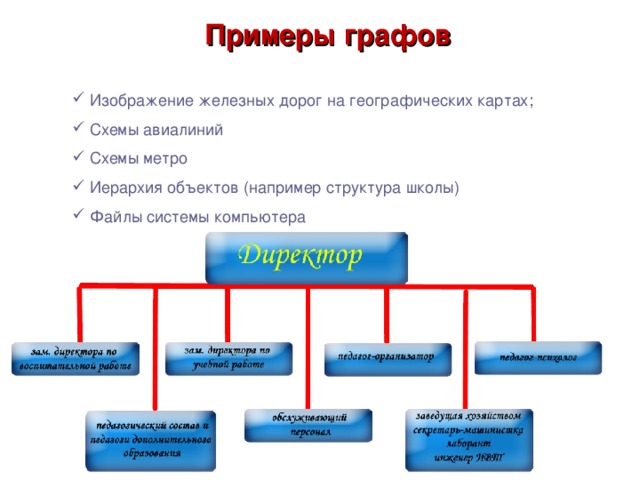
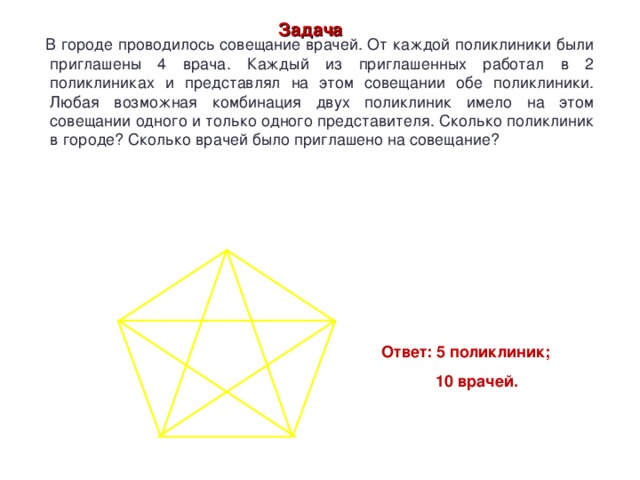
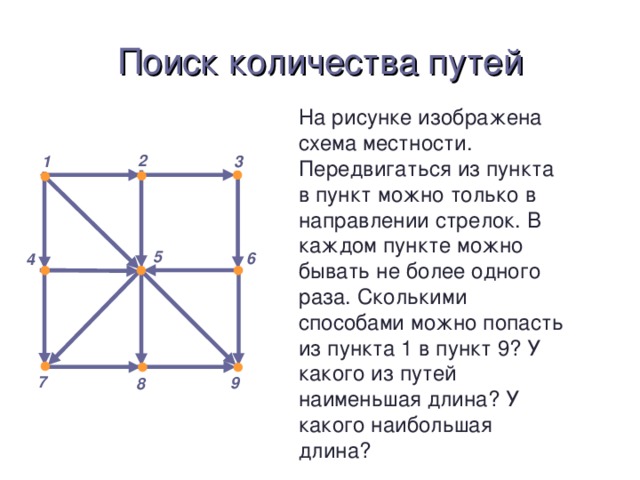
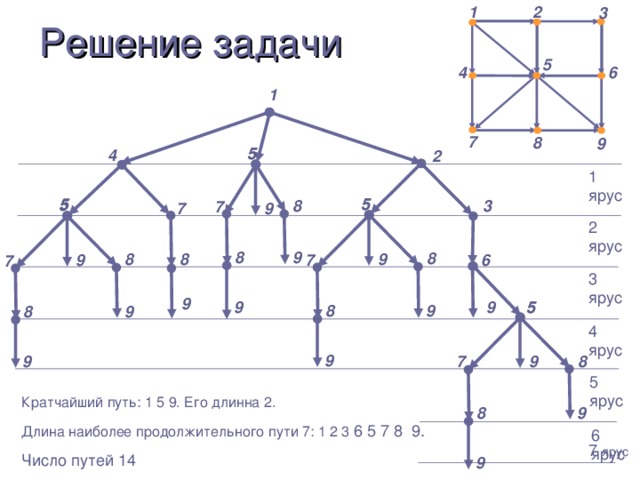
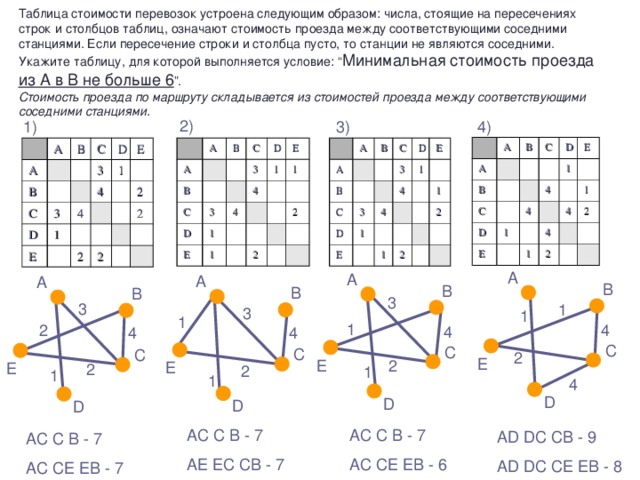
Понятие графа целесообразно вводить после того, как разобрано несколько задач, подобных задаче 1, решающее соображение в которых – графическое представление. Важно, чтобы ученики сразу осознали, что один и тот же граф может быть нарисован разными способами. Строгое определение графа, на мой взгляд, давать не нужно, т.к. оно слишком громоздко и это только затруднит обсуждение. На первых порах хватит и интуитивного понятия. При обсуждении понятия изоморфизма можно решить несколько упражнений на определение изоморфных и неизоморфных графов. Одно из центральных мест темы – теорема о четности числа нечетных вершин. Важно, чтобы ученики до конца разобрались в ее доказательстве и научились применять к решению задач. При разборе нескольких задач рекомендую не ссылаться на теорему, а фактически повторять ее доказательство. Чрезвычайно важно также понятие связности графа. Содержательным соображением здесь является рассмотрение компоненты связности, на это необходимо обратить особое внимание. Эйлеровы графы – тема почти игровая.
Создайте Ваш сайт учителя Курсы ПК и ППК Видеоуроки Олимпиады Вебинары для учителей
Применение теории графов к решению задач
Просмотр содержимого документа
«Применение теории графов к решению задач»
«Применение теории графов к решению задач»
Свойства графов
Решая задачу про Кенигсбергские мосты, Эйлер установил, в частности, следующие СВОЙСТВА графа:
- Если в фигуре только четные вершины , то ее можно нарисовать одним росчерком, независимо от того, с какого места начинается черчение.
2) Если в фигуре имеется только одна пара нечетных вершин, то такую фигуру можно нарисовать одним росчерком, начав черчение в одной из нечетных вершин.
3) Если фигура имеет более одной пары нечетных вершин, то она вовсе не может быть нарисована одним росчерком.
В задаче о семи Кенигсбергских мостах все четыре вершины соответствующего графа - нечетные, т.е. нельзя пройти по всем мостам ровно один раз и закончить путь там, где он был начат.
Свойства графов
Кроме трех свойств графа, которые установил Эйлер, решая задачу про Кенигсбергские мосты, он вывел еще два СВОЙСТВА :
4) Число нечетных вершин графа всегда четно.
5) Если в графе имеются нечетные вершины, то наименьшее число росчерков, которыми можно нарисовать граф, равно половине числа нечетных вершин этого графа.
Например, если фигура имеет четыре нечетные вершины, то ее можно начертить самое меньшее двумя росчерками.
Этот вопрос положил начало циклу новых увлекательных задач:
если дана геометрическая фигура, как начертить ее на бумаге одним росчерком пера , не проводя дважды ни одну линию?
Например: как проложить дорожки в дендропарке, чтобы посетители увидели все растения не проходя дважды по одной.
Вторая группа
Первая группа
Уникурсальная кривая
Соединить 9 точек 4 линиями не отрывая руки
Укажите оптимальный маршрут, по которому трактор может убрать снег со всех дорог своего участка
Укажите оптимальный маршрут, по которому трактор может убрать снег со всех дорог своего участка
Примеры графов
- Изображение железных дорог на географических картах;
- Схемы авиалиний
- Схемы метро
- Иерархия объектов (например структура школы)
- Файлы системы компьютера
Схема железнодорожных станций
Схема метро
Схема горнолыжных трасс
Географическая карта
Блок – схемы программ для ЭВМ
Схема авиалиний
Графы используются :
В строительстве
для составления чертежей;
для расчета материала;
для расчета количества рабочих;
для расчетов устойчивости откоса
В физике
Анализ электрических цепей распознаётся методом графов, также применяется в классической электродинамике СТО, энергетике, радиоэлектронике и др.
В химии
Используется для составления формул
Для исследования стационарной кинетически ферментативных реакций
Финансы и кредит
«Теория графов в управлении организационными системами»
Экология (геоботаника)
Метод графов при составлении дихотомических ключей для определения растений.
Транспорт
Для расчета пассажиропотока
Медицина
Исследование биоритмов
Биология
Для анализа биологических структур и генных систем
Спорт
Разработка стратегии игры
С помощью построения графа решается ряд задач входящих в ЕГЭ и ОГЭ:
Задача
В городе проводилось совещание врачей. От каждой поликлиники были приглашены 4 врача. Каждый из приглашенных работал в 2 поликлиниках и представлял на этом совещании обе поликлиники. Любая возможная комбинация двух поликлиник имело на этом совещании одного и только одного представителя. Сколько поликлиник в городе? Сколько врачей было приглашено на совещание?
Ответ: 5 поликлиник;
10 врачей.
Поиск количества путей
На рисунке изображена схема местности. Передвигаться из пункта в пункт можно только в направлении стрелок. В каждом пункте можно бывать не более одного раза. Сколькими способами можно попасть из пункта 1 в пункт 9? У какого из путей наименьшая длина? У какого наибольшая длина?
2
3
1
5
6
4
7
9
8
2
1
3
Решение задачи
5
6
4
1
7
8
9
5
5
4
2
1 ярус
5
5
5
5
8
3
7
7
9
2 ярус
8
9
8
9
8
8
6
9
7
7
3 ярус
9
9
5
9
5
9
8
9
8
4 ярус
9
8
9
9
7
5 ярус
Кратчайший путь: 1 5 9. Его длинна 2.
Длина наиболее продолжительного пути 7: 1 2 3 6 5 7 8 9.
Число путей 14
9
8
6 ярус
7 ярус
9
Проблема трех домов и трех колодцев
Три соседа имеют три общих колодца. Можно ли провести непересекающиеся дорожки от каждого дома к каждому колодцу? Дорожки не могут проходить через колодцы и домики.
Два игрока играют в следующую игру. Перед ними лежат две кучки камней, в первой из которых 3, а во второй – 2 камня. У каждого игрока неограниченно много камней. Игроки ходят по очереди. Ход состоит в том, что игрок или увеличивает в 3 раза число камней в какой-то куче, или добавляет 1 камень в какую-то кучу. Выигрывает игрок, после хода которого общее число камней в двух кучах становится не менее 16 камней. Кто выигрывает при безошибочной игре – игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте.
3,2, ∑ 5
1 ход
1 игрок
3,6, ∑ 9
9,2, ∑ 11
3,3, ∑ 6
3,3, ∑ 6
4,2, ∑ 6
2 ход
2 игрок
3,4, ∑ 7
3,9, ∑ 12
12,2 , ∑ 14
3,18, ∑ 21
5,2, ∑ 7
4,3, ∑ 7
27,2, ∑ 29
4,6, ∑ 10
Правильное указание выигрывающего игрока и его ходов со строгим доказательством правильности (с помощью дерева игры)
Оценивается максимальным кол-вом баллов.
Выигрывает второй игрок.
Для доказательства рассмотрим неполное дерево игры
Числа соответствуют количеству камней на каждом этапе игры, в первой и второй кучах соответственно и их сумма.
Второй игрок выигрывает на четвертом ходу, после любого ответа первого игрока.
Дерево содержит все возможные варианты ходов первого игрока. Из него видно,
что при любом ходе первого игрока у второго имеется ход, приводящий к победе.
3 ход
1 игрок
12,3, ∑ 15
4,9, ∑ 13
5,3, ∑ 8
4,4, ∑ 8
4 ход
2 игрок
36,3, ∑ 39
15,3, ∑ 18
4,27, ∑ 31
12,9, ∑ 21
13,3, ∑ 16
12,9, ∑21
12,4, ∑ 16
12,4, ∑ 16
24
Таблица стоимости перевозок устроена следующим образом: числа, стоящие на пересечениях строк и столбцов таблиц, означают стоимость проезда между соответствующими соседними станциями. Если пересечение строки и столбца пусто, то станции не являются соседними.
Укажите таблицу, для которой выполняется условие: “ Минимальная стоимость проезда
из А в B не больше 6 ”.
Стоимость проезда по маршруту складывается из стоимостей проезда между соответствующими соседними станциями.
2)
1)
3)
4)
A
A
B
B
C
C
D
D
4
4
1
1
Е
Е
4
1
4
1
2
2
A
A
A
A
A
A
B
B
B
B
B
B
C
C
C
C
C
C
3
3
3
3
3
3
D
D
D
D
D
D
1
Е
1
4
4
Е
Е
1
4
Е
1
4
4
Е
4
Е
1
1
1
1
1
2
2
1
2
2
2
2
2
2
A
A
A
A
B
B
B
B
3
3
1
3
1
1
1
2
4
4
4
4
C
C
C
C
2
E
E
2
E
E
2
2
1
1
1
4
D
D
D
D
AC C B - 7
AC CE EB - 6
AC C B - 7
AE EC CB - 7
AD DC CB - 9
AD DC CE EB - 8
AC C B - 7
AC CE EB - 7
Рефлексия
Выберите ответ:
1. На занятии я узнал что-то новое да нет
2. На занятии мне понравилось:
история графов практические задания
3. Я применю это в своей практике да нет
Полезное для учителя
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт