Презентация разработана к проекту "Решение уравнений и неравенств с параметрами". Способствует лучшему усвоению темы.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Презентация "Решение уравнений и неравенств с параметрами"
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Презентация "Решение уравнений и неравенств с параметрами"»
Полезное для учителя
Распродажа видеоуроков!
1630 руб.
2330 руб.
2220 руб.
3170 руб.
2020 руб.
2880 руб.
1790 руб.
2560 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства





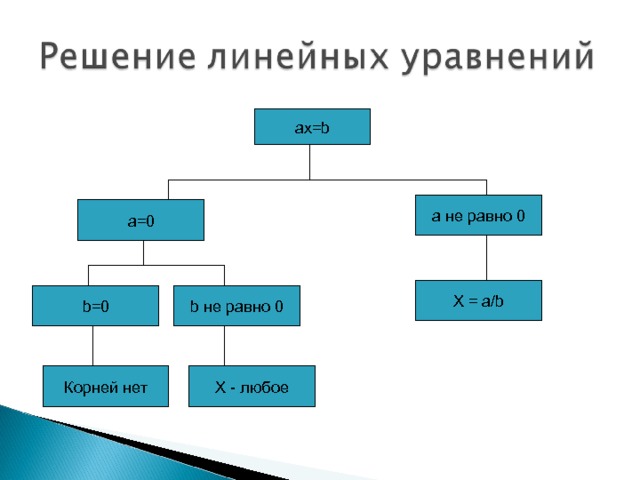




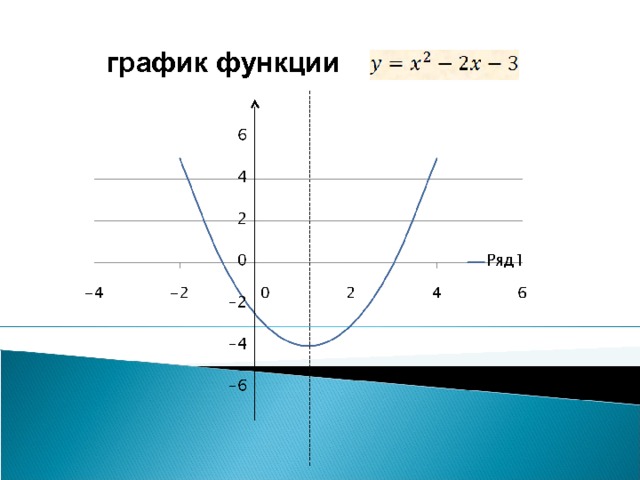
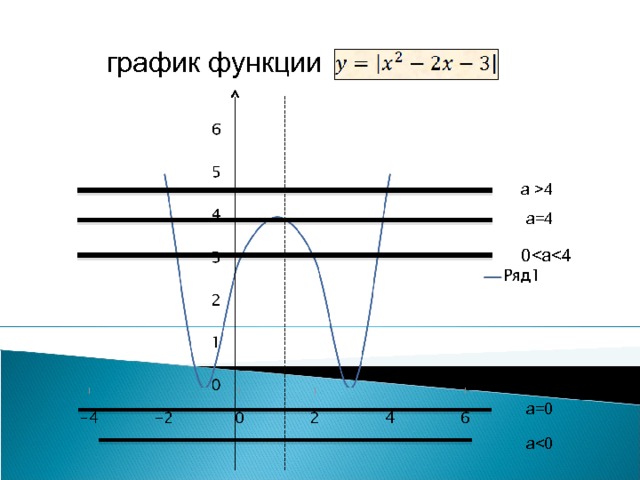 4 а=4 0 a=0 a" width="640"
4 а=4 0 a=0 a" width="640"
 4 - два решения При 0 При а=4 три решения (x=1+2 , x=1-2 , x = 1 ) " width="640"
4 - два решения При 0 При а=4 три решения (x=1+2 , x=1-2 , x = 1 ) " width="640"
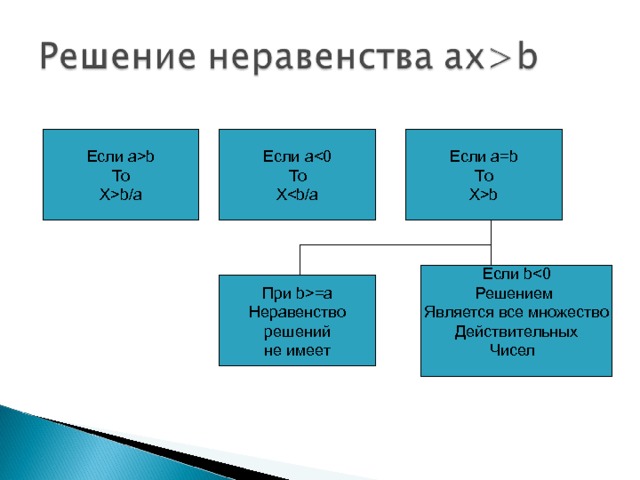 b Если ab То Xb/a Если aТо XЕсли bРешением Является все множество Действительных Чисел При b=a Неравенство решений не имеет " width="640"
b Если ab То Xb/a Если aТо XЕсли bРешением Является все множество Действительных Чисел При b=a Неравенство решений не имеет " width="640"

 2(x-1) Решение : x-2x-2-1 (m-2)x-3 Данное неравенство является линейным, поэтому контрольным значением для него будет m-2=0 Далее имеем : При m-20. то есть m2 , x-3/(m-2) , x3/(2-m) При m-2При m=2 неравенство принимает вид 0 x-3. Здесь x- любое действительное число. Ответ: при m2 x3/(2-m); при mпри m=2 x- любое действительное число " width="640"
2(x-1) Решение : x-2x-2-1 (m-2)x-3 Данное неравенство является линейным, поэтому контрольным значением для него будет m-2=0 Далее имеем : При m-20. то есть m2 , x-3/(m-2) , x3/(2-m) При m-2При m=2 неравенство принимает вид 0 x-3. Здесь x- любое действительное число. Ответ: при m2 x3/(2-m); при mпри m=2 x- любое действительное число " width="640"

















