Ниже приведенный урок был проведен в 10 классе МБОУ города Костромы "В(с) ОШ №2" учительницей математики Сергеевой Е. Н.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
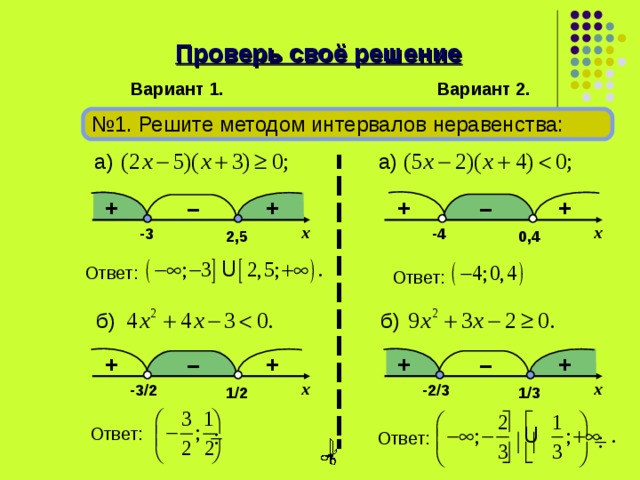
Презентация к уроку: "Решение квадратных неравенств методом интервалов"
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Презентация к уроку: "Решение квадратных неравенств методом интервалов"»
Полезное для учителя
Распродажа видеоуроков!
2100 руб.
3000 руб.
1970 руб.
2820 руб.
1740 руб.
2480 руб.
2000 руб.
2860 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства



 0 при a 0 D 0 D = 0 D (-∞; х 1 ) U (х 2 ; ∞) (-∞; х 1 ) U (х 2 ; ∞) (-∞; ∞) a (х 1 ; х 2 ) Решений нет Решений нет" width="640"
0 при a 0 D 0 D = 0 D (-∞; х 1 ) U (х 2 ; ∞) (-∞; х 1 ) U (х 2 ; ∞) (-∞; ∞) a (х 1 ; х 2 ) Решений нет Решений нет" width="640"
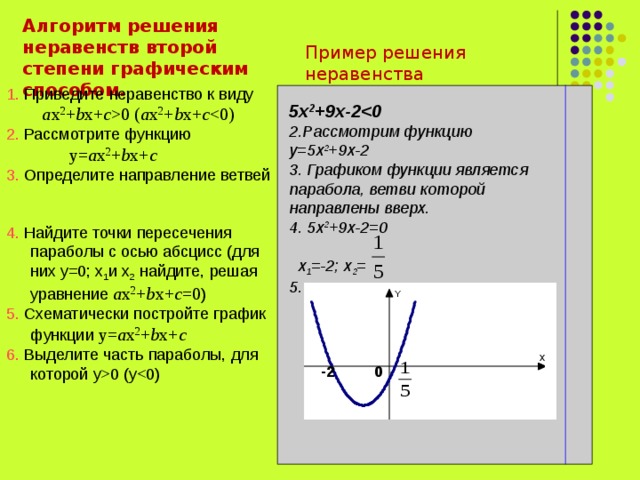 0 ( a x 2 + b x+ c 2. Рассмотрите функцию y= a x 2 + b x+ c 3 . Определите направление ветвей 4. Найдите точки пересечения параболы с осью абсцисс (для них y=0 ; х 1 и х 2 найдите, решая уравнение a x 2 + b x+ c =0 ) 5. Схематически постройте график функции y= a x 2 + b x+ c 6. Выделите часть параболы, для которой y0 (y5х 2 +9х-2 2 . Рассмотрим функцию y= 5х 2 +9х-2 3 . Графиком функции является парабола, ветви которой направлены вверх. 4. 5х 2 +9х-2= 0 х 1 =-2; х 2 = 5. 0 -2" width="640"
0 ( a x 2 + b x+ c 2. Рассмотрите функцию y= a x 2 + b x+ c 3 . Определите направление ветвей 4. Найдите точки пересечения параболы с осью абсцисс (для них y=0 ; х 1 и х 2 найдите, решая уравнение a x 2 + b x+ c =0 ) 5. Схематически постройте график функции y= a x 2 + b x+ c 6. Выделите часть параболы, для которой y0 (y5х 2 +9х-2 2 . Рассмотрим функцию y= 5х 2 +9х-2 3 . Графиком функции является парабола, ветви которой направлены вверх. 4. 5х 2 +9х-2= 0 х 1 =-2; х 2 = 5. 0 -2" width="640"

 0 . 2 . Отметить нули функции на координатной прямой пустыми (если неравенство строгое) или сплошными (если неравенство не строгое) точками. 3. Определить знак функции на каждом промежутке (а для квадратичной функции достаточно определить знак лишь в одном из промежутков, так как знаки будут чередоваться потому, что функция непрерывна на всей области определения). 4. а) Выделить те промежутки, где q(x) 0 . б) Выделить те промежутки, где q(x) ." width="640"
0 . 2 . Отметить нули функции на координатной прямой пустыми (если неравенство строгое) или сплошными (если неравенство не строгое) точками. 3. Определить знак функции на каждом промежутке (а для квадратичной функции достаточно определить знак лишь в одном из промежутков, так как знаки будут чередоваться потому, что функция непрерывна на всей области определения). 4. а) Выделить те промежутки, где q(x) 0 . б) Выделить те промежутки, где q(x) ." width="640"