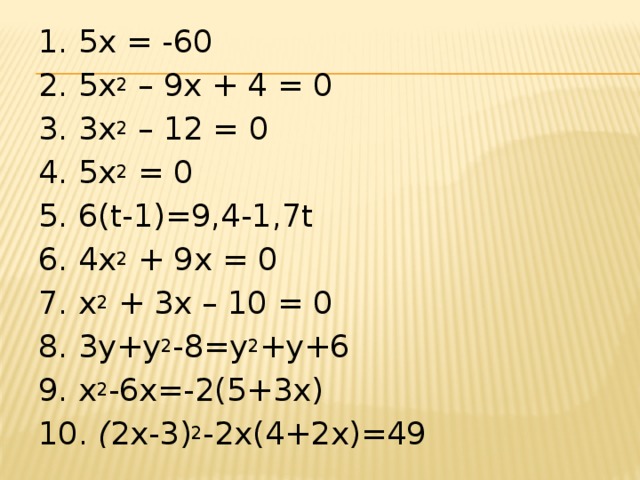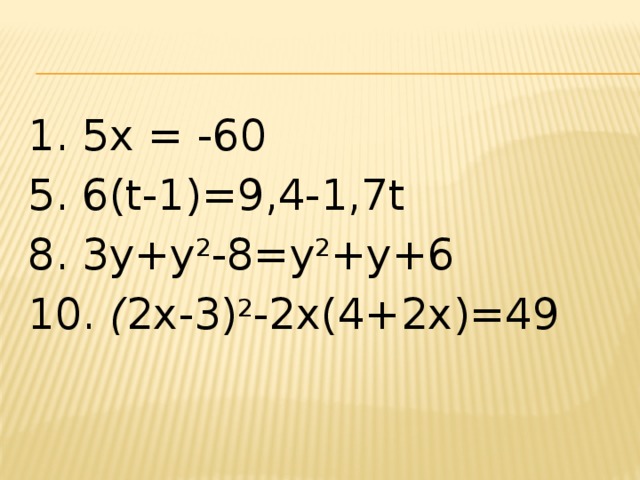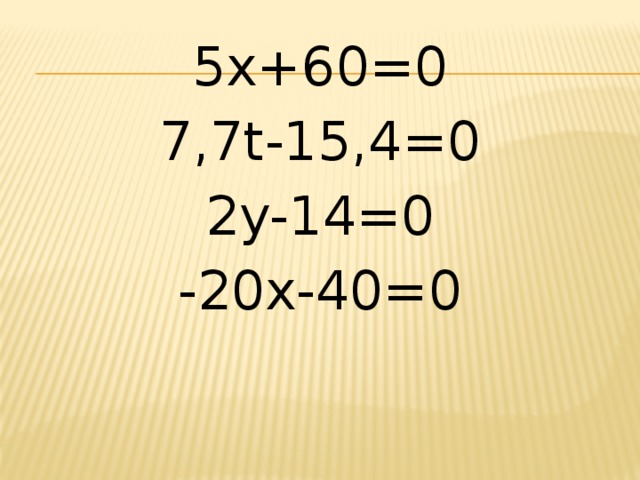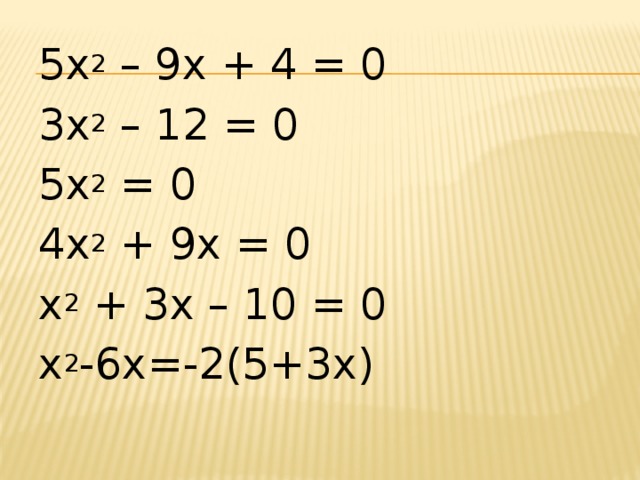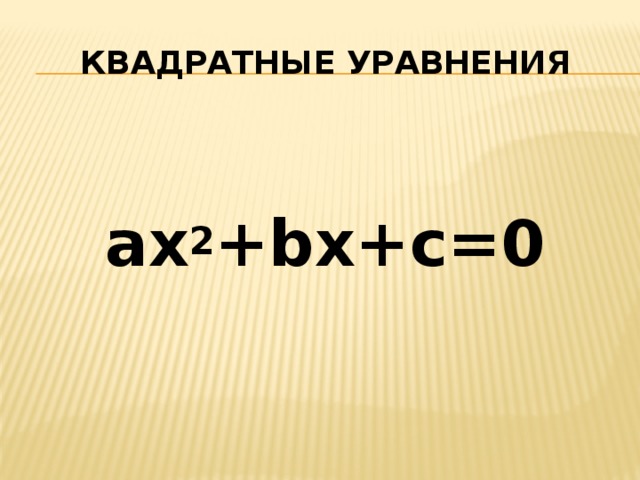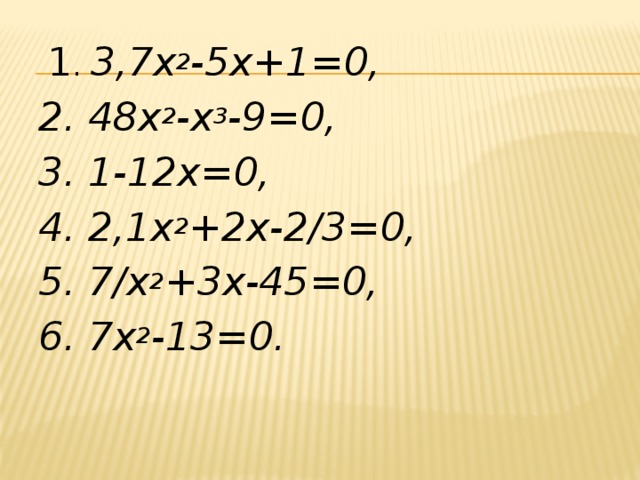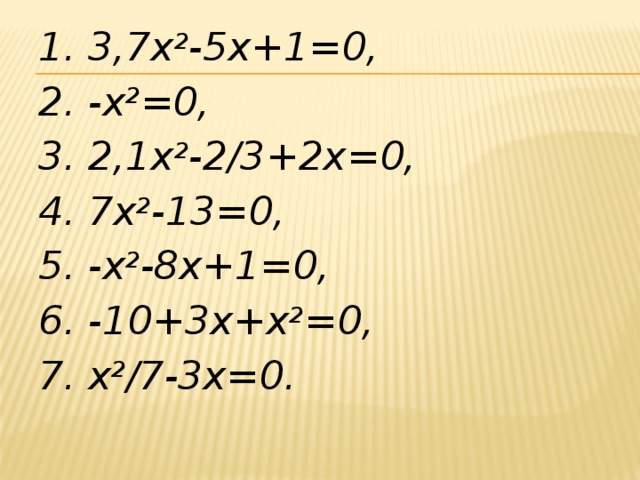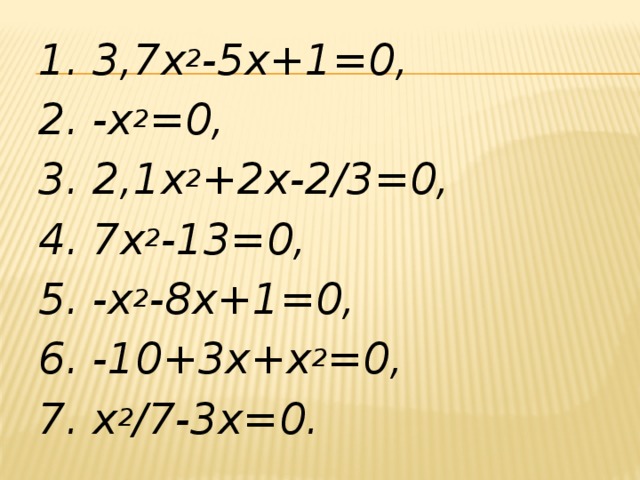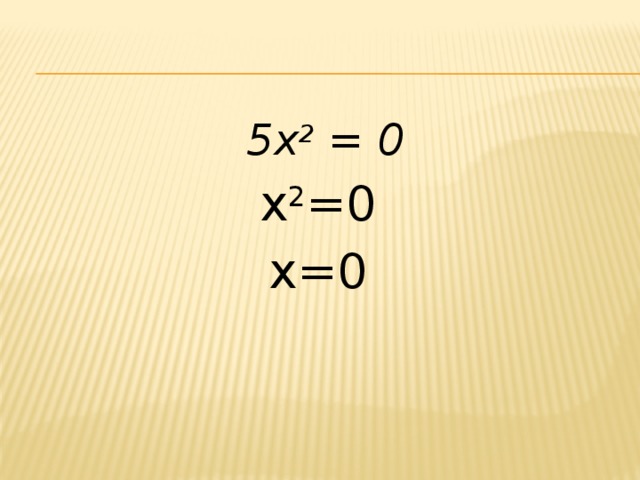Создайте Ваш сайт учителя Курсы ПК и ППК Видеоуроки Олимпиады Вебинары для учителей
Тип урока: Урок усвоения новых знаний
Цель урока: учащиеся научатся определять квадратные уравнения и отличать полные квадратные уравнения от неполных и получат возможность определять вид неполного квадратного уравнения и выбирать алгоритм его решения, а также самостоятельно анализировать условия достижения цели на основе учета выделенных учителем ориентиров действия в новом учебном материале.
1. 5x = -60
2. 5x 2 – 9x + 4 = 0
3. 3х 2 – 12 = 0
4. 5x 2 = 0
5. 6(t-1)=9,4-1,7t
6. 4х 2 + 9х = 0
7. x 2 + 3x – 10 = 0
8. 3y+y 2 -8=y 2 +y+6
9. х 2 -6х=-2(5+3х)
10. ( 2х-3) 2 -2х(4+2х)=49
1. 5x = -60
5. 6(t-1)=9,4-1,7t
8. 3y+y 2 -8=y 2 +y+6
10. ( 2х-3) 2 -2х(4+2х)=49
Линейные уравнения
ах+b=0
5х+60=0
7,7t-15,4=0
2y-14=0
-20х-40=0
Тема нашего урока :
"Определение квадратного уравнения. Неполные квадратные уравнения"
Цели урока:
1) выучить определение квадратного уравнения,
2) научиться определять по виду уравнения является ли оно квадратным или нет,
3) научиться определять вид квадратного уравнения - полное оно или неполное,
4) научиться выбирать нужный алгоритм решения неполного квадратного уравнения.
5x 2 – 9x + 4 = 0
3х 2 – 12 = 0
5x 2 = 0
4х 2 + 9х = 0
x 2 + 3x – 10 = 0
х 2 -6х=-2(5+3х)
Квадратные уравнения
ax 2 +bx+c=0
Определение квадратного уравнения
Это уравнение вида ax 2 +bx+c=0, где:
1) х - ………….. ,
2) a, b, c - ………….,
3) а ………….. .
Определение квадратного уравнения
Это уравнение вида ax 2 +bx+c=0, где:
1) х - переменная,
2) a, b, c – некоторые числа ,
3) а 0.
1 . 3,7х 2 -5х+1=0,
2. 48х 2 -х 3 -9=0,
3. 1-12х=0,
4. 2,1х 2 +2х-2/3=0,
5. 7/х 2 +3х-45=0,
6. 7х 2 -13=0.
1. 3,7х 2 -5х+1=0,
2. -х 2 =0,
3. 2,1х 2 -2/3+2х=0,
4. 7х 2 -13=0,
5. -х 2 -8х+1=0,
6. -10+3х+х 2 =0,
7. х 2 /7-3х=0.
1. a =3,7 b =5 c=1
2. a =-1 b =0 c=0
3. a =2,1 b =2 c=- 2/3
4. a =7 b =0 c=13
5. a =-1 b =-8 c=1
6. a =1 b =3 c=-10
7. a =1/7 b =-3 c=0
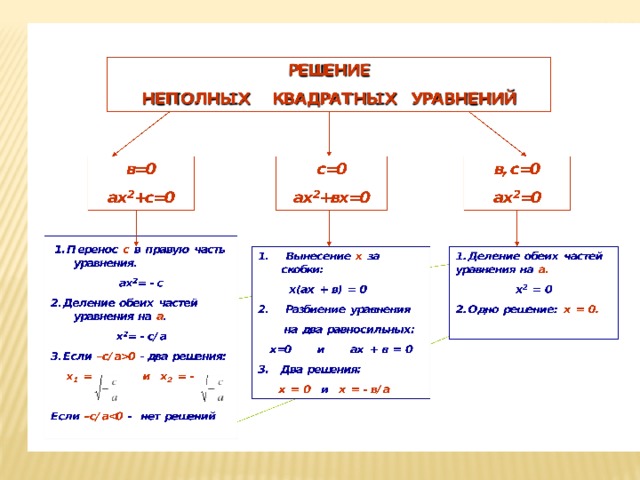
Определение неполного квадратного уравнения
Называется уравнение, если в нем хотя бы один из коэффициентов b или c равен нулю.
Неполные квадратные уравнения бывают трёх видов:
1) , где с 0
2) , где b 0
3) ,где с=0 и b=0
Неполные квадратные уравнения бывают трёх видов:
1) ax 2 +c=0, где с 0
2) ax 2 +bx=0, где b 0
3) ax 2 =0,где с=0 и b=0
1. 3,7х 2 -5х+1=0,
2. -х 2 =0,
3. 2,1х 2 +2х-2/3=0,
4. 7х 2 -13=0,
5. -х 2 -8х+1=0,
6. -10+3х+х 2 =0,
7. х 2 /7-3х=0.
I вид:
ax 2 +c=0, где с 0
Переносят свободный член в правую часть и делят обе части уравнения на a.
Решим неполные квадратные уравнения:
3х 2 – 12 = 0
3х 2 = 12
х 2 -6х=-2(5+3х)
х 2 +10=0
х 2 = 4
Х= 2
х 2 =-10
Х= -2
II вид:
ax 2 +bx=0, где b 0
Алгоритм решения неполного квадратного уравнения ax 2 +bx=0, где b 0 :
1)разложить левую часть на множители,
2) используя условие равенства произведения нулю, уравнение заменяется на два уравнения,
3) решается каждое,
4) записывается ответ.
I - 515(а)
Ответ: x=3/2;
II - 515(д)
Ответ: нет корней.
x= -3/2.
I - 517(а)
Ответ: x=4/3.
I - 517(б)
Ответ: x=6/5.
III вид:
ax 2 =0, с=0 и b=0.
Алгоритм решения неполного квадратного уравнения: ax 2 =0, с=0 и b=0
1) разделим обе части на а 0,
2) х 2 =0, х=0,
3) записать ответ.
5x 2 = 0
х 2 =0
х=0
СИНКВЕЙН «Квадратные уравнения»
- Название
- Описание (2 прилагательных)
- Действие (3 глагола)
- Чувство (фраза)
- Повторение сути (синоним названия)
Домашняя работа:
П 21; №№ 518; 519.
Спасибо всем за внимание!
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
