Создайте Ваш сайт учителя Курсы ПК и ППК Видеоуроки Олимпиады Вебинары для учителей
В презентации приводится построение тригонометрических функции, тригонометрические функции числового аргумента,построение функции графика вида,примеры. Презентация состоит из 27 слайдов. В каждом слайде подробно показаны графики и примеры.Построение графика функции y = sin x.,
Преобразование: y= sin(x)+m
Сдвиг у= sin(x) по оси y вверх, если m> 0
Построение графиков тригонометрических функций в 11классе
y
Учитель математики первой квалификационной категории МАОУ «Гимназия №37» г.Казань
Спиридонова Л.В.
x
С О Д Е Р Ж А Н И Е
Тригонометрические функции числового аргумента.
y=sin(x)
y=cos(x)
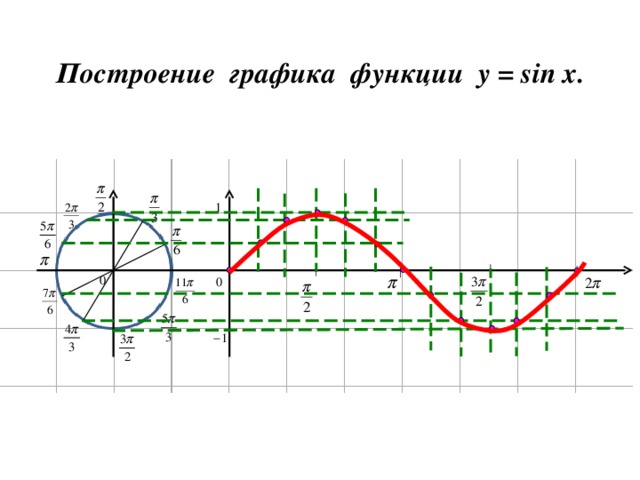
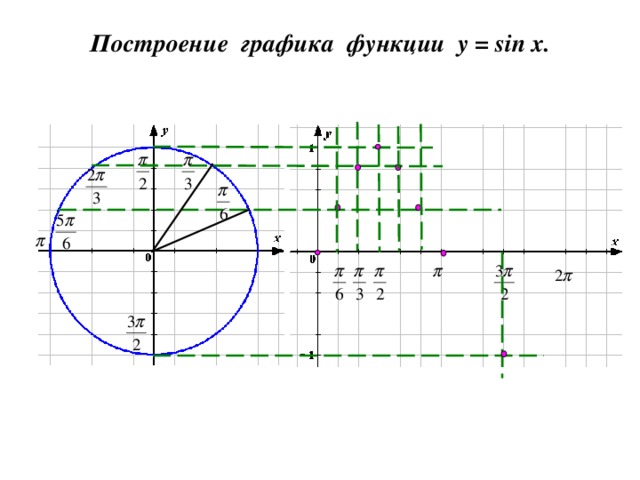
Построение графика функции y = sin x .
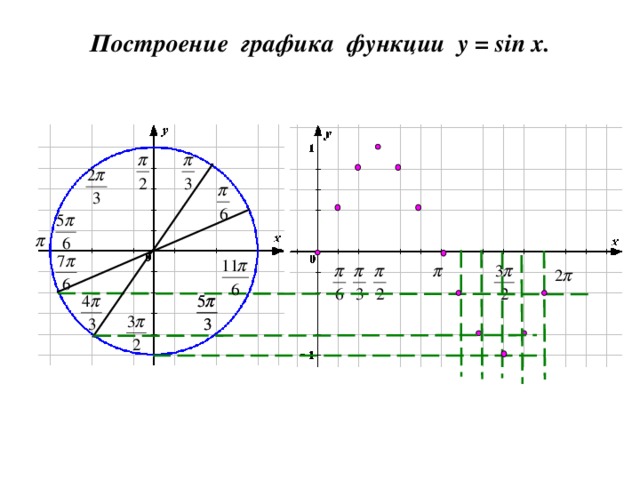
Построение графика функции y = sin x .
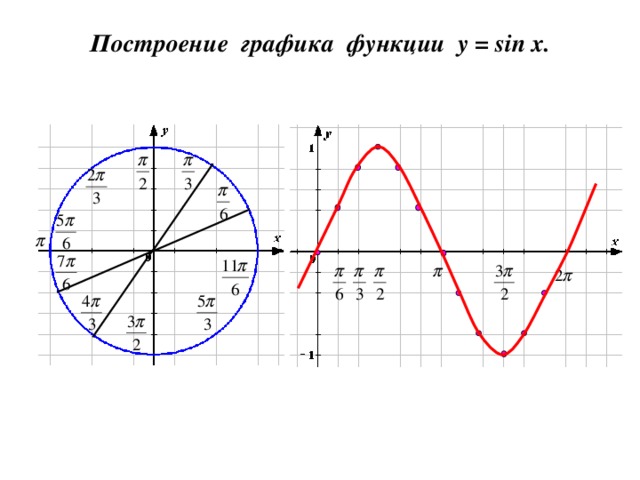
Построение графика функции y = sin x .
Построение графика функции y = sin x .
![Свойства функции у = sin ( x ) . 1. Областью определения функции является множество всех действительных чисел ( R ) 2. Областью изменений (Областью значений) ,E(y)= [ - 1; 1 ] . 3. Функция у = sin ( x) нечетная, т.к. sin (- x ) = - sin x Функция периодическая, с главным периодом 2 π . sin (x + 2 π ) = sin(x). 5. Функция непрерывная Убывает: [ π /2; 3 π /2 ] . 6. Возрастает: [ - π /2; π /2 ] . + + + - - -](https://fsd.kopilkaurokov.ru/uploads/user_file_551d45610ceeb/img_user_file_551d45610ceeb_7.jpg)
Свойства функции у = sin ( x ) .
1. Областью определения функции является множество
всех действительных чисел ( R )
2. Областью изменений (Областью значений) ,E(y)= [ - 1; 1 ] .
3. Функция у = sin ( x) нечетная, т.к. sin (- x ) = - sin x
sin (x + 2 π ) = sin(x).
5. Функция непрерывная
Убывает: [ π /2; 3 π /2 ] .
6. Возрастает: [ - π /2; π /2 ] .
+
+
+
-
-
-
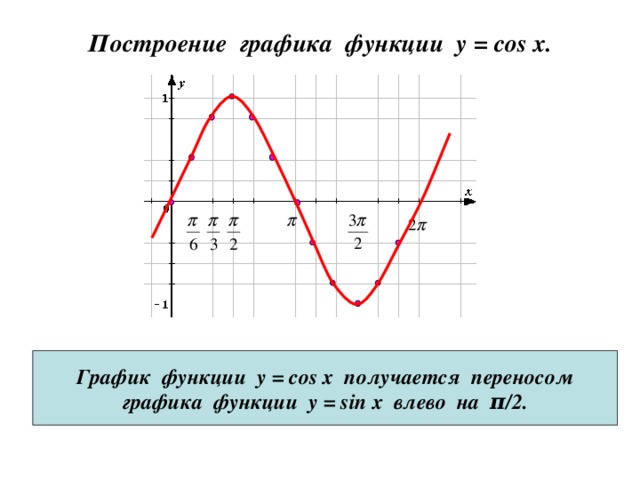
Построение графика функции y = cos x .
График функции у = cos x получается переносом
графика функции у = sin x влево на π /2.
![Свойства функции у = со s ( x ) . 1. Областью определения функции является множество всех действительных чисел ( R ) 2. Областью изменений (Областью значений),Е(у)= [ - 1; 1 ] . 3. Функция у = cos (х) четная, т.к. cos (- х ) = cos (х) Функция периодическая, с главным периодом 2 π . cos ( х + 2 π ) = cos (х) . 5. Функция непрерывная Убывает: [ 0 ; π ] . 6. Возрастает: [ π ; 2 π ] . + + + + - - -](https://fsd.kopilkaurokov.ru/uploads/user_file_551d45610ceeb/img_user_file_551d45610ceeb_9.jpg)
Свойства функции у = со s ( x ) .
1. Областью определения функции является множество
всех действительных чисел ( R )
2. Областью изменений (Областью значений),Е(у)= [ - 1; 1 ] .
3. Функция у = cos (х) четная, т.к. cos (- х ) = cos (х)
cos ( х + 2 π ) = cos (х) .
5. Функция непрерывная
Убывает: [ 0 ; π ] .
6. Возрастает: [ π ; 2 π ] .
+
+
+
+
-
-
-
Построение
графиков функций вида
у = sin ( x ) + m
и
у = cos (х) + m.
0 , или вниз, если m ." width="640"
Параллельный перенос графика вдоль оси Оу
График функции y=f(x) + m получается параллельным переносом графика функции y=f(x) , вверх на m единиц, если m 0 ,
или вниз, если m .
0 y m 1 x" width="640"
-1
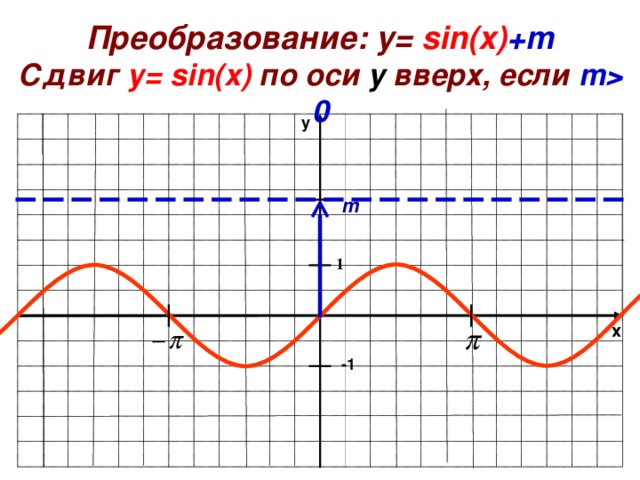
Преобразование: y= sin ( x ) +m
Сдвиг у= sin ( x ) по оси y вверх, если m 0
y
m
1
x
0 y m 1 x" width="640"
-1
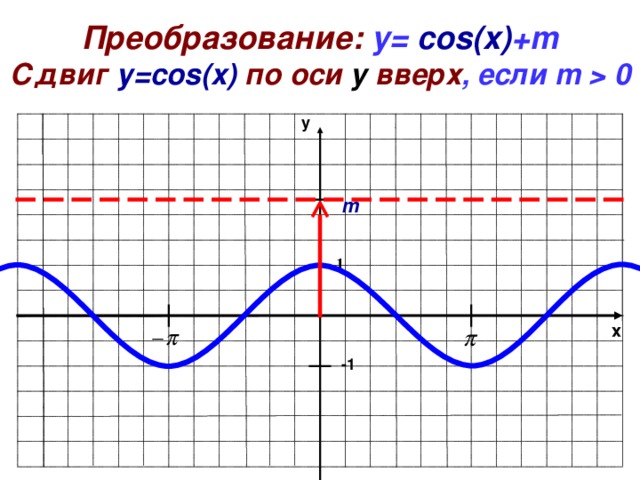
Преобразование: y= cos ( x ) +m
Сдвиг у= cos ( x ) по оси y вверх , если m 0
y
m
1
x
-1
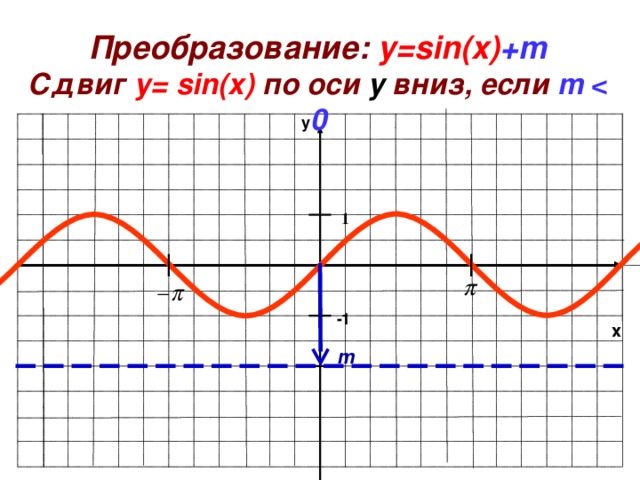
Преобразование: y=sin ( x ) +m
Сдвиг у= sin ( x ) по оси y вниз, если m 0
y
1
x
m
-1
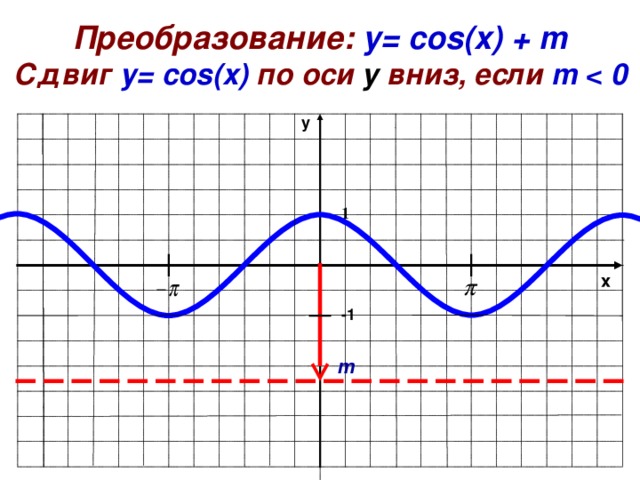
Преобразование: y= cos ( x ) + m
Сдвиг у= cos ( x ) по оси y вниз, если m 0
y
1
x
m
Построение
графиков функций вида
у = sin ( x + t )
и
у = cos ( х + t )
0 и вправо , если t 0." width="640"
Параллельный перенос графика вдоль оси Ох
График функции y = f(x + t) получается параллельным переносом графика функции y=f(x) по оси х на |t| единиц масштаба влево, если t 0
и вправо , если t 0.
0 y 1 x t" width="640"
-1
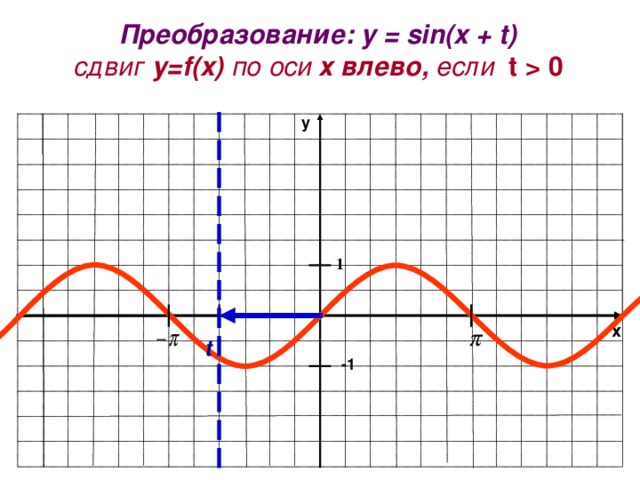
Преобразование: y = sin(x + t)
сдвиг у= f(x) по оси х влево, если t 0
y
1
x
t
0 y 1 x t" width="640"
-1
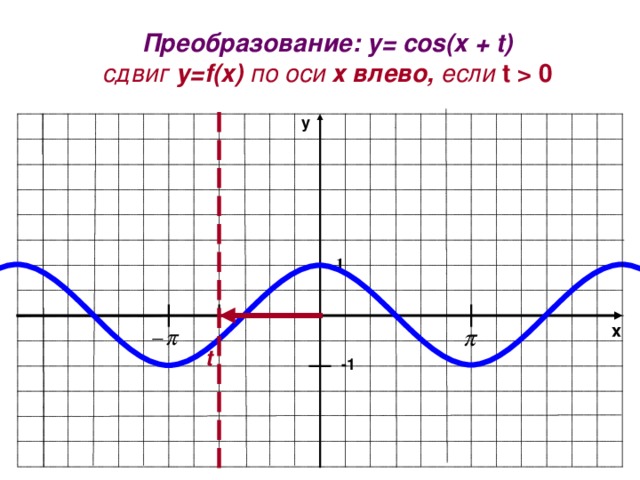
Преобразование: y= cos(x + t)
сдвиг у= f(x) по оси х влево, если t 0
y
1
x
t
-1
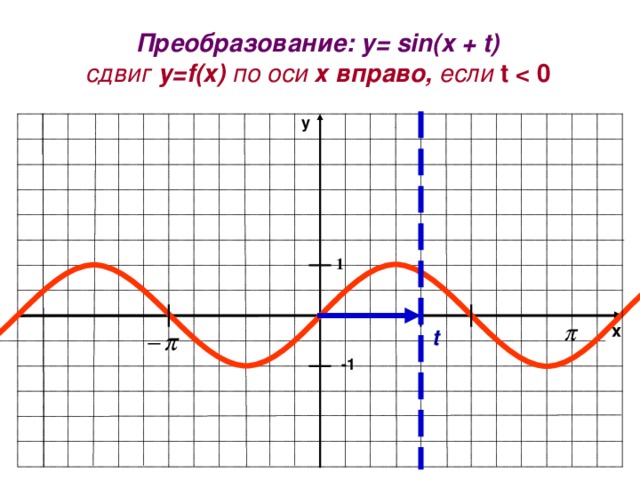
Преобразование: y= sin(x + t)
сдвиг у= f(x) по оси х вправо, если t 0
y
1
x
t
-1
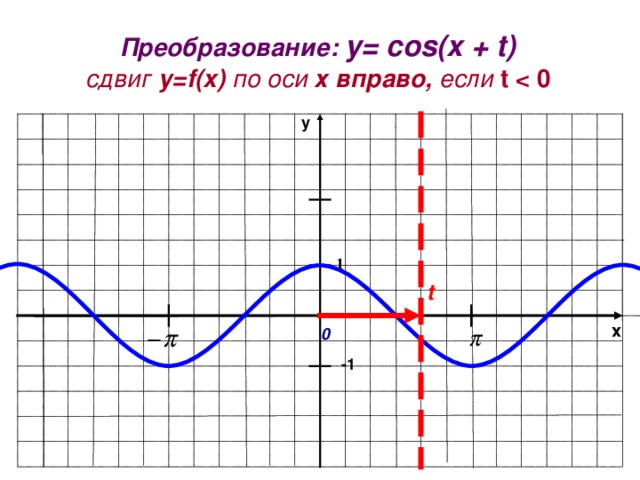
Преобразование: y= cos(x + t)
сдвиг у= f(x) по оси х вправо, если t 0
y
1
t
x
0
1 и 0 а 1" width="640"
Построение графиков функций вида у = А · sin ( x ) и y = А · cos ( x ) , при а 1 и 0 а 1
1 и сжатием к оси Ох с коэффициентом 0 А ." width="640"
Сжатие и растяжение вдоль оси Ох
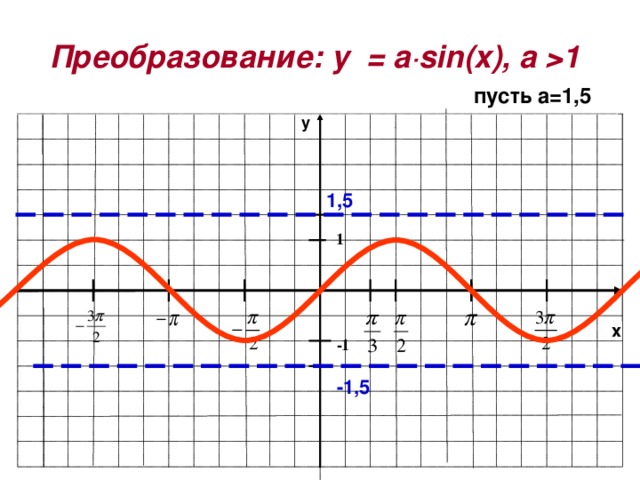
График функции у=А · f(x ) получаем растяжением графика функции у= f(x) с коэффициентом А вдоль оси Ох,если А 1 и сжатием к оси Ох с коэффициентом 0 А .
1 пусть а=1,5 y 1 x -1" width="640"
1,5
-1,5
Преобразование: y = a·sin ( x ), a 1
пусть а=1,5
y
1
x
-1
1 пусть а=1,5 y 1 x" width="640"
-1
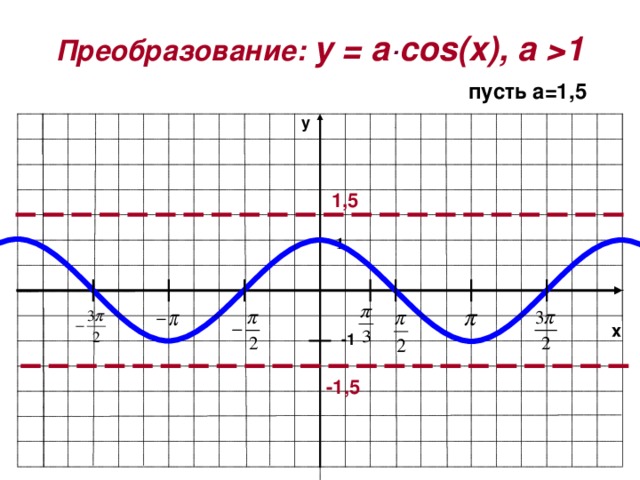
-1,5
1,5
Преобразование: y = a · cos ( x ), a 1
пусть а=1,5
y
1
x
-1
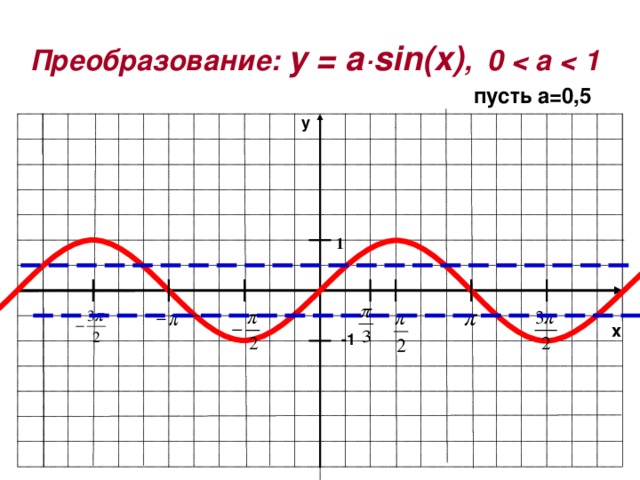
Преобразование: y = a·sin ( x ) , 0
пусть а=0,5
y
1
x
-1
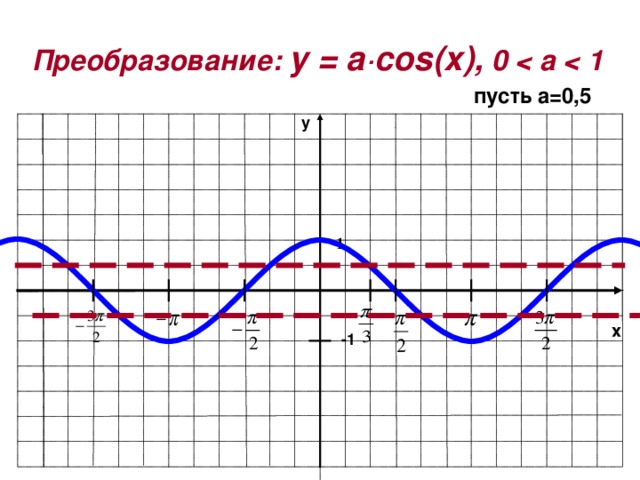
Преобразование: y = a·cos ( x ), 0
пусть а=0,5
y
1
x
y
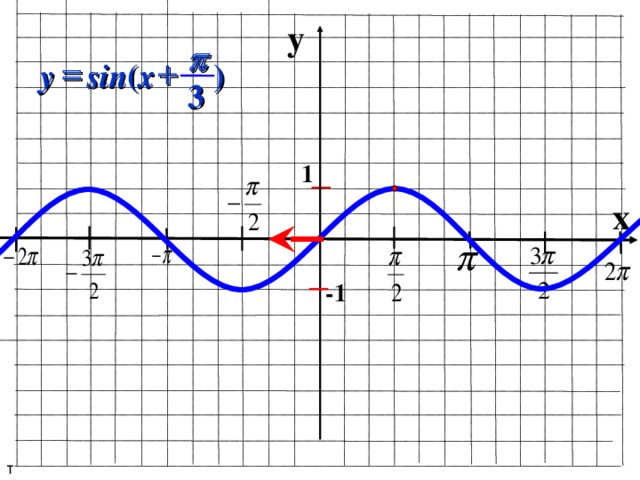
sin (
)
y
x
1
x
-1
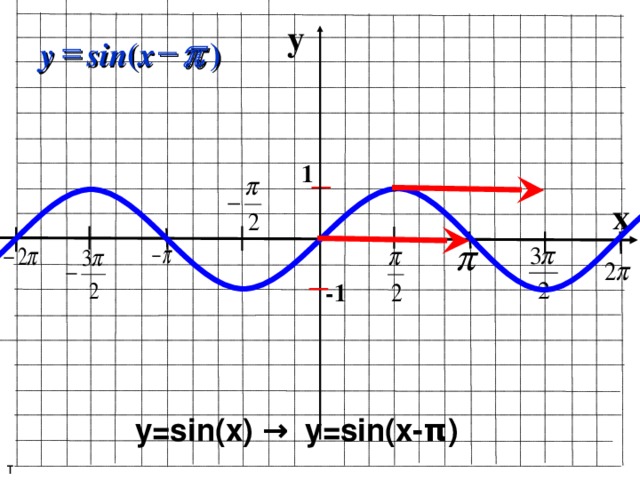
y=sin(x) → y=sin(x- π )
т
y
x
sin (
y
)
2
1
x
-1
у
y
)
y
sin (
x
3
1
x
-1
т
y
1
0
x
- 1
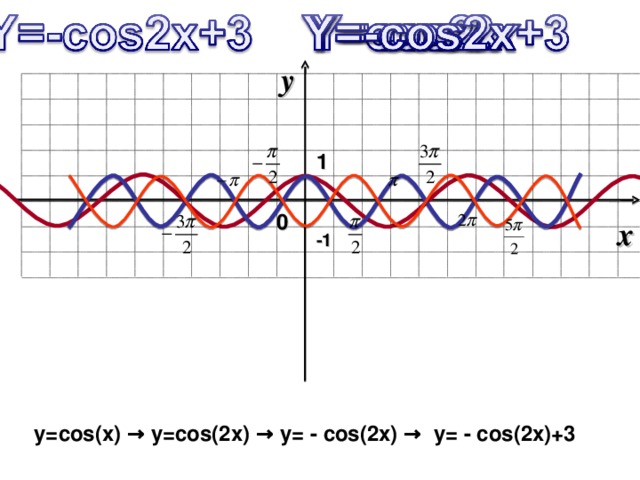
y=cos(x) → y=cos(2x) → y= - cos(2x) → y= - cos(2x)+3
x
x
x
y
y
sin
y
sin
sin
sin
y
-2
x
-2
3
3
3
y
1
0
x
- 1
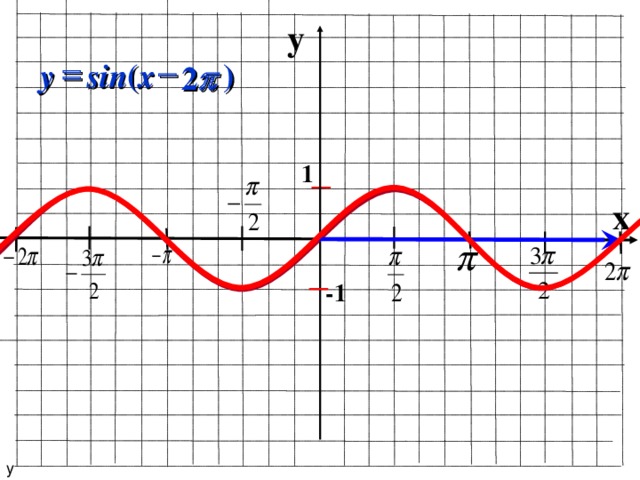
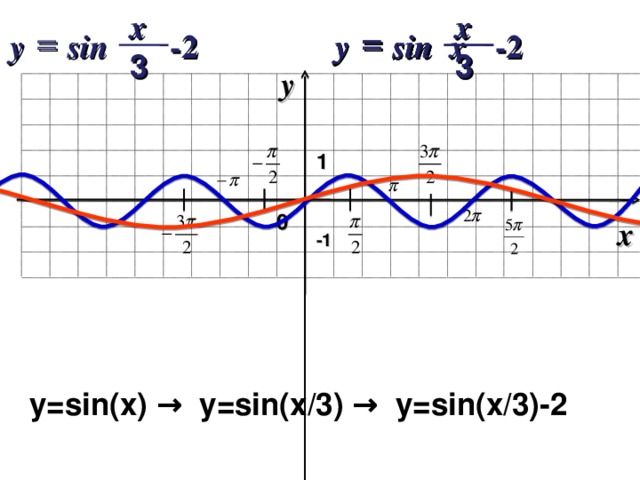
y=sin(x) → y=sin(x/3) → y=sin(x/3)-2
y
1
0
x
- 1
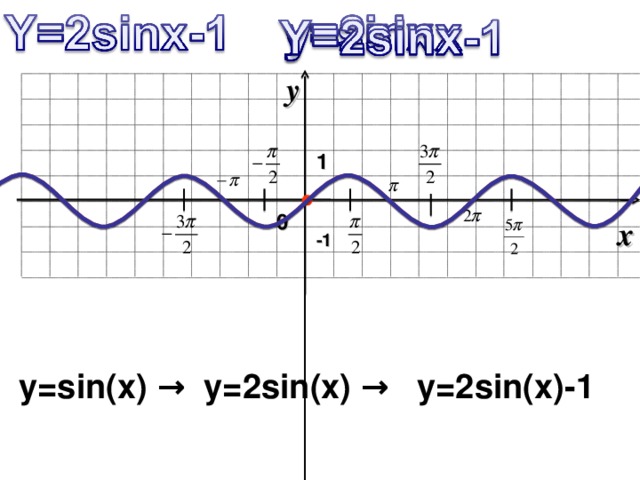
y=sin(x) → y=2sin(x) → y=2sin(x)-1
y
y
y
cos
y
cos x + 2
x
cos x + 2
cos x
2
2
2
y
1
0
x
- 1
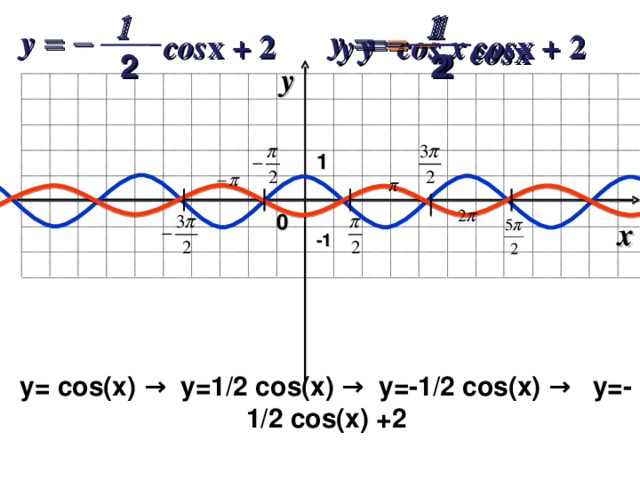
y= cos(x) → y=1/2 cos(x) → y=-1/2 cos(x) → y=-1/2 cos(x) +2
y
1
0
x
- 1
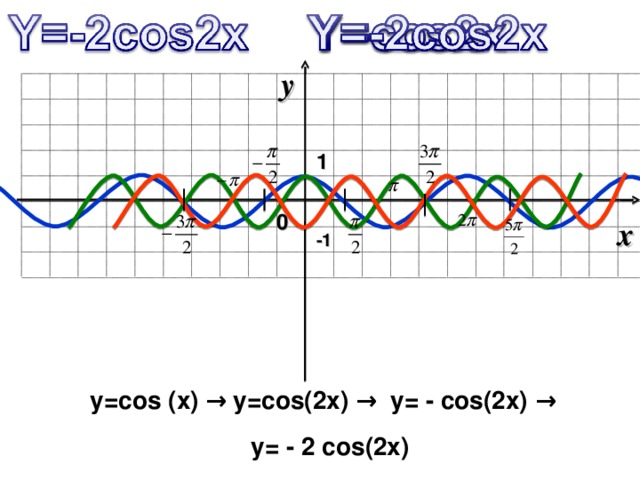
y=cos (x) → y=cos(2x) → y= - cos(2x) →
y= - 2 cos(2x)
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
