Соболева Наталья Владимировна
МЕТОДИКА РАБОТЫ НАД ЗАДАЧАМИ ПО ТЕХНОЛОГИИ УДЕ
Смысл концепции укрупнения дидактических единиц состоит в том, что знания усваиваются системнее, прочнее и быстрее, если они предъявляются ученику сразу крупным блоком во всей системе внутренних и внешних связей. При этом укрупненная дидактическая единица определяется не объемом одновременно выдаваемой информации, а именно наличием связей – взаимно обратными мыслительными операциями, комплексами взаимно-обратных, аналогичных, деформированных и трансформированных задач.
В технологию УДЕ входит методика обучения решению и составлению прямых и обратных задач.
Опыт показывает, что основу интереса к учению составляют глубокие и прочные знания предмета. Нет знаний – нет интереса.
Долгое время задачи находились в хаотическом состоянии, и каждая задача решалась отдельно вне связи с другими.
Ключ к решению задачи – это анализ ее решения, на основе которого устанавливается зависимость между данными и искомыми значениями величин.
В начале ХХ века русский методист Александров провел классификацию арифметических задач по методам решения. Эта классификация дает возможность рассматривать не частные, а общие методы решения задач. Именно этим и должна заниматься школьная математика.
Сравнение этих видов и типов задач показывает, что они постепенно развивают логическое мышление настолько хорошо, что создается возможность практически решать любую арифметическую задачу, встречающуюся в жизни. Поэтому в прежних учебниках однотипные задачи предлагались группами.
В природе не существует стандартных и нестандартных задач. Любая задача сама по себе является нестандартной, но если рядом с ней поместить несколько задач, ей подобных, которые решаются по одному образцу, то такие задачи становятся стандартными, а так как они решаются по одному образцу, то это снижает их обучающее значение.
Каждая задача для своего решения требует определенных размышлений, которые ученик может запомнить и тем самым развивать свою память. А чтобы ученик после прочного уяснения метода решения не мог решать их по шаблону и развивал мышление, надо их усложнять, то есть предлагать с нарастающей трудностью: изменять величину, дополнять условие, использовать прием «недостающих» данных, дополнять и изменять вопрос, решать обратные задачи.
Это достаточно хлопотное дело. Поэтому стали использовать «смешанный» вариант и упрощенный вид. Теперь ученики решают больше задач, чем прежде, но решают бессистемно одни и те же по структуре упрощенные задачи.
Вывод: Главной целью при обучении решению задач является уяснение идеи, общих методов и приемов, что возможно только при надлежащей классификации задач. Никто не оспаривает полезности нестандартных задач, но для их решения ученика еще надо научить соображать и мыслить на типовых задачах с нарастающей трудностью.
Основной традиционный прием анализа задач – разбор от вопроса и от числовых данных. Разбор задачи от вопроса – это суждение, которое состоит в том, чтобы подобрать два числовых значения одной или разных величин таким образом, чтобы дать ответ на вопрос задачи. Одно из значений или оба могут быть неизвестными. Для их нахождения подбираются два других, и так продолжается процесс подбора, пока не приходим к известным числовым значениям величин.
В результате такого разбора учащиеся устанавливают зависимость между числовыми значениями величин, расчленяют ее на простые задачи и составляют план ее решения. Установить связь между числовыми данными задачи и расчленить ее на ряд простых можно и путем разбора от числовых данных.
Разбор задачи от числовых данных состоит в том, что к двум числовым данным подбирается вопрос, затем к следующим двум данным, одно из которых может быть результатом первого действия, подбирается следующий вопрос. И этот процесс продолжается, пока не будет получен ответ на вопрос задачи.
При анализе задачи от вопроса и от числовых данных можно выделить этапы.
На первом этапе необходимо:
научить детей анализировать условие составной задачи и проводить рассуждение при ее разборе от вопроса;
довести до сознания учащихся, что для ответа на вопрос задачи необходимо, чтобы в ее условии было дано не менее двух числовых данных.
Достигнуть этого можно путем решения серий простых задач на все четыре действия без числовых данных, с неполными и полными данными.
На втором этапе решаются задачи в два и три действия с полным анализом и его графической иллюстрацией.
Чтобы сформировать у учащихся понятие анализа составных задач и выработать умение вести рассуждение, необходимо решить значительное количество задач разной структуры. Удобно в ходе решения задач пользоваться схемой. Она дает наглядное представление о разбиении составной задачи на простые и служит опорой мыслительной деятельности учащихся при анализе задачи, как от вопроса, так и от числовых данных.
Ключевым упражнением по УДЕ является составление и решение обратных задач. В методике составления и решения взаимообратных задач наиболее цены не столько сами процессы решения задач как таковые, а переосмысление их содержания с возвратом к первоначальным рассуждениям, то есть составление новых фраз на базе известных слов и чисел.
Все разнообразие простых задач на сложение и вычитание можно представить в виде трех циклов, по три задачи в каждом цикле; всего 9 видов задач. (1-2 класс)
Таблица 1.Классификация простых задач в одно действие на сложение и вычитание
| Цикл | Задачи на сложение | Задачи на вычитание |
-
| Нахождение суммы (прямая задача) | Нахождение 1-ого слагаемого | Нахождение 2-ого слагаемого |
-
| Нахождение уменьшаемого (1-ая обратная задача) | Нахождение остатка (прямая задача) | Нахождение вычитаемого |
-
| Увеличение числа на несколько единиц (прямая задача) | Уменьшение числа на несколько единиц (1-ая обратная задача) | Разностное сравнение (2-ая обратная задача) |
Каждая тройка задач (триада) выступает как некоторая укрупненная дидактическая единица усвоения.
Окончательное усвоение всех разновидностей задач в одно действие осуществляется в теме «Второй десяток».
Все разнообразие простых задач при изучении табличного умножения и деления можно представить в виде трех циклов, по 3 задачи в каждом цикле; всего 9 видов. (2-3 класс)
Таблица 2. Классификация простых задач при изучении табличного умножения и деления
| Цикл | Задачи на умножение | Задачи на деление |
| 1 | Умножение при постоянном множимом (прямая задача) | Деление по содержанию | Деление на равные части |
| 2 | Увеличение числа в несколько раз (прямая задача) | Уменьшение числа в несколько раз | Кратное сравнение |
| 3 | Нахождение числа по величине одной его части | Какую часть составляет одно число от другого | Нахождение одной части числа (прямая задача) |
В 3-4 классах решаются составные задачи в несколько действий, получаемые комбинацией указанных выше видов задач.
При системе укрупнения одновременное решение какой-либо задачи мозг в подсознательной сфере обрабатывает и две другие задачи-следствия, обратные первой. Развивается ассоциативное мышление. Посредством сочинения взаимно-обратных задач общий способ действия сохраняется в кратковременной памяти. Следовательно, более прочным оказывается долговременный след. Обратная задача для школьника – это своего рода исследовательская задача.
Так происходит обобщение приемом рассуждения, слияние взаимосвязанных видов задач в группу родственных задач как крупную единицу усвоения. Это и приводит, в конечном счете, к ускоренному усвоению математики.
А сейчас я хочу предложить вам методику работы над задачами в несколько действий.
Рассмотрим задачу: "У воспитательницы в коробке лежало 40 пуговиц. Она пришила к 7 рубашкам по 4 пуговицы. Сколько пуговиц осталось в коробке?"
После прочтения задачи находим условие и требование, а затем записываем линейную краткую запись:
Было Пришила Осталось
 40 п.,/ к 7 руб. по 4 пуг.,/ пуг.
40 п.,/ к 7 руб. по 4 пуг.,/ пуг.
(Слова над каждой частью задачи можно записывать сокращенно буквами)
Что показывает в этой задаче число 40? 7? 4?
В какой части находится неизвестное число? (В 3-ей)
Что нужно узнать?
Расскажите эту задачу, опираясь на линейную краткую запись.
Если неизвестное число находится в третьей части, то с какой части начнем решать задачу? (Со второй)
Почему со второй, я не с первой? (Потому что там два числа, а должно быть одно)
Что нужно узнать сначала? (Сколько пуговиц пришили к семи рубашкам.)
Как будем узнавать? (4 х 7 = 28 (п.))
Найденное число записываем над второй частью.
Если мы знаем, сколько пуговиц было в коробке сначала и сколько их пришили к 7 рубашкам, как узнать, сколько пуговиц осталось? (40 - 28 = 12 (п.))
Давайте составим выражение к этой задаче. Что мы узнавали сначала? Как мы это делали? Что узнавали потом? Как мы это делали? (40-4х7 = 22(п.))
Аналогичным образом, отвечая на эти же вопросы, чертим граф - схему:
4
7

 х
х
4000
28
=
 -
-
12
=
С опорой на эту же линейную краткую запись переходим к составлению и решению обратных задач.
Вместе с детьми решаем, какое число у нас будет неизвестным, обводим его в "окошко" цветным карандашом.
Составляем обратную задачу так, чтобы неизвестным было выбранное число, например, число 4 пуговицы: "У воспитательницы в коробке лежало 40 пуговиц. Она пришила к 7 рубашкам по несколько пуговиц, после чего у нее в коробке осталось 12 пуговиц. По сколько пуговиц она пришила к каждой рубашке?"
 Было Пришила 28 п. Осталось
Было Пришила 28 п. Осталось
40 п.,/ к 7 руб. по пуг.,/ 12 пуг.
Переписывать краткую запись не нужно. Достаточно внести в имеющуюся запись уточнения: вписать в «окошко» число 12 и цветным карандашом обвести число 4.
Что показывает в этой задаче число 40? 7? 12?
В какой части находится неизвестное число? (Во 2-ой)
С какой(их) части(ей) начнем решать задачу? (С 1-ой и с 3-ей)
Что нужно узнать сначала? (Сколько пуговиц всего пришила.)
Как это можно узнать? (40-12=28 (п.))
Если воспитательница пришила к 7 рубашкам 28 пуговиц, как узнать, сколько пуговиц она пришила к 1 рубашке? (28:7=4 (п.))
Давайте составим выражение к этой задаче. Что мы узнавали сначала? Как мы это делали? Что узнавали потом? Как мы это делали? ((40-12):7=4(п.))
Аналогичным образом, отвечая на эти же вопросы, вносим дополнения в имеющуюся граф – схему цветным карандашом.
7
4
 =
=

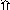 х
х
4000
28
= :
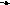
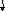
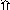 -
-
12
 - =
- =
Таким же образом составляются и 2 другие обратные задачи.
Итак, на одном уроке дети составили и решили 1 прямую и 3 обратных задачи. Линейная краткая запись служила опорой для слабых учеников.
Взаимосвязанные задачи сливаются в группу родственных задач как крупную единицу усвоения (триада задач). Девять видов задач преобразуется в три вида, что приводит к ускоренному циклу усвоения математики и обобщению приемов рассуждений.
Таким образом, в методологии укрупненных дидактических единиц делается акцент на стратегию понимания, а не на частные упражнения.
Для учащихся, которые затрудняются составить план решения, ведется более подробный анализ.
ПОЛНЫЙ АНАЛИЗ СОСТАВНОЙ ЗАДАЧИ.
Памятка по решению задач.
1. Прочитай задачу.
2. Изобрази на схеме ее условие.
3. Объясни, что показывает каждое число. Сформулируй главный вопрос задачи.
4. Представь себе мысленно, о чем говорится в задаче, расскажи вслух.
5. Подумай, что можно сказать о числе, которое получится в ответе. Сравни его с данными задачи и скажи, больше или меньше получится число.
6. Сделай анализ задачи, то есть подумай над вопросом: можно ли сразу ответить на главный вопрос задачи? Если нельзя, то почему? Что надо знать для ответа на главный вопрос задачи?
7. Затем, после анализа, подумай и расскажи план решения.
8. Выполни его.
9. Подумай, нельзя ли решить задачу другим способом.
10. Проверь ответ и запиши.
Основными в памятке являются советы обдумать, что надо знать для ответа на вопрос задачи (указать, какие два данных необходимы для ответа на вопрос задачи) и что можно узнать из данных и условия задачи.
Теперь более конкретно рассмотрим на примере составной задачи:
На дачном участке посадили 5 грядок с помидо-рами по 9 кустов на каждой грядке и 3 грядки с огурцами по 8 кустов на каждой грядке. Сколько всего кустов с овощами посадили на дачном участке?
1.Чтение задачи (про себя, вслух).
2.Выделить только условие, только вопрос.
3.Какие величины встретились в задаче?
( количество грядок; посадила на 1-й грядке; посадила на всех грядках)
РАЗБОР ЧИСЛОВЫХ ЗНАЧЕНИЙ И ЗАПИСЬ В ТАБЛИЦУ:
Что обозначает число 5?
( количество грядок с помидорами )
Что обозначает число 9?
( сколько кустов с помидорами на 1-й грядке )
Что обозначает число 3?
(количество грядок с огурцами )
Что обозначает число 8?
( сколько кустов с огурцами на 1-й грядке )
Что нужно узнать?
( сколько всего кустов с овощами посадили на этих грядках )
Как это обозначить? (фигурной скобкой и ? знаком)
На доске появляется запись:
| | Посадили на 1-й грядке. | Количество грядок. | Посадили на все грядки. |
| Помидоров | 9 к. |
5 гр. |  ? к. ? к.
? |
| Огурцов | 8 к. | 3 гр. | ? к. |
Или:
Помидоров - ? к, 5 гр. по 9 к.
?
Огурцов - ? к, 3 гр. по 8 к.
-Какая это задача? (составная)
-Почему? (найти сколько всего кустов посадили с помидорами и огурцами мы не можем)
-Что нужно знать, чтобы ответить на вопрос задачи?
(сколько на всех грядках кустов с помидо и сколько на всех грядках кустов с огурцами )
-Что из этого известно? (ничего) –отмечаем эти вопросы в таблице
-Сколько вопросов в задаче? (3).
-Можем ли мы узнать сколько кустов помидоров на 5 грядках?
(да, для этого нужно знать сколько кустов помидоров посадилина 1-й грядке и количество этих грядок)
-Можем ли мы узнать сколько кустов огурцов на 3 грядках?
(да, для этого нужно знать сколько кустов огурцов посадили на 1-й грядке и количество этих грядок)
-Можем ли теперь ответить на главный вопрос задачи?
(да, для этого ко всем кустам помидоров прибавить все посаженные кусты огурцов и в результате получим сколько кустов овощей посадили )
ПЛАН РЕШЕНИЯ ЗАДАЧИ:
-Что узнаете 1 действием?
(сколько всего кустов помидоров посадили)
-Как узнаете?
(выбираем действие умножения)
-Что узнаете 2 действием?
(сколько всего кустов огурцов посадили)
-Как узнаете?
(выбираем действие умножения)
-Что находим 3 действием?
(сколько всего кустов овощей посадили на участке)
-Как?
(чтобы узнать, сколько всего кустов овощей посадили выбираем
действие сложения)
СОСТАВЛЯЕМ ВЫРАЖЕНИЕ ПО ЗАДАЧЕ:
В задаче спрашивается, сколько кустов с овощами посадили
на участке – поэтому выбираем действие сложения.
Первое слагаемое выражено произведением чисел 9 и 5,
второе слагаемое выражено произведением чисел 8 и 3.
посадили на все + посадили на все = посадили на все
грядки помидоры грядки огурцы грядки овощей
9х5 + 8х3 = 69 (к.)
Алгоритм рассуждения
при работе над задачей
По условию задачи дано …
Спрашивается …
Для ответа на вопрос надо знать …
Нам известно …
Неизвестно …, но сказано, что …
Значит сначала узнаем, сколько …
А потом узнаем …
Решаю.
Пишу ответ.
Образец рассуждения.
Задача.
У Пети было 15 рублей, а у Вити на 10 рублей больше. Сколько денег было у мальчиков?
Ученик, пользуясь карточкой – помощницей начинает рассуждать:
По условию задачи дано , что у Пети было 15 рублей, а у Вити на 10 рублей больше.
Спрашивается : сколько денег было у мальчиков?
Для ответа на вопрос надо знать, сколько денег было у Пети, и сколько денег было у Вити.
Нам известно, что у Пети было 15 рублей.
Неизвестно, сколько денег было у Вити, но сказано, что у Вити было на 10 рублей больше.
Значит сначала узнаем, сколько денег было у Вити.
А потом узнаем, сколько денег было у мальчиков.
Решаю:
1) 15 + 10 = 25 (р.) у Вити.
2) 15 + 25 = 40 (р.)
или: 15 + (15 + 10) = 40
9.Ответ : 40 рублей было у мальчиков.


 х
х 
 -
-  =
=  х
х  - =
- = 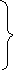 ? к.
? к.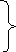

 ? к.
? к. 





























