( алгоритм)
I курс
алгебра
Алгоритм
Найти область определения функции Определить чётность функции Найти точки пересечения графика с осями координат Найти f ´(x) – производную функции Найти критические точки функции Установить промежутки монотонности и экстремумы Найти значения функции в критических точках Полученные сведения о производной функции и о функции поместить в таблицу Построить график функции 1 2 3 4 5 67
Примеры
Область определения функции
функция задаётся формулой область определения – это множество значений аргумента “x” функции, при которых выполняются действия, указанные в формуле область определения обозначается “D” при нахождении области определения надо обращать внимание на действия: деление, извлечение квадратного корня ; У = х 2 +1
у
у
у
У = √ х
х
0
0
х
х
0
У = - 6 /х
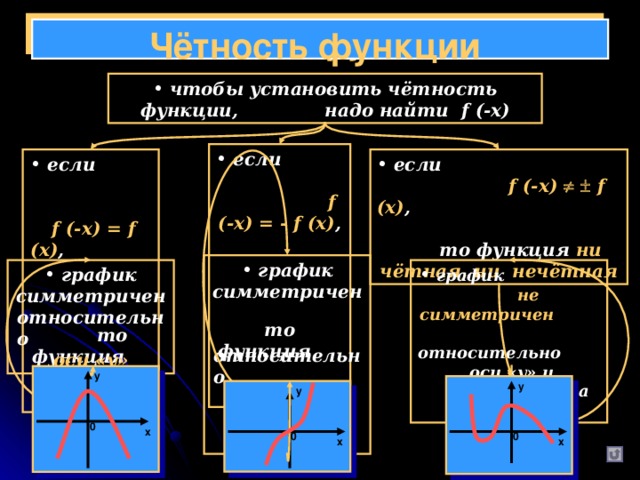
Чётность функции
чтобы установить чётность функции, надо найти f (-x) если f (-x) = - f (x) , то функция нечётная если f (-x) f (x) , то функция ни чётная, ни нечётная если f (-x) = f (x) , то функция чётная график симметричен относительно начала координат график не симметричен относительно оси «у» и начала координат график симметричен относительно оси «у» у
у
у
0
х
0
0
х
х
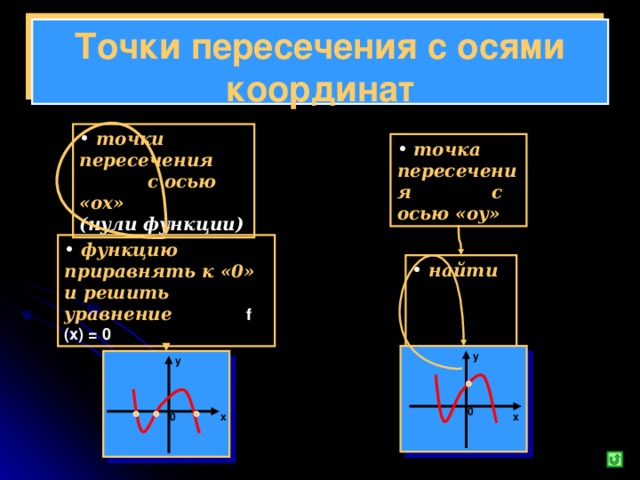
Точки пересечения с осями координат
точки пересечения с осью «ох» (нули функции) точка пересечения с осью «оу» функцию приравнять к «0» и решить уравнение f (x) = 0 у
у
0
х
х
0
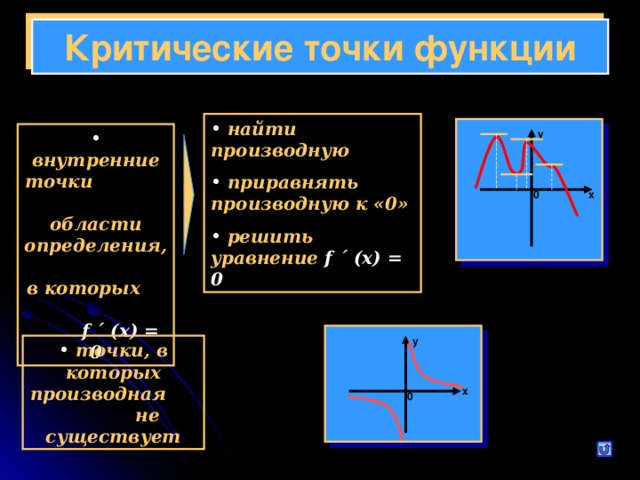
Критические точки функции
найти производную приравнять производную к «0» решить уравнение f ´ (x) = 0 внутренние точки области определения, в которых f ´ (x) = 0 у
х
0
у
точки, в которых производная не существует х
0
Промежутки монотонности и экстремумы
f ´(x) 0 f (x)
f ´(x) f (x)
f (x)
f ´(x)
х 1
х 6
х 5
х 4
х 2
х 3
+
+
-
-
+
-
+
max
max
min
min
перегиб
перегиб
Таблица
x
(-∞; x 1 )
f ´(x)
+
f (x)
x 1
(x 1 ; x 2 )
0
-
x 2
f (x 1 )
m a x
0
(x 2 ; x 3 )
+
x 3
f (x 2 )
0
(x 3 ; +∞)
m i n
+
f (x 3 )
П е р е г и б
График
На координатной плоскости отметить:
Точки пересечения с осью «х» Точку пересечения с осью «у» Точки минимума, максимума, перегиба При проведении кривой через точки учитывать
Область определения функции Симметричность графика функции Промежутки возрастания и убывания функции
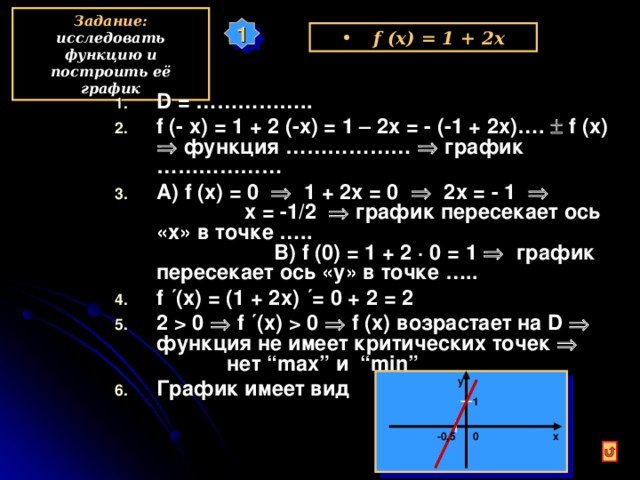
Задание: исследовать функцию и построить её график
1
D = …………….. f (- x) = 1 + 2 (-x) = 1 – 2x = - (-1 + 2x)…. f (x) функция ……………… график ……………… А) f (x) = 0 1 + 2x = 0 2x = - 1 x = -1/2 график пересекает ось «х» в точке ….. В) f ( 0 ) = 1 + 2 · 0 = 1 график пересекает ось «у» в точке ….. f ´ (x) = (1 + 2x) ´= 0 + 2 = 2 2 0 f ´ (x) 0 f (x) возрастает на D функция не имеет критических точек нет “max” и “min” График имеет вид у
1
х
0
-0,5
Задание: исследовать функцию и построить её график
2
D = …………….. f (- x) = 2 - 3 (-x) = 2 + 3 x = - (- 2 - 3 x)…. f (x) функция ……………… график ……………… А) f (x) = 0 2 - 3 x = 0 - 3 x = - 2 x = 2 / 3 график пересекает ось «х» в точке ….. В) f ( 0 ) = 2 - 3 · 0 = 2 график пересекает ось «у» в точке ….. f ´ (x) = (2 - 3 x) ´= 0 - 3 = - 3 - 3 f ´ (x) f (x) убывает на D функция не имеет критических точек нет “max” и “min” График имеет вид у
2
х
0
2/3
Задание: исследовать функцию и построить её график
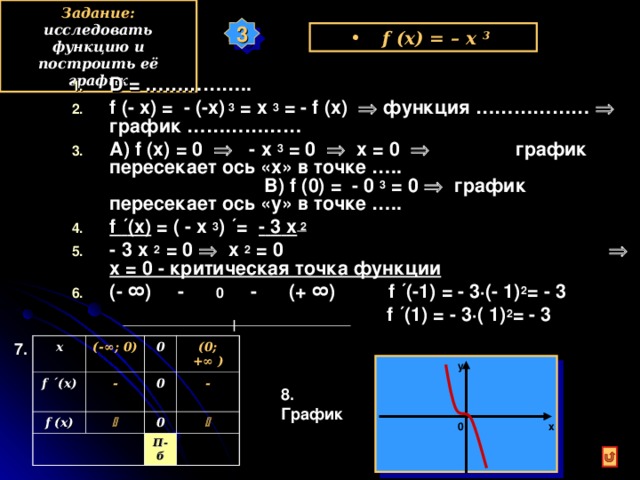
3
D = …………….. f (- x) = - (-x) 3 = x 3 = - f (x) функция ……………… график ……………… А) f (x) = 0 - x 3 = 0 x = 0 график пересекает ось «х» в точке ….. В) f ( 0 ) = - 0 3 = 0 график пересекает ось «у» в точке ….. f ´ (x) = ( - x 3 ) ´= - 3 х 2 - 3 х 2 = 0 х 2 = 0 х = 0 - критическая точка функции ( - ∞ ) - 0 - ( + ∞ ) f ´(-1) = - 3·(- 1) 2 = - 3 f ´(1) = - 3·( 1) 2 = - 3
7.
x
(-∞; 0)
f ´(x)
0
f (x)
-
(0; +∞ )
0
-
0
П - б
у
8. График
0
х
4
Задание: исследовать функцию и построить её график
Вариант II
Вариант I
Вариант III
f(x)
1
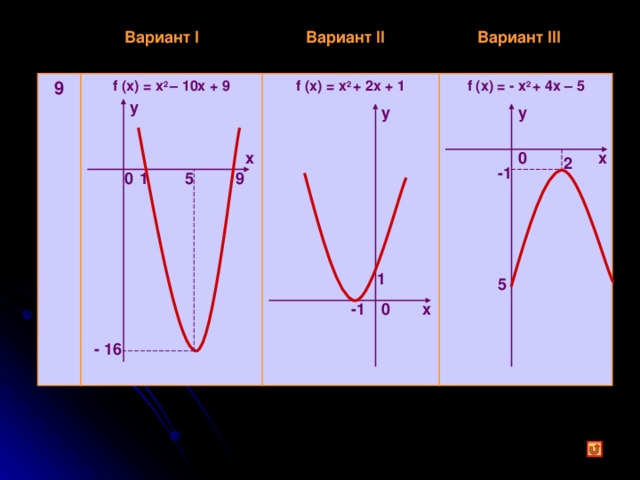
f(x) = x 2 – 10x + 9
D = (- ∞; +∞)
f(x) = x 2 + 2x + 1
2
f(x) = - x 2 + 4x - 5
D = (- ∞; +∞ )
f( - x)= (- x ) 2 – 10 (- x ) + 9 = = х 2 + 10х + 9 f(x) функция ни чётная, ни нечётная
3
D = (- ∞; +∞)
f( - x) = (- x ) 2 + 2 (- x ) + 1 = = х 2 – 2х + 1 f(x) функция ни чётная, ни нечётная
А) «нули» функции:
x 2 – 10x + 9 = 0
D = 64
x 1 = 1 x 2 = 9 график пересекает ось «х» в точках: (1; 0) , (9;0)
В) f (0) = 9 график пересекает ось «у» в точке (0;9)
f( - x) = - (- x ) 2 + 4 (- x ) –5 =
= - х 2 - 4х - 5 f(x) функция ни чётная, ни нечётная
А) «нули» функции:
x 2 + 2 x + 1 = 0
D = 0
х = - 1 график пересекает ось «х» в точке (-1; 0)
В) f (0) = 1 график пересекает ось «у» в точке (0;1)
А) «нули» функции:
- x 2 + 4 x - 5 = 0
D = - 4 уравнение корней не имеет график не пересекает ось «х»
В) f (0) = - 5 график пересекает ось «у» в точке (0;-5)
Вариант I
Вариант III
Вариант II
4
f ´ (x) = (x 2 – 10x + 9) ´ = = 2x - 10
5
f ´ (x) = (x 2 + 2x + 1) ´=
= 2x + 2
f ´ (x) = 0
2x – 10 = 0
2x = 10 x = 5 - критическая точка
6
f ´ (x) = (- x 2 + 4x – 5) ´=
= - 2x + 4
f ´ (x) = 0
2x + 2 = 0
2х = - 2 х = - 1 – критическая точка
f ´ ( 1 ) = 2 · 1 – 10 = - 8
f ´ ( 6 ) = 2 · 6 – 10 = 2
7
f ´ (x) = 0
- 2x + 4 = 0
- 2х = - 4
х = 2 – критическая точка
8
f( 5 )= 5 2 – 10 · 5 + 9 = - 16
f ´ ( -2 ) = 2 · (-2) + 2 = - 2
f ´ ( 0 ) = 2 · 0 + 2 = 2
f( -1 )= (-1) 2 + 2 · (-1) + 1 = 0
f ´ ( 0 ) = - 2 · 0 + 4 = 4
f ´ ( 3 ) = - 2 · 3 + 4 = - 2
f ( 2 ) = - 2 2 + 4 · 2 – 5 = -1
+
-
+
+
-
-
- 1
2
5
х
х
х
f ´(x)
(- ∞;2)
f ´(x)
(- ∞;-1)
(- ∞;5)
f ´(x)
f (x)
-1
5
f (x)
2
f (x)
-
+
-
(-1;+ ∞)
(2;+ ∞)
(5;+ ∞)
0
0
0
-
-1
0
+
+
-16
min
min
max
Вариант I
Вариант II
Вариант III
9
f (x) = x 2 – 10x + 9
f (x) = x 2 + 2x + 1
f (x) = - x 2 + 4x – 5
y
y
y
0
x
x
2
-1
5
1
0
9
1
5
0
-1
x
- 16
Задание: исследовать функцию и построить её график
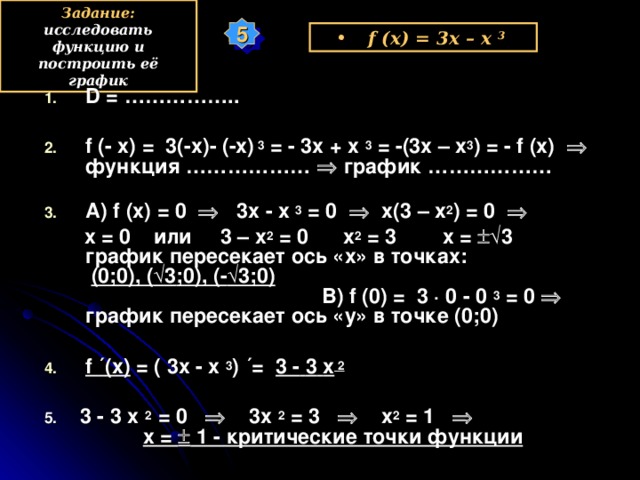
5
D = …………….. f (- x) = 3(-x) - (-x) 3 = - 3x + x 3 = -(3x – x 3 ) = - f (x) функция ……………… график ……………… А) f (x) = 0 3x - x 3 = 0 x(3 – x 2 ) = 0 x = 0 или 3 – x 2 = 0 x 2 = 3 x = √3 график пересекает ось «х» в точках: (0;0), ( √3 ;0), (- √3 ;0) В) f ( 0 ) = 3 · 0 - 0 3 = 0 график пересекает ось «у» в точке (0;0)
f ´ (x) = ( 3х - x 3 ) ´= 3 - 3 х 2
5. 3 - 3 х 2 = 0 3х 2 = 3 х 2 = 1 х = 1 - критические точки функции
у
х
-
-
+
6.
f ´ (- 2 ) = 3 - 3 (- 2 ) 2 = 3 - 12 = - 9
f ´ ( 0 ) = 3 - 3 ( 0 ) 2 = 3 0 f ´ ( 2 ) = 3 - 3 ( 2 ) 2 = 3 - 12 = - 9
f (- 1) = 3(-1) - (-1) 3 = - 3 + 1 3 = - 2 f ( 1 ) = 3 · 1 - 1 3 = 3 - 1 = 2
8.
- 1
1
x
f ´(x)
(- ∞; -1)
f (x)
-
-1
( -1; 1)
0
+
1
- 2
0
(1;+ ∞)
min
2
-
max
y
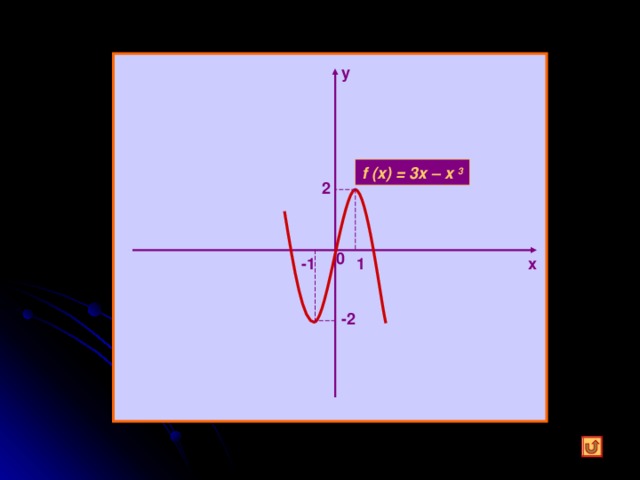
f (x) = 3x – x 3
2
0
1
-1
x
-2
Задание: исследовать функцию и построить её график
6
D = …………….. f (- x) = (-x) 4 - 50 (-x) 2 = x 4 - 50 x 2 = f (x) функция ……………… график ……………… А) f (x) = 0 x 4 - 50 x 2 = 0 x 2 (x 2 – 50) = 0 x = 0 или x 2 - 50 = 0 x 2 = 50 x = 5 √ 2 (≈ 7,1) график пересекает ось «х» в точках: (0;0), (- 7,1 ;0), (7,1;0) В) f ( 0 ) = 0 4 – 50 · 0 2 = 0 график пересекает ось «у» в точке (0;0)
f ´ (x) = (x 4 - 50 x 2 ) ´= 4 х 3 – 50 · 2х = 4х 3 – 100х
4х 3 – 100х = 0 | : 4 х 3 – 25 х = 0 х(х 2 – 25) = 0 х = 0 или х 2 – 25 = 0 х 2 = 25 х = 5 х = 5 - критические точки функции х = 0
у
}
х
+
-
+
-
6.
f ´ (- 6) = (- 6) 3 - 25(- 6) = - 216 + 1 50
f ´ (- 1) = (- 1) 3 - 25(- 1) = -1 + 25 0 f ´ ( 1) = 1 3 – 25 · 1 2 = 1 - 2 5
f ´ ( 6) = 6 3 – 25 · 6 = 216 - 1 50 0
f ( ± 5) = ( ± 5) 4 - 50 · ( ± 5) 2 = 625 - 1250 = - 625 f (0) = 0
8.
- 5
5
0
x
f ´(x)
(- ∞; - 5)
f (x)
- 5
-
( - 5; 0)
0
0
- 625
+
m I n
0
( 0; 5)
5
0
-
m a x
(5;+ ∞)
0
+
- 625
m I n
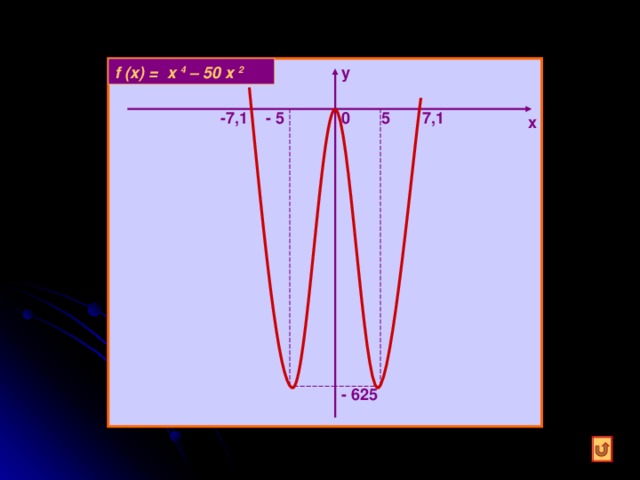
f (x) = x 4 – 50 х 2
y
5
- 5
-7,1
7,1
0
x
- 625
Задание: исследовать функцию и построить её график
7
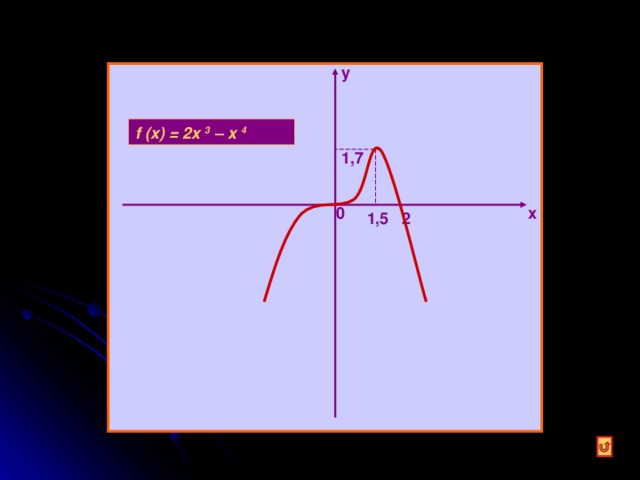
D = …………….. f (- x) = 2(-x) 3 - (-x) 4 = - 2x 3 - x 4 = -(2x 3 + x 4 ) ± f (x) функция ……………… график ……………… А) f (x) = 0 2x 3 - x 4 = 0 x 3 (2 – x) = 0 x = 0 или 2 – x = 0 x = 2 график пересекает ось «х» в точках: (0;0), ( 2 ;0 ) В) f ( 0 ) = 3 · 0 - 0 3 = 0 график пересекает ось «у» в точке (0;0)
f ´ (x) = ( 2 х 3 - x 4 ) ´= 2 · 3 x 2 - 4 х 3 = 6x 2 - 4 х 3
6x 2 - 4 х 3 = 0|:2 3х 2 – 2x 3 = 0 х 2 (3 – 2x) = 0 x = 0 или 3 – 2х = 0 х = 1,5 х = 0 - критические точки функции х = 1,5
у
}
х
-
+
+
6.
f ´ (- 1) = 3(- 1) 2 - 2(- 1) 3 = 3 + 2 = 5 0 f ´ ( 1) = 3 · 1 2 - 2 · 1 3 = 3 - 2 = 1 0
f ´ ( 2) = 3 · 2 2 - 2 · 2 3 = 12 - 16 = – 4
f (1,5) = 2 · (1,5) 3 – (1,5) 4 = 2 · 3,375 – 5,0625 ≈ 1,7 f (0) = 0
8.
1,5
0
x
f ´(x)
(- ∞; 0)
f (x)
+
0
0
( 0; 1,5)
+
1,5
0
0
(1,5;+ ∞)
Пе ре гиб
1,7
-
m a x
y
f (x) = 2x 3 – x 4
1, 7
0
x
2
1,5
0 f (x) f ´(x) f (x) f (x) f ´(x) х 1 х 6 х 5 х 4 х 2 х 3 + + - - + - + max max min min перегиб перегиб" width="640"
0 f ´ (x) 0 f (x) возрастает на D функция не имеет критических точек нет “max” и “min” График имеет вид у 1 х 0 -0,5" width="640"
0 f ´ ( 2 ) = 3 - 3 ( 2 ) 2 = 3 - 12 = - 9 f (- 1) = 3(-1) - (-1) 3 = - 3 + 1 3 = - 2 f ( 1 ) = 3 · 1 - 1 3 = 3 - 1 = 2 8. - 1 1 x f ´(x) (- ∞; -1) f (x) - -1 ( -1; 1) 0 + 1 - 2 0 (1;+ ∞) min 2 - max" width="640"
0 f ´ ( 1) = 1 3 – 25 · 1 2 = 1 - 2 5 f ´ ( 6) = 6 3 – 25 · 6 = 216 - 1 50 0 f ( ± 5) = ( ± 5) 4 - 50 · ( ± 5) 2 = 625 - 1250 = - 625 f (0) = 0 8. - 5 5 0 x f ´(x) (- ∞; - 5) f (x) - 5 - ( - 5; 0) 0 0 - 625 + m I n 0 ( 0; 5) 5 0 - m a x (5;+ ∞) 0 + - 625 m I n" width="640"
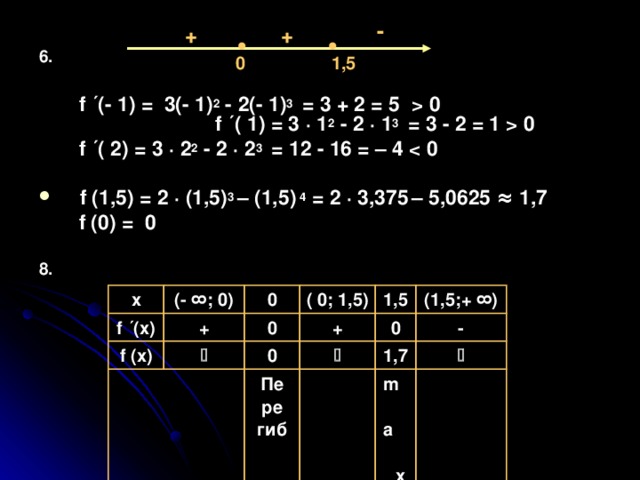0 f ´ ( 1) = 3 · 1 2 - 2 · 1 3 = 3 - 2 = 1 0 f ´ ( 2) = 3 · 2 2 - 2 · 2 3 = 12 - 16 = – 4 f (1,5) = 2 · (1,5) 3 – (1,5) 4 = 2 · 3,375 – 5,0625 ≈ 1,7 f (0) = 0 8. 1,5 0 x f ´(x) (- ∞; 0) f (x) + 0 0 ( 0; 1,5) + 1,5 0 0 (1,5;+ ∞) Пе ре гиб 1,7 - m a x" width="640"
