| Вспомним основные понятия, связанные с уравнением. Прежде всего, что такое уравнение?
Какие еще понятия связаны с уравнением?
Что называется ОДЗ уравнения? Найдите ОДЗ следующих уравнений. 1) 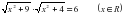 , , 2) 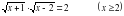 , , 3) 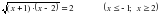 , , 4) 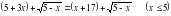 , , 5) 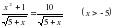 6)  . .
|
Уравнение – это аналитическая запись задачи нахождения значений аргументов, при которых значения одной функции равны значениям другой функции .
Корень уравнения – это число, при подстановке которого в уравнение получается верное числовое равенство. Решить уравнение – найти все его корни или установить, что их нет.
Множество всех чисел, при которых имеют одновременно смысл функции, стоящие в левой и правой частях уравнения.
|
| На доске записано решение уравнения 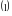
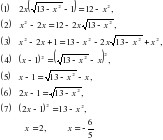
Что представляет собой процесс решения уравнения? - Верно, т.е. происходит последовательность упрощений от уравнения 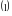 к уравнению к уравнению 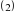 и т.д. к и т.д. к 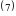 . Проследим, что происходит с корнями уравнения на каждом этапе преобразований. В представленном решении получены два корня уравнения . Проследим, что происходит с корнями уравнения на каждом этапе преобразований. В представленном решении получены два корня уравнения 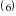 . Проверьте, являются ли числа . Проверьте, являются ли числа 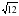 и и 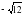 корнями исходного уравнения корнями исходного уравнения 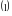 . . - Значит, в процессе решения эти корни были потеряны. В целом же выполненные преобразования привели к потере двух корней 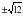 и приобретению постороннего корня и приобретению постороннего корня 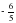 . .
- Как можно избавиться от посторонних корней?
- Допустима ли потеря корней? Почему?
- Как же избежать потери корней?
- Итак, чтобы процесс решения уравнения приводил к верным результатам, что важно знать при выполнении преобразований над уравнениями?
- Вот этим мы и займемся на этом уроке. Как бы вы сформулировали цель предстоящей деятельности на сегодняшнем уроке?
|
Выполнение преобразований, приводящих данное уравнение к уравнению более простого вида, т.е. такого уравнения, нахождение корней которого не представляется трудным.
Числа  , , 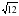 и и 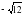 являются корнями исходного уравнения, а являются корнями исходного уравнения, а 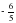 - нет - нет
Сделать проверку.
Нет, т.к. решить уравнение – это найти все его корни.
Наверное, при решении уравнения не выполнять преобразования, которые ведут к потере корней.
Наверное, знать, какие преобразования над уравнениями сохраняют корни, какие приводят к потере корней или приобретению посторонних корней. Знать, какими преобразованиями их можно заменить, чтобы потери или приобретения корней не было.
Выявить преобразования над уравнениями, которые сохраняют корни, приводят к потере корней или приобретению посторонних корней. Знать, какими преобразованиями их можно заменить, чтобы потери или приобретения корней не было |
| Откроем тетради, запишем сегодняшнюю дату 11декабря и тему урока «равносильные уравнения» Обратимся снова к уравнению, записанному на доске. Проследим, на каком этапе и в результате каких преобразований, были потеряны два корня и появился посторонний. (Учитель справа от каждого уравнения 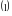 - -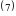 проставляет числа). проставляет числа).
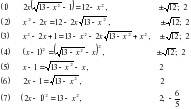
- Назовите уравнения, имеющие один и тоже набор (множество) корней. - Такие уравнения называются равносильными. Попытайтесь сформулировать определение равносильных уравнений. - Запишем определение. Определение 1. Уравнения 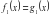 и и 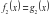 называются равносильными, если множества их корней совпадают. называются равносильными, если множества их корней совпадают. Необходимо отметить, что уравнения не имеющие коней, также являются равносильными. Для обозначения равносильных уравнений можно использовать символ «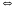 ». Процесс решения уравнения ». Процесс решения уравнения 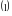 , используя новое понятие, можно отразить так: , используя новое понятие, можно отразить так: 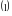 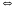 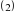 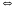 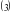 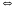 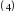 … …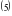 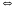 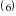 … …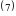 . .
Таким образом, переход от данного уравнения к равносильному не влияет на множество корней получающегося уравнения. А какие основные преобразования выполняли при решении линейных уравнений?
Менялись ли при этом их корни?
Перенос слагаемых из одной части уравнения в другую, меняя при этом знак на противоположный, в 7-м классе сформулировали свойство уравнений. Сформулируйте его, применив новое понятие.
Какое еще свойство уравнения вы знаете?
Применение этого свойства также заменяет исходное уравнение на равносильное ему. Обратимся опять к уравнению, записанному на доске. Сравните множество корней уравнений 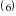 и и 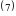 ? ?
То есть при переходе одного уравнения к другому множество корней хотя и расширилось, но потери корней не произошло. В этом случае уравнение 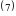 называют следствием уравнения называют следствием уравнения 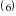 . Попытайтесь сформулировать определение уравнения, которое является следствием данного уравнения. . Попытайтесь сформулировать определение уравнения, которое является следствием данного уравнения.
Определение 2. Уравнение 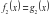 называют следствием уравнения называют следствием уравнения 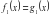 , если каждый корень уравнения , если каждый корень уравнения 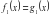 является корнем уравнения является корнем уравнения 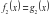 . .
В результате какого преобразования получили уравнение 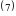 из уравнения из уравнения 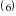 ? ?
Значит, это преобразование может приводить к появлению посторонних корней, т.е. исходное уравнение преобразуется в уравнение-следствие. Есть ли еще уравнения-следствия в представленной цепочке преобразований уравнения 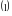 ? ?
А какие это уравнения?
-Попытайтесь, используя понятие уравнения-следствия, сформулировать эквивалентное определение равносильных уравнений.
- Есть ли еще уравнения-следствия в предложенном решении уравнения 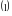 ? ? - Что происходит с корнями при переходе от 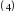 к к 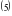 ? ?
- В результате какого преобразования это произошло?
|
Уравнения 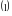 , , 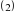 , ,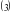 , ,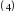 и и 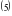 , ,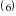
Уравнения, имеющие одно и тоже множество корней, называются равносильными.
Раскрытие скобок; перенос слагаемых из одной части уравнения в другую, изменяя знак на противоположный; прибавление к обеим частям уравнения выражения, содержащее неизвестную.
Нет.
Если какой-нибудь член уравнения перенести из одной части уравнения в другую с противоположным знаком, то получится уравнение, равносильное данному.
Обе части уравнения можно умножать на одно и тоже число, отличное от нуля.
Корень уравнения 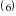 является корнем уравнения является корнем уравнения 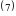 . .
Если при переходе от одного уравнения к другому потери корней не происходит, то второе уравнение называют следствием первого уравнения.
Возведение в квадрат обеих частей уравнения.
Да, например, уравнение 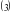 - следствие уравнения - следствие уравнения 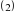 , а уравнение , а уравнение 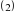 - следствие уравнения (3). - следствие уравнения (3).
Равносильные.
Уравнения называются равносильными, если каждое из них является следствием другого.
Да, уравнение 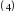 - следствие уравнения - следствие уравнения 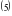 . .
Потеряны два корня.
Ошибка в применении тождества  |
| - Обратимся к уравнениям группы а), являются ли эти уравнения равносильными? - В результате какого преобразования из 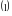 получили получили 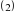 ? ? Изменилась ли ОДЗ уравнения при этом преобразовании? - Рассмотрим группу уравнений б). Равносильны ли эти уравнения? - В результате какого преобразования из 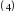 получили получили 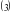 ? ?
- Что произошло с ОДЗ уравнения? - В результате расширения ОДЗ получили уравнение-следствие 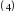 и посторонний корень и посторонний корень  для уравнения для уравнения 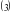 . Значит, расширение ОДЗ уравнения может привести к появлению посторонних корней. . Значит, расширение ОДЗ уравнения может привести к появлению посторонних корней. | Да, 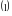 и и 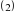 равносильны равносильны
Использовали тождество  нет
Нет, уравнение 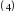 - следствие уравнения - следствие уравнения 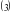
Заменили левую часть уравнения тождественно равным ему выражением
ОДЗ расширилась |
| Задание 2. Равносильны ли следующие уравнения? Назовите преобразование, в результате которого первое уравнение заменено вторым уравнением. 

 - Какие из предложенных уравнений равносильны? - Какие из предложенных уравнений равносильны? - Какие преобразования выполнялись, чтобы от уравнения 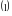 перейти к уравнению перейти к уравнению 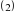 , , 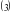 ? ? - То есть в каждом случае прибавили некоторую функцию  . . Сравните область определения функции  в уравнении в уравнении 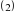 с ОДЗ уравнения с ОДЗ уравнения 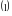 . . - Какое уравнение получили в результате прибавления к обеим частям уравнения 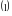 функции функции  ? ? |
Только уравнения 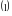 и и 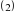
К обеим частям уравнения 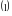 в первом случае прибавили в первом случае прибавили  , во втором случае прибавили , во втором случае прибавили  . .
Функция  определена на ОДЗ уравнения определена на ОДЗ уравнения 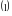 . .
Получим уравнение равносильное 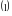 . . |
| Что нового вы сегодня узнали на уроке?
Какую задачу мы поставили в начале урока?
Решили ли мы ее полностью? Поставленную задачу, мы решили частично, ее исследование продолжим на следующих уроках при решении новых видов уравнений. Спасибо за урок, досвиданье.
| Понятия равносильных уравнений, уравнения-следствия, теоремы о равносильности уравнений.
Выделить преобразования, не изменяющие множество корней уравнения, преобразования, ведущие к приобретению и потере корней.
Нет. |
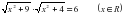 ,
,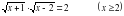 ,
,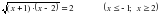 ,
,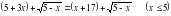 ,
,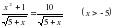
 .
. 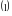
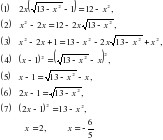
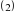 и т.д. к
и т.д. к 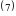 . Проследим, что происходит с корнями уравнения на каждом этапе преобразований. В представленном решении получены два корня уравнения
. Проследим, что происходит с корнями уравнения на каждом этапе преобразований. В представленном решении получены два корня уравнения 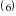 . Проверьте, являются ли числа
. Проверьте, являются ли числа 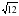 и
и 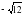 корнями исходного уравнения
корнями исходного уравнения 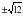 и приобретению постороннего корня
и приобретению постороннего корня 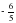 .
. ,
, 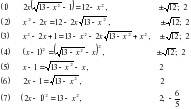
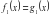 и
и 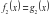 называются равносильными, если множества их корней совпадают.
называются равносильными, если множества их корней совпадают.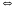 ». Процесс решения уравнения
». Процесс решения уравнения 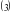
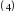 …
…