Рабочая программа Математика 5 и 6 класс (УМК Козлова С.А., Рубин А.Г)

Рабочая программа по предмету «Математика» для основной школы

МБОУ «Калининская СОШ»

5–9-й классы

Программа составлена в соответствии с требованиями Федерального государственного образовательного стандарта основного общего образования и обеспечена УМК для 5–9-го классов авторов С.А. Козловой, А.Г. Рубина, В.Н. Гераськина, В.А. Гусева, П.В. Чулкова.

I. Пояснительная записка

Математика является одним из основных, системообразующих предметов школьного образования. Такое место математики среди школьных предметов обусловливает и её особую роль с точки зрения всестороннего развития личности учащихся. При этом когнитивная составляющая данного курса позволяет обеспечить как требуемый государственным стандартом необходимый уровень математической подготовки, так и повышенный уровень, являющийся достаточным для углубленного изучения предмета.

Математическое образование является обязательной и неотъемлемой частью общего образования на всех ступенях школы.

Без базовой математической подготовки невозможно достичь высокого уровня образования, так как всё больше специальностей связано с непосредственным применением математики. Следовательно, расширяется круг школьников, для которых математика становится профессионально значимым предметом.

Математике принадлежит ведущая роль в формировании алгоритмического мышления, воспитании умения действовать по заданным алгоритмам и конструировать новые. В ходе решения задач основной учебной деятельности на уроках математики развиваются творческая и прикладная стороны мышления.

Обучение математике в основной школе направлено на достижение следующих целей:

1. в направлении личностного развития

• развитие логического и критического мышления, культуры речи, способности к умственному эксперименту;

• формирование у учащихся интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта;

• воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать, самостоятельны решения;

• формирование качеств мышления, необходимых для адаптации в современном информационном обществе;

• развитие интереса к математическому творчеству и математических способностей;

1. в метапредметном направлении

• формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества;

• развитие представлений о математике как форме описания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования;

• формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся осно­вой познавательной культуры, значимой для различных сфер человеческой деятельности;

3) в предметном направлении

• овладение математическими знаниями и умениями, необходимыми для продолжения обучения в старшей школе или иных общеобразовательных учреждениях, изучения смежных дисциплин, применения в повседневной жизни;

• создание фундамента для математического развития, формирования механизмов мышления, характерных для математической деятельности.

Содержание математического образования в основной школе формируется на основе фундаментального ядра школьного математического образования. В программе оно представлено в виде совокупности содержательных разделов, конкретизирующих соответствующие блоки фундаментального ядра применительно к основной школе. Содержание математического образования применительно к основной школе представлено в виде следующих содержа­тельных разделов. Это арифметика; алгебра; функции; ве­роятность и статистика', геометрия. Наряду с этим в со­держание основного общего образования включены два до­полнительных методологических раздела: логика и математика в историческом развитии, что связано с реализацией целей общеинтеллектуального и общекультурно­го развития обучающихся. Содержание каждого из этих разделов разворачивается в содержательно-методическую линию, про­низывающую все основные разделы содержания математичес­кого образования на данной ступени обучения. При этом пер­вая линия — «Логика» — служит цели овладения учащимися некоторыми элементами универсального матема­тического языка, вторая — «Математика в историческом раз­витии» — способствует созданию общекультурного, гуманитар­ного фона изучения курса.

Содержание раздела «Арифметика» служит базой для даль­нейшего изучения учащимися математики, способствует разви­тию их логического мышления, формированию умения поль­зоваться алгоритмами, а также приобретению практических на­выков, необходимых в повседневной жизни. Развитие понятия о числе в основной школе связано с рациональными и ирра­циональными числами, формированием первичных представ­лений о действительном числе.

Содержание раздела «Алгебра» способствует формирова­нию у учащихся математического аппарата для решения задач из разных разделов математики, смежных предметов, окружа­ющей реальности. В задачи изучения алгебры входят также развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики, овладение навыками дедуктивных рассуждений. Преобразова­ние символьных форм вносит специфический вклад в разви­тие воображения учащихся, их способностей к математичес­кому творчеству. В основной школе материал группируется вокруг рациональных выражений, а вопросы, связанные с ир­рациональными выражениями, с тригонометрическими функ­циями и преобразованиями, входят в содержание курса мате­матики на старшей ступени обучения в школе.

Содержание раздела «Функции» нацелено на получение школьниками конкретных знаний о функции как важнейшей математической модели для описания и исследования разно­образных процессов. Изучение этого материала способствует развитию у учащихся умения использовать различные языки математики (словесный, символический, графический), вносит вклад в формирование представлений о роли математики в развитии цивилизации и культуры.

Раздел «Вероятность и статистика» — обязательный компонент школьного образования, усиливающий его прикладное и практическое значение. Этот материал необходим, прежде всего, для формирования у учащихся функциональной грамотности — умения воспринимать и критически анализиро­вать информацию, представленную в различных формах, по­нимать вероятностный характер многих реальных зависимос­тей, производить простейшие вероятностные расчеты. Изуче­ние основ комбинаторики позволит учащемуся осуществлять рассмотрение случаев, перебор и подсчет числа вариантов, в том числе в простейших прикладных задачах. При изучении статистики и вероятности обогащаются представления о современной картине мира и методах его ис­следования, формируется понимание роли статистики как ис­точника социально значимой информации, и закладываются основы вероятностного мышления.

Цель содержания раздела «Геометрия» — развить у учащих­ся пространственное воображение и логическое мышление пу­тем систематического изучения свойств геометрических фигур на плоскости и в пространстве и применения этих свойств при решении задач вычислительного и конструктивного ха­рактера. Существенная роль при этом отводится развитию ге­ометрической интуиции. Сочетание наглядности со стро­гостью является неотъемлемой частью геометрических знаний. Особенностью раздела «Логика и множества» является то, что представленный в нем материал преимущественно изуча­ется при рассмотрении различных вопросов курса. Соответствующий материал нацелен на математическое развитие учащихся, формирование у них умения точно, сжато и ясно из­лагать мысли в устной и письменной речи.

Раздел «Математика в историческом развитии» предназна­чен для формирования представлений о математике как час­ти человеческой культуры, для общего развития школьников, для создания культурно-исторической среды обучения. На не­го не выделяется специальных уроков, усвоение его не конт­ролируется, но содержание этого раздела органично присутствует в учебном процессе как своего рода гуманитарный фон при рассмотрении проблематики основного содержания мате­матического образования.

В основу настоящей программы положены педагогические и дидактические принципы вариативного развивающего образования, изложенные в концепции образовательной программы «Школа 2100».

А. Личностно ориентированные принципы: принцип адаптивности; принцип развития; принцип комфортности процесса обучения.

Б. Культурно ориентированные принципы: принцип целостной картины мира; принцип целостности содержания образования; принцип систематичности; принцип смыслового отношения к миру; принцип ориентировочной функции знаний; принцип опоры на культуру как мировоззрение и как культурный стереотип.

В. Деятельностно ориентированные принципы: принцип обучения деятельности; принцип управляемого перехода от деятельности в учебной ситуации к деятельности в жизненной ситуации; принцип перехода от совместной учебно-познавательной деятельности к самостоятельной деятельности учащегося (зона ближайшего развития); принцип опоры на процессы спонтанного развития; принцип формирования потребности в творчестве и умений творчества.

Настоящая программа по математике для основной школы является логическим продолжением программы для начальной школы (авторы Т.Е. Демидова, С.А. Козлова, А.П. Тонких) и составляет вместе с ней описание непрерывного школьного курса математики.

В основе построения данного курса лежит идея гуманизации обучения, соответствующая современным представлениям о целях школьного образования и уделяющая особое внимание личности ученика, его интересам и способностям. Предлагаемый курс позволяет обеспечить формирование как предметных умений, так и универсальных учебных действий школьников, а также способствует достижению определённых во ФГОС личностных результатов, которые в дальнейшем позволят учащимся применять полученные знания и умения для решения различных жизненных задач.

II. Нормативно-правовая база образовательной программы:

• Закон РФ «Об образовании» от 29.12.2012 № 273;

• Типовое положением об общеобразовательном учреждении (постановление Правительства РФ от 19.03.2001, № 196);

• Приказ Министерства образования и науки Российской Федерации № 1897 от 17 декабря 2010г. «Об утверждении и введении в действие федерального государственного образовательного стандарта основного общего образования»

• Федеральный государственный образовательный стандарт основного общего образования;

• Концепция духовно-нравственного развития и воспитания личности гражданина России;

• Примерная основная образовательная программа ООО А.М.Кондакова.

• Примерные программы по учебным предметам;   

• Федеральный перечень учебников, рекомендованных Министерством образования и науки Российской Федерации к использованию в образовательном процессе  в общеобразовательных учреждениях, на 2013 – 2014;

• СанПиН 2.4.2.2821-10 «Санитарно-эпидемиологические требования к условиям и организации обучения в общеобразовательных учреждениях;

• Устав МБОУ «Калининская СОШ»;

• Программа развития школы;

• Локальные акты школы.

III. Общая характеристика учебного предмета «Математика»

Настоящая программа по математике для основной школы является логическим продолжением программы для начальной школы и вместе с ней составляет описание непрерывного курса математики с 1-го по 9-й класс общеобразовательной школы.

В основе содержания обучения математике лежит овладение учащимися следующими видами компетенций: предметной, коммуникативной, организационной и общекультурной. В соответствии с этими видами компетенций нами выделены главные содержательно-целевые направления (линии) развития учащихся средствами предмета «Математика».

Предметная компетенция. Под предметной компетенцией понимается осведомлённость школьников о системе основных математических представлений и овладение ими необходимыми предметными умениями. Формируются следующие образующие эту компетенцию представления: о математическом языке как средстве выражения математических законов, закономерностей и т.д.; о математическом моделировании как одном из важных методов познания мира. Формируются следующие образующие эту компетенцию умения: создавать простейшие математические модели, работать с ними и интерпретировать полученные результаты; приобретать и систематизировать знания о способах решения математических задач, а также применять эти знания и умения для решения многих жизненных задач.

Коммуникативная компетенция. Под коммуникативной компетенцией понимается сформированность умения ясно и чётко излагать свои мысли, строить аргументированные рассуждения, вести диалог, воспринимая точку зрения собеседника и в то же время подвергая её критическому анализу, отстаивать (при необходимости) свою точку зрения, выстраивая систему аргументации. Формируются образующие эту компетенцию умения, а также умения извлекать информацию из разного рода источников, преобразовывая её при необходимости в другие формы (тексты, таблицы, схемы и т.д.).

Организационная компетенция. Под организационной компетенцией понимается сформированность умения самостоятельно находить и присваивать необходимые учащимся новые знания. Формируются следующие образующие эту компетенцию умения: самостоятельно ставить учебную задачу (цель), разбивать её на составные части, на которых будет основываться процесс её решения, анализировать результат действия, выявлять допущенные ошибки и неточности, исправлять их и представлять полученный результат в форме, легко доступной для восприятия других людей.

Общекультурная компетенция. Под общекультурной компетенцией понимается осведомленность школьников о математике как элементе общечеловеческой культуры, её месте в системе других наук, а также её роли в развитии представлений человечества о целостной картине мира. Формируются следующие образующие эту компетенцию представления: об уровне развития математики на разных исторических этапах; о высокой практической значимости математики с точки зрения создания и развития материальной культуры человечества, а также о важной роли математики с точки зрения формировании таких важнейших черт личности, как независимость и критичность мышления, воля и настойчивость в достижении цели.

IV. Описание места учебного предмета «Математика» в учебном плане

В соответствии с требованиями Федерального государственного образовательного стандарта основного общего образования предмет «Математика» изучается с 5-го по 9-й класс в виде следующих учебных курсов: 5–6 класс – «Математика», 7–9 класс – «Алгебра» и «Геометрия». Общее количество уроков в неделю с 5 по 9 класс составляет 25 часов (5–6 класс – по 5 часов в неделю, 7–9 класс – алгебра по 3 часа в неделю, геометрия – по 2 часа в неделю.)

V.Личностные, метапредметные и предметные результаты освоения учебного

предмета «Математика»

Программа позволяет добиваться следующих результатов освоения образовательной программы основного общего об­разования

В личностном направлении:

• ЛР1- ответственное отношение к учению;

• ЛР2- готовность и спо­собность обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию;

• ЛР3- умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;

• ЛР4- начальные навыки адаптации в динамично изменяющемся мире;

• ЛР5- экологическая культура: ценностное отношение к природному миру, готовность следовать нормам природоохранного, здоровьесберегающего поведения;

• ЛР6- формирование способности к эмоциональному вос­приятию математических объектов, задач, решений, рассуж­дений;

• ЛР7- умение контролировать процесс и результат учебной ма­тематической деятельности;

• ЛР-первоначальные представления о математической науке как сфере человеческой деятельности, об этапах её развития, о её значимости для развития цивилизации;

• ЛРР9-коммуникативная компетентность в об­щении и сотрудничестве со сверстниками в образовательной, учебно-исследовательской, творче­ской и других видах деятельности;

• Л10- критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;

• ЛР11- креативность мышления, инициативы, находчивости, активности при решении арифметических задач.

В метапредметном направлении:

• МР1- формулировать и удерживать учебную задачу;

• МР2- выбирать действия в соответствии с поставленной задачей и условиями её реализации;

• МР3-планировать пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;

• МР4- предвидеть уровень усвоения знаний, его временных характеристик;

• МР5- составлять план и последовательность действий;

• МР6- осуществлять контроль по образцу и вносить не­обходимые коррективы;

• МР7- адекватно оценивать правильность или ошибочность выполнения учебной задачи, её объективную трудность и собственные возможности её решения;

• МР8- сличать способ действия и его результат с заданным эталоном с целью обнаружения отклонений и отличий от эталона;

• МР9- определять последовательность промежуточных целей и соответствующих им действий с учётом конечного результата;

• МР10- предвидеть возможности получения конкретного результата при решении задач;

• МР11- осуществлять констатирующий и прогнозирующий контроль по результату и по способу действия;

• МР12-выделять и формулировать то, что усвоено и что нужно усвоить, определять качество и уровень усвоения;

• МР13- концентрировать волю для преодоления интеллектуальных затруднений и физических препятствий;

• МР14- самостоятельно выделять и формулировать познавательную цель;

• МР15- использовать общие приёмы решения задач;

• МР16- применять правила и пользоваться инструкциями и освоенными закономерностями;

• МР17- осуществлять смысловое чтение;

• МР18- создавать, применять и преобразовывать знаково-символические средства, модели и схемы для решения задач;

• МР19- самостоятельно ставить цели, выбирать и соз­давать алгоритмы для решения учебных математических про­блем;

• МР20-понимать сущность алгоритмических предписаний и уметь действовать в соответствии с предложенным ал­горитмом;

• МР21- понимать и использовать математические сред­ства наглядности (рисунки, чертежи, схемы и др.) для иллю­страции, интерпретации, аргументации;

• МР22- находить в различных источниках информа­цию, необходимую для решения математических проблем, и представлять её в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации;

• МР23- устанавливать причинно-следственные связи; строить логические рассуждения, умозаключения (индуктив­ные, дедуктивные и по аналогии) и выводы;

• МР24- формировать учебную и общепользовательскую компе­тентности в области использования информационно-комму­никационных технологий (ИКТ-компетент­ности);

• МР25-видеть математическую задачу в других дисциплинах, в окружающей жизни;

• МР26- выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки;

• МР27- планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;

• МР28- выбирать наиболее рациональные и эффективные способы решения задач;

• МР29-интерпретировать информации (структурировать, переводить сплошной текст в таблицу, презентовать полученную информацию, в том числе с помощью ИКТ);

• МР30-оценивать информацию (критическая оценка, оценка достоверности);

• МР31- организовывать учебное сотруд­ничество и совместную деятельность с учителем и сверстни­ками: определять цели, распределять функции и роли участ­ников;

• МР32- взаимодействовать и находить общие способы работы; работать в группе: находить общее решение и разре­шать конфликты на основе согласования позиций и учёта ин­тересов; слушать партнёра; формулировать, аргументировать и отстаивать своё мнение;

• МР33- прогнозировать возникновение конфликтов при наличии разных точек зрения;

• МР34- разрешать конфликты на основе учёта интересов и позиций всех участников;

• МР35- координировать и принимать различные позиции во взаимодействии;

• МР36- аргументировать свою позицию и координировать её с позициями партнёров в сотрудничестве при выработке общего решения в совместной деятельности.

В предметном направлении:

• ПР1-работать с математическим текстом (структу­рирование, извлечение необходимой информации), точно и грамотно выражать свои мысли в устной и письменной речи, применяя математическую терминологию и символику, ис­пользовать различные языки математики (словесный, симво­лический, графический), обосновывать суждения, проводить классификацию;

• ПР2- владеть базовым понятийным аппаратом: иметь представление о числе, дроби, об основных гео­метрических объектах (точка, прямая, ломаная, угол, мно­гоугольник, многогранник, круг, окружность);

• ПР3- выполнять арифметические преобразования, применять их для решения учебных математических задач;

• ПР4- пользоваться изученными математическими формулами;

• ПР5- самостоятельно приобретать и применять знания в различных ситуациях для решения не­сложных практических задач, в том числе с использованием при необходимости справочных мате­риалов, калькулятора и компьютера;

• ПР6- пользоваться предметным указателем энциклопедий и справочников для нахождения ин­формации;

• ПР7- знать основные способы представления и анализа ста­тистических данных; уметь решать задачи с помощью пере­бора возможных вариантов;

• ПР8- выполнять арифметические преобразования выражений, применять их для решения учебных математических задач и задач, возникающих в смежных учеб­ных предметах;

• ПР9- применять изученные понятия, результаты и ме­тоды при решении задач из различных разделов курса, в том числе задач, не сводящихся к непосредственному применению известных алгоритмов;

• ПР10- самостоятельно действовать в ситуации неопределённости при решении актуальных для них проблем, а также самостоятельно интерпретировать результаты решения задач с учетом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений.

VI. Предметными результатами изучения предмета «Математика» являются следующие умения.

5-й класс

Использовать при решении математических задач, их обосновании и проверке найденного решения знание:

• названий и последовательности чисел в натуральном ряду в пределах 1 000 000 (с какого числа начинается этот ряд, как образуется каждое следующее число в этом ряду);

• как образуется каждая следующая счётная единица;

• названия и последовательность разрядов в записи числа;

• названия и последовательность первых трёх классов;

• сколько разрядов содержится в каждом классе;

• соотношение между разрядами;

• сколько единиц каждого класса содержится в записи числа;

• как устроена позиционная десятичная система счисления;

• единицы измерения величин (длина, масса, время, площадь), соотношения между ними;

• функциональной связи между группами величин (цена, количество, стоимость; скорость, время, расстояние; производительность труда, время работы, работа).

Выполнять устные вычисления (в пределах 1 000 000) в случаях, сводимых к вычислениям в пределах 100, и письменные вычисления в остальных случаях; выполнять проверку правильности вычислений;

• выполнять умножение и деление с 1 000;

• вычислять значения числовых выражений, содержащих 3–4 действия со скобками и без них;

• раскладывать натуральное число на простые множители;

• находить наибольший общий делитель и наименьшее общее кратное нескольких чисел;

• решать простые и составные текстовые задачи;

• выписывать множество всевозможных результатов (исходов) простейших случайных экспериментов;

• находить вероятности простейших случайных событий;

• решать удобным для себя способом (в том числе и с помощью таблиц и графов) комбинаторные задачи: на перестановку из трёх элементов, правило произведения, установление числа пар на множестве из 3–5 элементов;

• решать удобным для себя способом (в том числе и с помощью таблиц и графов) логические задачи, содержащие не более трёх высказываний;

• читать информацию, записанную с помощью линейных, столбчатых и круговых диаграмм;

• строить простейшие линейные, столбчатые и круговые диаграммы;

- находить решения «жизненных» (компетентностных) задач, в которых используются математические средства;

- создавать продукт (результат проектной деятельности), для изучения и описания которого используются математические средства.

6-й класс

Использовать при решении математических задач, их обосновании и проверке найденного решения знание о:

• десятичных дробях и правилах действий с ними;

• отношениях и пропорциях; основном свойстве пропорции;

• прямой и обратной пропорциональных зависимостях и их свойствах;

• процентах;

• целых и дробных отрицательных числах; рациональных числах;

• правиле сравнения рациональных чисел;

• правилах выполнения операций над рациональными числами; свойствах операций.

– Сравнивать десятичные дроби;

• выполнять операции над десятичными дробями;

• преобразовывать десятичную дробь в обыкновенную и наоборот;

• округлять целые числа и десятичные дроби;

• находить приближённые значения величин с недостатком и избытком;

• выполнять приближённые вычисления и оценку числового выражения;

• делить число в данном отношении;

• находить неизвестный член пропорции;

• находить данное количество процентов от числа и число по известному количеству процентов от него;

• находить, сколько процентов одно число составляет от другого;

• увеличивать и уменьшать число на данное количество процентов;

• решать текстовые задачи на отношения, пропорции и проценты;

• сравнивать два рациональных числа;

• выполнять операции над рациональными числами, использовать свойства операций для упрощения вычислений;

• решать комбинаторные задачи с помощью правила умножения;

• находить вероятности простейших случайных событий;

• решать простейшие задачи на осевую и центральную симметрию;

• решать простейшие задачи на разрезание и составление геометрических фигур;

• находить решения «жизненных» (компетентностных) задач, в которых используются математические средства;

• создавать продукт (результат проектной деятельности), для изучения и описания которого используются математические средства.

7-й класс.

Алгебра

Использовать при решении математических задач, их обосновании и проверке найденного решения знание о:

• натуральных, целых, рациональных, иррациональных, действительных числах;

• степени с натуральными показателями и их свойствах;

• одночленах и правилах действий с ними;

• многочленах и правилах действий с ними;

• формулах сокращённого умножения;

• тождествах; методах доказательства тождеств;

• линейных уравнениях с одной неизвестной и методах их решения;

• системах двух линейных уравнений с двумя неизвестными и методах их решения.

• Выполнять действия с одночленами и многочленами;

• узнавать в выражениях формулы сокращённого умножения и применять их;

• раскладывать многочлены на множители;

• выполнять тождественные преобразования целых алгебраических выражений;

• доказывать простейшие тождества;

• находить число сочетаний и число размещений;

• решать линейные уравнения с одной неизвестной;

• решать системы двух линейных уравнений с двумя неизвестными методом подстановки и методом алгебраического сложения;

• решать текстовые задачи с помощью линейных уравнений и систем;

• находить решения «жизненных» (компетентностных) задач, в которых используются математические средства;

• создавать продукт (результат проектной деятельности), для изучения и описания которого используются математические средства.

7-й класс.

Геометрия

Использовать при решении математических задач, их обосновании и проверке найденного решения знание о:

• основных геометрических понятиях: точка, прямая, плоскость, луч, отрезок, ломаная, многоугольник;

• определении угла, биссектрисы угла, смежных и вертикальных углов;

• свойствах смежных и вертикальных углов;

• определении равенства геометрических фигур; признаках равенства треугольников;

• геометрических местах точек; биссектрисе угла и серединном перпендикуляре к отрезку как геометрических местах точек;

• определении параллельных прямых; признаках и свойствах параллельных прямых;

• аксиоме параллельности и её краткой истории;

• формуле суммы углов треугольника;

• определении и свойствах средней линии треугольника;

• теореме Фалеса.

• Применять свойства смежных и вертикальных углов при решении задач;

• находить в конкретных ситуациях равные треугольники и доказывать их равенство;

• устанавливать параллельность прямых и применять свойства параллельных прямых;

• применять теорему о сумме углов треугольника;

• использовать теорему о средней линии треугольника и теорему Фалеса при решении задач;

• находить решения «жизненных» (компетентностных) задач, в которых используются математические средства;

• создавать продукт (результат проектной деятельности), для изучения и описания которого используются математические средства.

8-й класс.

Алгебра

Использовать при решении математических задач, их обосновании и проверке найденного решения знание о:

• алгебраической дроби; основном свойстве дроби;

• правилах действий с алгебраическими дробями;

• степенях с целыми показателями и их свойствах;

• стандартном виде числа;

• функциях 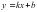, , 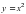, 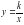их свойствах и графиках;

• понятии квадратного корня и арифметического квадратного корня;

• свойствах арифметических квадратных корней;

• функции 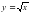, её свойствах и графике;

• формуле для корней квадратного уравнения;

• теореме Виета для приведённого и общего квадратного уравнения;

• основных методах решения целых рациональных уравнений: методе разложения на множители и методе замены неизвестной;

• методе решения дробных рациональных уравнений;

• основных методах решения систем рациональных уравнений.

• Сокращать алгебраические дроби;

• выполнять арифметические действия с алгебраическими дробями;

• использовать свойства степеней с целыми показателями при решении задач;

• записывать числа в стандартном виде;

• выполнять тождественные преобразования рациональных выражений;

• строить графики функций 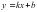, , 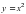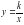и использовать их свойства при решении задач;

• вычислять арифметические квадратные корни;

• применять свойства арифметических квадратных корней при решении задач;

• строить график функции 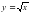и использовать его свойства при решении задач;

• решать квадратные уравнения;

• применять теорему Виета при решении задач;

• решать целые рациональные уравнения методом разложения на множители и методом замены неизвестной;

• решать дробные уравнения;

• решать системы рациональных уравнений;

• решать текстовые задачи с помощью квадратных и рациональных уравнений и их систем;

• находить решения «жизненных» (компетентностных) задач, в которых используются математические средства;

• создавать продукт (результат проектной деятельности), для изучения и описания которого используются математические средства.

8-й класс.

Геометрия

Использовать при решении математических задач, их обосновании и проверке найденного решения знание о:

• определении параллелограмма, ромба, прямоугольника, квадрата; их свойствах и признаках;

• определении трапеции; элементах трапеции; теореме о средней линии трапеции;

• определении окружности, круга и их элементов;

• теореме об измерении углов, связанных с окружностью;

• определении и свойствах касательных к окружности; теореме о равенстве двух касательных, проведённых из одной точки;

• определении вписанной и описанной окружностей, их свойствах;

• определении тригонометрические функции острого угла, основных соотношений между ними;

• приёмах решения прямоугольных треугольников;

• тригонометрических функциях углов от 0 до 180°;

• теореме косинусов и теореме синусов;

• приёмах решения произвольных треугольников;

• формулах для площади треугольника, параллелограмма, трапеции;

• теореме Пифагора.

• Применять признаки и свойства параллелограмма, ромба, прямоугольника, квадрата при решении задач;

• решать простейшие задачи на трапецию;

• находить градусную меру углов, связанных с окружностью; устанавливать их равенство;

• применять свойства касательных к окружности при решении задач;

• решать задачи на вписанную и описанную окружность;

• выполнять основные геометрические построения с помощью циркуля и линейки;

• находить значения тригонометрических функций острого угла через стороны прямоугольного треугольника;

• применять соотношения между тригонометрическими функциями при решении задач; в частности, по значению одной из функций находить значения всех остальных;

• решать прямоугольные треугольники;

• сводить работу с тригонометрическими функциями углов от 0 до 180° к случаю острых углов;

• применять теорему косинусов и теорему синусов при решении задач;

• решать произвольные треугольники;

• находить площади треугольников, параллелограммов, трапеций;

• применять теорему Пифагора при решении задач;

• находить простейшие геометрические вероятности;

• находить решения «жизненных» (компетентностных) задач, в которых используются математические средства;

• создавать продукт (результат проектной деятельности), для изучения и описания которого используются математические средства.

9-й класс.

Алгебра

Использовать при решении математических задач, их обосновании и проверке найденного решения знание о:

• свойствах числовых неравенств;

• методах решения линейных неравенств;

• свойствах квадратичной функции;

• методах решения квадратных неравенств;

• методе интервалов для решения рациональных неравенств;

• методах решения систем неравенств;

• свойствах и графике функции 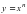при натуральном n;

• определении и свойствах корней степени n;

• степенях с рациональными показателями и их свойствах;

• определении и основных свойствах арифметической прогрессии; формуле для нахождения суммы её нескольких первых членов;

• определении и основных свойствах геометрической прогрессии; формуле для нахождения суммы её нескольких первых членов;

• формуле для суммы бесконечной геометрической прогрессии со знаменателем, меньшим по модулю единицы.

• Использовать свойства числовых неравенств для преобразования неравенств;

• доказывать простейшие неравенства;

• решать линейные неравенства;

• строить график квадратичной функции и использовать его при решении задач;

• решать квадратные неравенства;

• решать рациональные неравенства методом интервалов;

• решать системы неравенств;

• строить график функции 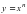при натуральном n и использовать его при решении задач;

• находить корни степени n;

• использовать свойства корней степени n при тождественных преобразованиях;

• находить значения степеней с рациональными показателями;

• решать основные задачи на арифметическую и геометрическую прогрессии;

• находить сумму бесконечной геометрической прогрессии со знаменателем, меньшим по модулю единицы;

• находить решения «жизненных» (компетентностных) задач, в которых используются математические средства;

• создавать продукт (результат проектной деятельности), для изучения и описания которого используются математические средства.

9-й класс.

Геометрия

Использовать при решении математических задач, их обосновании и проверке найденного решения знание о:

• признаках подобия треугольников;

• теореме о пропорциональных отрезках;

• свойстве биссектрисы треугольника;

• пропорциональных отрезках в прямоугольном треугольнике;

• пропорциональных отрезках в круге;

• теореме об отношении площадей подобных многоугольников;

• свойствах правильных многоугольников; связи между стороной правильного многоугольника и радиусами вписанного и описанного кругов;

• определении длины окружности и формуле для её вычисления;

• формуле площади правильного многоугольника;

• определении площади круга и формуле для её вычисления; формуле для вычисления площадей частей круга;

• правиле нахождения суммы и разности векторов, произведения вектора на скаляр; свойства этих операций;

• определении координат вектора и методах их нахождения;

• правиле выполнений операций над векторами в координатной форме;

• определении скалярного произведения векторов и формуле для его нахождения;

• связи между координатами векторов и координатами точек;

• векторным и координатным методах решения геометрических задач.

• формулах объёма основных пространственных геометрических фигур: параллелепипеда, куба, шара, цилиндра, конуса.

• Применять признаки подобия треугольников при решении задач;

• решать простейшие задачи на пропорциональные отрезки;

• решать простейшие задачи на правильные многоугольники;

• находить длину окружности, площадь круга и его частей;

• выполнять операции над векторами в геометрической и координатной форме;

• находить скалярное произведение векторов и применять его для нахождения различных геометрических величин;

• решать геометрические задачи векторным и координатным методом;

• применять геометрические преобразования плоскости при решении геометрических задач;

• находить объёмы основных пространственных геометрических фигур: параллелепипеда, куба, шара, цилиндра, конуса;

• находить решения «жизненных» (компетентностных) задач, в которых используются математические средства;

• создавать продукт (результат проектной деятельности), для изучения и описания которого используются математические средства.

VII. Содержание учебного предмета «Математика»

5-й класс

Математика (170 часов)

Повторение, обобщение и систематизация материала, изученного в начальной школе.

Понятие натурального числа, числовой луч, координата точки на луче, десятичная система счисления. Чтение и запись чисел. Классы и разряды. Сравнение чисел. Арифметические операции. Устные и письменные приёмы вычислений. Понятие дробного числа. Сравнение дробей с одинаковыми числителями либо с одинаковыми знаменателями. Нахождение части числа. Нахождение числа по его части. Какую часть одно число составляет от другого. Сложение и вычитание дробей с одинаковыми знаменателями. Вычисление значений числовых выражений (со скобками и без них) на основе знания правила о порядке выполнения действий и знания свойств арифметических операций.

Делимость натуральных чисел.

Свойства делимости. Признаки делимости. Простые и составные числа. Делители и кратные. Разложение на простые множители. Наибольший общий делитель, наименьшее общее кратное; методы их нахождения.

Обыкновенные дроби.

Понятие дроби. Нахождение части от целого и целого по его части. Натуральные числа и дроби. Основное свойство дроби. Приведение дробей к общему знаменателю. Понятие неправильной и смешанной дроби. Преобразование неправильной дроби в смешанную и наоборот. Сравнение дробей.

Действия с дробями и их свойства.

Сложение дробей. Свойства сложения. Вычитание дробей. Умножение дробей. Свойства умножения. Деление дробей. Сложение и вычитание смешанных дробей. Умножение и деление смешанных дробей.

Геометрические фигуры.

Углы. Измерение углов. Ломаные и многоугольники. Треугольники и их виды. Равенство геометрических фигур. Окружность и круг. Центральные углы. Площадь прямоугольника. Площадь прямоугольного треугольника. Единицы измерения площадей. Объёмные тела. Прямоугольный параллелепипед. Объём прямоугольного параллелепипеда. Единицы измерения объёма.

Текстовые задачи.

Различные модели текстовых задач: выражение, уравнение, схема, таблица.

Задачи на уравнивание. Задачи на части. Задачи на работу. Задачи с дробными числами. Задачи с альтернативным условием.

Задачи на движение и их различные виды. Одновременное движение по числовому лучу. Встречное движение и движение в противоположном направлении. Движение вдогонку. Движение с отставанием. Движение по реке.

Элементы логики, статистики, комбинаторики, теории вероятностей.

Сбор и обработка статистической информации о явлениях окружающей действительности. Опросы общественного мнения как сбор и обработка статистической информации.

Решение простейших логических задач.

Круговые диаграммы. Чтение информации, содержащейся в круговой диаграмме. Построение круговых диаграмм.

Решение простейших комбинаторных задач.

Понятие о вероятности случайного события.

Занимательные и нестандартные задачи.

Принцип Дирихле.

Математические игры.

Итоговое повторение.

6-й класс

Математика (170 часов)

Десятичные дроби.

Понятие десятичной дроби. Сложение и вычитание десятичных дробей. Деление и умножение десятичной дроби на натуральную степень числа 10. Умножение десятичных дробей. Деление десятичных дробей. Приближённые вычисления с десятичными дробями. Преобразование десятичных дробей в обыкновенные и наоборот.

Пропорции и проценты.

Отношение. Деление числа в данном отношении. Пропорции, основные свойства пропорций. Прямая и обратная пропорциональные зависимости. Проценты. Нахождение процентов от числа и числа по известному количеству процентов от него. Процентное отношение двух чисел. Увеличение и уменьшение числа на данное количество процентов. Решение задач на проценты.

Положительные и отрицательные числа.

Целые отрицательные числа. Модуль числа. Изображение целых чисел на числовой оси. Сравнение целых чисел. Арифметические операции над целыми числами, законы операций. Отрицательные дроби. Рациональные числа. Изображение рациональных чисел на числовой оси. Арифметические операции над рациональными числами, законы операций. Бесконечные периодические десятичные дроби. Бесконечные непериодические десятичные дроби. Иррациональные числа. Действительные числа. Изображение действительных чисел на числовой оси.

Элементы геометрии.

Симметрия относительной оси и относительно точки. Задачи на разрезание и составление фигур. Геометрия на клетчатой бумаге.

Элементы логики, статистики, комбинаторики, теории вероятностей.

Решение логических задач. Решение комбинаторных задач с помощью правила умножения. Нахождение вероятностей простейших случайных событий.

Итоговое повторение.

7-й класс

Алгебра (102 часа)

Повторение, обобщение и систематизация представлений о числе, изученных в курсе математики 5 – 6 классов.

Числа натуральные, целые, рациональные, иррациональные, действительные.

Одночлены и операции над ними.

Степени с натуральными показателями и их свойства. Одночлен, стандартный вид одночлена. Подобные одночлены, сложение и вычитание одночленов. Умножение одночленов и возведение одночлена в натуральную степень. Деление одночленов.

Многочлены.

Понятие многочлена, стандартный вид многочлена. Сумма и разность многочленов. Произведение многочлена на одночлен и произведение многочленов. Формулы сокращённого умножения. Деление многочлена на одночлен. Разложение многочлена на множители. Понятие о тождествах и методах их доказательства.

Линейные уравнения.

Линейные уравнения, метод их решения. Системы двух линейных уравнений с двумя неизвестными, их решение методом подстановки и методом алгебраического сложения уравнений. Решение текстовых задач с помощью линейных уравнений и систем.

Элементы логики, статистики, комбинаторики, теории вероятностей.

Простейшие формулы комбинаторики: число сочетаний и число размещений. Их применение при нахождении вероятностей случайных событий.

Итоговое повторение.

7-й класс

Геометрия (68 часов)

Основные понятия геометрии.

Точка, прямая, плоскость. Луч, отрезок, ломаная, многоугольник. Угол, биссектриса угла. Смежные и вертикальные углы. Перпендикулярные прямые. Расстояние от точки до прямой.

Признаки равенства треугольников.

Треугольники. Медианы, биссектрисы, высоты треугольника. Признаки равенства треугольников. Признаки равенства прямоугольных треугольников. Геометрические места точек. Биссектриса угла как геометрическое место точек, равноудалённых от сторон угла. Серединный перпендикуляр к отрезку как геометрическое место точек, равноудалённых от концов отрезка.

Параллельность.

Параллельные прямые. Признаки и свойства параллельных прямых. Аксиома параллельности. Сумма углов треугольника. Средняя линия треугольника. Теорема Фалеса.

Итоговое повторение.

8-й класс

Алгебра (102 часа)

Алгебраические дроби.

Основное свойство дроби. Сокращение дробей. Арифметические действия с дробями. Понятие степени с целым отрицательным показателем, свойства степеней с целыми показателями. Стандартный вид числа. Рациональные выражения. Тождественные преобразования рациональных выражений.

Понятие о функциях.

Основные понятия. Функции 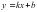, , 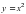, 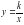их свойства и графики.

Квадратные корни.

Понятие квадратного корня, арифметический квадратный корень. Свойства арифметических квадратных корней. Функция 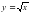, её свойства и график.

Квадратные уравнения.

Квадратный трёхчлен. Неполные квадратные уравнения. Формула для корней квадратного уравнения. Теорема Виета. Решение текстовых задач с помощью квадратных уравнений.

Рациональные уравнения и системы уравнений.

Целые рациональные уравнения: метод разложения на множители левой части при нулевой правой части и метод замены неизвестной. Дробные уравнения, сведение к целым уравнениям и необходимость проверки. Системы рациональных уравнений и основные приёмы их решения. Решение текстовых задач с помощью рациональных уравнений и систем.

Итоговое повторение.

8-й класс

Геометрия (68 часов)

Четырёхугольники.

Параллелограмм. Свойства и признаки параллелограмма. Ромб, прямоугольник, квадрат. Трапеция. Средняя линия трапеции. Равнобедренная трапеция.

Окружность.

Измерение углов, связанных с окружностью. Касательная к окружности, свойства касательных. Вписанная и описанная окружности.

Основные задачи на построение. Построение биссектрисы угла. Построение треугольника по трём элементам. Построение прямой, проходящей через данную точку и перпендикулярной (параллельной) данной прямой. Деление отрезка в данном отношении.

Элементы тригонометрии.

Тригонометрические функции острого угла, основные соотношения между ними. Решение прямоугольных треугольников. Тригонометрические функции углов от 0 до 180°. Теорема косинусов и теорема синусов. Решение треугольников.

Площади многоугольников.

Формулы для площади треугольника, параллелограмма, трапеции. Теорема Пифагора.

Элементы логики, статистики, комбинаторики, теории вероятностей.

Определения, доказательства, аксиомы и теоремы; следствия из теорем. Понятие об аксиоматике и аксиоматическом построении геометрии.

Представление о геометрической вероятности.

Итоговое повторение.

9-й класс

Алгебра (102 часа)

Неравенства и системы неравенств.

Числовые неравенства и их свойства. Понятие о доказательстве неравенств. Неравенства с переменной. Решение линейных неравенств и их систем. Квадратичная функция, её свойства и график. Решение квадратных неравенств. Решение рациональных неравенств методом интервалов. Системы рациональных неравенств.

Степень с рациональным показателем.

Функция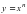 при натуральном n, её свойства и график. Корень степени n, особенности чётных и нечётных n. Арифметический корень. Свойства корней. Степени с рациональными показателями, их свойства. Тождественные преобразования иррациональных выражений.

Арифметическая и геометрическая прогрессии.

Понятие числовой последовательности. Арифметическая прогрессия, её основные свойства. Геометрическая прогрессия, её основные свойства. Бесконечная геометрическая прогрессия со знаменателем, меньшим по модулю единицы. Решение задач на прогрессии.

Итоговое повторение.

9-й класс

Геометрия (68 часов)

Подобие. Подобные многоугольники. Признаки подобия треугольников. Теорема о пропорциональных отрезках. Свойство биссектрисы треугольника. Пропорциональные отрезки в прямоугольном треугольнике. Пропорциональные отрезки в круге. Площади подобных многоугольников.

Длина окружности и площадь круга. Правильные многоугольники, их свойства. Связь между стороной правильного многоугольника и радиусами вписанного и описанного кругов. Длина окружности. Площадь правильного многоугольника. Площадь круга и его частей.

Векторы и координаты.

Понятие о векторах. Сумма и разность векторов, умножение вектора на скаляр. Разложение вектора по двум неколлинеарным векторам. Координаты вектора. Скалярное произведение векторов. Декартовы координаты на плоскости. Уравнение линии. Связь между координатами векторов и координатами точек. Векторный и координатный методы решения геометрических задач.

Геометрические преобразования плоскости. Понятие о движениях плоскости. Осевая и центральная симметрии. Параллельный перенос. Поворот. Понятие о гомотетии. Использование геометрических преобразований при решении задач.

Элементы стереометрии. Формулы объёма основных пространственных геометрических фигур: параллелепипеда, куба, шара, цилиндра, конуса. Правильные многогранники.

Итоговое повторение.

IX. Критерии и нормы оценки ЗУН обучающихся

1. Оценка письменных контрольных работ обучающихся по математике.

Ответ оценивается отметкой «5», если:

• работа выполнена полностью;

• в логических рассуждениях и обосновании решения нет пробелов и ошибок;

• в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).

Отметка «4» ставится в следующих случаях:

• работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);

• допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).

Отметка «3» ставится, если:

• допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.

Отметка «2» ставится, если:

• допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.

Отметка «1» ставится, если:

• работа показала полное отсутствие у обучающегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.

2.Оценка устных ответов обучающихся по математике.

Ответ оценивается отметкой «5», если ученик:

• полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;

• изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;

• правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;

• показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;

• продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;

• отвечал самостоятельно, без наводящих вопросов учителя;

• возможны одна – две неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.

Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:

• в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;

• допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;

• допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.

Отметка «3» ставится в следующих случаях:

• неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке обучающихся» в настоящей программе по математике);

• имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;

• ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;

• при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.

Отметка «2» ставится в следующих случаях:

• не раскрыто основное содержание учебного материала;

• обнаружено незнание учеником большей или наиболее важной части учебного материала;

• допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.

Отметка «1» ставится, если:

• ученик обнаружил полное незнание и непонимание изучаемого учебного материала или не смог ответить ни на один из поставленных вопросов по изученному материалу.

Общая классификация ошибок.

При оценке знаний, умений и навыков обучающихся следует учитывать все ошибки (грубые и негрубые) и недочёты.

Грубыми считаются ошибки:

• незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;

• незнание наименований единиц измерения;

• неумение выделить в ответе главное;

• неумение применять знания, алгоритмы для решения задач;

• неумение делать выводы и обобщения;

• неумение читать и строить графики;

• неумение пользоваться первоисточниками, учебником и справочниками;

• потеря корня или сохранение постороннего корня;

• отбрасывание без объяснений одного из них;

• равнозначные им ошибки;

• вычислительные ошибки, если они не являются опиской;

• логические ошибки.

К негрубым ошибкам следует отнести:

• неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;

• неточность графика;

• нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);

• нерациональные методы работы со справочной и другой литературой;

• неумение решать задачи, выполнять задания в общем виде.

Недочетами являются:

• нерациональные приемы вычислений и преобразований;

• небрежное выполнение записей, чертежей, схем, графиков.

X. Тематика контрольных работ

№ п/п Тема контрольной работы Вводный контроль №1 Натуральные числа и нуль №2 Действия с натуральными числами и свойства действий №3 Выражения №4 Делимость чисел №5 Решение текстовых задач №6 Таблицы и диаграммы №7 Обыкновенные дроби №8 Действия с обыкновенными дробями №9 Смешанные обыкновенные дроби №10 Геометрические фигуры на плоскости №11 Площади и объемы №12 Итоговая работа за 5 класс

XI. Описание учебно-методического и материально-технического обеспечения

образовательного процесса по предмету «Математика»

Для реализации целей и задач обучения математике по данной программе используется УМК по математике Образовательной системы «Школа 2100» (издательство «Баласс», www.school2100.ru).

К техническим средствам обучения, которые могут эффективно использоваться на уроках математики, относятся компьютер, цифровой микроскоп, цифровой фотоаппарат, DVD-плеер, телевизор, интерактивная доска и др.

Примеры работ при использовании компьютера:

- поиск дополнительной информации в Интернете;

– создание текста доклада;

– обработка данных проведенных математических исследований;

– создание мультимедийных презентаций (текстов с рисунками, фотографиями и т.д.), в том числе для представления результатов исследовательской и проектной деятельности.

При использовании компьютера учащиеся применяют полученные на уроках информатики инструментальные знания (например, умения работать с текстовыми, графическими редакторами и т.д.), тем самым у них формируется готовность и привычка к практическому применению новых информационных технологий. Технические средства на уроках математики широко привлекаются также при подготовке проектов (компьютер).

Обучение осуществляется по учебнику «Математика» (5 класс) в 2-х частях, авторов: С.А. Козлова, А.Г. Рубин М.: Баласс, 2011 г. (Образовательная система «Школа 2100»)

Дополнительная литература:

• Тесты для промежуточной аттестации, «Математика 5-6 классы», под редакцией Ф.Ф. Лысенко, учебно-методическое пособие, изд. «Легион», Ростов-на-Дону, 2008 г.

• Школа 2100. «Математика» 5 класс. Методические рекомендации для учителя. С.А. Козлова, А.Г. Рубин М., 2011 г.

• 20 тестов по математике ко всем учебникам по математике за 5-6 классы, С.С. Минаева, изд. «Экзамен», М., 2007 г.

• Дидактические материалы по математике для 5 класса, М., «Дрофа», 2004 г.

• Уроки математики в 5-10 классах с применением информационных технологий; методическое пособие с электронным приложением, М., изд. «Глобус», 2009 г.

• Наглядная геометрия, учебное пособие для учащихся 5-6 классов, И.Ф. Шарыгин, Л.Н. Ерганжиева, М., 1992 г.

• Математический тренажер 5 класс. Пособие для учителей и учащихся В.И. Жохов М., «Мнемозина», 2011

• Математические диктанты 5 класс. Пособие для учителя В.И. Жохов М. «Мнемозина», 2011

• Задачи на смекалку 5-6 класс И.Ф. Шарыгин, А.В. Шевкин М. «Просвещение», 2003

• Рабочая программа «Математика» 5-9 классы С.А. Козлова, А.Г. Рубин

Предполагается использование следующих программно-педагогических средств,

реализуемых с помощью компьютера:

• Математика: еженедельное учебно-методическое приложение к газете «Первое сентября». http://mat.lseptember.ru.

Для обеспечения плодотворного учебного процесса предполагается использование инфор­мации и материалов следующих интернет-ресурсов:

• Министерство образования и науки РФ: http://www.mon.gov.ru/

• Федеральное государственное учреждение «Государственный научно-исследовательский институт информационных технологий и телекоммуникаций»: http://www. informika.ru/

• Тестирование on-line: 5-11 классы: http://www.kokch.kts.ru/cdo/

• Путеводитель «В мире науки» для школьников:
  http://www.uic.ssu. samara.ru/~nauka/

• Мегаэнциклопедия Кирилла и Мефодия: http://mega.km.ru/

• Сайт энциклопедий: http://www.encyclopedia.ru/

• Электронные образовательные ресурсы к учебникам в Единой коллекции www.school-collection.edu.ru

• http://www.openclass.ru/node/226794

• http://forum.schoolpress.ru/article/44

• http://1314.ru/

• http://www.informika.ru/projects/infotech/school-collection/

• http://www.ug.ru/article/64

• http://staviro.ru

• http://www.youtube.com/watch?v=LLSKZJA8g2E&feature=related

• http://www.youtube.com/watch?v=Cn24EHYkFPc&feature=related

• http://staviro.ru/

XII. Нормативы количественной оценки учащихся

Количество часов в год	Количество оценок
170	Не менее 10- ти оценок в месяц

VIII. Тематическое планирование с определением основных видов учебной деятельности

№	Тема раздела.	дата		Содержание				Характеристика основных видов деятельности				Планируемые результаты
Тематическое планирование 5 класс
Раздел I. ЧИСЛА. Глава 1. Натуральные числа и нуль (13ч)
1.	Повторение. Действия с натуральными числами	1.09			Действия с натуральными числами, порядок их выполнения.			Уметь: - выполнять арифметические действия с натуральными числами				ЛР1, ЛР10, ЛР3, ЛР6, ПР2, ПР4, ПР6, МР1, МР2, МР14, МР21, МР26, МР23, МР33,
2.	Входной тест	2.09
3.	Плоскость, прямая, луч, отрезок	3.09			Плоскость, прямая, отрезок, луч, их обозначение			Иметь представление о плоскости. Уметь: - изображать и обозначать отрезки, прямую, лучи; - измерять их длину и строить отрезки заданной длины с помощью линейки; -описывать их взаимное расположение по готовому чертежу.
4.	Длина отрезка. Единицы измерения длины	4.09			Длина отрезка. Единицы измерения длины			Уметь: - выполнять арифметические действия с натуральными числами; - изображать отрезок, треугольник, прямоугольник с помощью линейки; - вычислять периметр треугольника и прямоугольника, площадь прямоугольника, используя формулы
5.	Анализ теста. Натуральные числа и нуль. Запись и чтение чисел	5.09			Действия с натуральными числами, порядок их выполнения, начальные сведения о геометрии			Иметь представление: - о натуральных числах; - десятичной системе счисления; - римской нумерации; - уметь читать и записывать натуральные числа
6.	Натуральные числа и нуль. Запись и чтение чисел	8.09			Натуральные числа, чтение и запись, десятичная система счисления, римская нумерация.
7.	Единичный отрезок, координаты, числовой луч	9.09			Единичный отрезок, числовой луч, координаты точки			Иметь представление об единичном отрезке. Уметь: - изображать числовой луч; - находить координаты точек, изображённых на луче; - изображать точки с заданными координатами
8.	Единичный отрезок, координаты, числовой луч	10.09
9.	Сравнение чисел	11.09			Меньше, больше, неравенство, двойное неравенство, правила сравнения натуральных чисел			Уметь сравнивать натуральные числа, записывать результат сравнения, используя, знаки сравнения
10.	Сравнение чисел	12.09
11.	Округление натуральных чисел	15.09			Округление чисел			Знать правило округления чисел. Уметь: - округлять числа; - находить приближенные значения чисел
12.	Округление натуральных чисел	16.09
13.	Контрольная работа «Натуральные числа и нуль»	17.09			Натуральные числа и нуль. Запись и чтение чисел. Единичный отрезок, координаты, числовой луч. Сравнение чисел. Округление натуральных чисел			Уметь: - читать и записывать натуральные числа; - строить отрезки и измерять их длину с помощью линейки; - строит отрезок заданной длины; - изображать прямую, луч, отрезок, учитывая их взаимное расположение; - изображать точки на числовом луче с заданными координатами; - уметь сравнивать натуральные числа - уметь округлять числа
Глава 2. Действия с натуральными числами и их свойства (32ч)
14.	Анализ контрольной работы. Сложение. Свойства сложения	18.09				Сложение натуральных чисел, свойства сложения.			Знать свойства сложения. Уметь: - выполнять сложение многозначных чисел.				ЛР2, ЛР6, ЛР9, ЛР10, МР5, МР10, МР16, МР19, МР23, МР28, МР30, МР34, МР35, ПР1, ПР2, ПР3, ПР8,
15.	Сложение. Свойства сложения	19.09
16.	Вычитание	22.09				Вычитание натуральных чисел, его свойства			Знать свойства вычитания. Уметь: - выполнять вычитание многозначных чисел
17.	Вычитание	23.09
18.	Умножение. Свойства умножения	24.09				Смысл умножения числа m на число n, компоненты действия умножения, свойства			Знать: - смысл умножения одного числа на другое; - свойства умножения. Уметь: - умножать многозначные числа; - применять свойства умножения при нахождении значения выражения
19.	Распределительное свойство	25.09				Распределительное свойство умножения			Знать распределительное свойство умножения. Уметь: - упрощать выражения, зная распределительное свойства умножения; - решать уравнения, предварительно упростив его с помощью свойств умножения
20.	Деление	26.09				Действие деления, компоненты, свойства			Знать: - смысл действия деления; - свойства деления. Уметь: - делить многозначные числа уголком; - находить неизвестные компоненты действий деления и умножения
21.	Упрощение вычислений	29.09				Распределительное свойство умножения			Уметь: - упрощать выражения, зная распределительное и сочетательное свойства умножения;
22.	Устное и письменное сложение и вычитание чисел	30.09				Сложение и вычитание чисел. Свойства.			Знать свойства сложения и вычитания. Уметь: - выполнять устно сложение и вычитание двузначные чисел; - выполнять сложение и вычитание многозначных чисел, применяя свойства
23.	Устное и письменное сложение и вычитание чисел	1.10
24.	Устное и письменное умножение чисел	2.10				Умножение чисел. Свойства			Знать свойства умножения Уметь: - выполнять умножение многозначных чисел, применяя свойства
25.	Устное и письменное умножение чисел	3.10
26.	Степень числа. Квадрат и куб числа	6.10				Степень числа, основание степени, показатель степени			Уметь: - представлять произведение числа в виде степени и наоборот; - находить значение квадрата и куба числа
27.	Степень числа. Квадрат и куб числа	7.10
28.	Деление с остатком	8.10				Компоненты действия деления с остатком			Знать компоненты действия деления с остатком. Уметь: - выполнять деление с остатком; - находить делимое по неполному частному, делителю и остатку
29.	Устное и письменное деление чисел	9.10				Деление чисел. Свойства			Знать свойства деления. Уметь: - выполнять деление чисел, применяя свойства
30.	Устное и письменное деление чисел	10.10
31.	Контрольная работа «Действия с натуральными числами и их свойства»	13.10				Сложение. Свойства сложения. Вычитание. Умножение. Свойства умножения. Распределительное свойство. Деление. Степень числа. Квадрат и куб числа. Деление с остатком			Уметь: - выполнять сложение, вычитание, умножение, деление многозначных чисел, применяя свойства; -представлять произведение числа в виде степени и наоборот; - находить значение квадрата и куба числа - выполнять деление с остатком; - находить делимое по неполному частному, делителю и остатку
32.	Анализ контрольной работы	14.10							Анализировать работу, находить и исправлять ошибки				ЛР1, ЛР3, ЛР9, ЛР10, МР2, МР5, МР7, МР10, МР13, МР14, МР17, МР18, МР23, МР28, МР31, МР34, МР36, ПР3, ПР7,
33.	Выражения. Порядок действий в выражениях	15.10				Выражения. Порядок действий в выражениях			Знать порядок действия в выражениях Уметь: - определять порядок действий в выражении; - находить значение выражения
34.	Буквенные выражения	16.10				Буквенные выражения, значение выражения			Иметь представление о буквенных выражениях. Уметь: - составлять буквенные выражения по условиям задач; - осуществлять в буквенных выражениях числовые подстановки; - вычислять значения буквенных выражений, зная значение буквы
35.	Уравнение	17.10				Уравнение, корень уравнения					Уметь: - проверять, является ли данное число корнем уравнения; - решать уравнения, зная правило нахождения компонентов действий сложения и вычитания
36.	Уравнение	20.10 21.10
37.	Уравнение
38.	Задачи на части	22.10 23.10				Часть. Задачи на части. Метод их решения			Уметь: -решать задачи на части с помощью схем
39.	Задачи на части
40.	Нахождение двух чисел по их сумме и разности	24.10				Сумма и разность чисел.			Знать сумму и разность чисел. Уметь: - находить два числа по их сумме и разности
41.	Перебор возможных вариантов	27.10				Число вариантов. Дерево выбор. Число всех возможных пар			Знать число вариантов, дерево выбора, число всех возможных пар. Уметь: - решать задачи с помощью дерева выбора -находить число всех возможных пар
42.	Занимательные задачи	28.10				Логическая задача. Таблица истинности. Граф			Знать метод составления таблицы истинности, граф. Уметь: - решать логические задачи с помощью таблицы истинности и графов.
43.	Контрольная работа «Буквенные выражения»»	29.10				Порядок действий в выражениях. Буквенные выражения. Уравнение. Задачи на части			Уметь: - осуществлять в буквенных выражениях числовые подстановки; - вычислять значения буквенных выражений, зная значение буквы; - находить значение выражения, определяя порядок
44.	Итоговый тест за 1 четверть	30.10
45.	Анализ теста и контрольной работы	31.10
Раздел II. Делимость Глава 3. Делимость чисел (28ч)																	Раздел II. Делимость Глава 3. Делимость чисел (28ч)
46.	Входной тест	10.11				Делители, кратные, делители, кратные свойства делимости			Уметь формулировать определения делителя, кратного. Свойства делимости Уметь находить делители и кратные данных натуральных чисел; применять свойства делимости при решении текстовых задач
	Делимость. Свойства делимости
47.	Признаки делимости	11.11				Признаки делимости на 10, на 5, на 2. Четные и нечетные числа. Признаки делимости на 9 и на 3. Признаки делимости на 10, на 5, на 2. Четные и нечетные числа Признаки делимости на 9 и на 3.			Знать признаки делимости на 10, на 5 и на 2. Уметь распознавать числа, кратные 10, 5 и 2. Знать признаки делимости на 9 и на 3. Уметь распознавать числа, кратные 9 и 3. Уметь распознавать числа, кратные 10, 5,2, 9 и 3.				ПР4, ПР5, МР6, МР10, МР12, МР17, МР15, МР19, МР20, МР23, МР32, Мр33, Мр36, ЛР11, ЛР6, ЛР3
48.	Признаки делимости	12.11
49.	Признаки делимости	13.11
50.	Простые и составные числа	14.11				Простые натуральные числа. Составные натуральные числа. Разложение натуральных числе на множители.			Знать определение простого и составного числа. Распознавать простые и составные числа. Распознавать простые и составные числа. Уметь раскладывать составные числа на множители.
51.	Делители и кратные	17.11				Делитель, кратное, наименьшее кратное натурального числа			Знать определения делителя и кратного Уметь находить делители и кратные данных натуральных чисел.
52.	Делители и кратные	18.11
53.	Наибольший общий делитель	19.11				Наибольший об­щий делитель двух натураль­ных чисел. Вза­имно простые числа. Разложение на простые множители. Алгоритм нахождения НОД НОД натураль­ных чисел, вза­имно простые числа, алгоритм нахождения НОД			Знать определения НОД, взаимно простых чисел, разложение на простые множители, алгоритм нахож­дения НОД. Уметь находить НОД для двух и более натуральных чисел Уметь находить НОД чисел, оп­ределять пары взаимно простых чисел, раскладывать составные числа на простые множители
54.	Наибольший общий делитель	20.11
55.	Нахождение НОД чисел	21.11
56.	Наименьшее общее кратное	24.11				Наименьшее об­щее кратное двух натуральных чи­сел. Алгоритм нахождения НОК Признаки дели­мости, простые и составные чис­ла, НОК И НОД натуральных чи­сел			Знать, какое число называют НОК чисел, алгоритм нахождения НОК чисел. Уметь находить НОК двух и более натуральных чисел Уметь, используя признаки дели­мости натуральных чисел, нахо­дить НОК и НОД натуральных чи­сел, распознавать взаимно простые числа
57.	Нахождение НОК чисел	25.11
58.	НОД и НОК	26.11
59.	Обобщающее повторение по теме.	27.11				Признаки дели­мости, простые и составные чис­ла, НОК И НОД натуральных чи­сел, взаимно про­стые числа			Уметь раскладывать числа на про­стые множители; находить НОК и НОД натуральных чисел; распо­знавать взаимно простые числа
60.	Контрольная работа «Делимость чисел»	28.11							Анализировать работу, находить и исправлять ошибки
61.	Анализ контрольной работы Единицы измерения времени	1.12				Единицы измерения времени			Знать единицы измерения времени. Уметь: -выражать одни единицы измерения величины в другие - решать текстовые задачи с использованием единиц измерения времени				ПР5, ПР2, ПР1, Мр35, МР34, МР32, МР30, МР21, МР19, Мр15, МР6, МР2, МР10, ЛР9, ЛР3
62.	Единицы измерения времени	2.12				Скорость движения, время, путь. Виды задач на движение: - движение одного объекта - в одном направлении - в противоположном направлении - навстречу - вдогонку - движение по реке			Знать определение скорости движения, времени, пути. Выполнять вычисления по формулам. Уметь: - использовать знания о зависимостях между величинами (скорость, время, расстояние) -решать задачи на движение нескольких типов: движение одного объекта, в одном направлении, в противоположном направлении, навстречу, вдогонку, движение по реке -осмыслять текст задачи, извлекать необходимую информацию.
63.	Задачи на движение	3.12
64.	Движение навстречу друг другу	4.12
65.	Движение в противоположных направлениях	5.12
66.	Движение вдогонку	8.12				Угол, элементы угла, обозначение угла, развернутый угол, прямой угол Транспортир, градус, острый угол, тупой угол, перпендикулярные прямые			Иметь представление об углах. Уметь: -изображать и обозначать угол; - сравнивать их; -изображать и распознавать прямой углы с помощью транспортира. Знать определение острого и прямого углов. Иметь представление о перпендикулярных прямых Уметь: -распознавать острые и тупые углы с помощью транспортира; -изображать углы заданной величины с помощью транспортира; -измерять углы с помощью транспортира.
67.	Движение по воде	9.12
68.	Движение по воде	10.12				Ломанная линия, ее элементы. Многоугольник, его элементы. Периметр многоугольника			Знать определение ломанной линии и ее элементов, многоугольника и его элементов. Уметь: -распознавать многоугольники и его элементы -строить диагональ многоугольника -находить периметр многоугольника
69.	Угол	11.12
70. 71. 72.	Решение задач на движение. Угол. Ломаные и многоугольники. Ломаные и многоугольники	12.12 15.12 16.12				Единицы измерения времени. Задачи на движение. Углы. Измерение углов. Многоугольники			Уметь: -решать текстовые задачи с использованием единиц измерения времени - решать задачи на движение нескольких типов: движение одного объекта, в одном направлении, в противоположном направлении, навстречу, вдогонку, движение по реке - изображать углы заданной величины с помощью транспортира; -измерять углы с помощью транспортира - распознавать многоугольники и его элементы - находить периметр многоугольника
73	Контрольная работа «Задачи на движение. Многоугольники»						17.12			Анализировать работу, находить и исправлять ошибки
Глава 4. Таблицы и диаграммы (7 ч)
74.	Чтение и составление таблиц	18.12				Таблица, ее элементы Балансовая таблица. Линейная диаграмма. Столбчатая диаграмма.			Иметь представление о таблицах и их элементах. Уметь: - читать таблицы -строить таблицы по условиям текстовых задач. Иметь представление о линейных и столбчатых диаграммах. Уметь строить линейные и столбчатые диаграммы по условиям текстовых задач.				ЛР3, ЛР6, ЛР10, МР5,МР13, МР18, МР21, МР32, МР34, МР35, ПР1, ПР6, ПР10
75	Чтение и составление линейных и столбчатых диаграмм	19.12
76	Чтение и составление линейных и столбчатых диаграмм	22.12
77	Опрос общественного мнения	23.12				Таблица истинности.			Уметь решать текстовые задачи с помощью таблиц, линейных и столбчатых диаграмм.
78	Опрос общественного мнения	24.12
79.	Итоговый тест за 2 четверть	25.12
80.	Анализ работы	26.12
Глава 5. Дроби (13ч)
81.	Входной тест Понятие дроби	12.01				- находить половину, треть и четверть; - изображать обыкновенные дроби на числовом луче; - понятие обыкновенная дробь, числитель, знаменатель.					Иметь представление об обыкновенных дробях, числителе, знаменателе дроби; Уметь: -читать и записывать		ПР2, ПР1, МР35, МР32, МР31, МР19, МР14, МР8, МР6, МР2, МР1, ЛР1, ЛР3, ЛР7
82.	Понятие дроби	13.01				Доли, обыкновенная дробь, числитель, знаменатель			Иметь представления об обыкновенных дробях. Понимать, что показывают числитель и знаменатель.
83.	Нахождение части от целого и целого по его части	14.01				часть от числа и числа по его дроби			Уметь: - читать и записывать обыкновенную дробь; - находить значение дроби от числа и число по значению его дроби
84.	Нахождение части от целого и целого по его части	15.01
85	Натуральные числа и дроби	16.01				Натуральное число. Дробь			Уметь представлять натуральное число в виде дробного числа
86.	Натуральные числа и дроби	19.01
87	Основное свойство дроби. Приведение дробей к общему знаменателю	20.01				Основное свойство дроби. Сокращение дроби. Несократимая дробь. Общий знаменатель. Дополнительный множитель			Знать основное свойство дроби, правило сокращение дробей, приведение к общему знаменателю. Уметь - записывать с помощью букв основное свойство дроби -применять основное свойство дроби -сокращать дроби -находить дополнительный множитель и приводить дроби к общему знаменателю.
88.	Основное свойство дроби. Приведение дробей к общему знаменателю	21.01
89.	Основное свойство дроби. Приведение дробей к общему знаменателю	22.01
90.	Сравнение дробей	23.01
91.	Сравнение дробей	26.01				Сравнение дробей с одинаковыми и разными знаменателями			Знать правило сравнения дробей с одинаковыми и разными знаменателями Уметь сравнивать дроби с одинаковыми и разными знаменателями
92.	Обобщающее повторение по теме	27.01
93.	Контрольная работа «Основное свойство дроби. Сравнение дробей»	28.01				Понятие дроби. Нахождение части от целого и целого по его части. Натуральные числа и дроби. Основное свойство дроби. Приведение дробей к общему знаменателю. Сравнение дробей.			Уметь: - изображать обыкновенные дроби на числовом луче; - сравнивать дроби; - находить дробь от числа; - находить число по значению его дроби; -сокращать дроби -находить дополнительный множитель и приводить дроби к общему знаменателю.
94.	Анализ контрольной работы	29.01							Анализировать работу, находить и исправлять ошибки
Глава 6. Действия с дробями (36 ч)
95.	Сложение дробей. Свойства сложения	30.01				Сложение с одинаковыми и разными знаменателями. Свойства сложения.			Знать правила сложения дробей с одинаковыми и разными знаменателями; Уметь -выполнять действие сложения дробей с одинаковыми и разными знаменателями; -решать задачи на применение сложения дробей				ЛР3, ЛР6, ЛР9, МР1, МР3, МР6, МР13, МР17, МР19, МР30, МР34, МР36, ПР4, ПР8
96.	Сложение дробей. Свойства сложения	2.02
97.	Сложение дробей. Свойства сложения	3.02
98.	Вычитание дробей	4.02				Вычитание с одинаковыми и разными знаменателями.			Знать правила вычитания дробей с одинаковыми и разными знаменателями. Уметь - выполнять действие вычитания дробей с одинаковыми и разными знаменателями; -уметь решать задачи на применение вычитания дробей
99.	Вычитание дробей	5.02
100	Вычитание дробей	6.02
101	Умножение дробей. Свойства умножения	9.02				Умножение дробей. Свойства умножения			Знать правила умножения дробей. Уметь: -выполнять действие умножения дробей на натуральное число; -уметь решать задачи, применяя умножение дробей. Знать свойства умножения дробей. Уметь применять данные свойства
102	Умножение дробей. Свойства умножения	10.02
103	Умножение дробей. Свойства умножения	11.02
104	Деление дробей	12.02				Деление дробей. Обратная дробь.			Знать правила деления дробей Уметь -выполнять действие деления дробей на натуральное число; -находить дроби обратные данным; -уметь решать задачи, применяя умножение и деление дробей на натуральное число.
105	Деление дробей	13.02
106	Деление дробей	16.02
107	Задачи на совместную работу	17.02				Задачи на совместную работу			Знать алгоритм решения задач на совместную работу. Уметь решать задачи на совместную работу
108	Задачи на совместную работу	18.02
109	Задачи на совместную работу	19.02
110	Задачи на совместную работу	20.02
111	Контрольная работа «Умножение и деление дробей»	23.02				Сложение дробей. Свойства сложения. Вычитание дробей. Умножение дробей. Свойства умножения. Деление дробей. Задачи на совместную работу			Уметь: - выполнять вычисления с обыкновенными дробями; -решать текстовые задачи с использованием дробей - анализировать и осмысливать текст задачи, переформулировать условие, извлекать необходимую информацию, критически оценивать ответ.
112	Анализ контрольной работа	24.02							Анализировать работу, находить и исправлять ошибки				ЛР3, ЛР6, ЛР9, МР1, МР3, МР6, МР13, МР17, МР19, МР30, МР34, МР36, ПР4, ПР8
113	Понятие смешанной дроби	25.02				Правильная и неправильная дробь. Смешанное число, целая и дробная часть числа. Сравнение смешанных дробей.			Иметь представление о смешанных числах. Уметь: -читать и записывать смешанные числа; -уметь выделять целую часть из неправильной дроби -представлять смешанное число в виде неправильной дроби; -сравнивать смешанные дроби.
114	Понятие смешанной дроби	26.02
115	Сложение и вычитание смешанных дробей	27.02				Правила сложения и вычитания смешанных дробей			Знать правила сложения и вычитание смешанных дробей. Уметь - выполнять действие сложения и вычитания смешанных чисел; - уметь решать задачи, применяя данные действия смешанных дробей.
116	Сложение и вычитание смешанных дробей	2.03
117	Сложение и вычитание смешанных дробей	3.03
118	Сложение и вычитание смешанных дробей	4.03
119	Умножение и деление смешанных дробей	5.03				Правила умножения и деления смешанных дробей			Знать правила умножения и деления дробей; Уметь: - выполнять действие умножения и деления смешанные дроби; -решать задачи, применяя данные действия смешанных дробей.
120	Умножение и деление смешанных дробей	6.03
121	Умножение и деление смешанных дробей	9.03
122	Умножение и деление смешанных дробей	10.03
123	Занимательные задачи	11.03				Занимательные задачи			Уметь решать занимательные задачи методом «самый неудобный случай»
124	Занимательные задачи	12.03
125	Занимательные задачи	13.03
126	Обобщающее повторение по теме «Умножение и деление дробей»	16.03				Понятие смешанной дроби. Сложение и вычитание смешанных дробей. Умножение и деление смешанных дробей			Уметь: - выделять целую часть из неправильной дроби - представлять смешанное число в виде неправильной дроби; - сравнивать смешанные дроби; - выполнять вычисления со смешанными дробями; -решать текстовые задачи с использованием данных дробей - анализировать и осмысливать текст задачи, переформулировать условие, извлекать необходимую информацию, критически оценивать ответ.
127	Контрольная работа «Умножение и деление дробей» 17.03									Анализировать работу, находить и исправлять ошибки
128	Итоговый тест 18.03
129	Анализ контрольной работы и теста 19.03
130	Решение занимательных задач 20. 03
Раздел IV. Геометрические фигуры Глава 7. Геометрические фигуры на плоскости (12 ч)
131	Входной тест. Треугольники и их виды		1.04				Треугольник, его элементы. Виды треугольника.			Знать какая фигура называется треугольником, его элементы. Уметь: - строить треугольники; - определять виды треугольников				ПР8, ПР2, ПР1, МР30, МР31, МР32, МР25, МР10, МР17, ЛР10, ЛР8, ЛР3, ЛР2
132	Треугольники и их виды		2.04
133	Равенство геометрических фигур		3.04				Равенство фигур. Признаки равенства.			Знать какие фигуры называются равными. Уметь: - определять равные фигуры; -применять признаки равенства.
134	Равенство геометрических фигур		6.04
135	Окружность и круг		7.04				Окружность и ее элементы. Круг.			Знать отличие окружности от круга. Уметь: -изображать окружность и ее элементы
136	Окружность и круг		8.04
137	Центральные углы и дуги		9.04				Центральный угол. Дуги. Фигуры и их границы. Плоские углы.			Знать определение центрального угла. Уметь: - определять, чему равен центральный угол, опирающийся на часть окружности; -определять на какую часть окружности опирается центральный угол; -строить углы заданной величины.
138	Центральные углы и дуги		10.04
139	Круговые диаграммы		13.04				Круговые диаграммы			Иметь представление о круговых диаграммах. Уметь - строить круговые диаграммы; - решать текстовые задачи, применяя круговые диаграммы.
140	Круговые диаграммы		14.04
141	Контрольная работа «Геометрические фигуры»		15.04				Треугольники и их виды. Окружность и круг. Центральные углы и дуги. Круговые диаграммы			Уметь: - распознавать геометрические фигуры на чертежах, рисунках - изображать геометрические фигуры и их конфигурации с помощью чертежных инструментов -изображать и находить равные фигуры -исследовать и описывать свойства геометрических фигур
142	Анализ контрольной работы 16.04									Анализировать работу, находить и исправлять ошибки
Глава 8. Площади и объёмы (16 ч)
143	Единицы измерения площадей. Площадь прямоугольника. Площадь прямоугольного треугольника	17.04				Единицы измерения площадей. Площадь квадрата. Площадь прямоугольника. Высота треугольника. Площадь прямоугольного треугольника. Площадь треугольника.			Знать единицы измерения площадей. Площадь квадрата. Площадь прямоугольника. Иметь представление о площади фигур. Уметь: - выражать одни единицы измерения в другие; - вычислять площадь квадрата и площадь прямоугольника; Уметь: - строить высоту треугольника; - вычислять площадь прямоугольного треугольника и площадь треугольника.				ПР(, ПР5, ПР6, ПР7, ПР1, ПР2, МР31, МР22, МР20, МР17, МР11, МР7, МР3, ЛР9, ЛР1, ЛР3
144	Единицы измерения площадей. Площадь прямоугольника. Площадь прямоугольного треугольника	20.04
145	Единицы измерения площадей. Площадь прямоугольника. Площадь прямоугольного треугольника	21.04
146	Геометрические фигуры в пространстве	22.04				Геометрические фигуры в пространстве, их виды и элементы			Иметь представление о геометрических фигурах в пространстве. Уметь: - определять виды геометрических фигур и их элементы - изображать геометрические фигуры в пространстве
147	Геометрические фигуры в пространстве	23.04
148	Объём параллелепипеда. Единицы измерения объёма	24.04				Объём параллелепипеда. Объем куба. Единицы измерения объёма.			Знать единицы измерения объёма, объём параллелепипеда, объем куба. Иметь представление о площади фигур. Уметь: - выражать одни единицы измерения объема в другие; - вычислять объём параллелепипеда, объем куба.
149	Объём параллелепипеда. Единицы измерения объёма	27.04
150	Объём параллелепипеда. Единицы измерения объёма	28.04
151	Понятие о вероятности	29.04				Случайный эксперимент. Событие. Вероятность событий. Вероятности невозможного и достоверного событий.			Иметь представление о вероятности. Уметь: - выписывать множество всевозможных результатов (сходов) простейших случайных экспериментов; - находить вероятности простейших случайных событий.
152	Понятие о вероятности	30.04
153	Понятие о вероятности	4.05
154	Занимательные задачи	5.05				Математическая игра			Уметь решать математические игры.
155	Занимательные задачи	6.05
156	Занимательные задачи	7.05
157	Контрольная работа «Площади и объемы»	8.05				Единицы измерения площадей. Площадь прямоугольника. Площадь прямоугольного треугольника. Геометрические фигуры в пространстве. Объём параллелепипеда. Единицы измерения объёма. Понятие о вероятности.			Уметь: - выражать одни единицы измерения в другие; - вычислять площадь квадрата и площадь прямоугольника, используя формулу площади квадрата и прямоугольника; - вычислять площадь прямоугольного треугольника и площадь треугольника, используя формулу площади; - определять виды геометрических фигур и их элементы; - вычислять объём параллелепипеда, объем куба, используя формулу; - выписывать множество всевозможных результатов (сходов) простейших случайных экспериментов; - находить вероятности простейших случайных событий.
158	Анализ контрольной работы 11.05									Анализировать работу, находить и исправлять ошибки
Итоговое повторение курса математики 5 класса (13ч)
159	Арифметические действия с натуральными и дробными числами.	12.05				Понятие натурального числа, обыкновенной дроби, десятичной дроби, арифметические действия с указанными числами, свойства действий			Иметь представление о натуральных числах, об обыкновенных и десятичных дробях. Знать свойства арифметических действий. Уметь выполнять арифметические действия с указанными числами				ЛР1, ЛР3, ЛР7, МР6, МР15, МР»!, МР23, МР30, МР32, МР31, МР33, МР36, ПР3, ПР8, ПР10
160	Арифметические действия с натуральными и дробными числами.	13.05
161	Арифметические действия с натуральными и дробными числами.	14.05
162	Буквенные выражения, упрощение выражений, формулы.	15.05				Буквенные выражения, формулы: пути, площади и периметра прямоугольника, объёма прямоугольного параллелепипеда			Уметь составлять буквенные выражения по условию задачи, упрощать и находить их значение. Знать - формулы пути, площади и периметра прямоугольника; - объёма прямоугольного параллелепипеда. Уметь применять указанные формулы при решении текстовых задач
163	Буквенные выражения, упрощение выражений, формулы.	18.05
164	Уравнения, решение задач с помощью уравнений.	19.05				Уравнение, корень уравнения, компоненты арифметических действий			Знать определения уравнения, корня уравнения. Уметь решать уравнения, используя компоненты арифметических действий. Уметь решать задачи с помощью уравнений
165	Уравнения, решение задач с помощью уравнений.	20.05
166	Делимость чисел. НОД и НО К	21.05				Уравнение, корень уравнения, компоненты арифметических действий					Знать признаки делимости на 10, на 5 и на 2, на 9 и на 3; Формулировать определение простого и составного числа; делителя и кратного; определения НОД и НОК, взаимно простых чисел, разложение на простые множители, алгоритм нахож­дения НОД и НОК. Уметь: - распознавать числа, кратные 10, 5,2, 9 и 3; - раскладывать числа на про­стые множители; - находить НОК и НОД натуральных чисел; - распо­знавать взаимно простые числа
167	Делимость чисел	22.05
168	Дроби и действия с ними.	25.05				Основное свой­ство дроби. Сокращение дро­бей. Сравнение, сложение, вычи­тание, умножение, деление дробей и смешанных чисел.					Знать основное свойство дроби, определение сокращения дроби, определения дополнитель­ного множителя. Уметь: - приводить дроби к общему знаменателю; -сокращать дроби; - сравни­вать; - выполнять вычисления с дробями;
169	Итоговая контрольная работа	26.05				Натуральные числа и нуль. Действия с натуральными числами. Делимость натуральных чисел. Таблицы и диаграммы. Дроби. Действия с дробями. Геометрические фигуры. Площади и объемы.					Уметь: -выполнять действия с натуральными числами; - выполнять действия обыкновенными дробями; -выполнять умножение и деление с 1000; -вычислять значения выражений, содержащих 3-4 действия со скобками и без них; -раскладывать натуральное число на множители; -находить наибольший общий делитель и наименьшее общее кратное нескольких чисел; -решать простые и составные текстовые задачи; -решать удобным для себя способом (в том числе и с помощью таблиц и графов) комбинированные задачи; -решать удобным для себя способом (в том числе и с помощью графов и таблиц) логические задачи; - находить вероятности простейших случайных событий.
169	Анализ контроль ной рабо­ты	27.05									Анализировать работу, находить и исправлять ошибки
170	Итоговый урок	28.05

IX. Тематическое планирование с определением основных видов учебной деятельности

№ п\п	Тема раздела				Дата		Дата		Содержание	Характеристика основных видов деятельности		Планируемые результаты
Тематическое планирование 6 класс
Раздел I. Десятичные дроби (45 ч) Глава 1. Повторение. Обыкновенные дроби (10 ч)
1.	Входной тест				1.09
2.	Обыкновенные дроби. Основное свойство дроби.				2.09				Нахождение части от целого и целого по его части. Натуральные числа и дроби. Основное свойство дроби. Приведение дробей к общему знаменателю. Понятие неправильной и смешанной дроби. Преобразование неправильной дроби в смешанную и наоборот. Сравнение дробей. Сложение дробей. Свойства сложения. Вычитание дробей. Умножение дробей. Свойства умножения. Деление дробей. Используют разные приемы проверки правильности ответа	Знать основное свойство дроби, правило сокращение дробей, приведение к общему знаменателю. Уметь - записывать с помощью букв основное свойство дроби -применять основное свойство дроби -сокращать дроби -находить дополнительный множитель и приводить дроби к общему знаменателю. Знать правила умножения дробей. Уметь: -выполнять действие умножения дробей на натуральное число; -уметь решать задачи, применяя умножение дробей. Знать свойства умножения дробей. Уметь применять данные свойства Знать правила деления дробей Уметь -выполнять действие деления дробей на натуральное число; -находить дроби обратные данным; -уметь решать задачи, применяя умножение и деление дробей на натуральное число.		Л1, Л2, Л6, Л9, Л11, М1, М2, М5, М19, М32, П1, П2, П3, П7,
3.	Приведение дробей к общему знаменателю.				3.09
4.	Преобразование и сравнение дробей				4.09
5.	Сложение и вычитание дробей				5.09
6.	Умножение и деление дробей				8.09
7.	Решение задач на преобразование и сравнение дробей				9.09
8.	Решение задач на сложение и вычитание дробей				10.09
9.	Решение задач на умножение и деление дробей				11.09
10.	Контрольная работа №1 «Обыкновенные дроби»				12.09
Глава 2. Десятичные дроби (23 часа)
11.	Анализ контрольной работы. Понятие десятичной дроби.		15.09						Понятие десятичной дроби. Разряды десятичных дробей. Изображение десятичных дробей на числовом луче. Метрическая система мер. Сравнение дробей. Сложение дробей. Свойства сложения. Вычитание дробей. Умножение дробей. Свойства умножения. Деление дробей. Деление и умножение десятичной дроби на 10, 100, 1000… Умножение и деление десятичных дробей на натуральное число. Округление чисел до определенного разряда. Условие, при котором возможно преобразование обыкновенной дроби в десятичную; способы преобразования обыкновенных дробей в десятичные.	Знать правила ко­роткой записи десятич­ной дроби; чтение и за­пись десятичных дробей; Уметь изображать десятичные дроби на числовом луче. Знать правило срав­нения десятичных дро­бей; запись десятичной дроби с пятью (и более) знаками после запятой, равной данной. Уметь выполнять сло­жение и вычитание деся­тичных дробей. Знать, что по­казывает каждая цифра после запятой. Уметь решать задачи на сложение и вычитание десятичных дробей Знать правила умножения десятичной дроби на натуральное число. Уметь за­писывать произведения в виде суммы; запись суммы в виде произведе­ния. Уметь преобразовывать обыкновенные дроби в десятичные. Знать правило ок­ругления чисел. Уметь записывать натуральные числа, ме­жду которыми располо­жены десятичные дроби. Вывести правило деления десятич­ной дроби на натураль­ное число, на 10, 100, 1000… Деление десятич­ных дробей на натураль­ные числа; запись обык­новенной дроби в виде десятичной; решение задач по теме деления десятичных дробей на натуральные числа.		Л11, Л7, Л3, Л2, Л1, М5, М8, М15, М30, П4, П9
12.	Запись и чтение десятичных дробей		16.09
13.	Десятичные дроби и метрическая система мер		17.09
14.	Сравнение десятичных дробей		18.09
15.	Сложение и вычитание десятичных дробей		19.09
16.	Задачи на сложение и вычитание десятичных дробей		22.09
17.	Деление и умножение десятичной дроби на 10, 100 и т.д.		23.09
18.	Умножение десятичной дроби на натуральное число		24.09
19.	Умножение десятичных дробей		25.09
20.	Умножение десятичных дробей		26.09
21.	Деление десятичной дроби на натуральное число		29.09
22.	Деление десятичных дробей		30.09
23.	Деление десятичных дробей		1.10
24.	Вычисления с десятичными дробями		2.10
25.	Вычисления с десятичными дробями		3.10
26.	Приближение десятичных дробей		6.10
27.	Приближение десятичных дробей		7.10
28.	Приближенные вычисления с десятичными дробями		8.10
29.	Приближенные вычисления с десятичными дробями		9.10
30.	Преобразование обыкновенных дробей в десятичные		10.10
31.	Преобразование обыкновенных дробей в десятичные		13.10
32.	Обобщающее повторение по теме «Десятичные дроби»		14.10
33.	Контрольная работа №2 «Десятичные дроби»		15.10						Используют разные приемы проверки правильности ответа
Глава 3. Элементы геометрии (12ч)
34.	Анализ контрольной работы. Смежные и вертикальные углы		16.10						Смежные и вертикальные углы. Решение задач с использованием свойств этих углов Перпендикулярные прямые, построение и определение перпендикулярных прямых на чертеже Параллельные прямые, построение и определение параллельных прямых на чертеже. Расстояние между параллельными прямыми. Параллелограмм; виды параллелограммов; высота, площадь параллелограмма. Симметрия; центрально-симметричные фигуры.	Знать: определения и свойства смежных и вертикальных углов, определения перпендикулярных, параллельных и скрещивающихся прямых, что такое расстояние, как измеряется расстояние между точками, от точки до прямой, Уметь: выполнять чертежи смежных и вертикальных углов, узнавать смежные и вертикальные углы на составном чертеже; определять и строить на чертеже перпендикулярные, параллельные и скрещивающиеся прямые; находить расстояние от точки до прямой и между двумя параллельными прямыми		Л4, Л8, Л10, М7, М21, М25, М32, П2, П9
35.	Решение задач по теме «Смежные и вертикальные углы»		17.10
36.	Параллельные прямые		20.10
37.	Параллельные прямые		21.10
38.	Параллелограмм		22.10
39.	Параллелограмм		23.10
40.	Решение задач по теме «Параллелограмм»		24.10
41.	Центральная симметрия		27.10
42.	Центральная симметрия		28.10
43.	Обобщающее повторение по теме «Элементы геометрии»		29.10
44.	Контрольная работа № 3 «Элементы геометрии»		30.10
45.	Итоговый тест за 1 четверть		31.10						Используют разные приемы проверки правильности ответа
Раздел II. Пропорции и проценты (35 ч) Глава IV. Пропорции (21 ч)
46.	Входной тест		10.11
47.	Отношение чисел и величин		11.11						Понятие пропорции, крайних и средних членов пропорции, основное свойство пропорции. Задачи на отношения как задачи на части. Отношение двух чисел, сравнение чисел, равенства двух отношений, пропорция. Отношение чисел, величин. Прямая и обратная пропорциональность. Масштаб. Подобие, подобные фигуры.	Иметь представление о пропорциональных величинах, о прямо пропорциональных величинах, об обратно пропорциональных величинах. Уметь воспроизводить правила и примеры, работать по заданному алгоритму. Иметь представление о пропорции, о верной пропорции, об основном свойстве пропорции, о решении задач на пропорцию. Уметь воспроизводить изученную информацию с заданной степенью свёрнутости, подбирая аргументы, соответствующие решению, правильно оформлять работу. Знать понятия пропорциональных величин и масштаба. Подобие фигур. Уметь: пользоваться масштабом при работе с картой, планом дома; воспроизводить прочитанную информацию с заданной степенью свёрнутости. Правильно оформлять решения, выбрать из данной информации нужную.		Л11, Л6, Л3, М14, М18, М25, М32, П1, П2, П9
48.	Отношение чисел и величин		12.11
49.	Отношение чисел и величин		13.11
50.	Деление чисел в данном отношении		14.11
51.	Деление чисел в данном отношении		17.11
52.	Деление чисел в данном отношении		18.11
53.	Пропорции		19.11
54.	Пропорции		20.11
55.	Прямая пропорциональная зависимость		21.11
56.	Обратная пропорциональная зависимость		24.11
57.	Задачи на прямую и обратную пропорциональность		25.11
58.	Задачи на прямую и обратную пропорциональность		26.11
59.	Решение задач на пропорции		27.11
60.	Решение задач на пропорции		28.11
61.	Решение задач на пропорции		1.12
62.	Масштаб		2.12
63.	Масштаб		3.12
64.	Пропорциональность в геометрии		4.12
65.	Подобные фигуры		5.12
66.	Контрольная работа № 4. «Пропорции»		8.12						Используют разные приемы проверки правильности ответа
Глава V. Проценты (14 ч)
67.		Анализ контрольной работы. Понятие о процентах		9.12					Понятие процен­та; обращение дроби в проценты и наоборот; запись числа в процентах. Процент от числа и число по его процентам. Уменьшение или увеличение числа на процент. Способы решения задач на проценты.		Знать понятие процента. Уметь решать простейшие задачи на проценты; находить число по его процентам и процентов по его числу. Уметь решать задачи на уменьшение и увеличение числа на данное число процентов.		Л1, Л2, Л11, М1, М2, М5, М16, М26, М32, М35, П4, П8
68.		Простейшие задачи на проценты		10.12
69.		Нахождение процентов от числа		11.12
70.		Нахождение числа по его процентам		12.12
71.		Процентное отношение двух чисел		15.12
72.		Увеличение числа на данное число процентов		16.12
73.		Уменьшение числа на данное число процентов		17.12
74.		Уменьшение и увеличение чисел на число процентов		18.12
75.		Решение задач		19.12
76.		Решение задач		22.12
77.		Решение задач		23.12
78.		Решение простейших задач из ГИА на проценты		24.12
79.		Контрольная работа №5 «Проценты»		25.12					Используют разные приемы проверки правильности ответа
80.		Итоговый тест за 2 четверть		26.12
Раздел III. Положительные и отрицательные числа (51 ч) Глава VI. Целые числа (23 ч)
81.		Входной тест		12.01
82.		Целые отрицательные числа		13.01					Понятия: целое число, модуль целого числа, положительные и отрицательные числа. Сравнение целых чисел. Правила сложения, вычитания, умножения и деления целых чисел.		Иметь представление о положительных и отрицательных числах, о координатной прямой. Уметь: воспроизводить прослушанную и прочитанную информацию с заданной степенью свёрнутости; подбирать аргументы для решения, участвовать в диалоге. Уметь: показывать числа разного знака на числовой прямой, сравнивать положительные и отрицательные числа с нулём; формировать умение работать по заданному алгоритму, доказывать правильность решения с помощью аргументов; давать оценку информации, фактам, процессам, определять их актуальность. Уметь: выполнять вычисления значений выражений, в которых рассматриваются суммы положительных и отрицательных чисел; воспринимать устную речь, участвовать в диалоге, аргументировано отвечать, приводить примеры; излагать информацию, обосновывая свой собственный подход. Знать правило умножения отрицательных чисел, распределительного закона относительно вычитания. Знать правило деления отрицательных чисел. Уметь воспринимать устную речь участвовать в диалоге, понимать точку зрения собеседника, подбирать аргументы для ответа на поставленный вопрос. Приводить примеры		Л6, Л11, М2, М3, М6, М10, М19, М28, М36, П3, П4,
83.		Целые отрицательные числа		14.01
84.		Модуль целого числа		15.01
85.		Модуль целого числа		16.01
86.		Сравнение целых чисел		19.01
87.		Сравнение целых чисел		20.01
88.		Сравнение целых чисел		21.01
89.		Сложение целых чисел		22.01
90.		Сложение целых чисел		23.01
91.		Сложение целых чисел		26.01
92.		Вычитание целых чисел		27.01
93.		Вычитание целых чисел		28.01
94.		Умножение целых чисел		29.01
95.		Умножение целых чисел		30.01
96.		Деление целых чисел		2.02
97.		Деление целых чисел		3.02
98.		Вычисление с целыми числами		4.02
99.		Вычисление с целыми числами		5.02
100.		Вычисление с целыми числами		6.02
101.		Вычисление с целыми числами		9.02
102.		Обобщающее повторение по теме «Целые числа»		10.02
103.		Контрольная работа №6. «Целые числа»		11.02					Используют разные приемы проверки правильности ответа
Глава VII. Рациональные числа ( 27 ч)
104.		Анализ контрольной работы. Отрицательные дроби. Рациональные числа				12.02			Положительные числа, отрицательные числа, множество целых чисел. Модуль числа. Противоположные числа. Сравнение рациональных чисел. Правила сложения, вычитания, умножения и деления противоположных чисел, отрицательных чисел и чисел с разными знаками. Координатная плоскость, ордината, абсцисса, начало координат, оси координат, декартовая система координат, четверть. Симметрия, симметрия относительно точки, относительно прямой, симметричные фигуры.		Иметь представление о рациональных числах и действиях над ними. Уметь проводить самооценку собственных действий Иметь представление о сравнении чисел на координатной прямой, о неравенстве с модулем, о сравнении чисел. Уметь давать оценку информации, фактам, процессам. Определять их актуальность. Иметь представление о правилах вычисления алгебраической суммы, о модуле суммы, о противоположных числах. Уметь найти несколько способов решения, аргументировать рациональный способ, проводить доказательные рассуждения. Уметь: находить расстояние между точками на координатной прямой. вычисляя модуль разности; давать оценку информации, фактам, процессам, определять их актуальность. Знать правило умножения отрицательных чисел, распределительного закона относительно вычитания. Уметь воспринимать устную речь участвовать в диалоге, понимать точку зрения собеседника, подбирать аргументы для ответа на поставленный вопрос. Приводить примеры. Иметь представление о правилах делении чисел разного знака Уметь проводить самооценку собственных действий		Л3, Л6, Л9, М3, М6, М10, М17, М20, М21, М28, П1, П2, П8
105.		Отрицательные дроби. Рациональные числа				13.02
106.		Модуль рационального числа				16.02
107.		Сравнение рациональных чисел				17.02
108.		Сравнение рациональных чисел				18.02
109.		Сложение рациональных чисел				19.02
110.		Сложение рациональных чисел				20.02
111.		Вычитание рациональных чисел				23.02
112.		Вычитание рациональных чисел				24.02
113.		Умножение рациональных чисел				25.02
114.		Умножение рациональных чисел				26.02
115.		Деление рациональных чисел				27.02
116.		Деление рациональных чисел				2.03
117.		Координатная плоскость				3.03
118.		Координатная плоскость				4.03
119.		Координатная плоскость				5.03
120.		Симметрия относительно прямой				6.03
121.		Построение симметричной прямой				9.03
122.		Примеры на все действия с рациональными числами				10.03
123.		Построение в координатной плоскости				11.03
124.		Решение задач на сложение и вычитание рациональных чисел				12.03
125.		Решение задач на умножение и деление рациональных чисел				13.03
126.		Решение уравнений				16.03
127.		Обобщающее повторение по теме «Рациональные числа»				17.03
128.		Контрольная работа № 7. «Рациональные числа»				18.03
129.		Итоговый тест за 3 четверть				19.03			Используют разные приемы проверки правильности ответа
130.		Анализ контрольной работы				20.03
Раздел IV. Понятие о действительных числах (30 ч) Глава VIII. Понятие о действительных числах (11 ч)
131.		Входной тест				1.04
132.		Бесконечные периодические десятичные дроби				2.04			Бесконечные периодические десятичные дроби. Рациональные числа как периодические десятичные дроби; преобразование периодической дроби в обыкновенную. Бесконечные непериодические десятичные дроби; иррациональные числа. Сравнение бесконечных десятичных дробей; приближённые вычисления с бесконечными десятичными дробями. Измерение отрезка; длина отрезка- действительное число. Число «Пи»; длина окружности; площадь круга		Запись числа в виде периодической дроби; Преобразование периодической десятичной дроби в обыкновенную и наоборот. Сравнивать и упорядочивать десятичные дроби; выполнять вычисления с десятичными дробями. Вычисление длины окружности, диаметр; вычисление площади круга, радиуса.		Л6, Л7, Л10, М2, М5, М12, М15, М16, М21, М32, П1, П2, П4, П8
133.		Бесконечные периодические десятичные дроби				3.04
134.		Бесконечные непериодические десятичные дроби. Действительные числа				6.04
135.		Сравнение действительных чисел				7.04
136.		Приближенные вычисления с действительными числами				8.04
137.		Длина отрезка				9.04
138.		Длина окружности. Площадь круга				10.04
139.		Решение задач				13.04
140.		Контрольная работа № 8 «Действительные числа»				14.04			. Используют разные приемы проверки правильности ответа
141.		Анализ контрольной работы				15.04
Глава IX. Геометрические и комбинаторные задачи ( 19 ч)
142.		Геометрия на клетчатой бумаге		16.04					Прямые разметки; узлы; прямая на клетчатой бумаге; площадь треугольника с вершинами в узлах; количество узлов на диагонали прямоугольника. Домино, тримино, тетрамино, пентамино; количество фигур тримино; количество фигур тетрамино; шахматная раскраска Правило умножения; сложный выбор для элементов одного множеств; факториал; количество разных троек на множестве из n элементов; вычисление вероятностей. Многогранники; пирамида; призма. Примеры развёрток многогранников Сечение многогранников; построение сечений. Используют разные приемы проверки правильности ответа		Уметь вычислять площадь треугольника; изображать геометрические фигуры на клетчатой бумаге с использованием её свойств. Уметь изображать равные фигуры; симметричные фигуры; конструировать орнаменты и паркеты, изображая их с помощью инструментов. Уметь вычислять вероятность событий; выполнять перебор всех возможных вариантов для перерасчёта объектов или комбинаций, выделять комбинации, отвечающие заданным условиям. Знать способы решения задач на нахождение длин отрезков, периметров многоугольников. Уметь распознавать развёртки многогранников. Уметь определять вид простейших сечений пространственных фигур, получаемых путём предметного или компьютерного моделирования.		Л1, Л2, Л8, Л11, М5, М16, М21, П2, П9,
143.		Геометрия на клетчатой бумаге		17.04
144.		Геометрия на клетчатой бумаге		20.04
145.		Задачи на разрезание и составление фигур		21.04
146.		Задачи на разрезание и составление фигур		22.04
147.		Задачи на разрезание и составление фигур		23.04
148.		Решение задач на перебор вариантов		24.04
149.		Решение задач на вычисление вероятностей		27.04
150.		Решение задач на вычисление вероятностей		28.04
151.		Многогранники		29.04
152.		Отпечатки многогранников		30.04
153		Развертки многогранников		4.05
154		Развертки многогранников		5.05
155		Понятие о сечении многогранника		6.05
156.		Обобщающее повторение по теме «Геометрические и комбинаторные задачи»		7.05
157.		Контрольная работа № 9 «Геометрические и комбинаторные задачи»		8.05
158		Анализ контрольной работы		11.05
159.		Решение задач		12.05
160		Итоговый тест за 4 четверть		13.05
Повторение (10 ч)
161		Десятичные дроби.		14.05					Отработка знаний и умений, приобретенных на предыдущих уроках.		Иметь представление об обыкновенных и десятичных дробях. Знать свойства арифметических действий. Уметь выполнять арифметические действия с указанными числами. Решение задач.		Л1, Л6, М4, М8, М10, М30, П10, П4
162		Отношения и пропорции. Проценты.		1505
163		Целые числа		18.05
164.		Рациональные числа.		19.05
165.		Действительные числа.		20.05
166.		Элементы геометрии.		21.05
167.		Геометрические и комбинаторные задачи.		22.05
168		Итоговый тест за курс 6 класс		25.05					Используют разные приемы проверки правильности ответа
169.		Анализ работы		26.05
170.		Итоговый урок		28.05