16
Муниципальное бюджетное образовательное учреждение
средняя общеобразовательная школа №1 г. Павлово
Рассмотрено Рассмотрено РЭС Утверждаю:
на заседании ШЭС ______________________ директор МБОУ СОШ №1
протокол № _______ от «____» __________ 201___ г __________ /Кузина Т.А./ «____» __________ 201___ г. «____» __________ 201___ г.
Программа элективного курса
«Избранные вопросы математики»
9 класс
Составитель:
Учитель математики Капитанова О.В.
г. Павлово
2012 г.
Введение
Важное направление модернизации среднего образования – переход к профильному обучению, необходимость которого определена в «Концепции профильного обучения на старшей ступени общего образования».
Модель общеобразовательного учреждения с профильным обучением на старшей ступени предусматривает возможность разнообразных комбинаций учебных предметов, введение элективных курсов - обязательных для посещения курсов по выбору учащихся, входящих в состав профиля обучения на старшей ступени школы.
Элективные курсы – обязательные курсы, которые учащиеся выбирают сами, из имеющегося в учебном заведении комплекта и входящие в состав профиля на старшей ступени школы. Эти курсы реализуются за счет школьного компонента образования.
Элективный курс по предпрофильной подготовке учащихся 9 классов посвящён избранным вопросам математики. Данный элективный курс рассчитан в первую очередь на учащихся, желающих расширить и углубить свои знания по математике, сделать правильный выбор профиля обучения в старших классах и качественно подготовиться к ЕГЭ. Он поможет школьникам систематизировать полученные на уроках знания и открыть для себя новые методы решения некоторых задач, которые не рассматриваются в рамках школьной программы.
Пояснительная записка
Элективный курс «Избранные вопросы математики» направлен на расширение знаний учащихся, повышение уровня математической подготовки через решение большого класса задач. Наряду с основной задачей обучения математики – обеспечением прочного и сознательного овладения учащимися системы математических знаний и умений, данный курс предусматривает формирование устойчивого интереса к предмету, выявление и развитие математических способностей, ориентацию на профессии, существенным образом связанные с математикой, выбору профиля дальнейшего обучения.
Курс включает в себя несколько тем, общей продолжительностью 17 часов. Это:
Решение текстовых задач.( 4 часа)
Решение уравнений и неравенств с модулем. (4 часа)
Задачи линейных и квадратных уравнений и неравенств с параметрами.
Решение задач в целых числах. (4 часа)
Такой подбор материала преследует две цели. С одной стороны, это создание базы для развития способности учащихся, с другой – восполнение некоторых содержательных пробелов основного курса. Учащиеся испытывают затруднения при решении ряда сложных задач. К ним относятся текстовые задачи, уравнения и неравенства, содержащие модуль, уравнения и неравенства с параметрами, а также задачи, которым очень мало уделяется внимания в средней школе: это задачи в целых числах
.
Цель курса:
Изучение этого курса позволяет решить следующие задачи:
формировать аналитическое мышление, развивать память, кругозор, умение преодолевать трудности при решении сложных задач
Одна из целей обучения математике - научить учащихся решать задачи. Одно из средств повышения эффективности обучения математике - систематическое и целенаправленное формирование умений решать задачи. Решение задач выступает и как цель и как средство обучения. Умение решать задачи является одним из основных критериев уровня математического развития обучающихся. В ходе работы над задачами формируется творческое мышление.
Текстовые алгебраические задачи (иначе, задачи на составление уравнений) представляют собой раздел математики, традиционно предлагаемый на вступительных экзаменах в вузах, в централизованном тестировании, в контрольных измерительных материалах ЕГЭ. Решение этих задач связано с развитием логического мышления, сообразительности, наблюдательности, и часто требуют и непростых преобразований, возникающих при решении полученных систем уравнений и неравенств. Текстовые задачи, как правило, вызывают трудности. Это происходит от недостаточного внимания, уделяемого такого рода задачам в школьном курсе математики. Данный курс - это попытка восполнить этот пробел. При изучении данного раздела осуществляются межпредметные связи. Так при изучении задач на смеси и сплавы можно использовать знания, полученные на уроках химии, а при изучении задач на работу, движение – материал уроков физики. Также в данном разделе используются некоторые экономические понятия ( процент, вклад и т.д.).
Полный минимум знаний, необходимый для решения всех типов текстовых задач, формируется в течение первых девяти лет обучения учащихся в школе, поэтому представленный элективный курс «Текстовые задачи» рекомендуется вводить с 9-го класса.
Тема «Решение уравнений и неравенств содержащие модуль» является одной из важнейших и самых трудных для усвоения учащимися тем курса школьной математики. Программой школьного курса математики не предусмотрены обобщение и систематизация знаний о модулях, их свойствах, полученных учащимися за весь период обучения. Поэтому и возникла необходимость включить в элективный курс этот раздел. Изучение свойств модуля и решение различных задач с применением абсолютной величины целесообразно продолжить и на элективных курсах в последующих классах, чтобы на разных ступенях обучения дети изучали один и тот же материал, но разного уровня сложности.
Понятие модуля широко применяется не только в различных разделах школьного курса математики, но и в курсах высшей математики, физики и технических наук, изучаемых в вузах. Задачи, связанные с абсолютными величинами, часто встречаются на математических олимпиадах и на ЕГЭ.
Курс позволит школьникам систематизировать, расширить и укрепить знания, связанные с абсолютной величиной, подготовиться для дальнейшего изучения тем, использующих это понятие, научиться решать разнообразные задачи различной сложности, способствует выработке и закреплению навыков работы на компьютере.
Одной из тем курса является тема «Задачи с параметрами». Задачи такого типа вызывают затруднения у учащихся, так как практических заданий по данной теме в школьных учебниках мало. К «встрече» с такими задачами при сдаче Единого государственного экзамена надо готовиться. И готовиться нужно начинать с 8-9 классов.
Для решения таких задач не требуется обладать знаниями, выходящими за рамки школьной программы. Однако непривычность формулировки обычно ставит в тупик учащихся, не имеющих опыт решения подобных задач.
Решение уравнений и неравенств с параметрами, открывает перед учащимися значительное число эвристических приемов общего характера, ценных для математического развития личности, применяемых в исследованиях. Учащиеся, владеющие методами решения задач с параметрами, успешно справляются и с другими задачами. Это связано с тем, что решение задач с параметром требует не только знания свойств функций и уравнений, умений выполнять алгебраические преобразования, но также высокой логической культуры и хорошей техники исследования. Задачи с параметрами способствуют формированию логического мышления и повышению математической культуры школьников.
Для успешного решения таких задач необходимо рассматривать различные случаи (и понимать, какие именно случаи нужно рассмотреть), что приучает к внимательности и аккуратности. Даже при записи ответа нужно быть предельно сосредоточенным, чтобы не упустить ни одной из частей его, полученных в ходе решения. Подчас задачи с параметрами требуют довольно тонких логических рассуждений.
Учиться решать задачи с параметрами нужно, начиная с простейших. Обычно в качестве таковых используются линейные уравнения и неравенства с параметрами и задачи, связанные с квадратным трёхчленом. Данный раздел элективного курса затрагивает вопросы о существовании корней линейных и квадратных уравнений, их количестве, расположении на числовой прямой.
Наиболее трудным вопросом школьной математики традиционно является вопрос решения задач в целых числах. В связи с этим, учащимся будет небезынтересно познакомиться с методами решения некоторых уравнений в целых числах, тем более, что в программе единого государственного экзамена и на олимпиадах разного уровня часто предлагаются задания, предполагающие решение какого-либо уравнения в целых числах. Решение различного вида уравнений является одной из содержательных линий школьного курса математики, но при этом, методы решения уравнений с несколькими неизвестными практически не рассматриваются. При этом для решения таких задач не требуется никаких специальных знаний.
Вместе с тем, решение уравнений от нескольких неизвестных в целых числах является одной из древнейших математических задач. Большинство методов решения таких уравнений основаны на теории делимости целых чисел, интерес к которой в настоящее время определяется бурным развитием информационных технологий.
После рассмотрения полного курса учащиеся должны иметь следующие результаты обучения:
Знать:
понятия параметр, задача с параметром, абсолютная величина, модуль, процент, задача на работу, задача на движение, задача на процентное отношение, уравнение в целых числах;
методы решения различных текстовых задач;
алгоритмы решения уравнений, неравенств, систем уравнений и неравенств, содержащих переменную под знаком модуля.
правила построения графиков функций, содержащих знак абсолютной величины;
методы решения базовых видов задач с параметрами (линейное уравнение, квадратное уравнение, линейное неравенство);
методы решения различных уравнений в целых числах;
Уметь:
уметь применять полученные математические знания в решении жизненных задач;
уметь определять тип текстовой задач;
преобразовывать выражения, содержащие модуль;
строить графики элементарных функций, содержащих модуль.
решать линейные уравнения, неравенства, квадратные уравнения с параметрами;
применять алгоритмический подход к решению задач с параметрами;
решать простейшие уравнений в целых числах, используя имеющиеся алгоритмы;
точно, сжато выражать математическую мысль в устном и письменном изложении, использовать символику;
уверенно владеть знаниями и применять их к решению задач;
анализировать, систематизировать, объединять рассматриваемые задачи;
писать рефераты, доклады, оформлять их;.
самостоятельно работать с таблицами, дополнительной и справочной литературой;
составлять алгоритмы решения типичных задач;
применять изученные алгоритмы для решения соответствующих заданий;
Особенности курса:
Краткость изучения материала.
Практическая значимость для учащихся.
Нетрадиционные формы изучения материала.
Курс предназначен для учащихся 9 классов средних общеобразовательных учреждений, реализующих предпрофильную подготовку. Рассчитан на 17 часов аудиторного времени, по одному часу в неделю во втором полугодии.
В курсе заложена возможность дифференцированного обучения, как путём использования задач различного уровня сложности, так и на основе различной степени самостоятельности осваивания нового материала.
Изучение материала предполагается построить в виде лекций, практических занятий,
семинаров. В рамках преподавания наряду с лекциями и семинарами предусматривается активное использование элементов проблемного обучения. Доминирующей формой обучения должна стать поисково-исследовательская деятельность обучающихся, реализация которой осуществляется как в рамках уроков, так и в ходе выполнения домашних заданий.
На занятиях предполагается активный диалог с учащимися. Школьники, изучившие данный материал, смогут применить его при решении конкурсных, прикладных задач, а также использовать в повседневной жизни в практических целях.
В качестве текущего контроля в каждом разделе курса применяется рейтинговая оценка знаний. Форма итогового контроля в конце каждой части курса – зачёт, тестирование или выполнение практической работы (реферат, презентация, исследовательская работа, проект).
По окончании курса учащийся защищает проект, реферат, получает сертификат, которым сможет пополнить свой «портфолио».
Учебно-тематическое планирование.
| № | Наименование разделов | Всего часов | Вид контроля |
|
| I. Текстовые задачи. | 4 | Самостоятельные работы, тесты |
| 1 | Задачи на движение | 1 |
| 2 | Задачи на работу и производительность | 1 |
| 3 | Решение задач, связанные с определением массовой (объемной) концентрацией вещества. | 1 |
| 4 | Решение сложных задач на смеси и сплавы | 1 |
|
| II. Решение уравнений и неравенств с модулем. | 4 | Самостоятельные работы, тесты, презентации, исследовательские работы |
| 5 | Геометрическая интерпретация понятия модуля. Модуль разности модулей двух чисел. Модуль произведения и модуль частного. | 1 |
| 6 | Графики функций, аналитическое выражение которых содержит знак абсолютной величины | 1 |
| 7 | Уравнения, содержащие абсолютные величины. Метод интервалов при решении уравнений, содержащих абсолютные величины. | 1 |
| 8 | Неравенства с одним неизвестным. Основные методы решения неравенств с модулем. Метод интервалов при решении неравенств, содержащих знак модуля. | 1 |
|
| III. Решение линейных и квадратных уравнений и неравенств с параметрами. | 5 | Самостоятельные работы, проекты, исследовательские работы |
| 9 | Линейные уравнения с параметром. Алгоритм решения линейных уравнений с параметром. | 1 |
| 10 | Системы линейных неравенств с параметрами. | 1 |
| 11 | Дробно - рациональные уравнения с параметром. | 1 |
| 12-13 | Квадратные уравнения с параметром. Теорема Виета. | 2 |
|
| IV. Решение задач в целых числах. | 4 | Самостоятельные работы, проекты, презентации, рефераты |
| 14 | Проблема решения уравнений в целых числах: от Диофанта до доказательства теоремы Ферма | 1 |
| 15 | Отношение делимости на множестве целых чисел. Простые и составные числа. Основная теорема арифметики. Пифагоровы тройки. | 1 |
| 16 | Наибольший общий делитель целых чисел. Теорема о делении с остатком. Алгоритм Евклида | 1 |
| 17 | Различные методы решения диофантовых уравнений первой степени с двумя переменными. | 1 |
Содержание программы
Тема I. Решение текстовых задач. (4 часа)
Задачи на движение. Понятия равномерного прямолинейного и равноускоренного движения. Основные формулы, необходимые для решения задач на равномерное прямолинейное движение и равноускоренное движение. Задачи на движение по реке.
Задачи на работу и производительность
Решение задач, связанные с определением массовой (объемной) концентрацией вещества.
Решение сложных задач на смеси и сплавы
Тема II. Решение уравнений и неравенств с модулем. (4 часа)
Геометрическая интерпретация понятия модуля. Модуль суммы и модуль разности конечного числа действительных чисел. Модуль разности модулей двух чисел. Модуль произведения и модуль частного. Операции над абсолютными величинами. Упрощение выражений, содержащих переменную под знаком модуля.
Графики функций, аналитическое выражение которых содержит знак абсолютной величины
Уравнения, содержащие абсолютные величины. Основные методы решения уравнений с модулем. Раскрытие модуля по определению, переход от исходного уравнения к равносильной системе, возведение в квадрат обеих частей уравнения, метод интервалов, графический метод, использование свойств абсолютной величины. Метод замены переменных при решении уравнений, содержащих абсолютные величины. Метод интервалов при решении уравнений, содержащих абсолютные величины.
Неравенства с одним неизвестным. Основные методы решения неравенств с модулем. Метод интервалов при решении неравенств, содержащих знак модуля. Неравенства с параметрами, содержащие абсолютные величины.
Тема III. Решение линейных и квадратных уравнений и неравенств с параметрами.
Линейные уравнения с параметром. Алгоритм решения линейных уравнений с параметром. Нахождение значений параметра, при каждом из которых решения уравнений удовлетворяют заданным условиям.
Системы линейных неравенств и уравнений.
Дробно - рациональные уравнения с параметром Определение дробно – рационального уравнения с параметром. Решение дробно - рациональных уравнений с параметром. Исследование количества корней в зависимости от значений параметра.
Квадратные уравнения с параметром. Определение квадратного уравнения с параметром. Решение квадратных уравнений с параметром. Нахождение значений параметра, при каждом из которых решения уравнений удовлетворяют заданным условиям. Теорема Виета.
Тема IV. Решение задач в целых числах. (4 часа)
Проблема решения уравнений в целых числах: от Диофанта до доказательства теоремы Ферма
Отношение делимости на множестве целых чисел. Простые и составные числа. Основная теорема арифметики.
Наибольший общий делитель целых чисел.
Теорема о делении с остатком. Алгоритм Евклида
Различные методы решения диофантовых уравнений первой степени от двух переменных.
Пифагоровы тройки.
Методы решения некоторых нелинейных неопределенных уравнений.
Литература.
Для учащихся:
Мордкович. А.Г. Алгебра 9кл. Задачник для общеобразовательных учреждений, М.: Мнемозина, 2008 г.
Айвазян Д.Ф. Математика. Решение уравнений и неравенств с параметрами: элективный курс.- Волгоград: Учитель, 2009 г.
Мичасова М.А. , Малышев И.Г., Иванов Б.Н. Теоретические и практические вопросы подготовки к ЕГЭ по математике.-Н.Новгород: НИРО, 2009.
Мичасова М.А. , Малышев И.Г., Иванов Б.Н. Подготовка к ЕГЭ по математике. Задания С1-С6. -Н.Новгород: НИРО, 20010
Для учителя:
Мордкович. А.Г. Алгебра 9кл. Задачник для общеобразовательных учреждений, М.: Мнемозина, 2008 г.
Горнштейн П.И. и др. Задачи с параметрами. - М., Илекса, 2007
Мордкович А.Г. Алгебра 8. Задачник для общеобразовательных учреждений. - М.Мнемозина, 2007.
Айвазян Д.Ф. Математика. Решение уравнений и неравенств с параметрами: элективный курс.- Волгоград: Учитель, 2009 г.
Студенецкая В.Н. Сагат6елова Л.С. Сборник элективных курсов. Математика. 8-9 классы.-Волгоград:Учтитель,2006 .
Мичасова М.А. , Малышев И.Г., Иванов Б.Н. Теоретические и практические вопросы подготовки к ЕГЭ по математике.-Н.Новгород: НИРО, 2009.
Мичасова М.А. , Малышев И.Г., Иванов Б.Н. Подготовка к ЕГЭ по математике. Задания С1-С6. -Н.Новгород: НИРО, 20010
Харламов Л.Н.. Элективные курсы по математике. 8-9 класс.- Волгоград: Учитель, 2007.
Фарков А.В. Математические олимпиады в школе. 5-11 классы. М.: Фйрис-пресс, 2006г.
Фоминых, Ю.Ф. Диофантовы уравнения //Математика в шк. – 1996. - №6.
Перельман, Я.И. Занимательная алгебра. – М.: Наука, 1975.
Методическое обеспечение темы «Текстовые задачи».
Самостоятельная работа №1.
| Вариант 1. | Вариант 2. |
| 1) Лодка может проплыть 15 км по течению реки и еще 6 км против течения за то же время, за какое плот может проплыть 5 км по этой реке. Найдите скорость течения реки, если известно, что собственная скорость лодки 8 км/ч. | 1) Катер проплывает 20 км против течения реки и еще 24 км по течению за то же время, за какое плот может проплыть по этой реке 9 км. Скорость катера в стоячей воде равна 15 км/ч. Найдите скорость течения реки.
|
| 2) Ирина рассчитала, что сможет хорошо подготовиться к зачету по английскому языку, если будет заучивать по 24 слова в день. Однако ежедневно она выучивала дополнительно 6 слов, и уже за 2 дня до зачета ей осталось выучить 18 слов. Сколько слов должна была выучить Ирина?
| 2) Николай рассчитал, что он сможет хорошо подготовиться к экзамену, если будет решать по 12 задач в день. Однако ежедневно он перевыполнял свою норму на 8 задач и уже за 5 дней до экзамена решил на 20 задач больше, чем планировал первоначально. Сколько задач решил Николай? |
| 3) Четыре бригады должны разгрузить вагон с продуктами. Вторая, третья и четвертая бригады вместе могут выполнить эту работу за 4 ч; первая, третья и четвертая — за 3 ч. Если же будут работать только первая и вторая бригады, то вагон будет разгружен за 6 ч. За какое время могут разгрузить вагон все четыре бригады, работая вместе?
| 2) Для откачивания воды из резервуара имеется четыре насоса. Если включить первый, второй и третий насосы, то работа будет выполнена за 10 мин; если включить первый, третий и четвертый насосы, то та же работа будет выполнена за 12 мин. Если же будут работать только два насоса, второй и четвертый, то работа будет выполнена за 15 мин. За какое время можно откачать воду из резервуара при помощи всех четырех насосов?
|
| 4) Абрикосы при сушке теряют 60% своей массы. Сколько процентов воды содержат свежие абрикосы, если в сушеных абрикосах 25% воды?
| 4) В свежих яблоках 80% воды, а в сушеных—20%. На сколько процентов уменьшается масса яблок при сушке?
|
| 5) Имеется руда из двух пластов с содержанием меди в 6% и 11%. Сколько «бедной» руды нужно взять, чтобы при смешивании с «богатой» получить 20 тонн с содержанием меди 8%? | 5) Имеется два сплава с разным содержанием меди: в первом содержится 70%, а во втором — 40% меди. В каком отношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий 50% меди?
|
| 6) Мотоцикл, движущийся по шоссе со скоростью 60 км/ч, миновал пост ДПС. Через час мимо этого поста проехал автомобиль со скоростью 90 км/ч. На каком расстоянии от поста ДПС автомобиль догнал мотоцикл, если оба они ехали без остановок?
| 6) Николай и Андрей живут в одном доме. Николай вышел из дома и направился к школе. Через 4 мин после него из дома вышел Андрей и догнал своего друга у школы. Найдите расстояние от дома до школы, если Николай шел со скоростью 60 м/мин, а скорость Андрея 80 м/мин.
|
Методическое обеспечение темы «Решение линейных и квадратных уравнений с параметром»
Проект 1. «Исследование линейных уравнений с параметром»
Исследуйте уравнения по схеме:
Привести уравнение к виду: ах = b
Найти контрольные значения параметра из условия: а=0.
Исследовать уравнение при разных значениях параметра. (при а=0 и при а≠0), подставляя эти значения в уравнение.
1. Решить уравнение
(b2 + 4b)х = 2 b+ 8;
ах = а3 – а;
6х + 6 = 5b - 2х;
(а - З)3 х + 4 (а - 1) = 8 + (а - 1)(а - 3)х;
|5х-3| - 7 = а;
׀5х-3| - 7 = а;
2. Найти все значения параметра а, при которых уравнение а2х = а (х + 2) - 2 не имеет решений.
5. Найти все значения параметра а, при которых уравнена (а2 - а) х = а2 + 6а не имеет решений.
Проект 2. «Исследование линейных уравнений с параметром при наличии дополнительных условий »
Исследуйте уравнения по схеме:
Привести уравнение к виду: ах = b
Найти контрольные значения параметра из условия: а=0.
Исследовать уравнение при разных значениях параметра. (при а=0 и при а≠0), подставляя эти значения в уравнение.
Задания:
Решить уравнение (2а+1)х=3а+(а-2)х и найти значения параметра, при которых корень этого уравнения- число положительное.
Найти значение параметра а, при котором уравнение а(2а+3)х+а2=а2х+3а имеет единственный отрицательный корень.
При каком значении параметра b уравнение (х-b+1)2-(х+b-1)2=2х+6 имеет:
положительный корень;
отрицательный корень
корень, равный 0.
Определите. При каком условии уравнение
(Ь + х)а =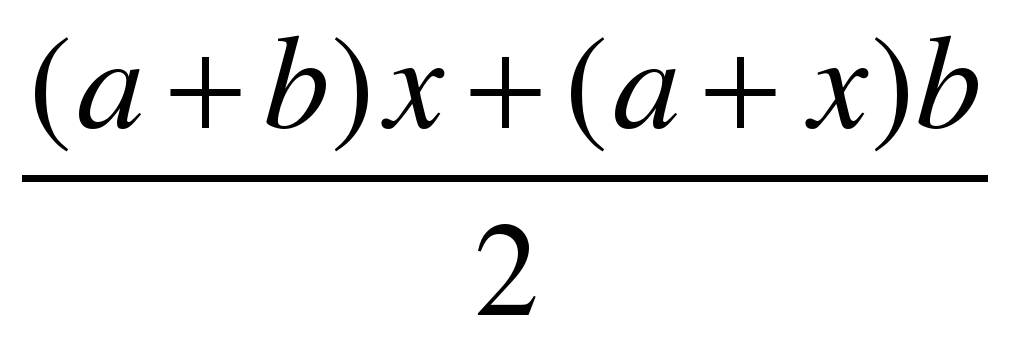
имеет единственное решение;
имеет бесконечно много корней;
не имеет корней
При каком значении параметра а уравнение а(х-1)=х-2 имеет решение, удовлетворяющее условию х1
Проект3. «Исследование линейных систем с параметром»
Линейная система двух уравнений с двумя неизвестными вида 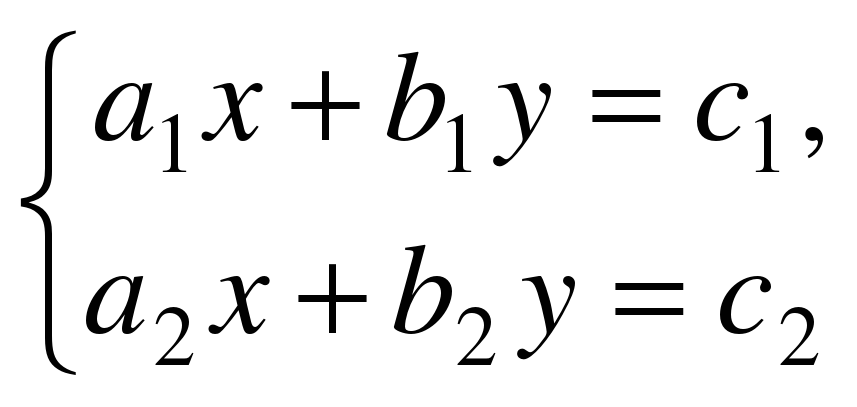 имеет единственное решение, если коэффициенты при неизвестных не пропорциональны. Условие пропорциональности удобно записать так:
имеет единственное решение, если коэффициенты при неизвестных не пропорциональны. Условие пропорциональности удобно записать так:  Исследуйте системы по схеме:
Исследуйте системы по схеме:
Сначала определите, при каких значениях параметра  система имеет единственное решение;
система имеет единственное решение;
Затем найдите эти решения (они будут зависеть от  );
);
Далее отдельно разберите случай исключительных значений  , подставляя эти значения в систему.
, подставляя эти значения в систему.
А)  Б)
Б) 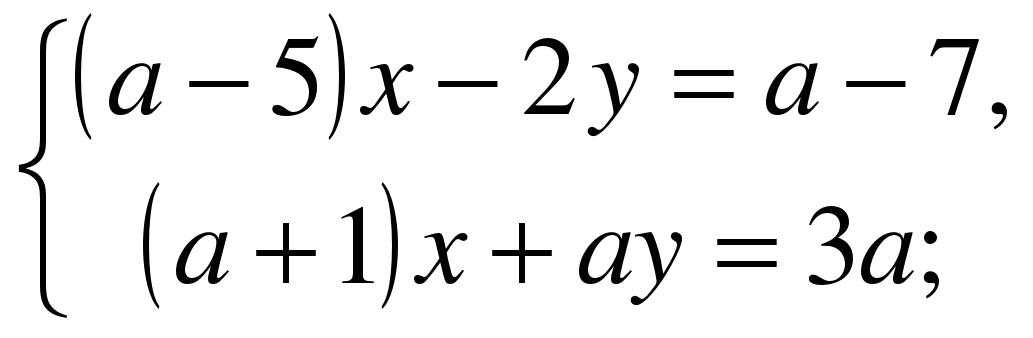
В) 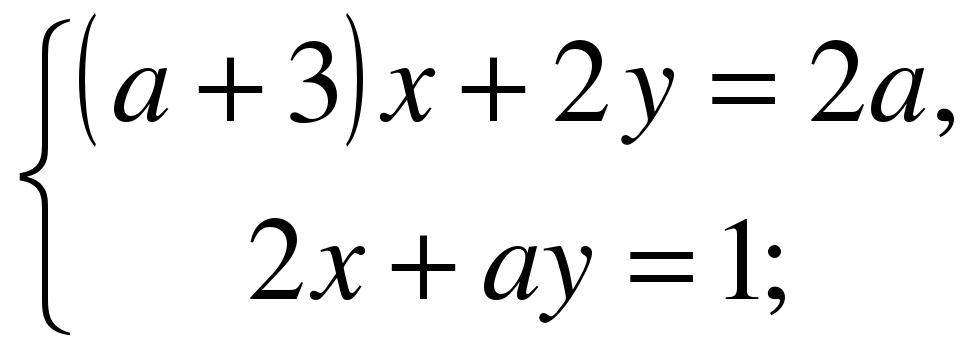 Г)
Г) 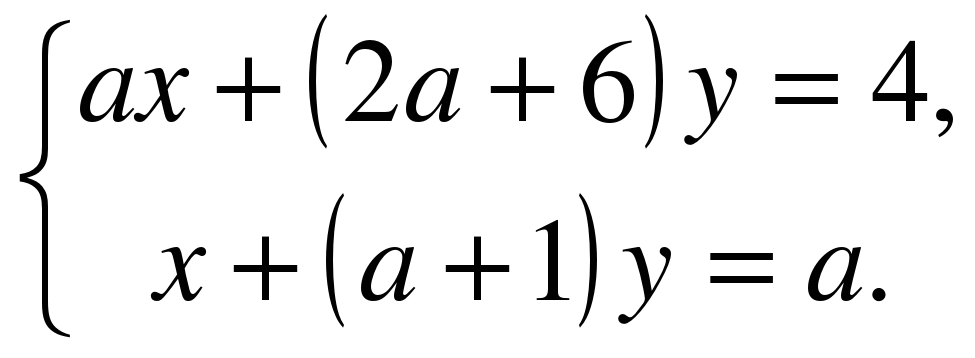
Проект 4. «Исследование линейных неравенств с параметром»
Привести неравенство к виду: ах(
Исследовать неравенство по схеме:

Решить неравенства:
mх + 1 2(х- 1);
mх — 2х -3;
(m-2)х -3;
2а {а- 2)х а-2;
2mх-1
2m - х 1 + mх;
b2x -bxb2+b-2;
2х + 13 ах + 17;
 + х
+ х
 ;
;
mх — х + 1 m ;
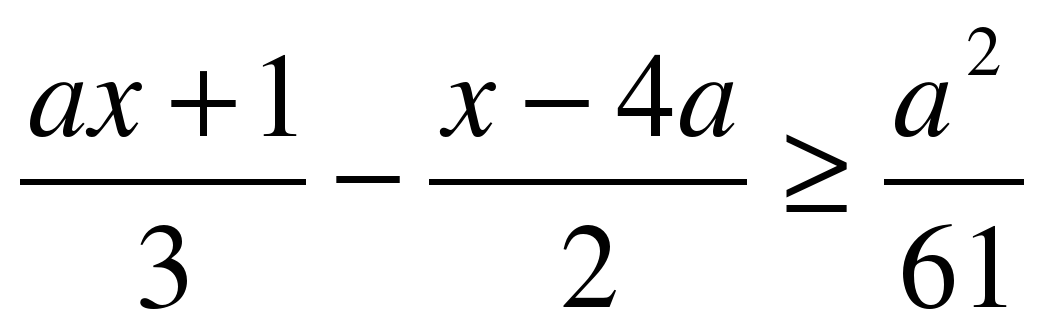
Проект 5. «Исследование систем линейных неравенств с параметром»
1. При каких значениях параметра а система неравенств имеет хотя бы одно решение:
а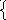 ) x
) x
ха;
б ) х≥2
) х≥2
x
2. Существуют ли такие значения а, при которых решением системы неравенств
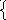 х3 является промежуток:
х3 является промежуток:
ха
а) (5;+∞)?
б) [-3; +оо)?
3. Решите неравенство |х — 3|
4. При каких значениях а неравенство справедливо при любом значении х:
а) |х| а; б) а׀х׀ - 1 0?
Исследовательская работа 1. «Исследование решений квадратных уравнений с параметром»
Исследовать решение уравнений в зависимости от параметра.
а) x2+(3b-2)x-6b = 0;
б) х2 - (За - 2)х + 2а2 - а - 3 = 0;
в) ах2 -(а + 1)х + 1 = 0;
г) (а +1)х2 -2х-+1-а = 0;
д) abx2 +{а2+ b2 )х + ab = 0;
е) abx2 +(а2 -b2)x + (a-b)2 = 0.
Исследовательская работа 2. «Использование теоремы Виета при решении квадратных уравнений с параметром»
Известно, что корни сумма квадратов корней уравнения х2+рх+20=0 равна 104. исследовать корни уравнения и коэффициент р.
Один из корней уравнения х2-(2а+1)х+а2=0 в 9 раз больше другого. Исследовать все значения параметра а.
Определить все значения параметра а, при которых уравнение 2х2-(а+1)х+(а-1)=0 имеет два корня, разность которых равна их произведению.
Определить все значения параметра а, при которых корни уравнения
(а-2)х2-2ах+а+3=0 положительны. Найти количество целых значений параметра, удовлетворяющих условию ׀а׀≤10.
5. Определить все значения параметра а, при котором корни уравнения х2-2х+а=0 удовлетворяют условию 7х1-4х2=47.
6. При каких значениях параметра р сумма корней квадратного уравнения
х2+(р2+4р-5)х-р=0 равна 0.
Исследовательская работа 3. «Расположение корней квадратного уравнения в зависимости от параметра»
При каких значениях параметра с оба корня квадратного уравнения
х2+4сх+(1-2с+4с2)=0 различны и меньше, чем -1.
При каких действительных значениях к оба корня уравнения (1+к)х2-3кх+4к=0 больше 1.
1.При каких значениях параметра а оба корня уравнения х2 - 6ах + 2а + 9а2 = 0 больше 3?
При каких значениях параметра а оба корня уравнения
(2 - а)х2 - Зах + 2а = 0 больше ½?
При каких значениях параметра а оба корня уравнения ах2- 2(2а- 1)х + 2 - За = 0 больше 1?
Самостоятельная работа №1.
Решить уравнения:
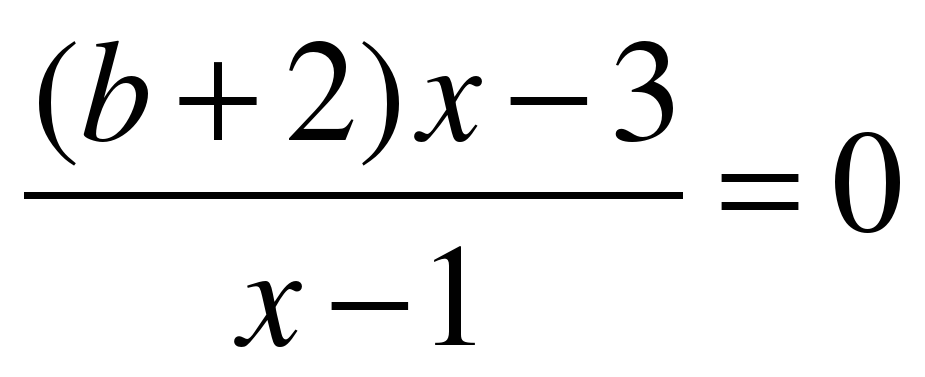
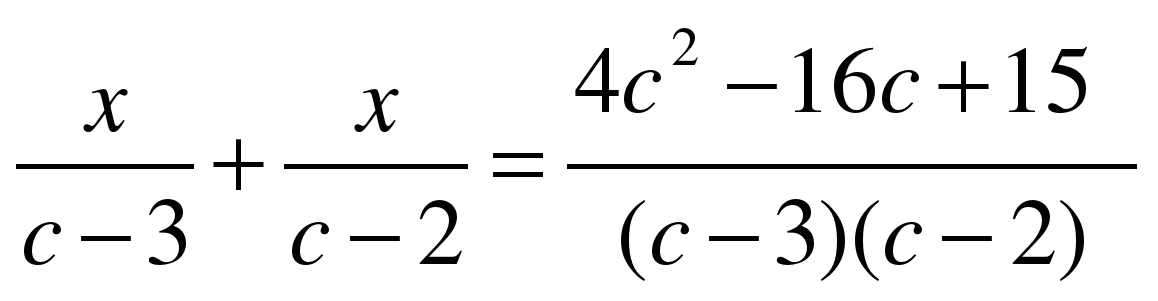
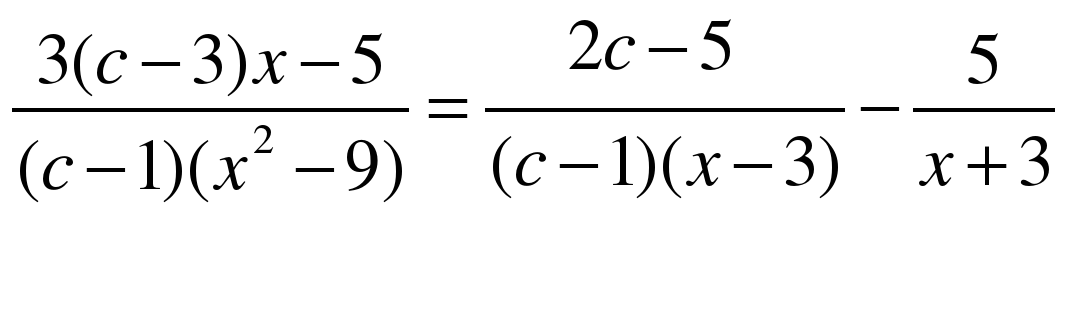
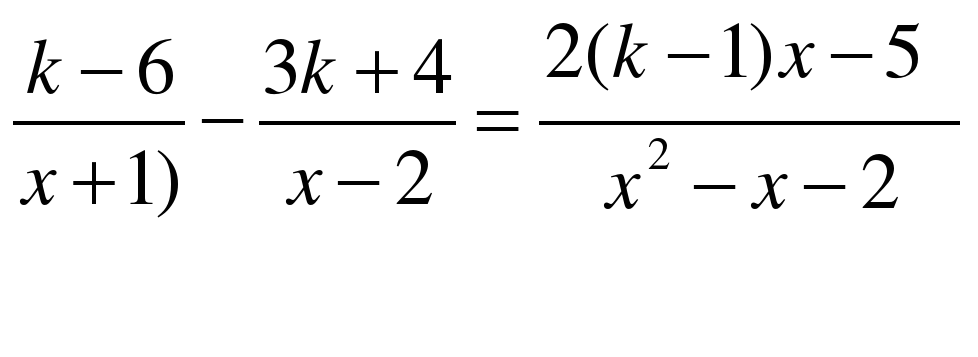
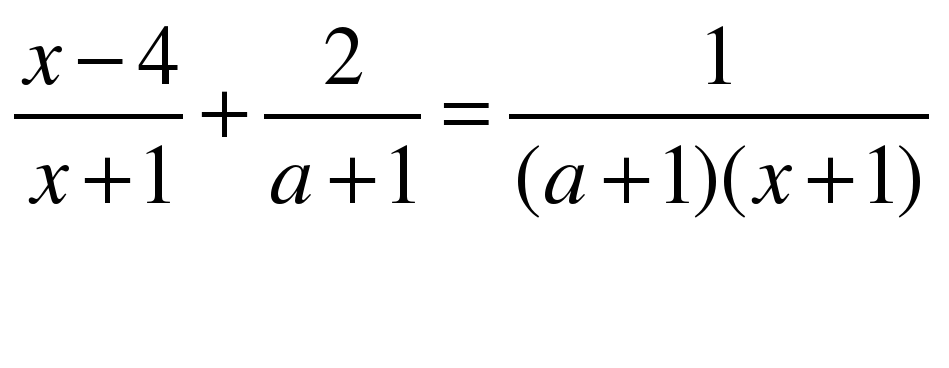
Самостоятельная работа №2
| Вариант №1 1. Найдите все значения параметра а, при каждом из которых система уравнений 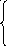 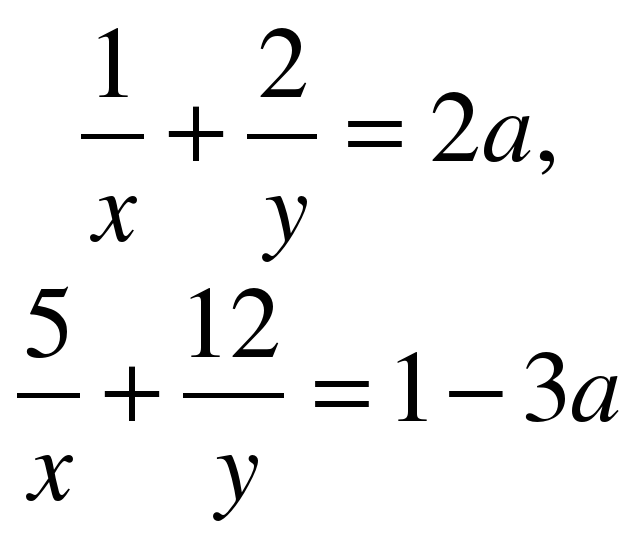 имеет хотя бы одно решение. имеет хотя бы одно решение. 2. При каждом значении параметра а решите неравенство  . . 3. Найдите все значения параметра а, при каждом из которых решением неравенства 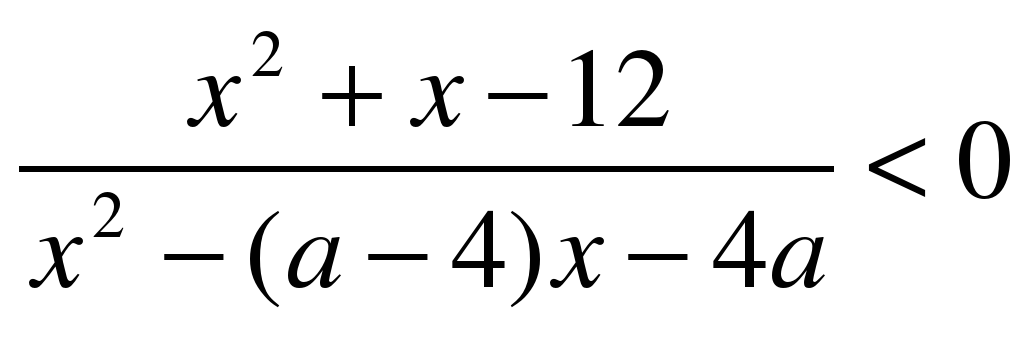 является объединение двух непересекающихся интервалов. является объединение двух непересекающихся интервалов.
|
Вариант №2 1. Найдите все значения параметра а, при каждом из которых система уравнений 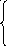  имеет хотя бы одно решение. имеет хотя бы одно решение. 2. При каждом значении параметра а решите неравенство  . . 3. Найдите все значения параметра а, при каждом из которых решением неравенства 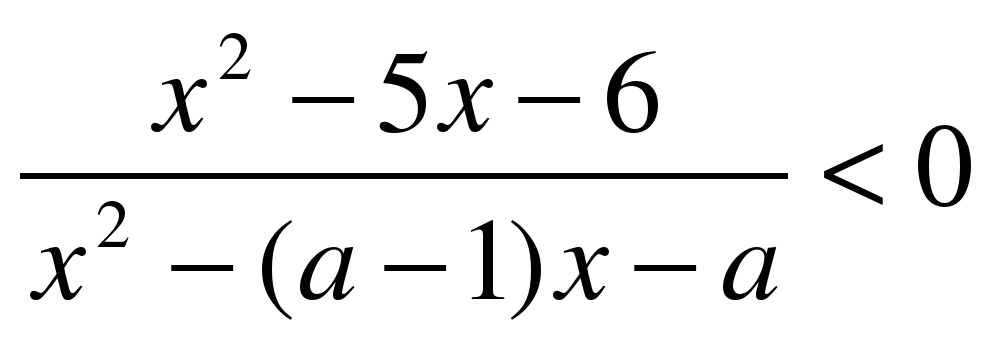 является объединение двух непересекающихся интервалов. является объединение двух непересекающихся интервалов. |
Самостоятельная работа №3.
|
Вариант №1 1. Найдите все значения параметра а, при каждом из которых решения уравнения 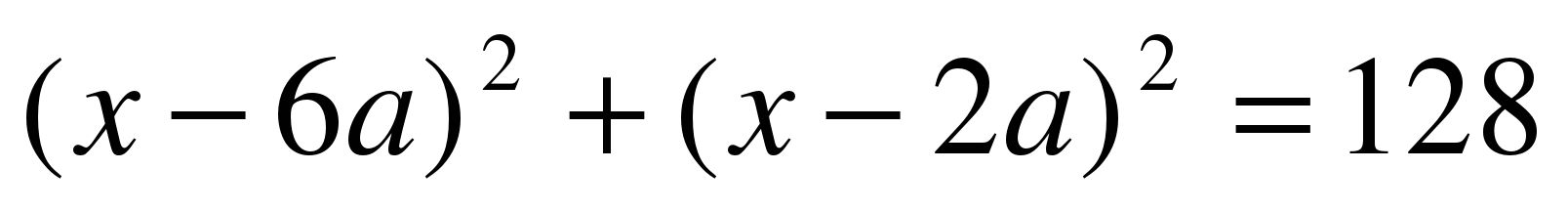 симметричны относительно точки симметричны относительно точки  . . 2. Для каждого значения параметра а найдите число решений уравнения 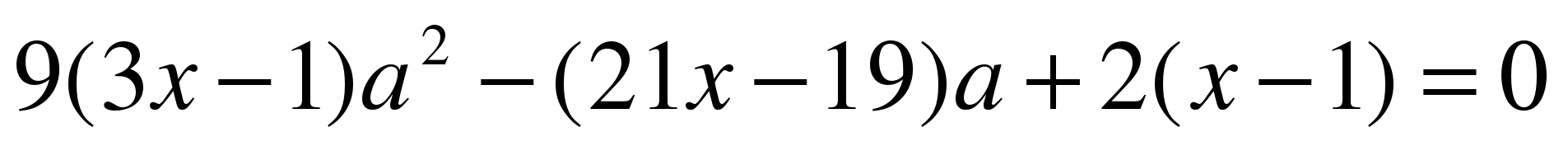 . . 3. Найдите все значения параметра а, при каждом из которых больший корень уравнения  в 6 раз больше, чем его меньший корень. в 6 раз больше, чем его меньший корень. 4. Найдите все значения параметра а, при каждом из которых уравнения  и и  имеют хотя бы один общий корень. имеют хотя бы один общий корень. 5. Определите, при каких значениях параметра а неравенство  верно для всех верно для всех 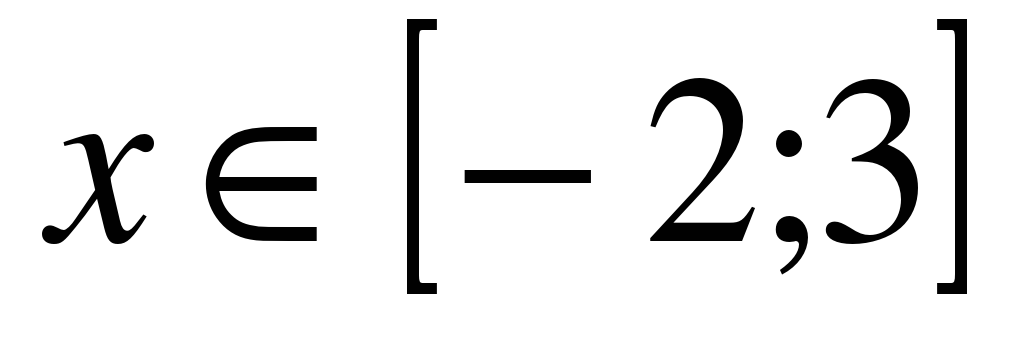 . .
|
Вариант №2 1. Найдите все значения параметра а, при каждом из которых решения уравнения 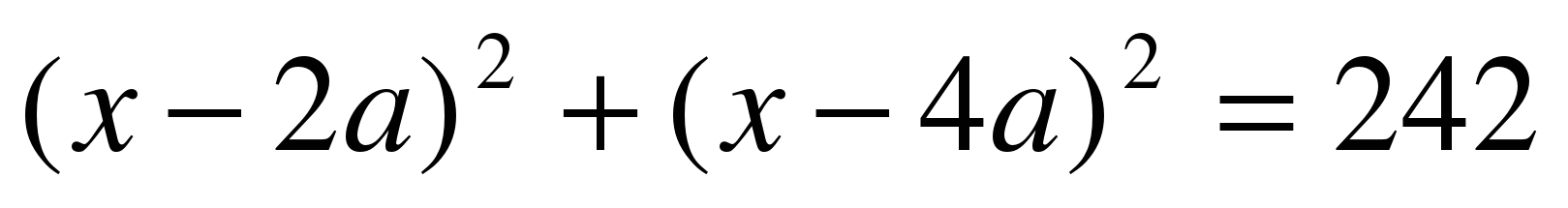 симметричны относительно точки симметричны относительно точки 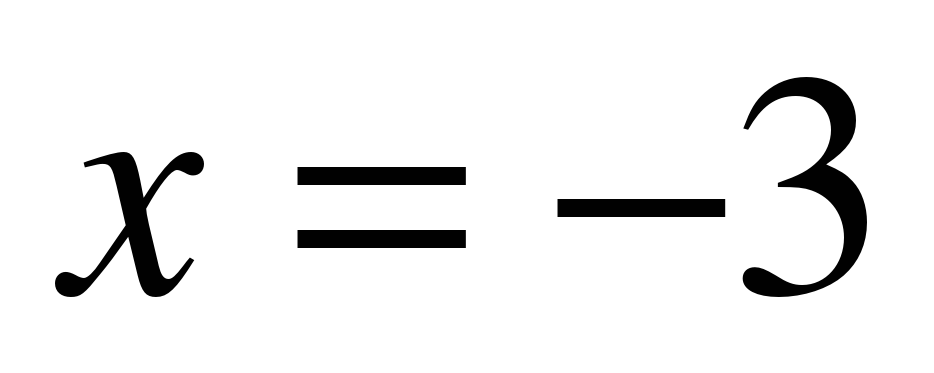 . . 2. Для каждого значения параметра а найдите число решений уравнения 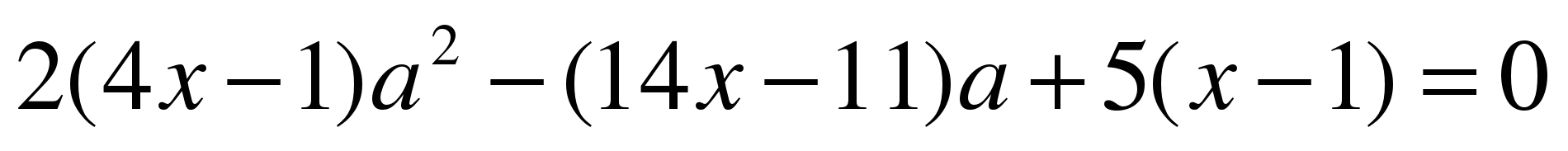 . . 3. Найдите все значения параметра а, при каждом из которых больший корень уравнения  в 10 раз больше, чем его меньший корень. в 10 раз больше, чем его меньший корень. 4. Найдите все значения параметра а, при каждом из которых уравнения  и и  имеют хотя бы один общий корень. имеют хотя бы один общий корень. 5. Определите, при каких значениях параметра а неравенство 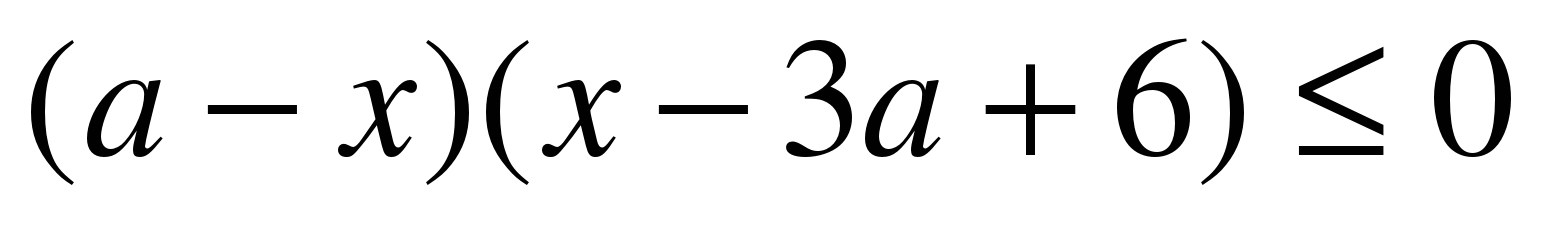 верно для всех верно для всех  . .
|
Методическое обеспечение темы «Решение уравнений и неравенств с модулем».
Самостоятельная работа№1 « Линейные уравнения и системы линейных уравнений с модулем»
| Вариант 1 | Вариант 2 |
׀׀х-2|-3| = 1 ׀х-2| + |х + 3| = 7 ||3х + 6| + 1| = 5 |х| + 3|х + 2| = 2|х+1| |5+х|-|8-х| = 13 ||х + 2| - |х -6׀׀= |х׀
׀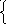 х-1| + |у-2| = 3, х-1| + |у-2| = 3, |x-l׀-׀у-2| = l
x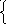 -׀у-4| = 4, -׀у-4| = 4, |x-3| + |у-4 ׀= 3.
| |4-Зх|-2 = 0 |х-5|-|х-2| = 3 3|х-1|-2|х-2| + |х + 3| = 2 ׀х + 3| + |х-3| = 6 ׀х-3| + |х-1| = 3 |2-|1-|х||| = 1.
3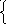 х-у = 3. х-у = 3. 2х + 3|у| = 13
|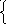 х + у׀ = 2, х + у׀ = 2, ׀х׀+׀у׀ = 3
|
Самостоятельная работа№2 «Квадратные уравнения с параметром»
| Вариант 1 | Вариант 2 |
х2-6|х|-2 = 0 |х + 3| = х2+х-6 |х2-4х-1|=х2 + 6х + 1 |х2-9| + |х-3| = 6. |х2 - 5х + 4| +|х2 - 5х + 6| = 2.
| х2 — 4|х| — 1=0 |х2 + х - 3| =х |Зх2+х-7| = Зх2-Зх-1 |х2-9| + ׀х-2׀=5 |х2-4х + 3|+|х2-5х + 6| = 1 |
Самостоятельная работа№3 «Линейные неравенства с модулем»
| Вариант 1 | Вариант 2 |
|2х-6| |3х- 1| |2х-5׀ |4х-1| + 2х-4 |2х-6| + |4-х|
| |4х-8׀ |4х+1| |2х-6׀ |3-х|-|х-2| |4х-8 + |4-х|׀ |
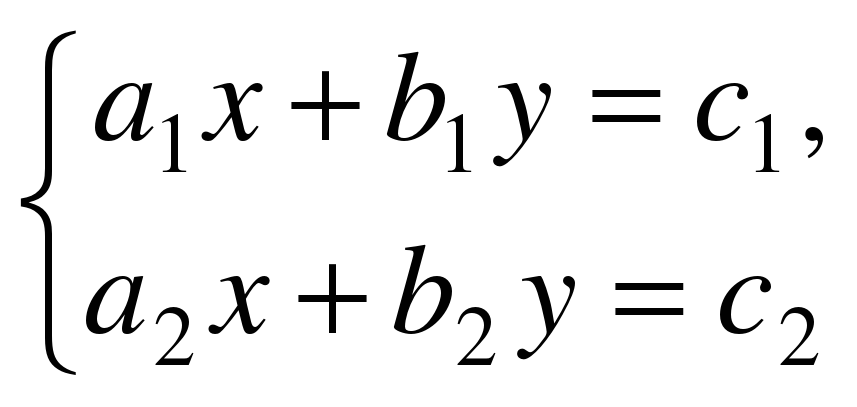 имеет единственное решение, если коэффициенты при неизвестных не пропорциональны. Условие пропорциональности удобно записать так:
имеет единственное решение, если коэффициенты при неизвестных не пропорциональны. Условие пропорциональности удобно записать так:  Б)
Б) 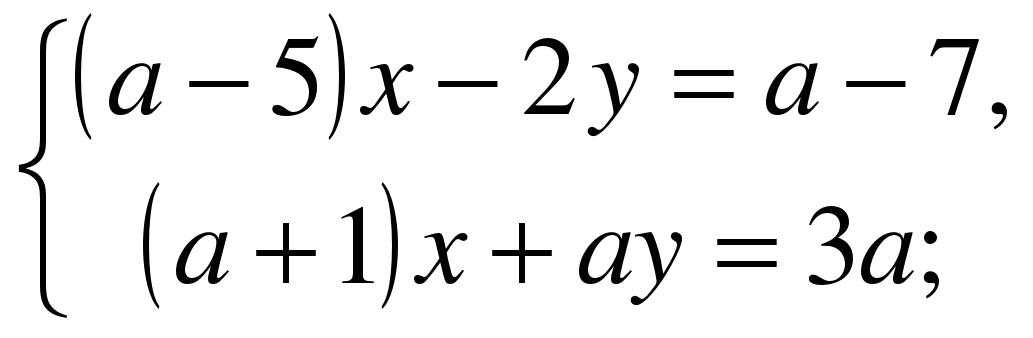
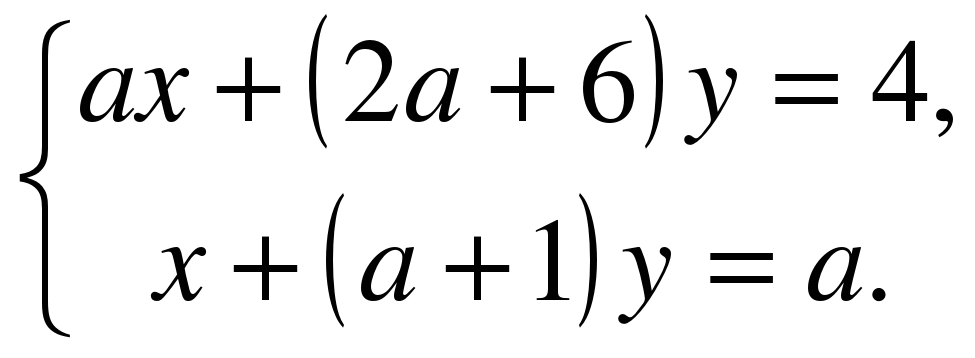

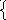 ) x
) x  ) х≥2
) х≥2 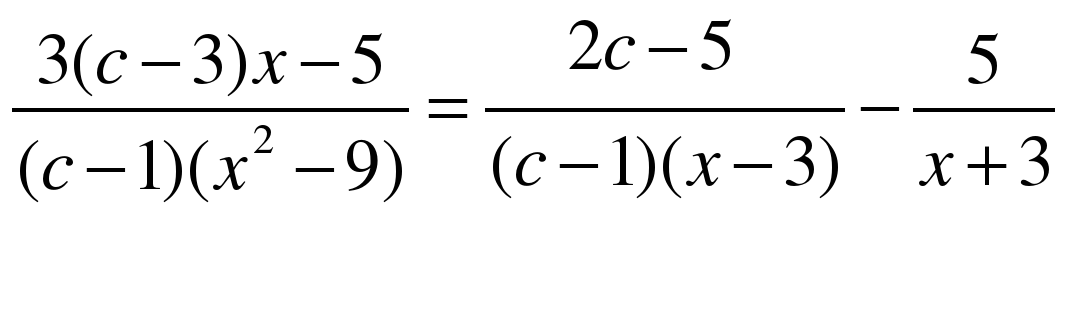
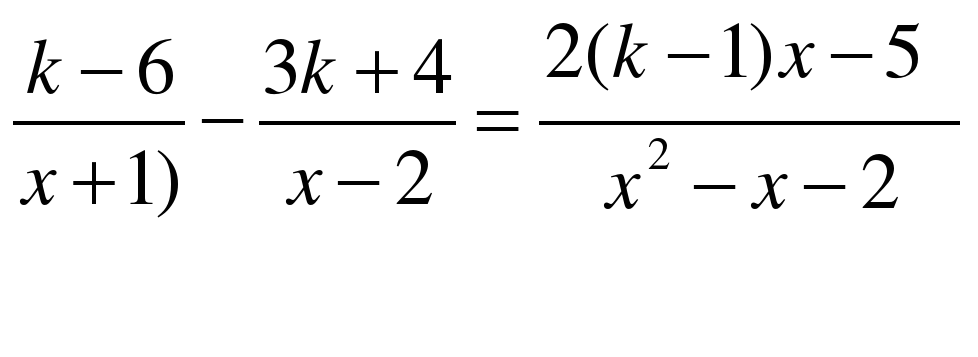
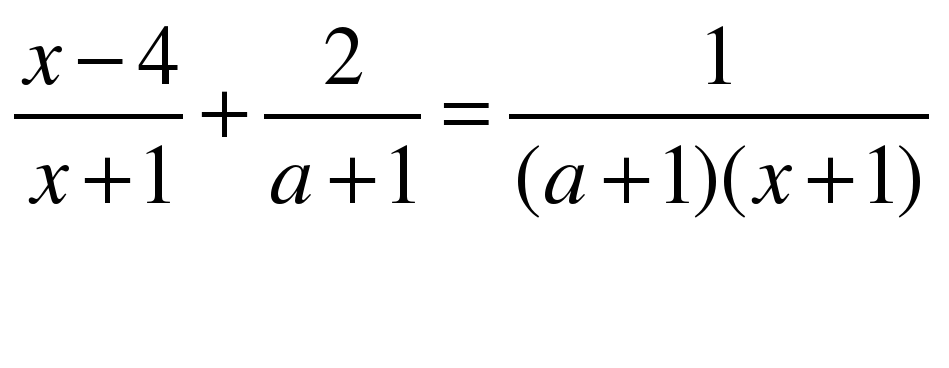
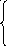
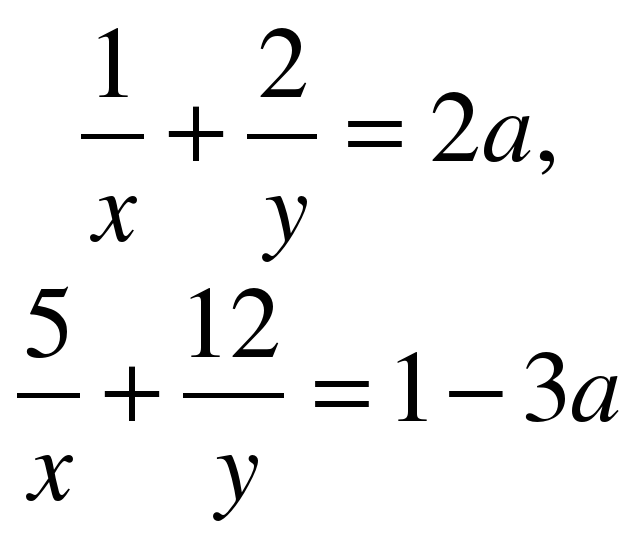 имеет хотя бы одно решение.
имеет хотя бы одно решение. имеет хотя бы одно решение.
имеет хотя бы одно решение.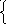 х-1| + |у-2| = 3,
х-1| + |у-2| = 3,















