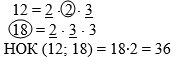Памятка № 1 Делители и кратные.
Делителемнатурального числаaназывают натуральное число b, на которое a делится без остатка.
Делители числа можно перечислить все. Самый маленький делитель числа – 1. Самый большой делитель числа – само число. Если a :b, то числоb – делитель числа a
Например: 1) Делители12: 1; 2; 3; 4; 6; 12, т.к. число 12 делится нацело на каждое из указанных чисел. 2) Делители 54: 1; 2; 3; 6; 9; 18; 27; 54. 3) Делители 61: 1; 61.
Кратнымнатурального числа aназывают натуральное число с, которое делится без остатка на a.
Кратных числа бесконечно много, перечислить все нельзя
Самое маленькоекратное числа–само число. Самого большого кратного не существует. Еслис :а, то числос – кратное числа a
Например: 1) Кратные 12: 12; 24; 36; 48; 60; …, т.к. каждое из указанных чисел делится нацело на 12.
2) Кратные 54: 54; 108; 162; … 3) Кратные 15: 15; 30; 45; 60; … | Памятка № 2 Признаки делимости
1) Если запись натурального числа оканчивается цифрой 0, то это число делится нацело на 10. Кратные 10: 20; 60; 80; 140; …, т.к. запись каждого числа оканчивается цифрой 0.
2)Если запись натурального числа оканчивается цифрой 0 или 5, то это число делится нацело на 5. Кратные 5: 15; 20; 45; 230; …, т.к. запись каждого числа оканчивается цифрой 0 или 5.
0, 2, 4, 6, 8 – чётные цифры | 1, 3, 5, 7, 9 – нечётные цифры |
3)Если запись натурального числа оканчивается чётной цифрой, то это число делится нацело на 2. Кратные 2: 4; 10; 32; 56; 98; …, т.к. запись каждого числа оканчивается чётной цифрой.
4) Если сумма цифр числа делится нацело на 3, то и само число делится нацело на 3. 582 – кратно 3, т.к. 5 + 8 + 2 = 15; 15 – делится нацело на 3. 6 708 – кратно 3, т.к. 6+7+0+8= 21; 21 – делится нацело на 3. 647– некратно 3, т.к. 6 + 4 + 7 = 17; 17 – не делится нацело на 3.
5) Если сумма цифр числа делится нацело на 9, то и само число делится нацело на 9. 162 – кратно 9, т.к. 1 + 6 + 2 = 9; 9 – делится нацело на 9. 5 382 – кратно 9, т.к. 5+3+8+2= 18; 18 – делится нацело на 9. 374– некратно 9, т.к. 3 + 7 + 4 = 14; 14 – не делится нацело на 9.
6)Если запись натурального числа оканчивается чётной цифрой и сумма цифр числа делится нацело на 3, то это число делится нацело на 6. 582 – кратно 6, т.к. 5 + 8 + 2 = 15; 15 – делится нацело на 3, запись числа оканчивается чётной цифрой. |
Памятка № 3 Простые и составные числа
Натуральное число называется простым, если оно имеет только два делителя: 1 и само это число Например, 23 – простое число, т.к. делится нацело на 1 и на 23
Число 2 – наименьшее простое число. Простых чисел бесконечно много, поэтому наибольшего простого числа нет. Таблица простых чисел на 1 форзаце учебника.
Натуральное число называется составным, если оно имеет более двух делителей.
Например, 12 – составное число, т.к. имеет более двух делителей: делится нацело на 1; 2; 3; 4; 6; 12.
Число 4 – наименьшее составное число. Составных чисел бесконечно много, наибольшего составного числа нет.
Разложение на простые множители
Любое составное число можно представить в виде произведения простых множителей, т.е. разложить на простые множители.
1 способ | 2 способ | Разложить число 330 на простые множители 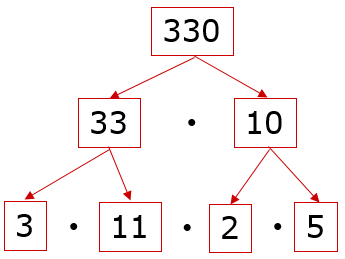 330 = 2 ∙ 3 ∙ 5 ∙ 11 | Разложить число 162 на простые множители

162 = 2 ∙ 3 ∙ 3 ∙ 3 ∙ 3 = 2 ∙ �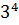 � � |
Произведение одинаковых множителей заменяют степенью, множители располагают в порядке возрастания. | 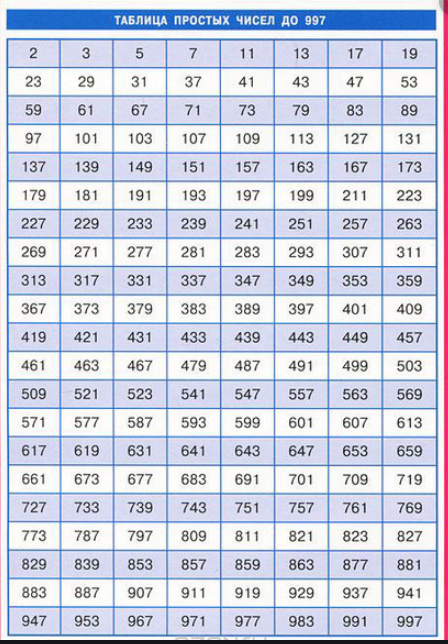
|
М – 6 Памятка № 4 Наибольший общий делитель (НОД)
Наибольшее натуральное число, на которое делится нацело каждое из двух данных чисел, называют наибольшим общим делителем этих чисел. 1 способ Делители 18:1; 2; 3; 6; 9; 18. Делители 45:1; 3; 5; 9; 15; 45. НОД(18; 45) = 9. | 1) Выписать все делители каждого числа 2) Подчеркнуть все общие делители. 3) Выбрать из общих делителей наибольший | 2 способ 12 = 2· 2 · 3 18 = 2 · 3 · 3 НОД (12; 18) = 2 · 3 = 6
| 1) Разложить каждое из чисел на простые множители. 2) Подчеркнуть все одинаковые простые множители. 3) Найти произведение подчеркнутых в одном числе множителей. 4) Записать результат. | Если у чисел нет одинаковых простых множителей, то НОД равен 1. Например, НОД(12; 35) = 1.
Если наибольший общий делитель двух натуральных чисел равен 1,то числа называют взаимно простыми. Например, НОД(4; 17) = 1, то 4 и 17 – взаимно простые числа
Любые два простых числа являютсявзаимно простыми. Например, НОД(3; 19) = 1, т.к.3 и 19 –простые числа
Если большее число делится нацело на меньшее, то НОД равен меньшему числу. Например, НОД(24; 8) = 8, т.к. 24 делится нацелона 8. Например, НОД(53; 106) = 53, т.к. 106 делится нацелона 53. | М – 6 Памятка № 5
Наименьшее общее кратное (НОК)
Наименьшее натуральное число, которое делится нацело на каждое из двух данных чисел, называют наименьшим общим кратным этих чисел 1 способ Кратные 12:12; 24; 36; 48; 60; 72;... Кратные8:8; 16; 24; 32; 40; 48; 56; 64; 72;... НОК(12; 8) = 24. | 1) Выписать несколько первых кратных каждого числа 2) Подчеркнуть все общие кратные. 3) Выбрать из общих кратных наименьшее | 2 способ 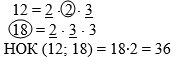 | 1) разложить каждое из чисел на простые множители; 2) подчеркнуть одинаковые простые множители; 3) обвести в кружок самое большое из данных чисел; 4) обвести в кружок те простые множители, которые не подчеркнули в разложении меньшего числа; 5) умножить числа, обведенные в кружок. | Если у чисел нет одинаковых простых множителей, то НОК равнопроизведению данных чисел. Например, 12 = 2 ∙2 ∙ 3 35 = 5∙7
| НОК(12; 35) = 12 ∙ 35 = 420.
| Если большее число делится нацело на меньшее, то НОК равнобольшему числу. Например, НОК(24; 8) = 24, т.к. 24 делится нацелона 8. Например, НОК(53; 106) = 106, т.к. 106 делится нацелона 53.
|