Интеграция предметов естественнонаучного цикла в преподавании математики, как средство развития функциональной грамотности школьника.
Кравченко НИ.
Карагугинская средняя школа район М. Жумабаева Северо-Казахстанская область
В Послании Президента РК Н.А.Назарбаева народу Казахстана «Стратегия «Казахстан-2050» Новый политический курс состоявшегося государства» большое внимание уделяется вопросам сферы образования. «Чтобы стать развитым конкурентоспособным государством, мы должны стать высокообразованной нацией» отмечено в Послании.
Для повышения конкурентоспособности образования, развития человеческого капитала путем обеспечения доступности качественного образования, тем самым обеспечивая устойчивый рост экономики нашей республики – была разработана Государственная Программа развития образования Республики Казахстан на 2011-2020 годы. Одним из программных целей программы является «формирование в общеобразовательных школах интеллектуального, физически и духовно развитого гражданина Республики Казахстан, удовлетворение его потребности в получении образования, обеспечивающего успех в быстро меняющемся мире, развитие конкурентоспособного человеческого капитала для экономического благополучия страны».
Внедрение современных методов и технологии, повышения качества образования является гарантией развития Казахстана.
Обществу необходим человек функционально грамотный, умеющий работать на результат, способный к определенным, социально значимым достижениям.
Функциональная грамотность учащихся - это определенный уровень образованности учащихся на уровне общего среднего образования, выражающий степень овладения учащимися ключевыми компетенциями, позволяющий эффективно действовать в учебной деятельности и за ее пределами.
В общеобразовательной школе предметы естественнонаучного цикла изучаются только в пределах обязательного минимума. Однако эти предметы призваны раскрыть перед учащимся современную научную картину мира. Знания о природе составляют естественнонаучный фундамент мировоззрения современного человека. Значит, каждый момент получения знаний должен быть одновременно и формированием целостности сознания учащегося, единой системы знаний о природе – интегрального ее образа.
При постижении великой правды природы, учащиеся ощущают объемность недостаточно систематизированных знаний о ней. Решить эту проблему позволяет интеграция предметов. Одной из форм реализации интегрированного подхода к обучению является установление межпредметных связей на уроках естественного цикла. Они играют важную роль в повышении практической и научно-теоретической подготовке учащихся, существенной особенностью которой является овладение школьниками обобщенным характером познавательной деятельности.
Интегрированный характер получаемых знаний дает возможность применять их в конкретных ситуациях, при рассмотрении частных вопросов, как в учебной, так и во внеурочной деятельности.
Интеграция – это не самоцель, а определённая система в деятельности учителя, она должна решать определённые задачи интегрированного обучения:
– повышать уровень знаний учащихся по предмету, который проявляется в глубине усваиваемых понятий, закономерностей за счёт их многогранной интерпретации с использованием сведений интегрируемых наук;
– изменять уровень интеллектуальной деятельности, путём рассмотрения учебного материала с позиции ведущих идей, установлением естественных взаимосвязей между изучаемыми проблемами;
– повышать познавательный интерес учащихся, проявляемый в желании активной и самостоятельной работы на уроке и во внеурочное время;
– включать учащихся в творческую деятельность.
Интеграция необходима в современной системе образования. Во-первых, традиционная «монологическая» система в образовании почти полностью утратила свою практическую эффективность. Во-вторых, в современной школе учебные дисциплины носят «конкурирующий» характер. Каждая противостоит всем остальным, как бы претендуя на большую значимость по сравнению с другими. В-третьих, каждая из школьных дисциплин сама по себе представляет набор сведений из определенной области знаний, поэтому не может претендовать на тесное взаимодействие, при сохранении предметного «лица».
Интеграция в современной школе идет по нескольким направлениям и на разных уровнях. Эти уровни: внутрипредметный и межпредметный. Внутрипредметная интеграция включает фрагментарную интеграцию, с отдельными фрагментами урока, требующими знаний из других предметов, узловую интеграцию, когда на протяжении всего урока учитель опирается на знания из других предметов, что составляет необходимое условие усвоения нового материала. Особое внимание заслуживает понятие величины, которое используется во многих науках, но для курсов физики и математики является наиболее характерным. Величины, изучаемых в школе отражают многочисленные свойства реального мира. В поле зрения учителя математики, физики должны быть вопросы согласования терминологии, обозначений систем е единиц измерения, содержания приводимых примеров и иллюстраций различных величин (длина, ширина, расстояние, мера угла и дуги, площадь, объём, масса, вес, сила). Немаловажное значение имеет согласованное формирование понятий вектора, векторной величины на уроках физики и математики.
Для стыковки преподавания предметов естественно-математического цикла существенное значение имеет то, как школьники овладевают навыками приближённых вычислений. Выработка единых требований к выполнению действий с приближёнными числами при измерениях величин – важное звено в совместной деятельности учителя математики, химии, физики , трудового обучения.
Одним из элементов связи математики и физики является понятие функции. Физика снабжает математику многочисленными примерами различных видов функций. Эти примеры должны использоваться в работе по формированию функциональных понятий на уроках математики. С другой стороны, навыки работы с функциональным материалом находят применение в решении конкретных физических задач. На уроках математики должны найти подобающее место задания, в которых необходимо определить значение конкретной физической величины при заданных значениях параметров входящих в данную формулу; выразить одну переменную через другие; изобразить схематически график функции, заданной физической формулой, и т. п. Приведем примеры таких заданий.
1) В следующих формулах выразите каждую переменную через другие:
a) m = ρV; б) s=υt; в) Q = cm(t-t0);
2. Даны функции:
а) s=at2 /2 где а — const;
б) Ек =mv2/2 , где v — const;
в) Q = I2Rt, где R—-const и t — const.
Укажите, какие из них являются функциями вида y=k x , у = ах2.
3. Сопротивление f дороги движению автомобиля при скорости движения v км/ч выражается следующими формулами:
а) на асфальте f=14,5+0,25 v;
б) на хорошем шоссе f=24- 2/3 v + 1/30 v2
в) на булыжной мостовой f=29 - 2/3 v +1/16 v2
г) на мягкой грунтовой дороге f=36,5-3/4 v +1/30 v2
Определите для тех случаев, когда это возможно, скорость, при которой сопротивление будет наименьшим.
Особое место в физике и математике занимает тема « Производная».
Примеры некоторых задач.
1. Материальная точка движется прямолинейно по закону x(t)=t3- 4t2. Найдите скорость и ускорение в момент времени t=3с.
2. При торможении маховик за время t где x(t) – координата точки. В какой момент времени скорость точки будет поворачивается на угол. Найдите угловую скорость вращения маховика в момент времени t = 2
3. Точка движется по координатной прямой согласно закону, равна 6? Найти ускорение точки в этот момент времени.
4. Найдите силу F (F=ma), действующую на материальную точку с массой m, движущуюся прямолинейно по закону
5. Тело движется прямолинейно в вертикальном направлении (t -время движения, h- расстояние от поверхности земли до тела). Определить начальную скорость движения
6. Тело массой 2кг движется прямолинейно по закону. Координата х измеряется в сантиметрах, время t – в секундах. Найдите кинетическую энергию Е тела через 2с после начала движения.
Для достижения связей математики и черчения необходимо добиваться от учащихся прочного навыка выполнения основных геометрических построений: построение параллельных прямых, равных углов, проведение перпендикуляра к прямой, деление отрезков и углов на равные части и. т. д. На уроках черчения эти навыки получают дальнейшее развитие при делении окружности на 5, 6 частей, что, в свою очередь, может использоваться на уроках геометрии по теме: «Правильные многоугольники». Основы методов, которыми оперирует черчение, закладывается в геометрии. Наиболее глубокие связи в содержании в методах между черчением и геометрией раскрываются при изучении вопросов параллельного проектирования и изображении фигур в стереометрии. Здесь уместно использовать сведения о косоугольных проекциях, с которыми учащиеся познакомились на уроках черчения.
Для успешного применения математических знаний по химии учащиеся должны свободно владеть записью числа в стандартном виде и действия с этими числами, процентными вычислениями, навыками составления пропорций, уравнений, чтения графиков ит.п. При изучении соответствующих тем курса математики и при последующем повторении полезно предлагать учащимся задания химического содержания, например: выполнить вычисления по химической формуле, записать в стандартном виде молекулярную массу кислорода, водорода и т. д., сравнить атомные массы ряда веществ, определить процентную концентрацию вещества в растворе, найти массу продукта реакции по известному количеству вступающих в реакцию веществ и т. п.
Примеры химических задач.
1.Морская вода содержит 5 % соли. Сколько пресной воды нужно добавить к 80 кг. Морской воды , чтобы концентрация соли составила 4 %.
2.Имеется 0,5 т. целлюлозной массы, содержащей 85 % воды. Сколько килограммов воды надо выпарить, чтобы оставшаяся масса содержала 25 % воды?
3. Смесь, состоящая из двух веществ, весит18 кг. После того , как из неё выделили 40 % первого вещества и 25 % второго, в ней первого вещества осталось столько же, сколько и второго. Сколько каждого вещества было в смеси ?
4. В растворе содержится 40 % соли. Если добавить 120 г. Соли , то в растворе будет содержаться 70 % соли. Найдите массу соли в первоначальном растворе.
При отработке навыков чтения графиков полезно использовать конкретный материал из курса химии, например кривые растворимости соли, графики зависимости температуры плавления и кипения вещества от количественного состава предельных углеводородов.
Элементы математики привлекаются и на уроках географии, в частности в вопросах масштабных соотношений, преобразование подобия. При изучении соответствующего материала на уроках математики необходимо предлагать учащимся задания на нахождение расстояний между пунктами по карте. Эти умения используются в соревнованиях по спортивному ориентированию.
Большое впечатление на учащихся оказывает выявление связи математики с биологией. Эту связь целесообразно раскрывать в разных темах курса. Но особенно много возможностей имеется в старших классах. Например, вызывает искреннее удивление учащихся настоящие конструкторские шедевры - созданные пчёлами соты. Они состоят из ряда шестигранных восковых ячеек. В пределах рамки сотов это самая плотная упаковка, позволяющая, во-первых, наивыгоднейшим образом, разместить в ячейки личинку и, во-вторых, при максимально возможном объеме наиболее экономным образом использовать строительный материал - воск.
И
нтересно наблюдать расположение листьев на стебле. Они располагаются не по прямой, а окружают ветку по спирали так, чтобы, не мешая друг другу, воспринимать солнечный свет. Сумма предыдущих шагов спирали, начиная с вершины, равна величине последующего шага, т.е. А+В=С В+С=Д и т.д. Расположение семянок в головке подсолнуха или листьев на побегах вьющихся растений соответствует логарифмической спирали
Очень интересны и поучительны задачи экологического содержания.
1.Одно растение василька производит в среднем 1500 семян. Семена сохраняют всхожесть до 10 лет. Определите запасы семян этого сорняка в почве после5 лет засорения им посевов на одном поле.
2. В одной коробочке мака до 3000 семян Таких коробочек на растении до 10. Всхожесть семян до 10 лет. Подсчитайте потомство одного растения за 3 года.
3.В одном колосе пшеницы до 45 зерен . Всхожесть сохраняется до 32 лет . Подсчитайте урожай пшеницы за 7 лет.
4.Гидра размножается почкованием, при чём, при каждом делении получается 5 новых особей. Сколько особей будет после восьми делений? Какое количество делений необходимо для получения 625 особей?
5.Плодовитость дальневосточной горбуши 1,5 тыс. икринок. В гнезда попадают только 58 % икры, содержащейся в самке , остальная часть сносится течением. До весны сохраняется всего 4% икринок. Мальки выносятся течением в море, устья реки достигают не более 1,8% мальков. Через несколько лет взрослая горбуша возвращается из моря в реку, где она родилась, и приступает к размножению, после которого погибает. В среднем до половозрелого состояния доживает одна особь из 750 зародышей. Постройте кривую выживания потомства дальневосточной горбуши.
6.Осетр живёт 50 лет. Каждый год он мечет 300 тыс. икринок, выметывая за свою жизнь более15 млн. Подсчитайте потенциально возможное потомство 3 самок за 10лет.
Эти задачи можно использовать при прохождении прогрессии.
Математическое образование играет важную роль, как в практической, так и в духовной жизни общества. Практическая сторона математического образования связана с формированием способов деятельности, духовная – с интеллектуальным развитием человека, формированием характера и общей культуры человека.
Учащимся предлагается самостоятельно понаблюдать отдельные сельскохозяйственные работы (а может быть и принять в них участие): сбор хлопчатника, съемка плана участка, отводимого под какую-либо культуру, расчет количества требуемых удобрений, разметка участка под посадку сада и др. В результате наблюдений школьники должны выявить задачи, с которыми приходится встречаться агроному, механизатору, садоводу и т. д. Эти задачи учащиеся должны четко сформулировать, решить и представить для дальнейшего обсуждения всего класса. Укажем отдельные задачи:
1. Самоходная косилка КС-10 имеет ширину захвата 10 м и движется со скоростью 4,5 км/ч. Сколько гектаров можно выкосить ею за 10 ч, если затраты времени на повороты и остановки составляют 12% рабочего времени?
2. Кипа хлопка весит 190 кг, а ее размер 98·62·73 см. Найдите массу 1 м3 спрессованного хлопка.
3. Поле имеет форму прямоугольника с основанием 250 м и высотой 100 м. Через поле под прямым углом к основанию проходит проселочная дорога шириной 5 м. Найдите посевную площадь поля.
4. Объем сена, сложенного в стог, можно определить по следующей по приближенной формуле: V=lC / 72, где l — длина перекидки (рис. I), С — длина окружности стога на уровне груди человека. Вычислите, сколько сена в стоге, если l=15м, С = 20 м, а масса 1 м3 сена 50 кг. Выполнив необходимые измерения, вычислите массу одного стога сена в вашем подсобном хозяйстве
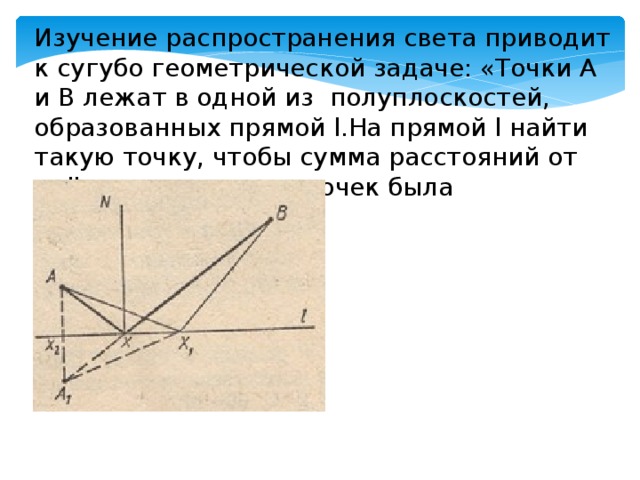
5. Для снабжения водой двух селений А и В, расположенных по одну сторону канала (рис. 2), требуется построить на берегу канала водонапорную башню. Где ее нужно расположить, чтобы она была на равных расстояниях от А и от В?
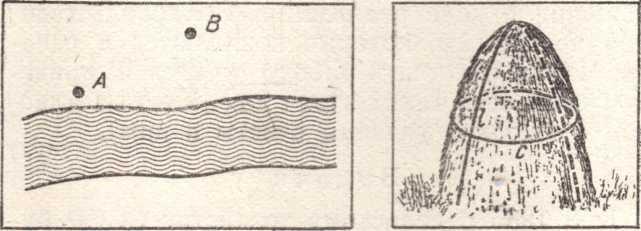
Рис. 2 Рис. 1
6. На полевом стане требуется установить фонарь так, чтобы он одинаково освещал три объекта, не лежащие на одной прямой. Как выбрать место установки фонаря?
7. Пруд имеет форму квадрата. В вершинах его растут 4 дерева. Как можно увеличить вдвое площадь пруда, сохранив его форму, не уничтожая и не затопляя деревья?
8. С участка кукурузы, имеющего форму трапеции с основаниями 280 и 320 м и высотой 180 м, собрано зеленой массы в среднем по 150 ц с гектара. Сколько рейсов должна сделать грузовая машина ЗИЛ-150 для доставки кукурузы в силосную башню, если ее грузоподъемность 2 т, а коэффициент использования грузоподъемности для данного груза равен 0,75?
9. Два комбайнера должны убрать поле прямоугольной формы размером 800·600 м. Уборку начал первый комбайнер с края поля, двигаясь параллельно его большей стороне с постепенным приближением к центру поля. На каком расстоянии от края, с которого началась уборка, второй комбайнер должен заменить первого, чтобы первый смог собрать урожай с 2/3 площади всего поля.
В практической направленности обучения существенная роль принадлежит геометрии. Именно на уроках по этому предмету дети учатся измерять элементы сложных фигур, решать задачи на построение, моделировать и конструировать. Таким образом, они приобретают умения и навыки, являющиеся базовыми для многих видов трудовой деятельности. Конструирование: моделей треугольников к четырехугольников, шарнирных моделей, палеток, центроискателей. Разметка земельного участка под посадку плодовых деревьев. Изготовление разверток для конструирования моделей призм.
Указанные умения и навыки определяются школьными программами. Но отрабатывать их целесообразно не только на уроках, но и во время экскурсий или лабораторных работ. Важно подчеркнуть общедидактическое значение лабораторно-практических работ: при их выполнении протекает в органическом единстве развитие мышления, речи и практических умений учащихся.
На уроках математики нужно обеспечивать органическую связь изучаемого теоретического и задачного материала, формировать у учащихся прочные и осознанные математические навыки, необходимые как для дальнейшего изучения математики, так и для решения прикладных задач. Важное значение в процессе обучения математике имеет понимание школьниками практической значимости того или иного учебного материала, ближней и дальней перспективы его использования
Задачи практического содержания
1.Между электрическим столбом и зданием натянут кабель. Расстояние между зданием и столбом равно 10 метров, высота столба 8 м, а высота здания 4 м. Найдите длину электрического кабеля.
2.Из свинцового шара радиуса 10 мм делают цилиндрический диск толщиной 3 мм. Каков диаметр диска?
3.Сколько квадратных метров жести пойдёт на изготовление водосточной трубы длиной 6м и диаметром 22см, если швы прибавляют 3 % площади поверхности трубы?
4. Нужно сделать ремонт в комнате с высотой 2,5 м, шириной 5 м и длиной 6 м. Найти площадь поверхности стен.
Сколько рулонов обоев понадобится для оклейки стен, если ширина одного рулона 60 см, длина 10м.
Сколько при этом понадобится денег, если стоимость одного рулона 800 тенге, а одна пачка клея стоит 300 тенге. И ее расход 10 м2.
Сколько % отходов обоев при этом получится?
В комнате имеются две двери 2 и три окна размерами 1,4 . Вычислите площадь стен без окон и дверей, если размеры комнаты: высота 2,5 м, ширина 5 м, длина 6 м.
Сколько потребуется рулонов обоев для оклейки данной комнаты , если обои размерами 0,6·10 м..
Каковы затраты если цена одного рулона 800 тенге, а цена пачки клея 300 тенге. Расход 10м2.
Сколько % отходов обоев при этом получится?
Задачи экономического содержания
1.При цене билета на футбольный матч в 450 р. на стадион вместимостью 40 тысяч человек пришло 5 тысяч зрителей. При снижении цены билета до 200 р. На матч с участием тех же команд число болельщиков, решивших посетить матч. Увеличилось до 30 тыс. человек. На основе анализа статистических данных было установлено. Что спрос на билеты задается линейной функцией. Определите, какую цену на билет должна установить администрация стадиона, чтобы во время игры данных команд стадион был заполнен полностью.
2. На валютном рынке сложилась следующая ситуация : при курсе 10 р./долл. Объём рыночного предложения валюты равен нулю, а величина спроса составляет 60 мл. дол. Кроме того, известно, что при курсе 30 р./дол. Рынок находится в равновесии и равновесный объём продаж валюты составляет 40 мл. долл. Исследования финансовых аналитиков показали ,что зависимости величины спроса и объёма предложения валюты от её цены характеризуются линейными функциями. Определите, какой объём валюты должен продать или купить Центральный банк, чтобы снизить равновесный курс до 25 р./долл.?
4.Хватит ли 8500м2 изоляционной ленты для двукратного покрытия ею километра газопровода диаметром 1420мм?
5.Конусообразная палатка высотой 4м с диаметром основания 6м покрыта парусиной. Сколько квадратных метров парусины пошло на палатку?
6. Сколько краски потребуется для покрытия фронтона дома с двух сторон? Крыша двускатная. Ширина дома 12 м., расстояние от конька крыши до кирпичной кладки стен 2 м. Расход краски на 1 кв. м. 300 грамм.
7.Угольный пласт обычно залегает так, что его верхняя граница (конечно в грубом приближении) представляет собой часть плоскости. Какое наименьшее число скважин следует пробурить, чтобы определить, как расположен пласт?
8.Одному ученику в столовой на завтрак дают 20г сливочного масла. В школе 320 учеников. Сколько молока должно быть надоено на ферме, чтобы получить нужное количество масла? Молоко даёт 25% сливок, сливки дают 20% масла.
9. По итогам работы за год фирма получила 16 млн тг прибыли. Правление фирмы решило выделить на выплату дивидендов акционерам 25% от прибыли. Известно, что акционеры владели 8 000 акций стоимостью 1000тг каждая. Какую сумму дивидендов получит на каждую акцию акционер фирмы?
Следующий уровень – межпредметная или синтезированная интеграция, которая объединяет знания разных наук для раскрытия того или иного вопроса. На перекрестке этих подходов могут быть и разные результаты: рождение абсолютно новых предметов; рождение новых специальных курсов, обновляющих содержание внутри одного или нескольких смежных предметов; рождение блоков уроков, объединяющих материал одного или ряда предметов с сохранением их независимого существования;
разовые интегрированные уроки разного уровня и характера. Интегрированные уроки снимают утомляемость и перенапряжение учащихся за счет переключения с одного вида деятельности на другой. Например « Симметрия», «Десятичные дроби», «Правильные многоугольники», «Многогранники» можно провести совместно с уроками физики, химии, биологии, черчения, технологии, так как они содержаться в той или иной мере в каждом из этих предметов и дают образное и целостное представление об окружающем нас мире. Так тема распространение света с математикой казалось бы не имеет общего, сводится решению геометрической задачи.
Знаете ли вы, что общего между заходом Солнца и функцией синус?
Исходя из наблюдаемой картины движения Солнца по небесной сфере и описания зависимости момента захода Солнца от даты календаря.
Для восточных земель ФРГ. Возобновление занятий в школе после летних каникул метеорологически совпадает со временем, когда день, т. е. период, когда Солнце находится над горизонтом, уменьшается с 16 и более часов во время летнего солнцестояния до 13,5 часов (на широте Берлина), а к концу сентября день становится короче ночи.
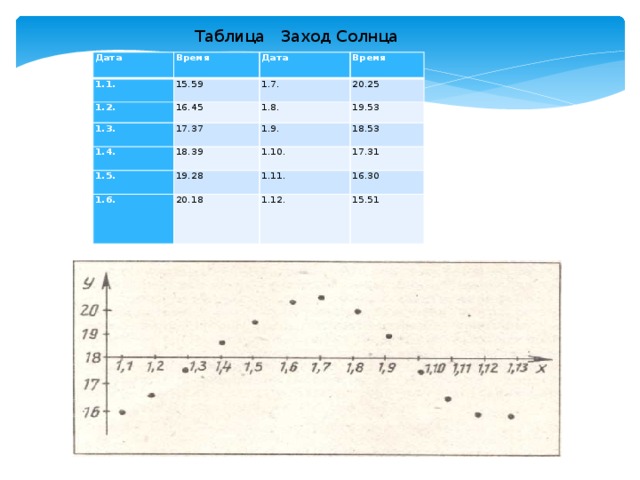
С помощью отрывного календаря нетрудно отметить момент захода Солнца на 1-е число каждого месяца (см. таблицу) и, соединив полученные точки плавной линией, построить график, взяв в качестве оси абсцисс среднее время захода Солнца — 18 ч (см. рисунок).
При более подробном рассмотрении графика создается впечатление, что множество точек расположено вдоль вол новой линии; школьники довольно быстро
Таблица
Заход Солнца
| Дата | Время | Дата | Время |
| 1.1. | 15.59 | 1.7. | 20.25 |
| 1.2. | 16.45 | 1.8. | 19.53 |
| 1.3. | 17.37 | 1.9. | 18.53 |
| 1.4. | 18.39 | 1.10. | 17.31 |
| 1.5. | 19.28 | 1.11. | 16.30 |
| 1.6. | 20.18 | 1.12. | 15.51 |
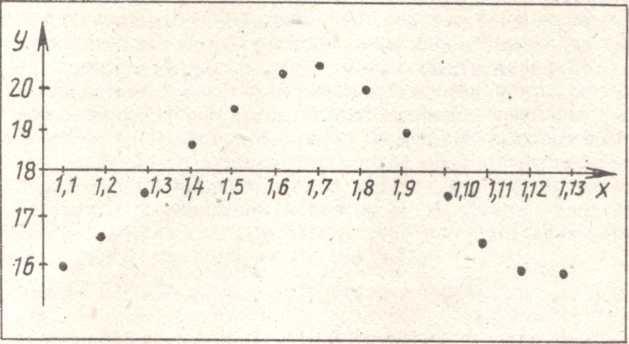
замечают возможность уточнения этой линии — если нанести на график еще по 15 (или даже по 30) точек в течение каждого месяца, считая месяц округленно за 30 дней. Можно также изготовить аналогичную таблицу (и график) для моментов восхода Солнца. Школьники вспоминают, что аналогичные графики они уже получали, изучая в курсе физики взаимосвязь кругового движения с изменением напряжения в генераторе переменного тока.
В ходе дальнейшей беседы учитель приводит еще ряд примеров, включая механические колебания, движения при плавании, движение ползущей змеи и т. п., а также указывает на аналогичные движения планет, хотя непосредственное наблюдение их движения в течение человеческой жизни не всегда достаточно наглядно. Аналогии со свойствами функций. Наш опыт показывает, что описанный путь может быть использован как для повторения определения функции и ее основных свойств, так и для обсуждения особенностей функций y=sin х и у=а sin х.
Не следует, разумеется, умалчивать о краевых условиях и границах применения этой модели. Так, некоторая сплющенность земного шара вдоль полярной оси приводит к некоторым отклонениям от «идеального» графика синуса. Кроме того, как мне указали сотрудники нашей обсерватории, отклонения вызываются и неравномерностью движения Земли, (по эллиптической, а не по круговой орбите), и соответственно некоторыми изменениями продолжительности «шага» таблицы, т. е. рассматриваемой единицы времени «1 календарный день» при введенном дискретном определении значений функции.
Эти два упрощения — сплющенность Земли и неравномерность ее движения — весьма незначительно искажают наш график; построение же дискретных точек графика является скорее преимуществом описанного метода
Каждому дню соответствует ровно один момент захода Солнца; день, когда Солнце не заходит, «запрещен» (не существует)
Область определения. Солнечная система существует если не вечно, то достаточно долго, как в прошлом, так и в будущем. Поэтому некоторые школьники утверждают, что область определения этой функции (-∞ , ∞), и мы не считаем это грубой ошибкой. Наименьший период. Легко видеть, что по истечении года все моменты захода Солнца повторяются в той же последовательности. Причина этих повторений — полный оборот Земли вокруг Солнца за год, считаемый для простоты за 365 дней; рассмотрение високосного года чрезвычайно усложняет расчеты. Таким образом, если известно, когда зашло Солнце 15 апреля такого-то года, можно быть уверенным, что 15 апреля любого следующего года оно зайдет почти точно в это же время. «Почти» объясняется несоизмеримостью продолжительности года и продолжительности суток, но ежегодные отклонения невелики, ими можно в первом приближении пренебречь
одним периодом, например, с 1 января по 31 декабря.
. Преимущества описываемой модели. График получен в результате рассмотрения «нематематической» модели, связанной с повседневной жизнью, путем составления таблицы значений времени захода Солнца. Этот график как бы рождается постепенно на глазах учащихся, а не задается в готовом виде.
В преподавании математики очень важна мотивационная сторона. Математическая задача воспринимается учащимися лучше, если она возникает как бы у них на глазах , фомулипуется после рассмотрения каких-то физических явлений или технических проблем.
Например,наблюдая за солнечным зайчиком, ребята замечают,что свет от одной точки до другой распространяется по прямой, выбирая кратчайший путь, равный длине отрезка между этими точками, Возникает вопрос: «По какому пути распространяется свет, если он идёт от одной точки к другой не прямо, а отражаясь от поставленного на его пути зеркала? Выбирает ли при этом свет наименьшее расстояние?»
Изучение распространения света прводит к сугубо геометрической задаче: «ТочкиА и В лежат в одной из полуплоскостей, образованных прямой l.На прямой l найти такую точку, чтобы сумма расстояний от неё до двух данных точек была наименьшей».
Решение. Построим точку А1, симметричную точке А относительно прямой l. Прямая А1В пересекает прямую l в точке X. Длина отрезка А1В есть кратчайшее расстояние между точками А1 и В. Но А1Х=АХ. Значит, ломаная АХВ наименьшая, удовлетворяющая условию задачи, а точка Х- искомая (рис 1)
Итак, физическая задача повлекла за собой задачу геометрическую, а от неё мы совершим кратчайший экскурс в историю. Природа ничего не делает напрасно Исходя из этого принципа, Герон Александрийский в начале нашего тысячелетия впервые высказал мысль о том, что свет распространяется кратчайшим путём, т. е. по прямой. Герон показал, что из всех ломаных линий АХВ, ведущих от предмета А к зеркалу Х и затем к глазу В , кратчайшей будет та, для которой выполняется: ∟АХХ2 =∟ВХХ1,
И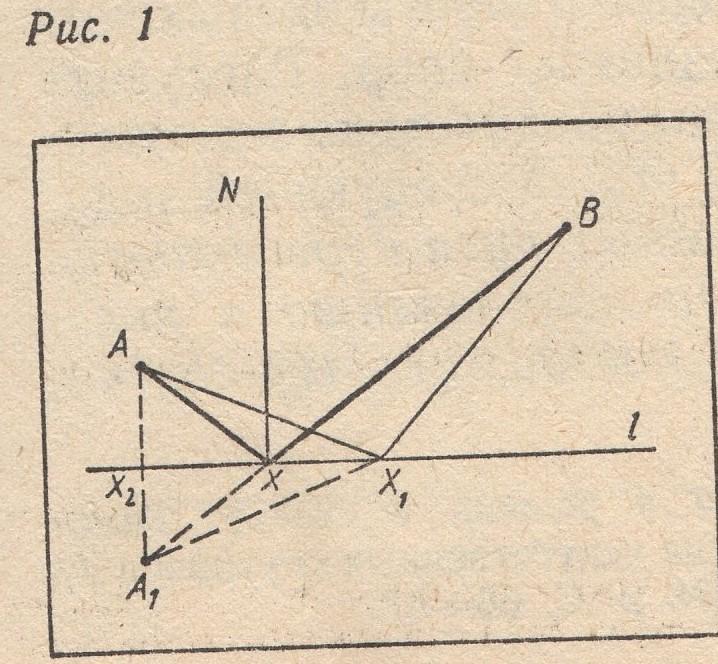
зучение распространения света прводит к сугубо геометрической задаче: «ТочкиА и В лежат в одной из полуплоскостей, образованных прямой l.На прямой l найти такую точку, чтобы сумма расстояний от неё до двух данных точек была наименьшей». Математические знания просто необходимы при изучении естественно-научных дисциплин, поэтому, прежде всего, необходимо чтобы материал изучался на уроках математики, а затем уже в других дисциплинах. Так, например, темы производная, векторы, логарифмы в курсе математики изучаются позже, чем по физике, поэтому происходит затруднения. Тема стандартный вид числа, которая в физике играет очень важную роль, на математике отводится всего лишь два часа, поэтому часто бывают проблемы при переводе единиц. При изучении геометрической прогрессии, при нахождении знаменателя встречаются задачи на извлечение корня более второй степени, хотя данная тема изучается лишь в 11 классе, и в 9 классе мы решаем методом подбора. Хотелось бы чтобы , вернули нам часы с 7 по 11 класс, для того чтобы хотя бы две четверти 11 класса мы не изучали новый материал , а систематизировали , обобщали , корректировали пробелы. Тем самым, готовились к экзаменам. Для преодоления этих трудностей необходимо пересмотреть некоторые разделы программ естественно-математического цикла.
Содержание понятия «грамотность» трансформируется исторически вместе с изменением требований общества. Изменение современной парадигмы образования под влиянием социальных факторов, тенденций развития общества определили необходимость рассмотрения вопроса формирования функциональной грамотности в сфере коммуникации как важное качество личности, определяющее успешность функционирования индивида в современном обществе.
Литература:
1. Министерство образования и науки Республики Казахстан Национальная академия образования им. И. Алтынсарина»Особенности формирования функциональной грамотности учащихся основной школы по предметам естественонаучного цикла» Астана 2014
2. Безрукова В.С. Основы духовной культуры (энциклопедический словарь педагога), 2000. - С.24-25.
3. Перминова Л.М. Минимальное поле функциональной грамотности (из опыта С.-Петербургской школы)/Педагогика. – 1999. - №2. - С. 26-29.
4. Мацкевич В.В., Крупник С.А. Всемирная энциклопедия: Философия. – Минск, 2001. – 687 c.
5. Максимова В.Н. Межпредметные связи в учебно-воспитательном процессе современной школы. - М.: Просвещение, 1986. – С. 25-31.
6. Файзулаева А. Из опыта трудового воспитания учащихся Математика в школе – 1983 №2 с 22
7. Колягин Ю. М., Пикан В.В. О прикладной и практической направленности обучения математики Математика в школе -1985 №6 с. 31
8.Рустюмова И.П., Рустюмова С.Т. Пособие для подготовки к единому национальному тестированию Алматы -2008
9.Шёнфельд Х. Что общего между заходом солнца и функцией синус? Математика в школе – 1993 №2 с75-76
10. Возняк Г.М. Прикладные задачи и мотивация обучения Математика в школе – 1990 №2 с.9
11 .Якунина М. С. Эстетическое воспитание на уроках математики Математика в школе -19832 №5 с.49
Қарақоға орта мектебі
Карагугинская средняя школа
Интеграция предметов естественнонаучного цикла в преподавании математики, как средство развития функциональной грамотности школьника.
Мұғалім: Кравченко Н.И.
Учитель: Кравченко Н.И.
2014- 2015 уч. год
