Домашняя работа
МОДЕЛИ МАССОВОГО ОБСЛУЖИВАНИЯ С ОЖИДАНИЕМ
1. Постановка задачи
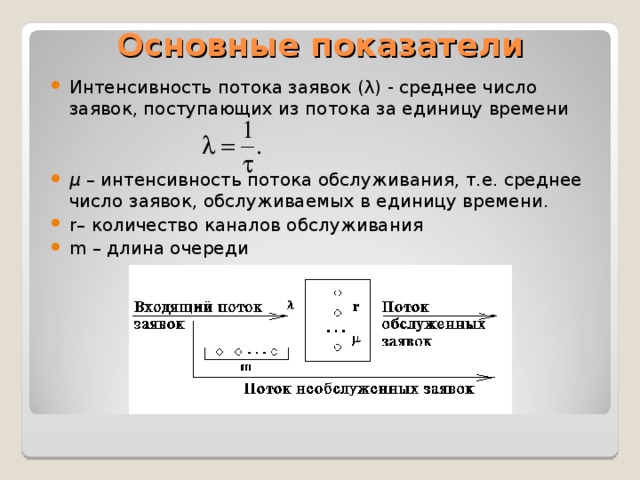
В систему, состоящую из  рубительных машин, поступает простейший поток бревен с интенсивностью
рубительных машин, поступает простейший поток бревен с интенсивностью  . Каждая машина имеет показательный закон рубки с интенсивностью
. Каждая машина имеет показательный закон рубки с интенсивностью  . Если количество бревен, поступивших в рубку, больше числа машин, то образуется очередь, длина которой ограничена и не может превосходить
. Если количество бревен, поступивших в рубку, больше числа машин, то образуется очередь, длина которой ограничена и не может превосходить 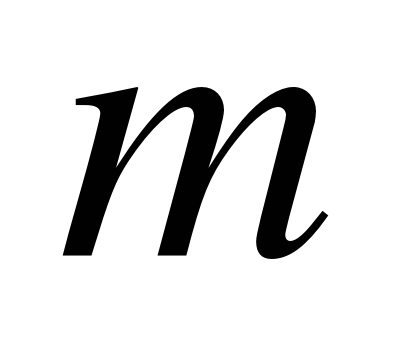 единиц. Требуется проанализировать работу цеха, как системы массового обслуживания с очередью конечной длины.
единиц. Требуется проанализировать работу цеха, как системы массового обслуживания с очередью конечной длины.
Для этого необходимо выполнить следующие пункты:
Указать возможные состояния системы и описать ее функционирование графом состояний. На графе показать интенсивности перехода из состояния в состояние.
Составить математическую модель функционирования системы для стационарного режима в виде системы линейных алгебраических уравнений. Найти решение системы.
Определить следующие стационарные характеристики эффективности системы:
а) вероятность, что 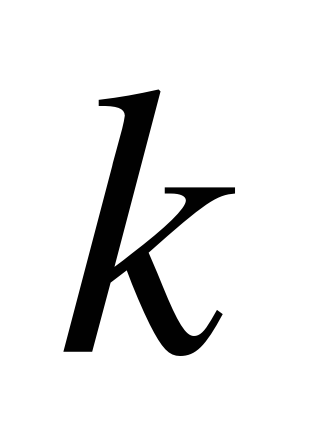 машин заняты рубкой (
машин заняты рубкой (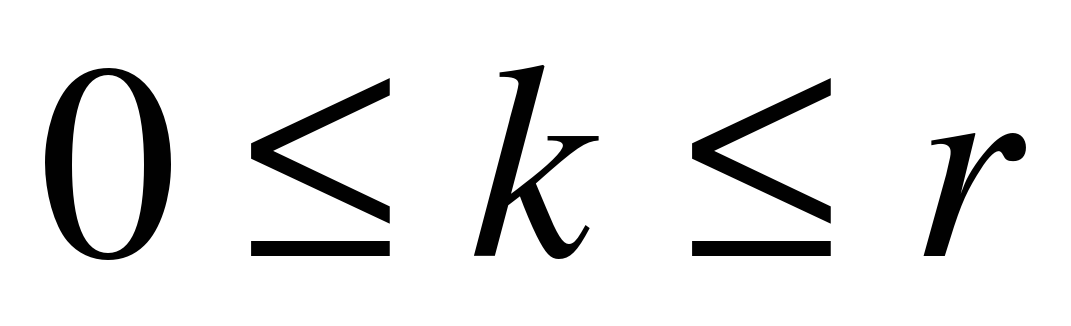 );
);
б) вероятность, что все машины заняты рубкой и 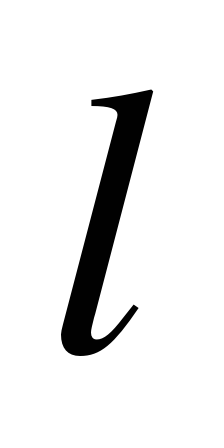 бревен находится в очереди (
бревен находится в очереди ( );
);
в) среднее число машин, занятых рубкой;
г) среднее число машин, свободных от рубки;
д) коэффициент загрузки машин;
е) коэффициент простоя машин;
ж) среднее число бревен в очереди.
2. Сведения из теории
2.1. Основные понятия
Системой массового обслуживания называется совокупность потока заявок (требований), поступающих в систему, и приборов (каналов), обслуживающих эти заявки. Поток заявок, как правило, носит случайный характер. Теория массового обслуживания занимается разработкой и анализом математических моделей, описывающих системы массового обслуживания.
Примерами систем массового обслуживания являются: автоматические телефонные станции и поступающие на них вызовы, магазины и покупатели, предприятия бытового обслуживания и клиенты, ремонтные мастерские и техника, требующая ремонта, ЭВМ и задачи, поступающие на решение, аэропорты и самолеты, требующие посадки, преподаватели и сдающие экзамены студенты, и т.д.
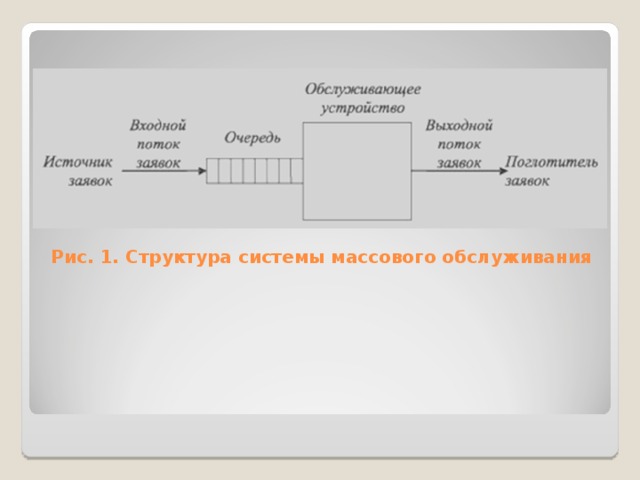
Неотъемлемой частью систем массового обслуживания является образование очереди на обслуживание, и поэтому теорию массового обслуживания принято называть также математической теорией очередей. Важно понимать, что в теории массового обслуживания речь идет о разработке математических моделей, обладающих достаточной степенью абстракции. Поэтому не важна природа обслуживаемых заявок и их физические свойства. Существенными являются лишь моменты появления этих заявок, так как от них зависит эволюция модели во времени. В абстрактной модели нет необходимости рассматривать физическую сторону процесса обслуживания. Обслужить заявку - это значит затратить на нее некоторое время в соответствии с принятой дисциплиной обслуживания. Всякая система массового обслуживания может быть изображена, как показано на рис.1.
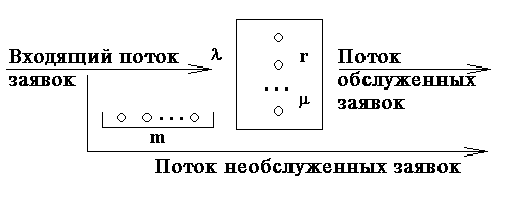
Рис.1. Схематическое изображение системы массового обслуживания
Опишем один из возможных вариантов функционирования системы. Предположим, что на обслуживание поступает поток заявок, который характеризуется параметром . В системе имеется  обслуживающих каналов (приборов). Если в системе есть свободные каналы, то вновь пришедшая заявка поступает на свободный канал и начинается ее обслуживание. Время обслуживания случайное и характеризуется параметром . По окончании обслуживания образуется поток обслуженных заявок. Если все каналы заняты обслуживанием, то вновь пришедшая заявка становится в очередь (поступает в бункер или накопитель) емкостью
обслуживающих каналов (приборов). Если в системе есть свободные каналы, то вновь пришедшая заявка поступает на свободный канал и начинается ее обслуживание. Время обслуживания случайное и характеризуется параметром . По окончании обслуживания образуется поток обслуженных заявок. Если все каналы заняты обслуживанием, то вновь пришедшая заявка становится в очередь (поступает в бункер или накопитель) емкостью 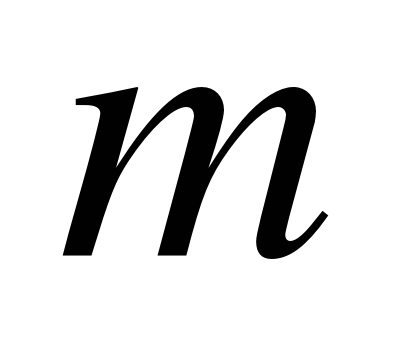 . Это значит, что в очереди может находиться не более, чем
. Это значит, что в очереди может находиться не более, чем 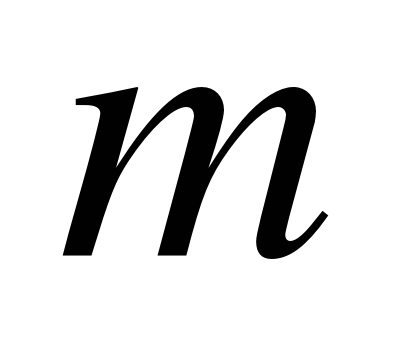 заявок. Если количество заявок в очереди превысит
заявок. Если количество заявок в очереди превысит 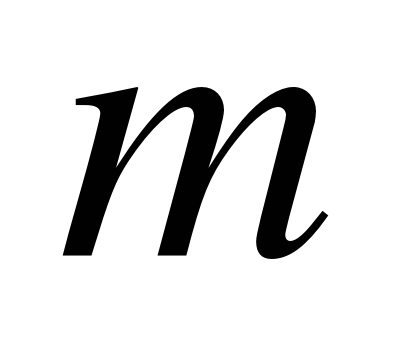 , то такие заявки покидают систему не обслуженными, образуя поток необслуженных заявок.
, то такие заявки покидают систему не обслуженными, образуя поток необслуженных заявок.
Работа системы массового обслуживания сопровождается рядом случайных факторов. Поток поступающих заявок представляет собой случайный процесс – число заявок является случайной функцией времени. Время, которое требуется для обслуживания одной заявки (время обслуживания) является случайной величиной.
Основными понятиями систем массового обслуживания являются следующие:
входящий поток заявок и его интенсивность,
очередь на обслуживание,
число обслуживающих каналов (приборов),
время обслуживания заявки,
дисциплина и приоритет обслуживания заявки (порядок выбора заявок из очереди),
потоки обслуженных и необслуженных заявок.
Системы массового обслуживания классифицируются в зависимости от вида потока заявок и характера их обслуживания. Различают системы с потерями (с отказами) и с очередью (с ожиданием). Если заявка поступает в систему с потерями в то время, когда все каналы заняты (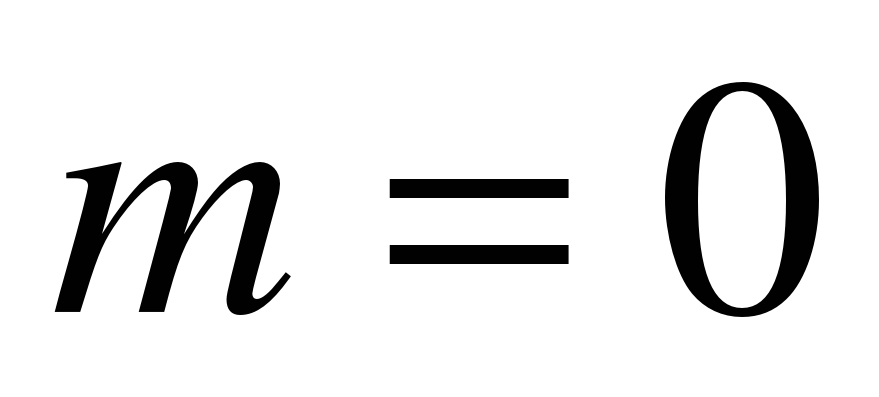 ), то она получает «отказ» и теряется. Примером такой системы может быть телефонная станция. В системах с очередью заявка, пришедшая в момент, когда каналы заняты, встает в очередь и ожидает, пока не освободится один из каналов. Существуют системы с неограниченной очередью, когда число мест в очереди не ограниченно (
), то она получает «отказ» и теряется. Примером такой системы может быть телефонная станция. В системах с очередью заявка, пришедшая в момент, когда каналы заняты, встает в очередь и ожидает, пока не освободится один из каналов. Существуют системы с неограниченной очередью, когда число мест в очереди не ограниченно (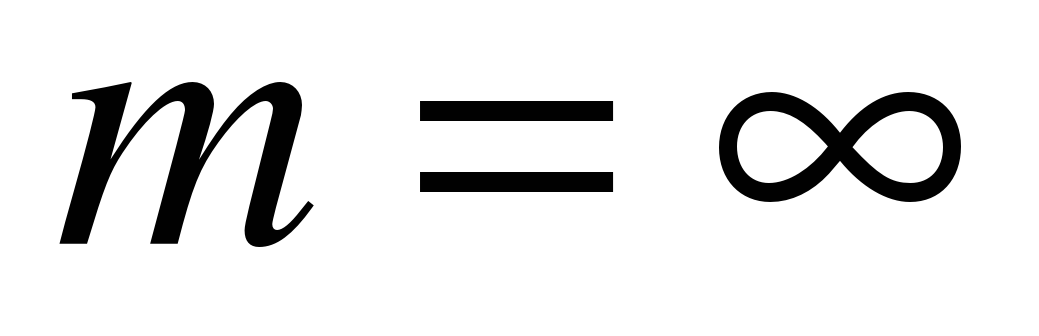 ) и системы с ограниченной очередью. Ограничения могут быть разными - по числу заявок, одновременно стоящих в очереди, по времени пребывания заявки в очереди, по времени работы системы и т.д.
) и системы с ограниченной очередью. Ограничения могут быть разными - по числу заявок, одновременно стоящих в очереди, по времени пребывания заявки в очереди, по времени работы системы и т.д.
По числу обслуживающих каналов различают одноканальные (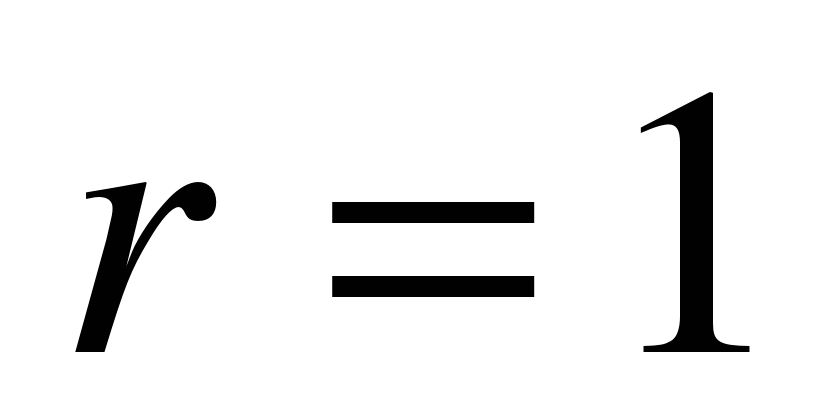 ) и многоканальные (
) и многоканальные (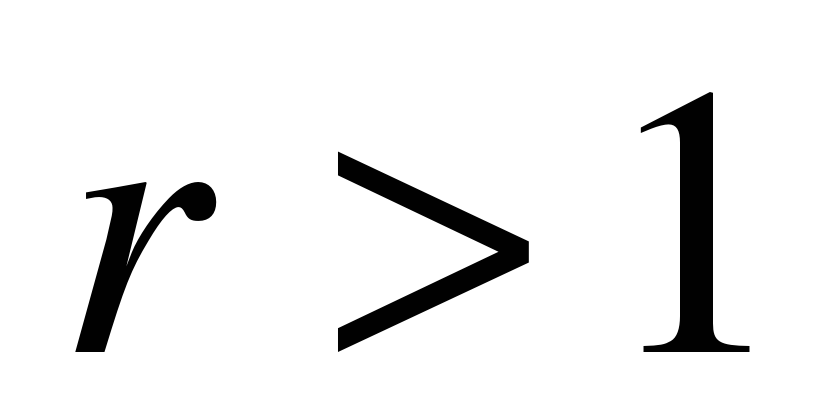 ) системы массового обслуживания. Для многоканальной системы будем предполагать, что каждая заявка может быть обслужена любым из каналов. Такая система каналов называется полнодоступным пучком.
) системы массового обслуживания. Для многоканальной системы будем предполагать, что каждая заявка может быть обслужена любым из каналов. Такая система каналов называется полнодоступным пучком.
В системах с очередью учитывается также дисциплина обслуживания. Обычно заявки обслуживаются в порядке их поступления в систему по принципу «первый пришел - первый обслужен» (прямой приоритет). Однако возможны и другие правила обслуживания заявок: «последний пришел - первый обслужен» (обратный приоритет), или «первой обслуживается заявка с заданным номером» (назначенный приоритет), или «первой обслуживается заявка со случайным номером» (случайный приоритет). Возможно также обслуживание заявки вне очереди. При этом заявка с более высоким приоритетом, поступив в систему, может оборвать уже начавшееся обслуживание заявки с меньшим приоритетом, а может дождаться окончания ее обслуживания. В первом случае говорят об абсолютном, а во втором - об относительном приоритете.
Основоположником теории массового обслуживания принято считать датского математика А.К.Эрланга, который в 1909 г. опубликовал важные результаты, полученные им при изучении математических моделей телефонных систем. В настоящее время модели и методы массового обслуживания находят приложения во многих областях науки и техники, начиная с контроля над приземлением самолетов и кончая теорией управления запасами, от исследований, связанных с ростом бактерий, – до составления больничных графиков.
3. Задача: Исходные данные для анализа системы массового обслуживания содержатся в табл.1.
Таблица 1
3.1. Граф состояний
Перечислим возможные состояния системы:
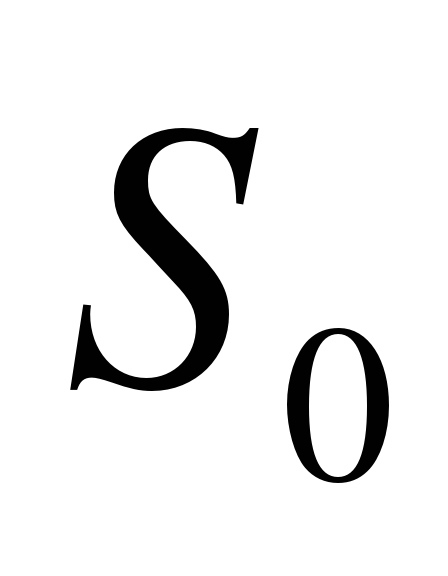 – в системе бревен нет, машины свободны от рубки;
– в системе бревен нет, машины свободны от рубки;
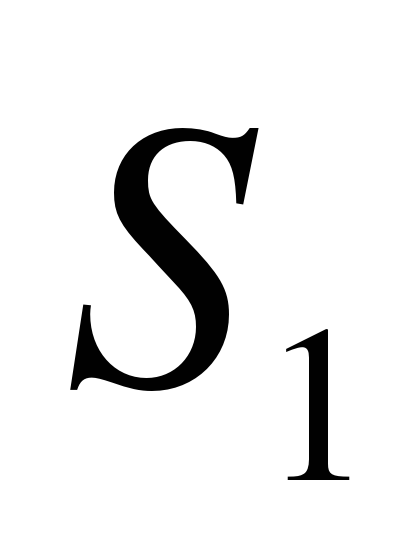 – в системе 1 бревно, одна машина занята рубкой;
– в системе 1 бревно, одна машина занята рубкой;
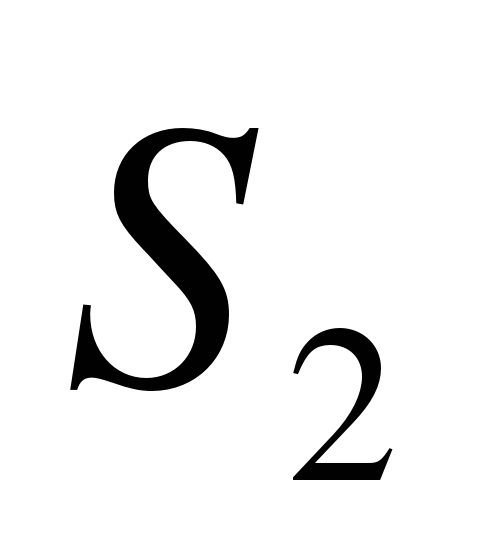 – в системе 2 бревна, две машины заняты рубкой;
– в системе 2 бревна, две машины заняты рубкой;
 – в системе 3 бревна, две машины заняты рубкой, одно бревно находится в очереди;
– в системе 3 бревна, две машины заняты рубкой, одно бревно находится в очереди;
 – в системе 4 бревна, две машины заняты рубкой, два бревна находятся в очереди.
– в системе 4 бревна, две машины заняты рубкой, два бревна находятся в очереди.
Граф состояний приведен на рис.4. Переходы слева направо связаны с поступлением в систему очередного бревна, поэтому все интенсивности переходов одинаковы и равны 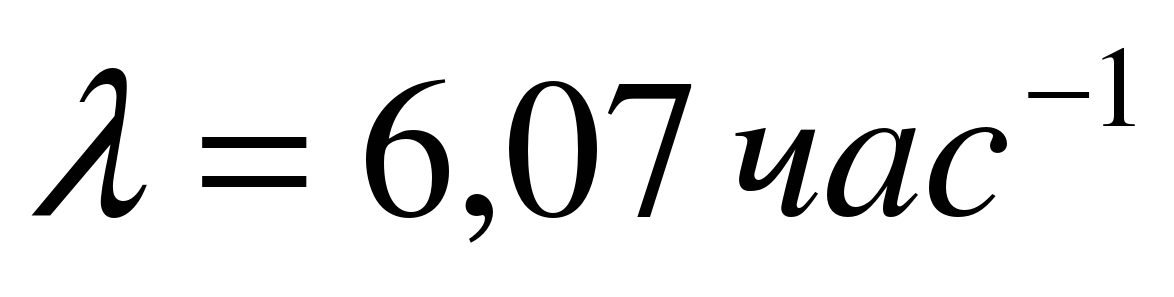 . Переходы справа налево обусловлены окончанием рубки бревна. В состоянии
. Переходы справа налево обусловлены окончанием рубки бревна. В состоянии 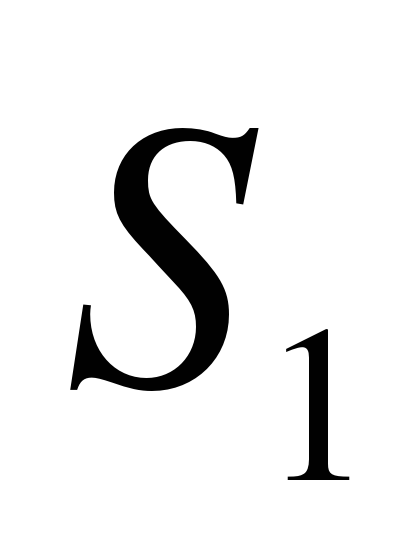 работает одна машина, поэтому интенсивность перехода из состояния
работает одна машина, поэтому интенсивность перехода из состояния 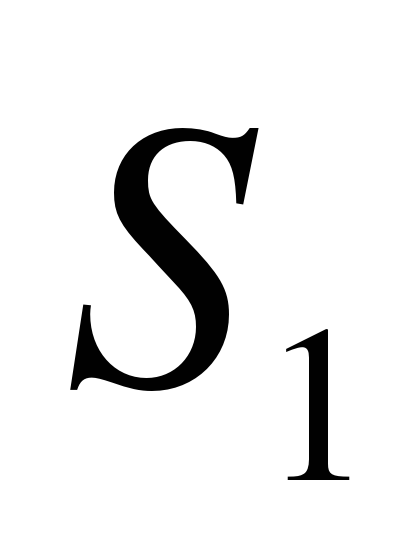 в состояние
в состояние 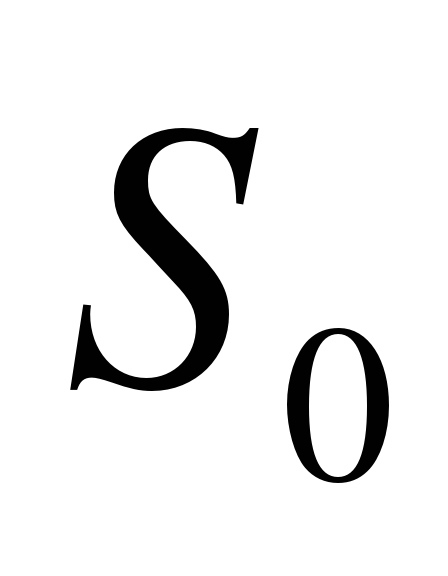 равна
равна 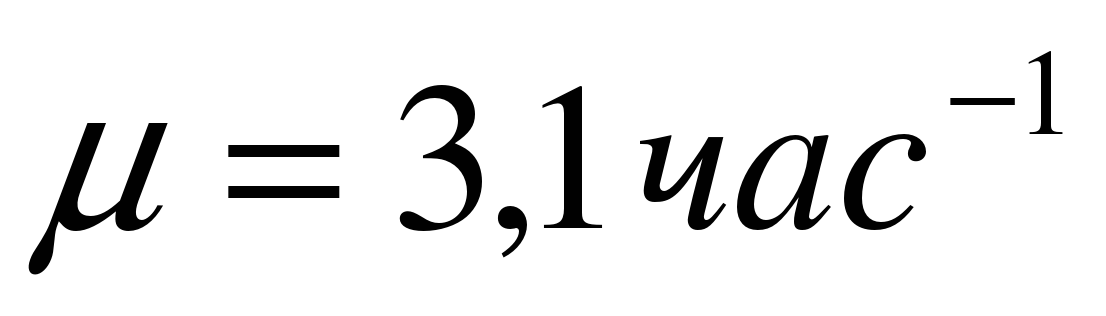 . В состояниях
. В состояниях 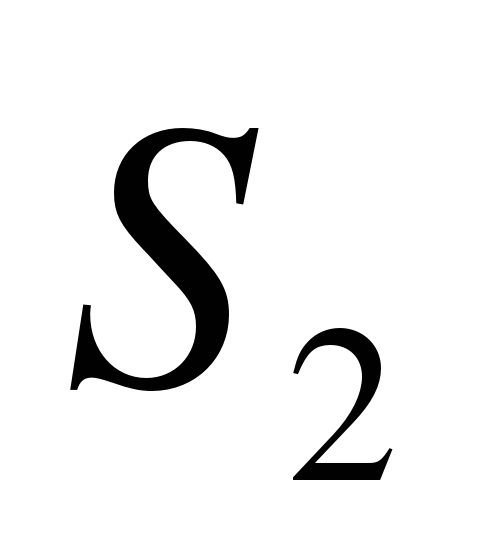 ,
,  и
и  работает две машины, поэтому соответствующие интенсивности переходов равны
работает две машины, поэтому соответствующие интенсивности переходов равны 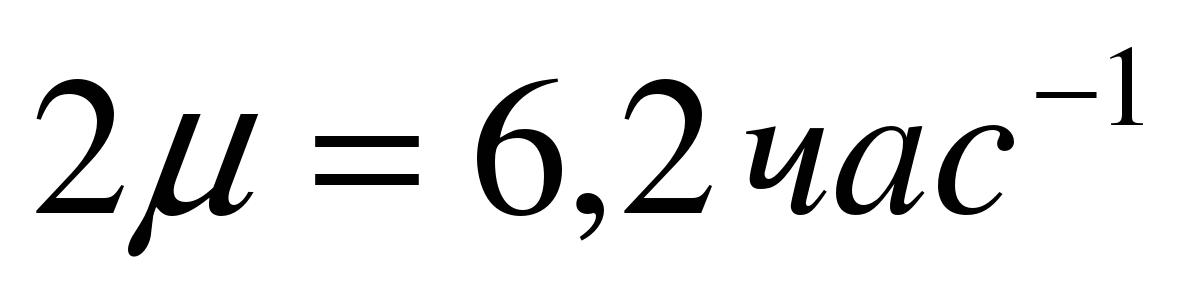 .
.
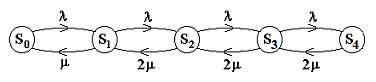
Рис.4. Граф состояний системы 
3.2. Математическая модель стационарного режима
Пусть 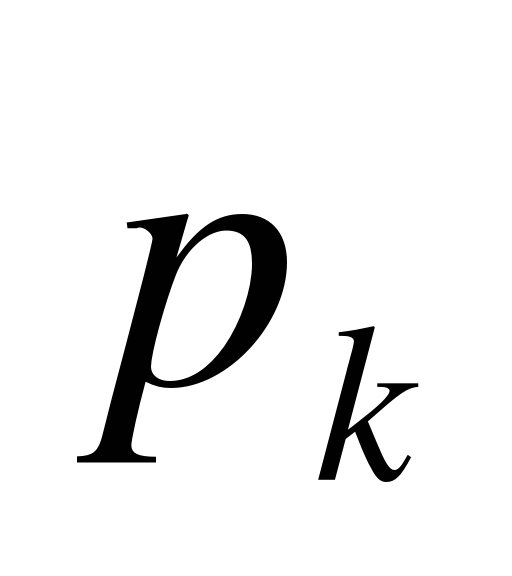 – стационарная вероятность пребывания системы в состоянии
– стационарная вероятность пребывания системы в состоянии 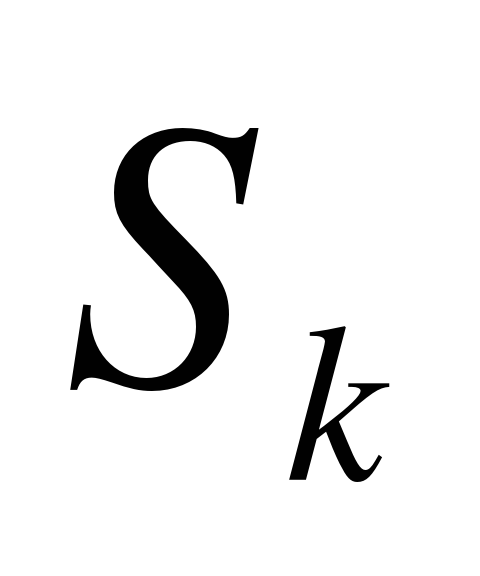 ,
, 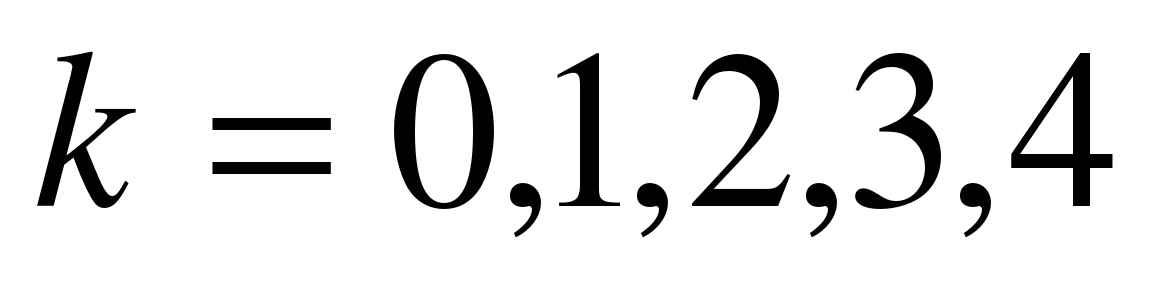 . Тогда имеет место следующая система алгебраических уравнений, описывающая стационарный режим:
. Тогда имеет место следующая система алгебраических уравнений, описывающая стационарный режим:
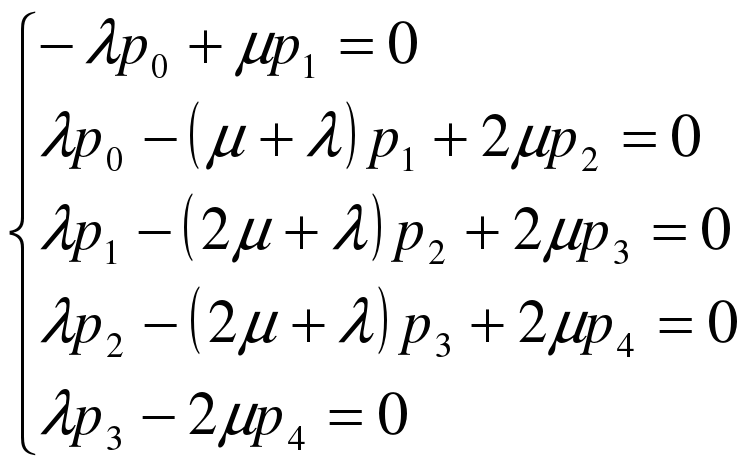 (12)
(12)
Эту систему следует решать вместе с условием нормировки
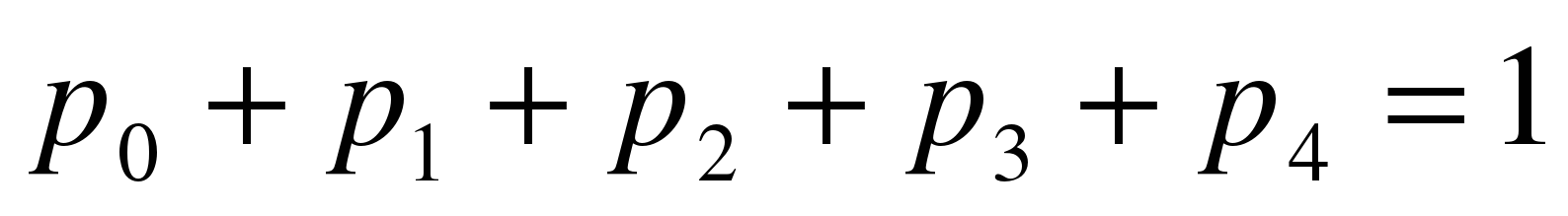 . (13)
. (13)
Воспользуемся для этой цели электронной таблицей Excel. На Листе 1, как показано в табл.5, в ячейки B1 и B2 поместим значения интенсивностей  и
и  . Блок ячеек D3 : H3 зарезервируем для записи значений искомых вероятностей
. Блок ячеек D3 : H3 зарезервируем для записи значений искомых вероятностей 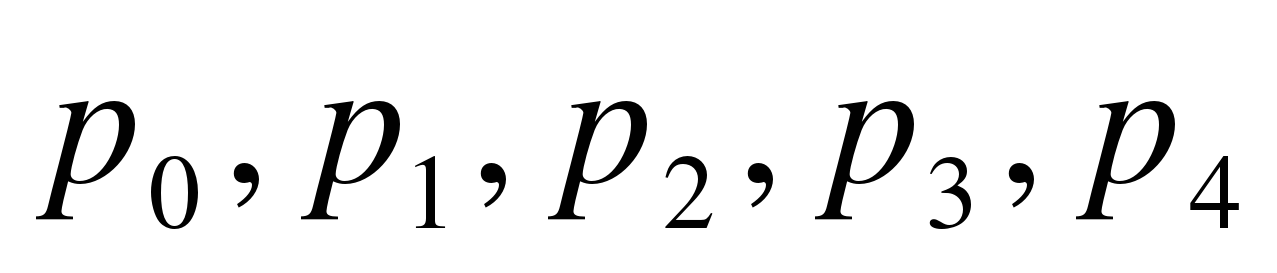 (отмечены желтым цветом). Эти ячейки сначала пустые. В блоке ячеек D4 : H7 поместим коэффициенты при неизвестных системы (12), за исключением последнего уравнения. Последнее уравнение системы (12) заменим условием нормировки (13), тогда в блоке ячеек D8 : H8 будут располагаться «единицы».
(отмечены желтым цветом). Эти ячейки сначала пустые. В блоке ячеек D4 : H7 поместим коэффициенты при неизвестных системы (12), за исключением последнего уравнения. Последнее уравнение системы (12) заменим условием нормировки (13), тогда в блоке ячеек D8 : H8 будут располагаться «единицы».
Таблица 5
|
| A | B | C | D | E | F | G | H | I | J |
| 1 | | 6,07 |
| Решение системы алгебраических уравнений |
| 2 | | 3,1 |
| 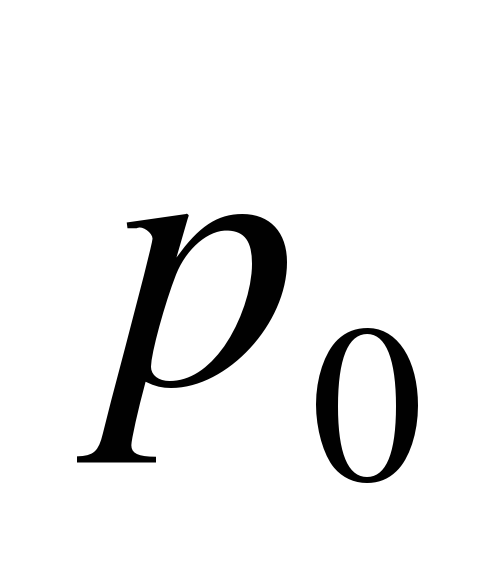
| 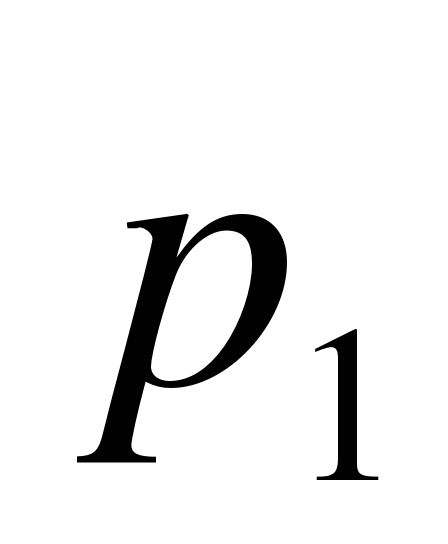
| 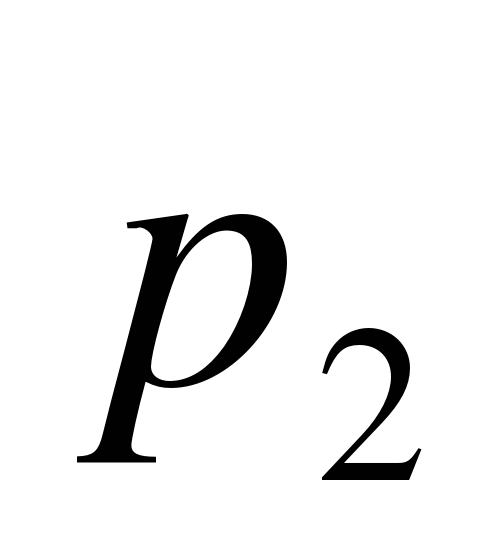
| 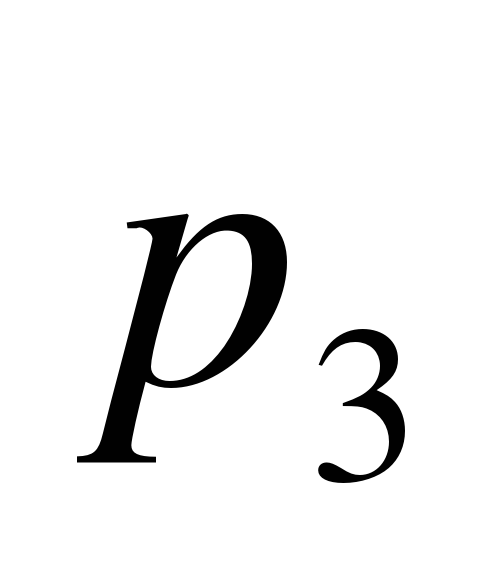
| 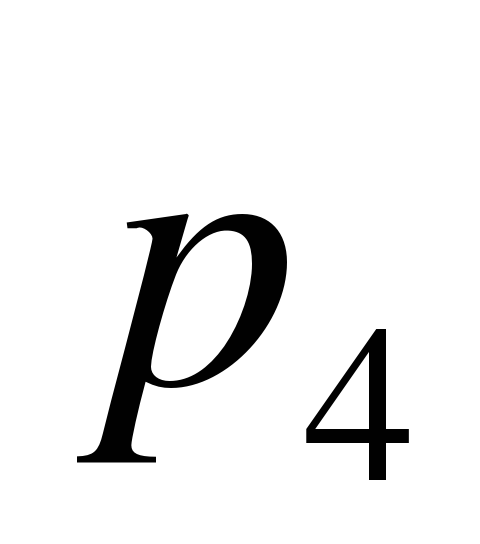
|
|
|
| 3 |
|
|
| 0,116423 | 0,227965 | 0,223185 | 0,218505 | 0,213923 |
|
|
| 4 |
|
|
| -6,07 | 3,1 | 0 | 0 | 0 | 4,17E-08 | 0 |
| 5 |
|
|
| 6,07 | -9,17 | 6,2 | 0 | 0 | 4E-08 | 0 |
| 6 |
|
|
| 0 | 6,07 | -12,27 | 6,2 | 0 | 1,05E-07 | 0 |
| 7 |
|
|
| 0 | 0 | 6,07 | -12,27 | 6,2 | 1,03E-07 | 0 |
| 8 |
|
|
| 1 | 1 | 1 | 1 | 1 | 1,000001 |
|
Блок ячеек I4 : I8 содержит формулы для записи левых частей системы уравнений (10) и (11), а именно, в клетку I4 поместим формулу
= СУММПРОИЗВ( $D$3 : $H$3 ; D4 : H4 ),
которую протянем на блок ячеек I5 : I8. В блоке ячеек J4 : J7 содержатся правые части системы (12), равные «нулям».
Обращение к процедуре «Поиск решения» позволит найти решение системы уравнений (12). Для этого следует в появившемся окне указать:
целевую ячейку, в данном случае I8, равную значению 1 (условие нормировки);
изменяемые ячейки, в данном случае блок D3 : H3;
ограничение, в данном случае I4 : I7 = J4 : J7.
После нажатия клавиши «Выполнить» в блоке D3 : H3 получим решение системы уравнений.
3.3. Стационарные характеристики СМО
На основе полученных значений вероятностей пребывания системы в состояниях определяются требуемые показатели эффективности стационарного режима.
Пусть – число машин, занятых рубкой. Это есть случайная величина с возможными значениями: 0, 1, 2. Вероятности этих значений соответственно равны
,
,
.
Тогда среднее число машин, занятых рубкой, есть математическое ожидание случайной величины , которое равно
.
Следовательно, среднее число работающих машин равно ___
Пусть – число машин, свободных от рубки. Это есть случайная величина с возможными значениями: 0, 1, 2. Вероятности этих значений соответственно равны
,
,
.
Тогда среднее число машин, свободных от рубки, есть математическое ожидание случайной величины , которое равно
.
Следовательно, среднее число простаивающих машин равно ____. Общее число занятых и свободных от рубки машин равно
.
Коэффициент загрузки машин равен отношению среднего числа загруженных машин к общему числу машин в цехе, т.е.
.
Коэффициент простоя машин равен отношению среднего числа машин, свободных от рубки, к общему числу машин в цехе, т.е.
.
Пусть – число бревен в очереди. Это есть случайная величина с возможными значениями: 0, 1, 2. Вероятности этих значений соответственно равны
,
,
.
Тогда среднее бревен в очереди есть математическое ожидание случайной величины , которое равно
.
Таким образом, среднее число бревен, находящихся в очереди на рубку, равно ____
Выводы:
5


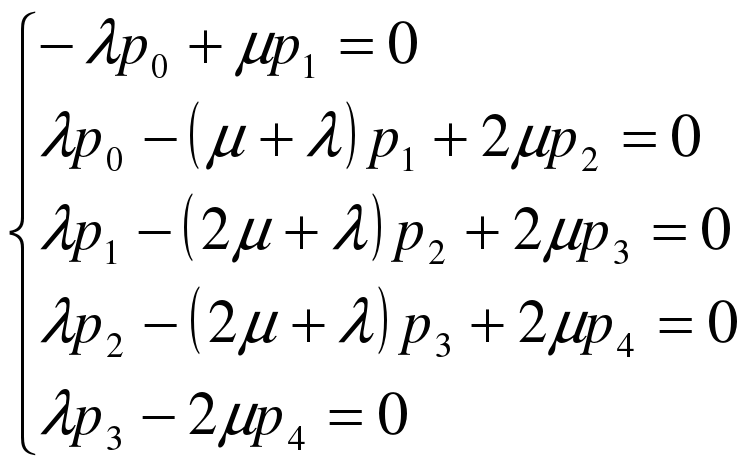 (12)
(12)