| Этап урока | Деятельность учителя | Деятельность обучающихся |
| Мотивация к учебной деятельности | Приветствие обучающихся
|
|
| Слайд 1 Я очень хочу, чтобы урок получился интересным, познавательным, чтобы мы вместе повторили и закрепили то, что знаем и постарались открыть новые секреты в нашей удивительной стране «Геометрия». Для этого мы настроимся на урок, так как задания, которые я предложу, требуют внимания, дисциплины, знания формул, свойств и быстрых вычислительных навыков.
|
|
| Слайд 2 «Знания усваиваются только в ходе собственной работы обучаемого с этими знаниями» Л.С. Выготский Эпиграф урока, как понимаете эти слова? | Объясняют смысл эпиграфа |
| Проверка домашней работы | 1.Радиус основания конуса 3 м, высота 4 м. Найдите образующую.
|
Ответ: 5 м
|
| 2.Образующая конуса L наклонена к плоскости основания под углом в 300. Найдите высоту.
| Ответ:1/2 L |
| 3.В прямоугольном треугольнике АВС, (рисунок), 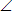 В = 600, ВС = 1. Найдите длину катета АС, используя теорему Пифагора. В = 600, ВС = 1. Найдите длину катета АС, используя теорему Пифагора. 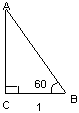
| Ответ: 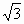 |
| 4. MNK прямоугольный (рисунок), MNK прямоугольный (рисунок), 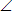 К = 450, катет KN = 8. Найдите длину катета MN. К = 450, катет KN = 8. Найдите длину катета MN. 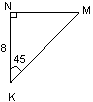
| Ответ: 8 |
| 5.Высота конуса равна 6, радиус основания равен 8. Найдите боковую поверхность.
| Ответ: 80П |
| Актуализация знаний. Устная работа | Слайд 3 Задания на повторение из егэ |
|
Площадь боковой поверхности цилиндра 15П, а высота - 3. Найти диаметр основания. | Ответ: 5 |
Основанием прямой треугольной призмы служит прямоугольник с катетами 6 и 8. Площадь её поверхности равна 288. Найти высоту призмы. | Ответ: 12 |
| На доске фигуры (треугольник, параллелограмм, квадрат, трапеция, прямоугольник, ромб) из бумаги и карточки с формулами для вычисления площадей этих фигур. |
|
| Назовите фигуры. | Треугольник, параллелограмм, квадрат, трапеция, прямоугольник, ромб. |
| Как их можно назвать одним словом? | Многоугольники. |
| Соотнесите фигуры и формулы площадей. | 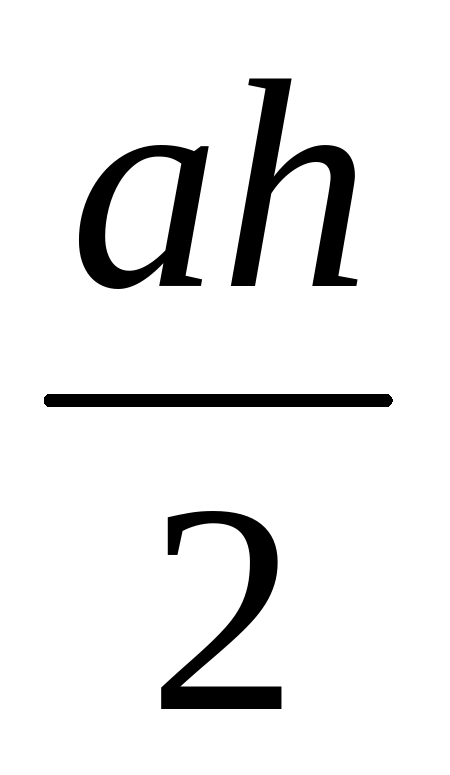 ; ; 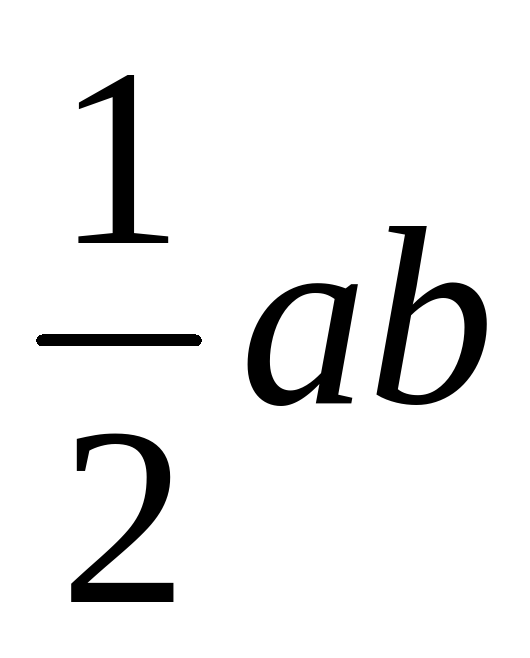 ; ; 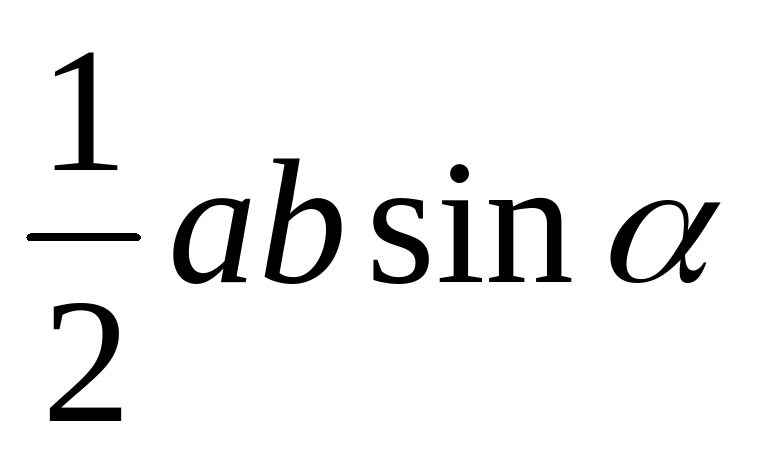 ; ; 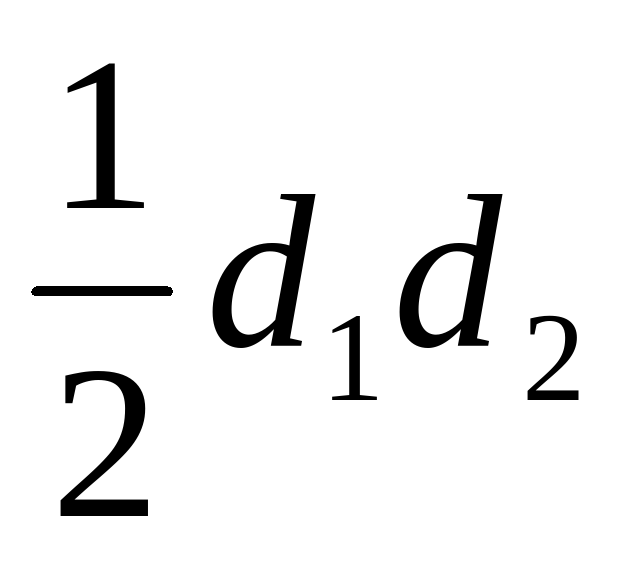 ; ; 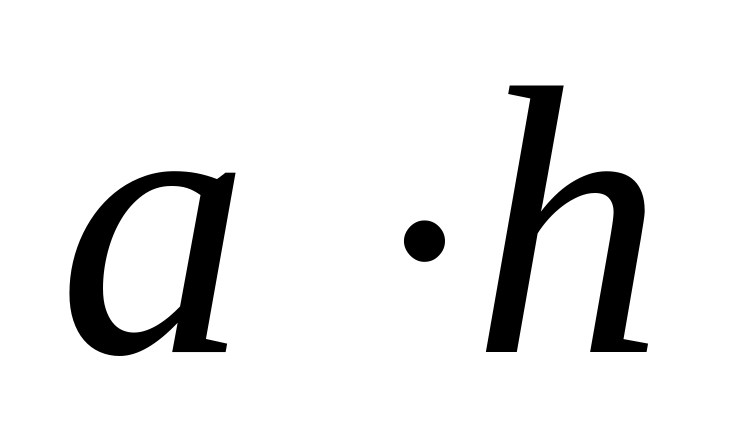 ; ; 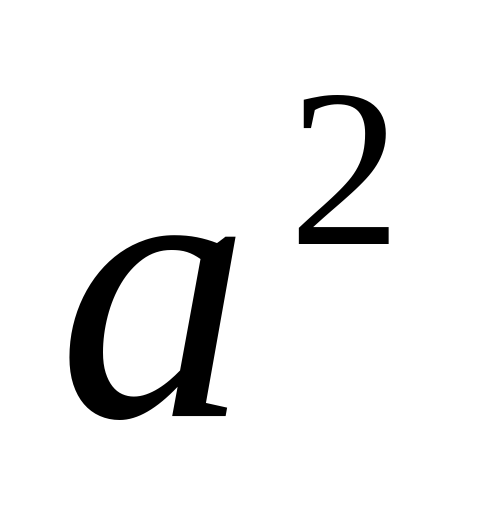 ; ; 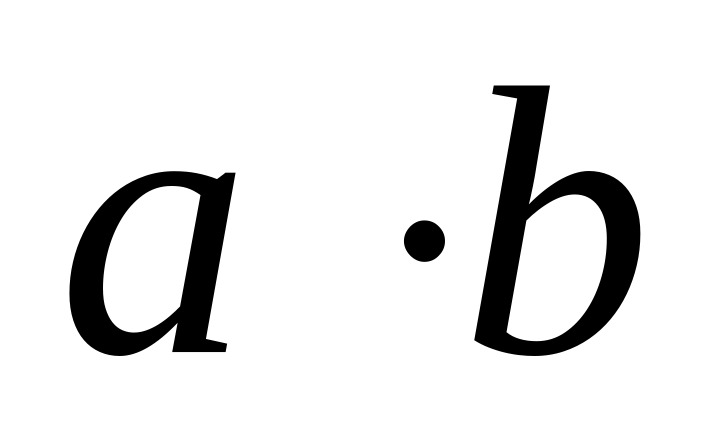 ; ; 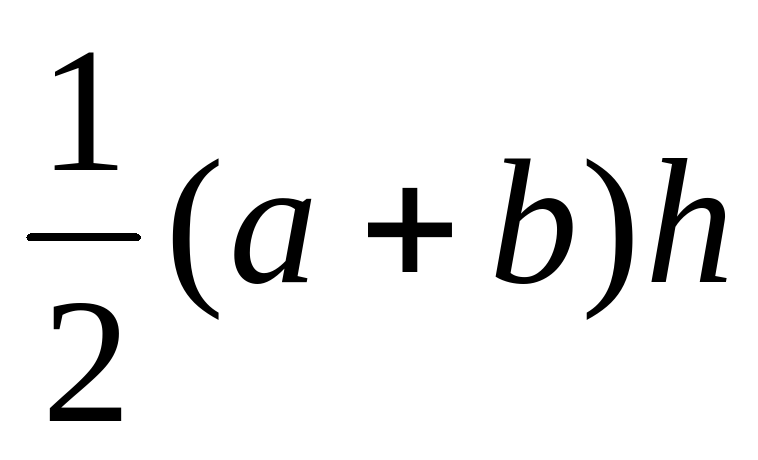
|
| Какая из формул подходит для вычисления площади пола комнаты? | 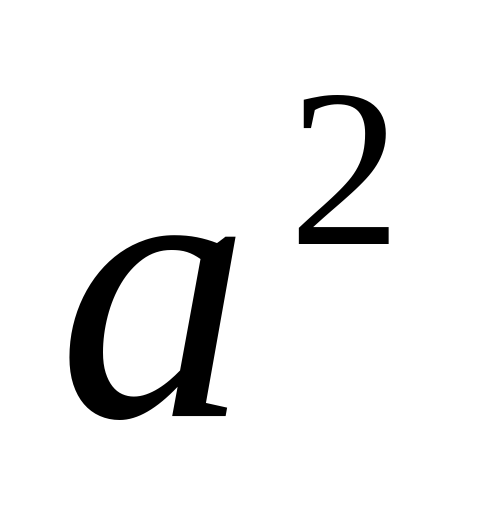 ; ; 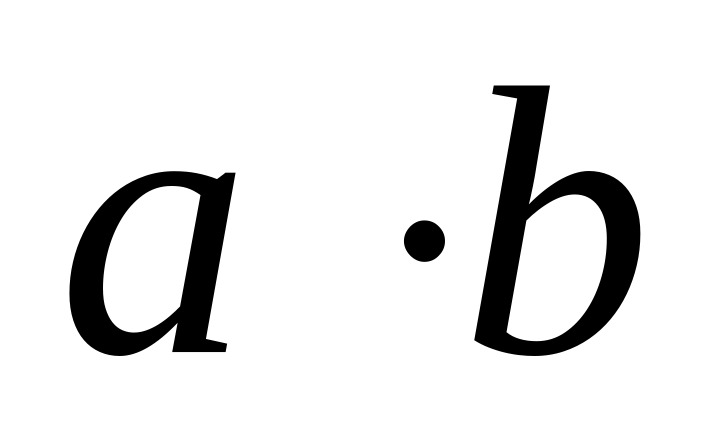 |
| Слайд 4 Н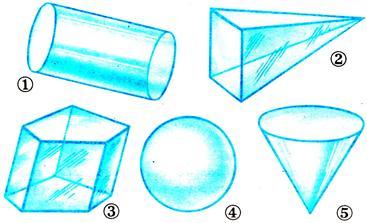 а рисунке изображены различные геометрические тела. Какие из них являются многогранниками? а рисунке изображены различные геометрические тела. Какие из них являются многогранниками?
| Ответ: 2 – пирамида, 3 - 5-тиугольная призма. |
|
| Слайд 5 Повторим формулы площади поверхностей геометрических тел. Карточки - таблички с формулами | 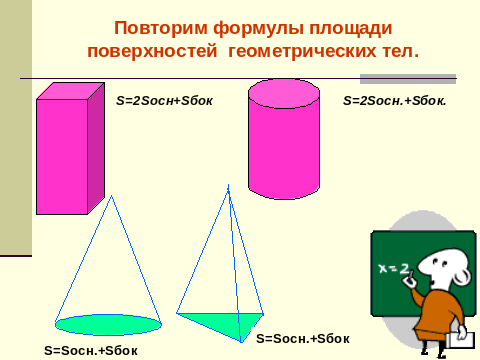 |
| Целеполагание и построение проекта | Слайд 6 Ребусы  | Три + зима = призма
Кубок = куб
Пирог + рама + еда = пирамида |
| О чем же пойдет речь на нашем уроке? | О многогранниках. |
| Какие многогранники знаете? | Пирамида, параллелепипед, куб, призма, тетраэдр, икосаэдр, октаэдр, додекаэдр. |
| Фронтальный опрос: Как называется фигура, состоящая из двух равных многоугольников, лежащих в параллельных плоскостях, и n - параллелограммов?
|
Призма |
| Как называются стороны граней многогранника?
| Ребра |
| Как называется отрезок, соединяющий две вершины, не принадлежащие одной грани?
| Диагональ многогранника |
| У какой призмы боковые ребра перпендикулярны к основаниям?
| Прямая призма |
| Как называется высота боковой грани правильной пирамиды?
| Апофема |
| Какой многоугольник лежит в основании правильной призмы? | Правильный многоугольник |
| Какая фигура является боковой гранью призмы?
| Параллелограмм |
| Приведите примеры предметов из окружающего мира, которые имеют вид призм. | Коробка, ящик, шкаф…. |
| Слайд 7 Какие еще объемные тела мы изучали на уроках геометрии? 


|
Шар
Конус
Цилиндр
|
| Чем отличаются многоугольники от многогранников? | Объемом. |
| Как вы думаете, какова тема нашего урока? | Объемы тел. |
| Слайд 8 Какую цель поставим перед собой? |  |
| А для чего вам, как будущим учителям начальных классов, уметь находить объём данных геометрических тел? | Пригодится в повседневной жизни, например, при выполнении ремонта, посмотреть учебники из начальной школы на данную тему |
| Что называется площадью многоугольника? | Площадь многоугольника – это положительная величина той части плоскости, которую занимает многоугольник. |
| Что такое объём тела? |
|
| Понятие объема тела вводится по аналогии с понятием площади плоской фигуры. Из курса планиметрии известно, что каждый многоугольник имеет площадь, которая измеряется с помощью выбранной единицы измерения площадей. В качестве единицы измерения площадей обычно берут квадрат, сторона которого равна единице измерения отрезков. Слайд 9 Аналогично будем считать, что каждое из рассматриваемых нами тел имеет объем, который можно измерять с помощью выбранной единицы измерения объемов. | Объем тела – это положительная величина той части пространства, которую занимает геометрическое тело.
|
| В чем измеряется площадь плоских фигур? | За единицу измерения площадей берут квадрат, сторона которого равна единице измерения отрезков. |
| Какие единицы измерения площадей вы уже знаете? | 1 км2, 1 м2, 1 дм2, 1 см2, 1 мм2 , 1 а, 1 га и т.д.
|
| Что примем за единицу измерения объемов? | За единицу измерения объемов примем куб, ребро которого равно единице измерения отрезков. Куб с ребром 1 см называют кубическим сантиметром и обозначают см3. |
| Какие единицы измерения объёма вы уже знаете? | 1 м3, 1 дм3, 1 см3 , 1 мм3 и т.д.
|
| Слайд 10 Процедура измерения объемов тел аналогична процедуре измерения площадей. При выбранной единице измерения объем каждого тела выражается положительным числом, которое показывает, сколько единиц измерения объемов и частей единицы содержится в данном теле. |
|
| Слайд 11 Мы с вами уже знакомы из курса планиметрии со свойствами площадей. Давайте вспомним первое свойство: (ученики используют подсказку на слайде). | Свойство 1: - Равные многоугольники имеют равные площади.
|
| Мы с вами можем сформулировать первое свойство объема тел, используя в качестве подсказки рисунок слайда. | Равные тела имеют равные объемы. |
| Равенство двух фигур, в частности двух тел, в стереометрии определяется так же, как и в планиметрии: два тела называются равными, если их можно совместить наложением. |
|
| Слайд 12 Рассмотрим еще одно свойство объемов. Для этого мы вспомним второе свойство из курса планиметрии: (ученики используют подсказку на слайде).
| Свойство 2: – Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников. SF = SF1+ SF2+ SF3 + SF4
|
| Итак, давайте выведем второе свойство объема. | Если тело составлено из нескольких тел, то его объем равен сумме объемов этих тел. VF = VF1 + VF2 |
| Слайд 13 Мы с вами вспомнили некоторые свойства из курса планиметрии и рассмотрели 2 свойства объемов. Сформулируйте – какие фигуры называются равновеликими? |
Равновеликими называются геометрические фигуры, имеющие равные площади SF = SF1 . |
| Сформулируйте – какие тела называются равновеликими? | Равновеликими называются тела, объемы которых равны VF= VF1 |
| Освоение новых знаний | Слайд 14 Каждое тело занимает часть пространства: кирпич – больше, чем карандаш. Чтобы можно было сравнивать такие части пространства, вводят понятие объема. В повседневной жизни нам часто приходится определять объемы различных тел. Например, коробки, банки. В житейской практике единицами объема служили меры емкости, используемые для хранения сыпучих и жидких тел. Среди них английские меры: Бушель – 36,4 дм3 Галлон – 4,5 дм3 Баррель (сухой) – 115,628 дм3 Баррель (нефтяной) – 158,988 дм3 Английский баррель для сыпучих веществ - 163,65 дм3. Меры когда-то, применявшиеся в России: Ведро – 12 дм3 Бочка – 490 дм3 Поиск формул, позволяющих вычислять объемы различных тел, был долог. В древнеегипетских папирусах, в вавилонских клинописных табличках встречаются правила для нахождения объема усеченной пирамиды, но не сообщаются правила для вычисления объема полной пирамиды. Определять объемы призмы, пирамиды, цилиндра и конуса умели древние греки еще задолго до Архимеда. Но только он имел общий метод, позволяющий определить любую площадь или объем. Идеи Архимеда легли в основу интегрального исчисления. Сам ученый определил с помощью своего метода площади и объемы почти всех тел, которые рассматривались в античной математике. На могильной плите Архимеда, как завещал ученый, был изображен цилиндр с вписанным шаром, а эпитафия говорила о величайшем открытии Архимеда – о том, что объемы этих тел относятся как 3 : 2. А о достоверности этой задачи чуть позже, когда рассмотрим тему объема шара.
|
| Слайд 15 В курсе математики 5-го класса мы с вами уже познакомились с прямоугольным параллелепипедом. Давайте воспользуемся чертежом и вспомним основные элементы прямоугольного параллелепипеда и формулы уже известные нам. Следствие 1: Объем прямоугольного параллелепипеда равен произведению площади основания на высоту. | Измерения – а – длина; b – ширина; с – высота. Известные формулы: V = a.b.c
Sосн = a.b
V = Sосн.H 
|
|
| Слайд 16 А как называется прямоугольный параллелепипед у которого все измерения равны? Длина куба а = а; ширина в = а; высота с = а. Подставим имеющиеся данные в формулу V=a.b.c в результате чего мы получаем: | К уб уб
V = a.а.а = а3 V = а3
|
| Слайд 17 А сейчас мы рассмотрим прямую призму, основанием которой является прямоугольный треугольник. | 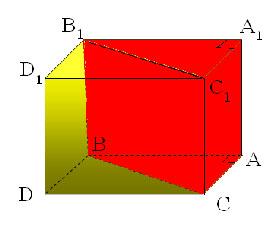 По модели треугольной призмы вывести формулу для вычисления объёма данной призмы. По модели треугольной призмы вывести формулу для вычисления объёма данной призмы.
|
|
| Какое свойство вам известно о прямой призме, основанием которой является прямоугольный треугольник? | Прямая призма, основанием которой является прямоугольный треугольник, образуется путем разрезания прямоугольного параллелепипеда на две равные части. |
| Самостоятельно определить формулу для нахождения объема прямой призмы Следствие 2 – Объем прямой призмы, основанием которой является прямоугольный треугольник, равен произведению основания на высоту.
| Достроим данную треугольную призму до параллелепипеда Vпр= 1/2Vпар = 1/2Sосн • H=1/2•2SпрH = SпрH или 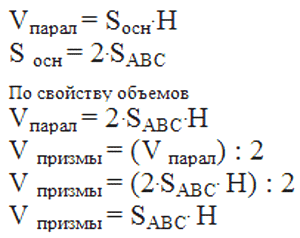
|
|
| Слайд 18 Задача. Диагональ правильной четырёхугольной призмы равна 3,5 см, а диагональ боковой грани 2,5 см. Найдите объём призмы. 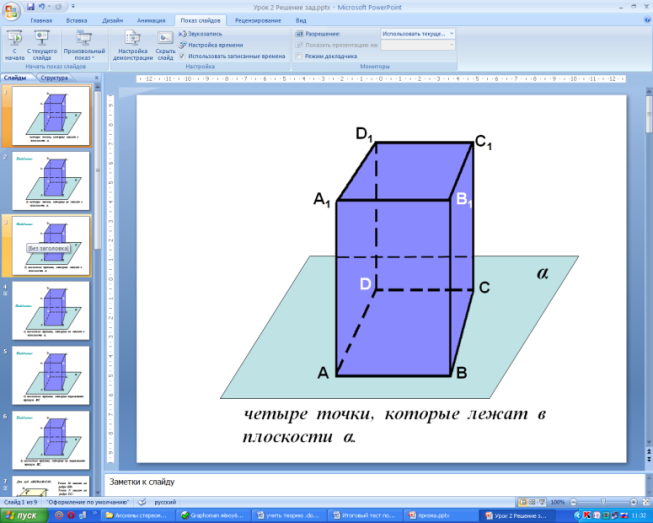
| Дано: ABCDA1B1C1D1 – прав. призма, AC1 = 3,5 см, BC1 = 2,5 см. Найти V. Решение. Так как ABCDA1B1C1D1 – прав. призма, то ABCD – квадрат, т. е. угол ABC – прямой. По теореме о трёх перпендикулярах BC1 ┴ AB. Из треугольника ABC1 Найдём сторону основания 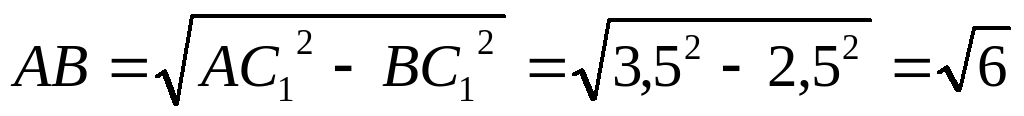 см. Площадь основания равна 6 см2. см. Площадь основания равна 6 см2. Из треугольника BCC1 найдём высоту CC1. 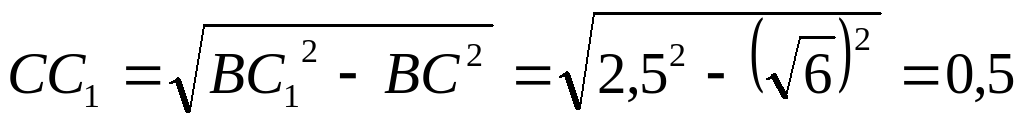 см. см. Итого V = SH = 6▪0,5 = 3 см3. Ответ: 3 см3.
|
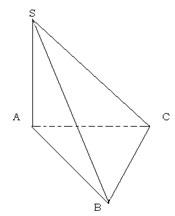
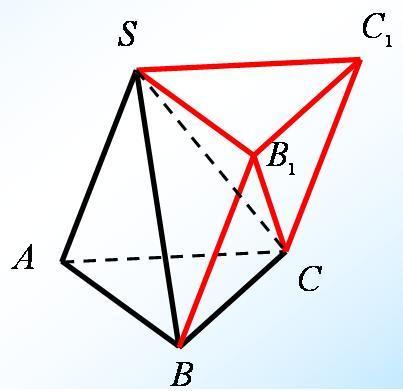
| Опыт 1 Демонстрируются 2 сосуда: один имеющий форму призмы, другой форму – пирамиды. Следствие 3: Объем любой пирамиды равен одной трети произведения площади основания на высоту. Или Слайд 19 Опыт 2 А сейчас мы с вами найдем объем пирамиды. Достроим пирамиду ABCS до призмы. 1. Пусть SABC – треугольная пирамида с вершиной S и основанием АВС. 2. Дополним эту пирамиду до треугольной призмы с тем же основанием и высотой. 3. Эта призма составлена из трех пирамид: 1) данной пирамиды SABC. 2) пирамиды SCC1B1. 3) и пирамиды SCBB1. 4. У второй и третьей пирамид равные основания 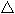 СС1В1 и СС1В1 и 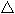 В1ВС и общая высота, проведенная из вершины S к грани параллелограмма ВВ1С1С. Поэтому у них равные объемы. В1ВС и общая высота, проведенная из вершины S к грани параллелограмма ВВ1С1С. Поэтому у них равные объемы. 5. У первой и третьей пирамид тоже равные основания 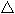 SAB и SAB и 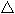 BB1S и совпадающие высоты, проведенные из вершины С к грани параллелограмма АВВ1S. Поэтому у них тоже равные объемы. BB1S и совпадающие высоты, проведенные из вершины С к грани параллелограмма АВВ1S. Поэтому у них тоже равные объемы. Значит, все три пирамиды имеют один и тот же объем. Так как сумма этих объемов равна объему призмы, то объемы пирамид равны Sосн•H/3. | Переливая воду из сосуда – пирамиды в сосуд – призму, учащиеся убеждаются , что ёмкость сосуда – пирамиды примерно в три раза меньше ёмкости сосуда – призмы: Vпир=⅓Vпр =⅓Sосн·H.
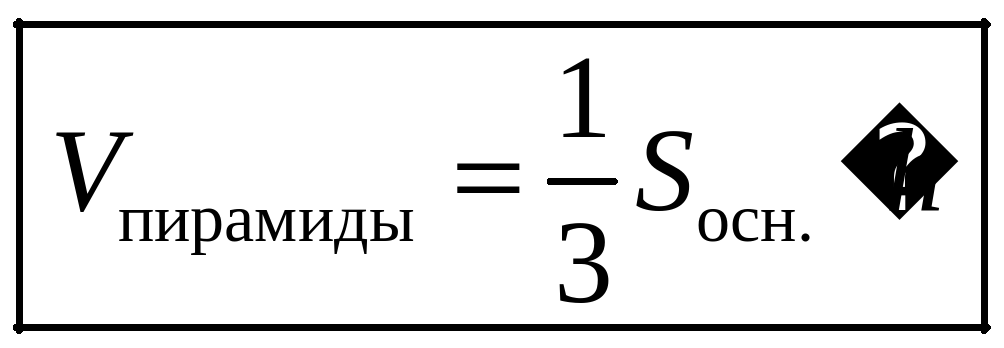
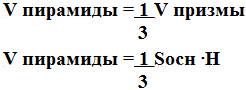
|
|
| Слайд 20 Задача. Найдите объем правильной четырехугольной пирамиды, высота которой равна 12 см, а сторона основания 13 см.
| Решение: V= 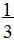 Sосн . H Sосн . H
ABCD – квадрат SABCD = a2 SABCD = 132 = 169 V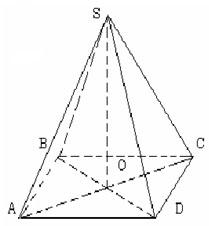 = = 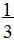 •169 . 12 = 676 (см3) •169 . 12 = 676 (см3) Ответ: Объем правильной четырехугольной пирамиды равен 676 см3 . |
|
| Объем, какой пирамиды нам нужно ещё посмотреть? | Усечённая пирамида |
| Слайд 21 Каким путём получается усечённая пирамида от обычной пирамиды? | Отсечением от неё меньшей пирамиды |
| Можете найти объём усечённой пирамиды?
| У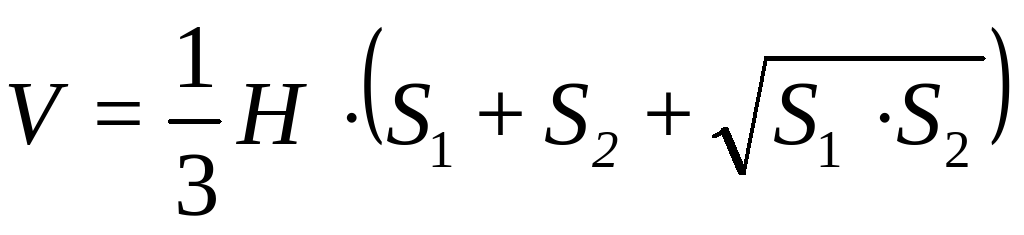 чебник с. 152 чебник с. 152 Следствие 4: объём усеченной пирамиды, высота которого равна H, а площади оснований S и S1 , вычисляется по формуле |
| Какие тела вращения вы знаете? | Цилиндр, конус, усеченный конус, сфера и шар |
| Слайд 22 Давайте выведем с вами формулу для нахождения объема цилиндра. Вспомним обозначения и уже известные нам формулы, которые мы применяли для нахождения элементов цилиндра. | Обозначения: R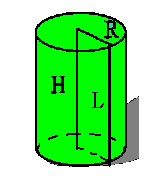 – радиус основания. – радиус основания.
H – высота.
L – образующая.
L= H
V – объем цилиндра.
Sосн = ПR2 |
| Следствие 5: Объем цилиндра равен произведению площади основания на высоту. | V = ПR2H
V = Sосн .H
|
| Слайд 23 Назовите мне фигуру вращения, которую вы видите на данном слайде? | Конус
|
| Давайте вспомним основные обозначения конуса и все уже известные нам формулы, которые мы применяем при решении задач на нахождение элементов конуса.
| Обозначения: R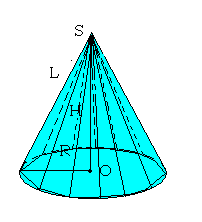 – радиус основания. – радиус основания.
L – образующая конуса.
H – высота.
V – объем. |
|
| Пирамида вписана в конус, если ее основания вписаны в основания конуса и пирамида описана около конуса, если ее основания описаны около оснований конуса. Ясно, что высота любой пирамиды, вписанной в конус или описанной около него равна высоте самого конуса. Так как мы уже знаем с вами, что объем пирамиды равен: V пирамиды = 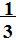 Sосн .H Sосн .H
Тогда и Vконуса = 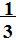 Sосн .H , а в основании конуса лежит круг, то Sосн = ПR2 Sосн .H , а в основании конуса лежит круг, то Sосн = ПR2 Поэтому V= 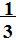 ПR2Н ПR2Н
|
Следствие 6: Объем конуса равен одной трети произведения площади основания на высоту.
|
| Слайд 24 В учебнике на с. 153 рассмотрим вычисление объёма усечённого конуса. | Следствие 7: Объем усечённого конуса, высота которого равна H, а площади оснований равны S и S1 , вычисляется по формуле V = 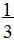 H•(S+S1+S•S1) H•(S+S1+S•S1) |
|
| Слайд 25 Это интересно «Где еще встречается понятие конуса?» (межпредметные связи).
| В геологии существует понятие «конус выноса». Это форма рельефа, образованная скоплением обломочных пород (гальки, гравия, песка), вынесенными горными реками на предгорную равнину или в более плоскую широкую долину. В биологии есть понятие «конус нарастания». Это верхушка побега и корня растений, состоящая из клеток образовательной ткани. «Конусами» называется семейство морских моллюсков подкласса переднежаберных. Раковина коническая (2–16 см), ярко окрашенная. Конусов свыше 500 видов. Живут в тропиках и субтропиках, являются хищниками, имеют ядовитую железу. Укус конусов очень болезнен. Известны смертельные случаи. Раковины используются как украшения, сувениры. В физике встречается понятие «телесный угол». Это конусообразный угол, вырезанный в шаре. Единица измерения телесного угла – 1 стерадиан. 1 стерадиан – это телесный угол, квадрат радиуса которого равен площади части сферы, которую он вырезает. Если в этот угол поместить источник света в 1 канделу (1 свечу), то получим световой поток в 1 люмен. Свет от киноаппарата, прожектора распространяется в виде конуса.
|
| Первичное закрепление | Проверь свои знания: Сформулируйте понятие объема. Сформулируйте основные свойства объемов тел. Назовите единицы измерения объема тел. Назовите формулу для измерения объема:
– прямоугольного параллелепипеда;
– объема куба;
– объем прямой призмы;
– объем пирамиды;
– объем цилиндра
– объем конуса. |
|
| Вопрос: изменится ли объем цилиндра, если радиус его основания увеличить в 2 раза, а высоту уменьшить в 4 раза?
| Решение: V = ПR2H ; V= П(2R)2 .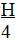 = П4R2. = П4R2. 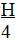 = ПR2. H = ПR2. H
Не изменится |
Основаниями двух пирамид с равными высотами являются четырехугольники с соответственно равными сторонами. Равны ли объемы этих пирамид? | Да, объёмы равны. |
Из каких тел состоит тело, полученное вращением равнобедренной трапеции вокруг большего основания? | Тело вращения будет состоять из трех тел: прямого цилиндра ВСС1В1 и двух равных конусов. |
| Решение задач | Итак, мы с вами изучили объемы некоторых многогранников и тел вращения. Давайте с вами закрепим пройденный материал. Для его закрепления предлагаю вам решить несколько задач. Слайд 26 Задача 1. Три латунных куба с ребрами 3см, 4 см и 5 см переплавлены в один куб. Какое ребро у этого куба?
| Решение: VF=VF1+VF2 +VF3 VF1=33 =27 (см3) VF2=43 =64 (см3) VF3=53 =125 (см3) VF=27+64 +125=216 (см3) VF=а3 а3=216 (см3) а= 6 (см) Ответ: ребро куба равно 6 см. |
| Слайд 27 Задача 2. Найдите объем цилиндра, если радиус его основания равен 6см, а высота 8 см.
| Решение: V = ПR2H
V = П . 62 . 8 = 288П (см3) Ответ: объем цилиндра равен 288 П см3 . |
| Тайм-аут на развитие пространственного воображения | Из каких геометрических фигур состоит это здание? Слайд 28 | Прямоугольный параллелепипед, правильная четырехугольная пирамида…… |
| Слайд 29 Найдите объем пространственного креста, изображенного на рисунке и составленного из единичных кубов. | Ответ: 7
|
| Решение задач | Слайд 30 Задача 3. Авиационная бомба среднего калибра дает при взрыве воронку диаметром 6 м и глубиной 2 м. Какое количество земли (по массе) выбрасывает эта бомба, если 1 м3 земли имеет массу 1650 кг? | Так как диаметр воронки 6 м и глубина 2 м, то радиус полученного конуса составляет 3 м, а высота – 2 м. Найдем объем конуса: 𝑉=,1-3.𝜋,𝑅-2.ℎ=,1-3.∙3,14∙9∙2=18,84 ,м-3. Масса выброшенной земли составляет � � кг� � кг� �31 т. �31 т. Ответ: 31 т |
| Слайд 31 Задача 4. Найдите объем пирамиды, изображенной на рисунке. Ее основанием является многоугольник, соседние стороны которого перпендикулярны, а одно из боковых ребер перпендикулярно плоскости основания и равно 3. | Р ешение: Площадь основания пирамиды равна 27, высота равна 3. Следовательно, объем пирамиды равен 27. Ответ: 27 |
| Решение задач с практическим содержанием | Слайд 32 3 группы – службы: служба экспертов санэпидемстанции служба метеорологов | Дети выбирают старшего эксперта или старшего метеоролога, которые будут объяснять решение задач |
| Служба экспертов санэпидемстанции Содержание задачи: Классное помещение должно быть таким, чтобы на одного учащегося приходилось не менее 6м3 воздуха. Можно ли в кабинете с параметрами а = 8,5 м, b = 6м, с = 3,6м заниматься 30 учащимся, не нарушая санитарной нормы? | Решение: V = аbс или V = Sосн.· h
V = 8,5 · 6 · 3,6 = 183,6(м3)
183,6 : 30 = 6,12(м3) воздуха приходится на одного учащегося. Заключение эксперта: Да, в кабинете можно заниматься 30 учащимся. |
| Служба метеорологов 1 Содержание задачи: Суточное выпадение осадков составило 20 мм. Сколько воды выпало за сутки на треугольную (правильный треугольник) клумбу со стороной 6м? | Решение: Клумба представляет собой геометрическую фигуру – прямую треугольную призму, где h = 20 мм, тогда V = Sосн. · h 1) Sосн. =
2) h = 20 мм, 1 м = 1000 мм, 1мм = 0,001 м, тогда h = 0,02м
3) V = 15,3 · 0,02 = 0,306(м3) = 306(дм3)
4) 1 дм3 = 1 л (воды), тогда 306 дм3 = 306 литров воды Заключение «старшего метеоролога»: За сутки на клумбу выпало 306 литров осадков. |
|
| Служба метеорологов 2 Содержание задачи: По статистике на Земле ежегодно гибнет от разрядов молний 6 человек на 1 000 000 жителей (чаще в южных странах). Громоотвод образует конус безопасности. Будет ли защищен во время грозы дом высотой 6 м, шириной 8 м и длиной 7 м, если высота громоотвода 7 м, а угол между громоотводом и образующей конуса безопасности равен 60 ? ? | Решение: Составим математическую модель задачи. По определению тангенса 𝑡𝑔60°=,7/𝑅-., 𝑅=7: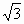 = 4 м�� = 4 м�� ,𝑉-к.=,1-/3.𝜋 16∙7=21𝜋≈117 ,м-3. О бъем дома 𝑉- пар = 8•6•7= 336 � � � Ответ: дом не будет защищен от грозы.
|
| Лабораторно-практическая работа
| Выбрать любой многогранник, записать его название, измерить его параметры и вычислить объем ИЛИ предложенную задачу. | Учащиеся выполняют лабораторно-практическую работу. |
| Сколько м3 воздуха в нашем кабинете? Ширина – Длина – Высота – А мы с вами не нарушаем санитарные нормы? | Вычисляют объем класса. |
|
| Историческая задача На надгробном камне могилы Архимеда в Сиракузах изображен цилиндр с вписанным в него шаром. Это символ открытия формул объёма шара и площади сферы, а также важного вывода, что объём шара, вписанного в цилиндр, в… раз меньше объёма цилиндра и что также относятся поверхности этих тел». Найдите это отношение. Чему равно отношение объёма шара к объёму цилиндра, если их радиусы равны? Делают вывод.
| Р ешение: |
| Итог | Итак, мы заканчиваем с вами знакомство с понятием объем, с некоторыми формулами для нахождения объема многогранников и тел вращения. С остальными формулами мы продолжим знакомство на следующих уроках стереометрии. |
|
| Какие величины повторяются во всех перечисленных формулах? | Высота. |
| Что можете сказать про высоту прямой призмы. | Высота – это боковое ребро. |
| Можно ли параллелепипед назвать призмой? А куб? | Да, это частные случаи призмы. |
| Какие фигуры могут быть в основании призмы и пирамиды? | Треугольник, квадрат, ромб, прямоугольник, параллелограмм, трапеция и др. плоские фигуры |
| Может ли в основании параллелепипеда быть трапеция? | Нет, потому, что параллелепипед – это призма, в основании которой – параллелограмм |
| Домашнее задание | Слайд 33 с. 127, №547 с. 144 № 648 (по рядам б,в,г ), №668 |
|
| Рефлексия | Слайд 34 сегодня я повторил… было интересно… было трудно… я понял, что… теперь я могу… я приобрел… я научился… у меня получилось … я смог… меня удивило… урок дал мне для жизни… |
|
|
| Слайд 35 Спасибо, ребята, вам всем за урок, Пусть все эти знанья будут вам впрок. Пусть вам пригодятся Все знанья объема, Когда вы ремонт Затеваете дома, Когда собираете в путь чемодан, Когда задвигаете в угол диван, Когда наливаете в банку воды, С объемом и площадью будьте на “ты”. Теперь говорю я вам всем “до свидания”, Окончен урок. Благодарю за вниманье.
| Я слышу – я забываю, я вижу – я запоминаю, я делаю – я усваиваю. Китайская мудрость |
1. Выразить величину из формулы: называется формула объема цилиндра, объема конуса. Выразить высоту, радиус, образующую.
2.Что общего у цилиндра и валика для покраски, конуса и картиной Шишкина «Утро в сосновом бору»? (С древне греческого: цилиндр-валик, конус- сосновая шишка).
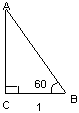
 а рисунке изображены различные геометрические тела. Какие из них являются многогранниками?
а рисунке изображены различные геометрические тела. Какие из них являются многогранниками?






 уб
уб  По модели треугольной призмы вывести формулу для вычисления объёма данной призмы.
По модели треугольной призмы вывести формулу для вычисления объёма данной призмы.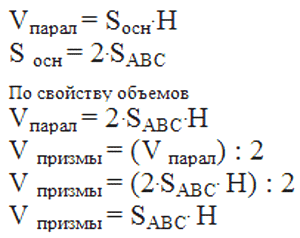

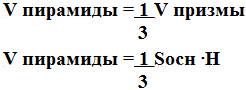


 =
=  – радиус основания.
– радиус основания. – радиус основания.
– радиус основания.















