Муниципальное общеобразовательное автономное учреждение
«Средняя общеобразовательная школа № 40 с углублённым изучением математики имени В.М.Барбазюка» города Оренбурга.
| Согласовано ЗД по УВР ______________ /____________ / ФИО
| Принято Педагогическим советом Протокол №1 от «30» августа2017г.
|
| Утверждено Директор ________ /________/ ФИО Приказ №01-10/121 от«31» августа 2017г.
|
РАБОЧАЯ ПРОГРАММА
по геометрии
8 «А», 8 «Б» классах
( основное общее образование)
Составитель:
учитель математики
Леотина Ирина Валерьевна
Высшая категория
2017-2018
СОДЕРЖАНИЕ
1. Пояснительная записка.
2. Планируемые результаты освоения курса обучающимися.
3. Содержание курса.
4. Тематическое планирование с указанием часов, отводимых на изучение каждой темы
5. Оценочные и методические материалы.
1. Пояснительная записка
Рабочая программа курса геометрии предназначена для изучения в 8 классе и составлена на основании следующих документов:
Федеральный компонент образовательного стандарта основного общего образования, утверждённый приказом Министерства образо вания Российской Федерации от 5 марта 2004 года № 1089 «Об утверждении федерального компонента государственного образовательного стандарта начального общего, основного общего и среднего (полного) общего образования» (с изменениями и дополнениями) – далее стандарт 2004 г.
С учетом авторской программы: В. Ф. Бутузов «Геометрия. Рабочая программа к учебнику Л. С. Атанасяна и др.. 7-9 классы»- М.: Просвещение, 2011.
Основная образовательная программа основного общего образования МОАУ «СОШ № 40».
Локальный нормативный акт «Положение о рабочей программе учителя-предметника».
Изучение геометрии на уровне основного общего образования направлено на достижение следующих целей:
-овладение системой математических знаний и умений, необходимых в практической деятельности, продолжения образования;
-приобретение опыта планирования и осуществления алгоритмической деятельности;
-освоение навыков и умений проведения доказательств, обоснования выбора решений;
-приобретение умений ясного и точного изложения мыслей;
-развить пространственные представления и умения, помочь освоить основные факты и методы планиметрии.
Основные формы организации учебных занятий: урок первичного предъявления новых знаний; урок формирования первоначальных предметных навыков, овладения новыми предметными умениями; урок применения предметных знаний; урок обобщения и систематизации предметных знаний; урок повторения предметных знаний; контрольный урок; комбинированный урок; урок - практическая работа.
При реализации рабочей программы по геометрии используются следующие основные виды деятельности: словесные (рассказ, беседа, лекция с элементами беседы); наглядные (демонстрация плакатов, учебных видео роликов, электронных презентаций); эвристические (саморазвитие обучающихся, активная познавательная деятельность); практические (решение теоретических и практических задач); участвовать в определении проблемы и постановке целей урока; планировать свою работу на уроке; осуществлять самооценку и взаимооценку; осуществлять рефлексию собственной деятельности на уроке.
В программе предложен авторский подход в части структурирования учебного материала, определения последовательности его изучения, путей формирования системы знаний, умений и способов деятельности, развития, воспитания и социализации учащихся.
В соответствии с учебным планом МОАУ «Средняя общеобразовательная школа № 40 с углублённым изучением математики имени
В. М. Барбазюка» города Оренбург на 2017-2018 учебный год рабочая программа по геометрии рассчитана на 35 учебных недель: 2 часа в неделю, 70 часов за год. Из них: Повторение курса 7 класса – 2 часа; Контрольных работ – 5 часов; Повторение курса 8 класса – 4 часа.
2. ПЛАНИРУЕМЫЕ РЕЗУЛЬТАТЫ ОСВОЕНИЯ КУРСА ОБУЧАЮЩИМИСЯ
В результате изучения математики ученик должен:
знать/понимать :
--------------------------------
Помимо указанных в данном разделе знаний, в требования к уровню подготовки включаются также знания, необходимые для освоения перечисленных ниже умений.
- существо понятия математического доказательства; примеры доказательств;
- существо понятия алгоритма; примеры алгоритмов;
- как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
- как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
- как потребности практики привели математическую науку к необходимости расширения понятия числа;
- вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;
- каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;
- смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации.
Уметь:
- пользоваться языком геометрии для описания предметов окружающего мира;
- распознавать геометрические фигуры, различать их взаимное расположение;
- изображать геометрические фигуры; выполнять чертежи по условию задач; осуществлять преобразования фигур;
- распознавать на чертежах, моделях и в окружающей обстановке основные пространственные тела, изображать их;
- в простейших случаях строить сечения и развертки пространственных тел;
- проводить операции над векторами, вычислять длину и координаты вектора, угол между векторами;
- вычислять значения геометрических величин (длин, углов, площадей, объемов), в том числе: для углов от 0 до 180° определять значения тригонометрических функций по заданным значениям углов; находить значения тригонометрических функций по значению одной из них, находить стороны, углы и площади треугольников, длины ломаных, дуг окружности, площадей основных геометрических фигур и фигур, составленных из них;
- решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический и тригонометрический аппарат, идеи симметрии;
- проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования;
- решать простейшие планиметрические задачи в пространстве;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
- описания реальных ситуаций на языке геометрии;
- расчетов, включающих простейшие тригонометрические формулы;
- решения геометрических задач с использованием тригонометрии;
- решения практических задач, связанных с нахождением геометрических величин (используя при необходимости справочники и технические средства);
- построений геометрическими инструментами (линейка, угольник, циркуль, транспортир).
3.Содержание курса
Геометрия
Теоремы о параллельности и перпендикулярности прямых.
Равнобедренные и равносторонние треугольники; свойства и признаки равнобедренного треугольника.
Признаки равенства треугольников. Зависимость между величинами сторон и углов треугольника.
Многоугольники.
Окружность и круг.
Высота, медиана, биссектриса, средняя линия треугольника.
Теорема Фалеса. Подобие треугольников; коэффициент подобия. Признаки подобия треугольников. Пропорциональные отрезки в прямоугольном треугольнике. Практическое приложение подобия треугольников.
Теорема Пифагора. Теорема, обратная теореме Пифагора. Синус, косинус, тангенс, котангенс острого угла прямоугольного треугольника и углов от 0° до 180°; приведение к острому углу. Основное тригонометрическое тождество. Формулы, связывающие синус, косинус, тангенс, котангенс одного и того же угла.
Замечательные точки треугольника: точки пересечения серединных перпендикуляров, биссектрис, медиан.
Четырехугольник. Параллелограмм, его свойства и признаки. Прямоугольник, квадрат, ромб, их свойства и признаки. Трапеция, равнобедренная трапеция.
Многоугольники. Выпуклые многоугольники. Сумма углов выпуклого многоугольника. Окружность и круг.
Центр, радиус, диаметр. Дуга, хорда. Центральный, вписанный угол; величина вписанного угла. Взаимное расположение прямой и окружности. Касательная и секущая к окружности; равенство касательных, проведенных из одной точки. МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В ОКРУЖНОСТИ: СВОЙСТВА СЕКУЩИХ, КАСАТЕЛЬНЫХ, ХОРД.
Окружность, вписанная в треугольник, и окружность, описанная около треугольника. ВПИСАННЫЕ И ОПИСАННЫЕ ЧЕТЫРЕХУГОЛЬНИКИ. Градусная мера угла, соответствие между величиной угла и длиной дуги окружности.
Понятие о площади плоских фигур. Равносоставленные и равновеликие фигуры.
Площадь прямоугольника. Площадь параллелограмма, треугольника и трапеции (основные формулы). Площадь ромба. ФОРМУЛА ГЕРОНА.
Связь между площадями подобных фигур.
Геометрические преобразования
СИММЕТРИЯ ФИГУР. ОСЕВАЯ СИММЕТРИЯ И ЦЕНТРАЛЬНАЯ СИММЕТРИЯ. ПОДОБИЕ ФИГУР.
4.Тематическое планирование с указанием часов, отводимых на изучение каждой темы.
| Номер урока |
Название темы |
Основные виды деятельности | Количество часов | Сроки |
| По плану | Фактическое проведение |
| 1 | Повторение курса 7 класса. Теоремы о параллельности и перпендикулярности прямых. Равнобедренные и равносторонние треугольники; свойства и признаки равнобедренного треугольника. | Учащиеся должны знать начальные понятия геометрии, определения смежных и вертикальных углов, равнобедренного треугольника и его элементов, свойство медианы равнобедренного треугольника, признаки равенства треугольников, определение параллельных прямых, признаки и свойства параллельных прямых, теорему о сумме углов треугольника; | 1 | 02.09 |
|
| 2 | Повторение курса 7 класса. Признаки равенства треугольников. Зависимость между величинами сторон и углов треугольника. | Учащиеся должны уметь решать наиболее типичные задачи из курса геометрии 7 класса. | 1 | 06.09 |
|
| 3 | Многоугольники. Выпуклые многоугольники. | Объяснять, что такое многоугольник, его вершины, смежные стороны, диагонали, изображать и распознавать многоугольники на чертежах; показывать элементы многоугольника, его внутреннюю и внешнюю области; формулировать определение выпуклого многоугольника; изображать и распознавать выпуклые и невыпуклые многоугольники; формулировать и доказывать утверждение о сумме углов выпуклого многоугольника; объяснять какие стороны (вершины) четырехугольника называются противоположными | 1 | 09.09 |
|
| 4 | Сумма углов выпуклого многоугольника. Четырехугольник. | Формулировать и доказывать утверждение о сумме углов выпуклого многоугольника; объяснять какие стороны (вершины) четырехугольника называются противоположными | 1 | 13.09 |
|
| 5 | Параллелограмм, его свойства и признаки. | Формулировать определения параллелограмма, трапеции, равнобедренной и прямоугольной трапеций, прямоугольника, ромба, квадрата; изображать и распознавать эти четырехугольники; формулировать и доказывать утверждения об их свойствах и признаках; решать задачи на вычисление, доказательство и построение, связанные с этими видами четырехугольников | 1 | 16.09 |
|
| 6 | Параллелограмм, его свойства и признаки. | 1 | 20.09 |
|
| 7 | Параллелограмм, его свойства и признаки. | 1 | 23.09 |
|
| 8 | Трапеция, равнобедренная трапеция. | 1 | 27.09 |
|
| 9 | Трапеция, равнобедренная трапеция. | 1 | 30.09 |
|
| 10 | Теорема Фалеса. | 1 | 04.10 |
|
| 11 | Прямоугольник, квадрат, ромб, их свойства и признаки. | 1 | 07.10 |
|
| 12 | Прямоугольник, квадрат, ромб, их свойства и признаки. | 1 | 11.10 |
|
| 13 | Прямоугольник, квадрат, ромб, их свойства и признаки. | 1 | 14.10 |
|
| 14 | Прямоугольник, квадрат, ромб, их свойства и признаки. | 1 | 18.10 |
|
| 15 | Геометрические преобразования. СИММЕТРИЯ ФИГУР. ОСЕВАЯ СИММЕТРИЯ И ЦЕНТРАЛЬНАЯ СИММЕТРИЯ. | Объяснять, какие две точки называются симметричными относительно прямой(точки), в каком случае фигура называется симметричной относительно прямой (точки) и что такое ось (центр) симметрии; приводить примеры фигур, обладающих осевой (центральной) симметрией, а также примеры осевой и центральной симметрии в окружающей нас обстановке. | 1 | 21.10 |
|
| 16 | Контрольная работа №1 по теме «Четырёхугольники». |
| 1 | 25.10 |
|
| 17 | Понятие о площади плоских фигур. Равносоставленные и равновеликие фигуры. | Объяснять, как производится измерение площадей многоугольников; формулировать основные свойства площадей и выводить с их помощью формулы площадей прямоугольника, параллелограмма, треугольника, трапеции; | 1 | 28.10 |
|
| 18 | Площадь прямоугольника. | 1 | 2 ч. 08.11 |
|
| 19 | Площадь параллелограмма, треугольника и трапеции (основные формулы) | 1 | 11.11 |
|
| 20 | Площадь параллелограмма, треугольника и трапеции (основные формулы). | 1 | 15.11 |
|
| 21 | Площадь параллелограмма, треугольника и трапеции (основные формулы). | 1 | 18.11 |
|
| 22 | Площадь параллелограмма, треугольника и трапеции (основные формулы). | 1 | 22.11 |
|
| 23 | Площадь ромба. | 1 | 25.11 |
|
| 24 | Площадь ромба. | 1 | 29.11 |
|
| 25 | Теорема Пифагора. | Формулировать и доказывать теорему об отношении площадей треугольников, имеющих по равному углу; формулировать и доказывать теорему Пифагора и обратную ей | 1 | 02.12 |
|
| 26 | Теорема, обратная теореме Пифагора. | Формулировать и доказывать теорему об отношении площадей треугольников, имеющих по равному углу; формулировать и доказывать теорему Пифагора и обратную ей | 1 | 06.12 |
|
| 27 | Теорема, обратная теореме Пифагора. | Формулировать и доказывать теорему об отношении площадей треугольников, имеющих по равному углу; формулировать и доказывать теорему Пифагора и обратную ей | 1 | 09.12 |
|
| 28 | ФОРМУЛА ГЕРОНА. | Выводить формулу Герона для площади треугольника; решать задачи на вычисление и доказательство, связанные с формулами площадей и теоремой Пифагора | 1 | 13.12 |
|
| 29 | ФОРМУЛА ГЕРОНА. | Выводить формулу Герона для площади треугольника; решать задачи на вычисление и доказательство, связанные с формулами площадей и теоремой Пифагора | 1 | 16.12 |
|
| 30 | Контрольная работа №2 по теме «Площадь». |
| 1 | 20.12 |
|
| 31 | Подобие треугольников; коэффициент подобия. ПОДОБИЕ ФИГУР. | Объяснять понятие пропорциональности отрезков; формулировать определения подобных треугольников и коэффициента подобия; | 1 | 23.12 |
|
| 32 | Связь между площадями подобных фигур. | Формулировать и доказывать теоремы: об отношении площадей подобных треугольников | 1 | 27.12 |
|
| 33 | Признаки подобия треугольников. | Формулировать и доказывать теоремы о признаках подобия треугольников, о пересечении медиан треугольника, о пропорциональных отрезках в прямоугольном треугольнике; объяснять, что такое метод подобия в задачах на построение, и приводить примеры применения этого метода; объяснять, как можно использовать свойства подобных треугольников в измерительных работах на местности; объяснять, как ввести понятие подобия для произвольных фигур; | 1 | 3 ч. 13.01 |
|
| 34 | Признаки подобия треугольников. | 1 | 17.01 |
|
| 35 | Признаки подобия треугольников. | 1 | 20.01 |
|
| 36 | Признаки подобия треугольников. | 1 | 24.01 |
|
| 37 | Признаки подобия треугольников. | 1 | 27.01 |
|
| 38 | Контрольная работа №3 по теме «Признаки подобия треугольников». |
| 1 | 31.01 |
|
| 39 | Средняя линия треугольника. | Формулировать и доказывать теорему о средней линии треугольника | 1 | 03.02 |
|
| 40 | Средняя линия треугольника. | Формулировать и доказывать теорему о средней линии треугольника | 1 | 07.02 |
|
| 41 | Пропорциональные отрезки в прямоугольном треугольнике. | Решать задачи, связанные с подобием треугольников, для вычисления значений тригонометрических функций использовать компьютерные программы. | 1 | 10.02 |
|
| 42 | Пропорциональные отрезки в прямоугольном треугольнике. | Решать задачи, связанные с подобием треугольников, для вычисления значений тригонометрических функций использовать компьютерные программы. | 1 | 14.02 |
|
| 43 | Практическое приложение подобия треугольников. | Решать задачи, связанные с подобием треугольников, для вычисления значений тригонометрических функций использовать компьютерные программы. | 1 | 17.02 |
|
| 44 | Практическое приложение подобия треугольников. | Решать задачи, связанные с подобием треугольников, для вычисления значений тригонометрических функций использовать компьютерные программы. | 1 | 21.02 |
|
| 45 | Практическое приложение подобия треугольников. | Решать задачи, связанные с подобием треугольников, для вычисления значений тригонометрических функций использовать компьютерные программы. | 1 | 24.02 |
|
| 46 | Синус, косинус, тангенс, котангенс острого угла прямоугольного треугольника и углов от 0° до 180°; приведение к острому углу. Основное тригонометрическое тождество. | Формулировать определение и иллюстрировать понятие синуса, косинуса и тангенса острого угла прямоугольного треугольника; выводить основное тригонометрическое тождество и значения синуса, косинуса и тангенса для углов 30°, 45°, 60°; | 1 | 28.02 |
|
| 47 | Синус, косинус, тангенс, котангенс острого угла прямоугольного треугольника и углов от 0° до 180°; приведение к острому углу. Основное тригонометрическое тождество. | Формулировать определение и иллюстрировать понятие синуса, косинуса и тангенса острого угла прямоугольного треугольника; выводить основное тригонометрическое тождество и значения синуса, косинуса и тангенса для углов 30°, 45°, 60°; | 1 | 03.03 |
|
| 48 | Формулы, связывающие синус, косинус, тангенс, котангенс одного и того же угла. | Формулировать определение и иллюстрировать понятие синуса, косинуса и тангенса острого угла прямоугольного треугольника; выводить основное тригонометрическое тождество и значения синуса, косинуса и тангенса для углов 30°, 45°, 60°; | 1 | 07.03 |
|
| 49 | Формулы, связывающие синус, косинус, тангенс, котангенс одного и того же угла. | Формулировать определение и иллюстрировать понятие синуса, косинуса и тангенса острого угла прямоугольного треугольника; выводить основное тригонометрическое тождество и значения синуса, косинуса и тангенса для углов 30°, 45°, 60°; | 1 | 10.03 |
|
| 50 | Контрольная работа №4 по теме «Средняя линия треугольника. Синус, косинус, тангенс, котангенс острого угла прямоугольного треугольника и углов от 0° до 180°». |
| 1 | 14.03 |
|
| 51 | Окружность и круг. Центр, радиус, диаметр. Дуга, хорда. Взаимное расположение прямой и окружности. | Исследовать взаимное расположение прямой и окружности; формулировать определение касательной к окружности; формулировать и доказывать теоремы: о свойстве касательной, о признаке касательной, об отрезках касательных, проведенных из одной точки; формулировать понятие центрального угла и градусной меры дуги окружности; формулировать и доказывать теоремы: о вписанном угле, о произведении пересекающихся хорд; формулировать и доказывать теоремы, связанные с замечательными точками треугольника: о биссектрисе угла и, как следствие, о пересечении биссектрис треугольника; о серединном перпендикуляре к отрезку и, как следствие, о пересечении серединных перпендикуляров к сторонам треугольника; о пересечении высот треугольника; формулировать определения окружностей, вписанных в многоугольник и описанной около многоугольника; формулировать и доказывать теоремы: об окружности, вписанной в треугольник; об окружности, описанной около треугольника; о свойстве сторон описанного четырехугольника; о свойстве углов вписанного четырехугольника; решать задачи на вычисление, доказательство и построение, связанные с окружностью, вписанными и описанными треугольниками и четырехугольниками; исследовать свойства конфигураций, связанных с окружностью, с помощью компьютерных программ. | 1 | 17.03 |
|
| 52 | Касательная и секущая к окружности; равенство касательных, проведенных из одной точки. | 1 | 21.03 |
|
| 53 | Касательная и секущая к окружности; равенство касательных, проведенных из одной точки. | 1 | 4 ч. 04.04 |
|
| 54 | Градусная мера угла, соответствие между величиной угла и длиной дуги окружности. | 1 | 07.04 |
|
| 55 | Центральный, вписанный угол; величина вписанного угла. | 1 | 11.04 |
|
| 56 | МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В ОКРУЖНОСТИ: СВОЙСТВА СЕКУЩИХ, КАСАТЕЛЬНЫХ, ХОРД. | 1 | 14.04 |
|
| 57 | Замечательные точки треугольника: точки пересечения серединных перпендикуляров, биссектрис, медиан. | 1 | 18.04 |
|
| 58 | Замечательные точки треугольника: точки пересечения серединных перпендикуляров, биссектрис, медиан. | 1 | 21.04 |
|
| 59 | Замечательные точки треугольника: точки пересечения серединных перпендикуляров, биссектрис, медиан. | 1 | 25.04 |
|
| 60 | Замечательные точки треугольника: точки пересечения серединных перпендикуляров, биссектрис, медиан. | 1 | 28.04 |
|
| 61 | Окружность, вписанная в треугольник, и окружность, описанная около треугольника. | 1 | 02.05 |
|
| 62 | Окружность, вписанная в треугольник, и окружность, описанная около треугольника. | 1 | 05.05 |
|
| 63 | ВПИСАННЫЕ И ОПИСАННЫЕ ЧЕТЫРЕХУГОЛЬНИКИ. | 1 | 09.05 |
|
| 64 | ВПИСАННЫЕ И ОПИСАННЫЕ ЧЕТЫРЕХУГОЛЬНИКИ. | 1 | 12.05 |
|
| 65 | ВПИСАННЫЕ И ОПИСАННЫЕ ЧЕТЫРЕХУГОЛЬНИКИ. | 1 | 16.05 |
|
| 66 | Контрольная работа №5 по теме «Окружность». |
| 1 | 19.05 |
|
| 67 | Повторение курса 8 класса. Четырехугольник. Площадь. | Повторить и систематизировать основные теоретические факты курса геометрии 8 класса | 1 | 23.05 |
|
| 68 | Повторение курса 8 класса. Признаки подобия треугольников. Окружность. | Повторить и систематизировать основные теоретические факты курса геометрии 8 класса | 1 | 26.05 |
|
| 69 | Повторение курса 8 класса. Синус, косинус, тангенс, котангенс острого угла прямоугольного треугольника и углов от 0° до 180°; приведение к острому углу. Основное тригонометрическое тождество. | Повторить и систематизировать основные теоретические факты курса геометрии 8 класса | 1 | 30.05 |
|
| 70 | Итоговая контрольная работа |
| 1 | 31.05 |
|
5. ОЦЕНОЧНЫЕ И МЕТОДИЧЕСКИЕ МАТЕРИАЛЫ.
Контрольная работа №1по теме: «Четырехугольники».
Вариант 1
А1. Периметр параллелограмма ABCD равен 80 см. 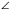 А = 30о, а перпендикуляр ВН к прямой АD равен 7,5 см. Найдите стороны параллелограмма
А = 30о, а перпендикуляр ВН к прямой АD равен 7,5 см. Найдите стороны параллелограмма
А2. Докажите, что у равнобедренной трапеции углы при основании равны.
А3. Постройте ромб по двум диагоналям. Сколько осей симметрии у ромба?
________________________________________________
В1. Точки Р, К, L, M – середины сторон ромба АВСD. Докажите, что четырехугольник РКLM – прямоугольник.
Вариант 2
А1. Диагональ квадрата равна 4 см. Сторона его равна диагонали другого квадрата. Найдите сторону последнего.
А2. Докажите, что середины сторон прямоугольника являются вершинами ромба.
А3. Постройте квадрат по диагонали. Сколько осей симметрии имеет квадрат?
________________________________________________
В1. В трапеции АВСD меньшее основание ВС равно 4 см. Через вершину В проведена прямая, параллельная стороне СD. Периметр образовавшегося треугольника равен 12 см. Найдите периметр трапеции.
Контрольная работа №2 «Площади фигур».
Вариант 1
А1. В прямоугольнике ABCD АВ = 24 см, АС = 25 см. Найдите площадь прямоугольника.
А2. Найдите площадь прямоугольного треугольника, если гипотенуза его равна 40 см, а острый угол равен 60о.
А3. Найдите площадь ромба, если его диагонали равны 14 и 6 см.
А4. Найдите площадь равнобедренной трапеции, у которой высота равна 16 см, а диагонали взаимно перпендикулярны.
____________________________________________________
В1. Середины оснований трапеции соединены отрезком.
Докажите, что полученные две трапеции равновелики.
Вариант 2
А1. В ромбе ABCD АВ = 10 см, меньшая диагональ АС = 12 см. Найдите площадь ромба.
А2. Найдите площадь равнобедренного треугольника, если его боковая сторона равна 6 см, а угол при вершине равен 60о.
А3. Найдите площадь прямоугольника, если его диагональ равна 13 см, а одна из сторон 5 см.
А4. Найдите площадь равнобедренной трапеции, у которой высота равна 16 см, а диагонали взаимно перпендикулярны.
____________________________________________________
В1. Докажите, что медиана треугольника разбивает его на два треугольника одинаковой площади.
Контрольная работа №3 по теме «Признаки подобия треугольников».
Вариант 1
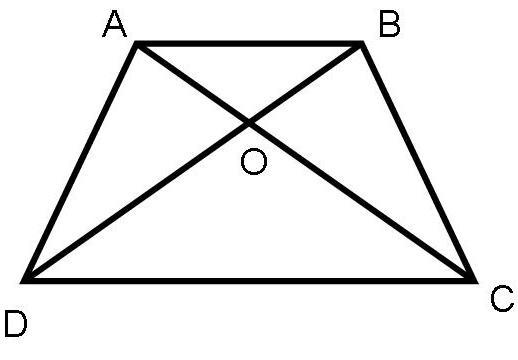
А1. На рисунке АВ || CD.
а) Докажите, что АО : ОС = ВО : OD.
б) Найдите АВ, если OD = 15 см, ОВ = 9 см,
CD = 25 см.
А2. Найдите отношение площадей треугольников ABC и KMN, если АВ = 8 см, ВС = 12 см, АС = 16 см, КМ = 10 см, MN = 15 см, NK = 20 см.
__________________________________________
В1. Докажите, что в подобных треугольниках отношение двух сходственных сторон равно отношению двух сходственных высот.
Вариант 2
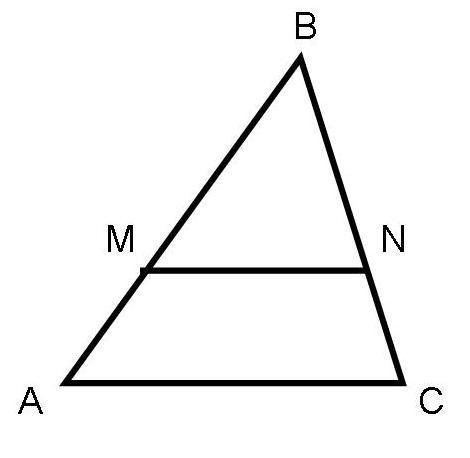
А1. На рисунке MN || АС.
а) Докажите, что 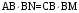 .
.
б) Найдите MN, если AM = 6 см, ВМ = 8 см,
АС = 21 см.
А2. Даны стороны треугольников PКМ и ABC:
PК = 16 см, КМ = 20 см, РМ = 28 см и АВ = 12 см,
ВС = 15 см, АС = 21 см. Найдите отношение площадей этих треугольников.
______________________________________
В1. Докажите, что в подобных треугольниках отношение двух сходственных сторон равно отношению двух сходственных биссектрис.
Контрольная работа №4 по теме «Средняя линия треугольника. Синус, косинус, тангенс, котангенс острого угла прямоугольного треугольника и углов от 0° до 180°».
Вариант 1
А1. Отрезки АВ и СМ пересекаются в точке О так, что АС || ВМ. Найдите длину отрезка СМ, если АО=12 см, ОВ=3 см, СО=8 см.
А2. В треугольнике АВС точка К принадлежит стороне АВ, а точка Р – стороне АС. Отрезок КР|| BC. Найдите периметр треугольника АКР, если АВ=9 см, ВС=12 см, АС=15 см и АК : КВ=2:1.
А3. В треугольнике АВС угол С=900. АС=15см, ВС=8 см. Найдите 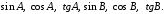
__________________________________________
В1. Между пунктами А и В находится болото. Чтобы найти расстояние между А и В, отметили вне болота произвольную точку С, измерили расстояние АС = 600 м и ВС = 400 м, а также  АСВ = 62°.
АСВ = 62°.
Начертите план в масштабе 1 : 10 000 и найдите по нему расстояние между пунктами А и В.
Вариант 2
А1. Отрезки АВ и СМ пересекаются в точке О так, что АС || ВМ. Найдите длину отрезка СМ, если АС=15 см, ВМ=3 см, СО=10 см.
А2. В треугольнике АВС точка К принадлежит стороне АВ, а точка Р – стороне АС. Отрезок КР|| BC. Найдите периметр треугольника АКР, если АВ=16 см, ВС=8 см, АС=15 см и АК =4 см.
А3. В треугольнике АВС угол С=900. АС=4 см, АВ=5 см. Найдите 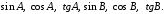
______________________________________
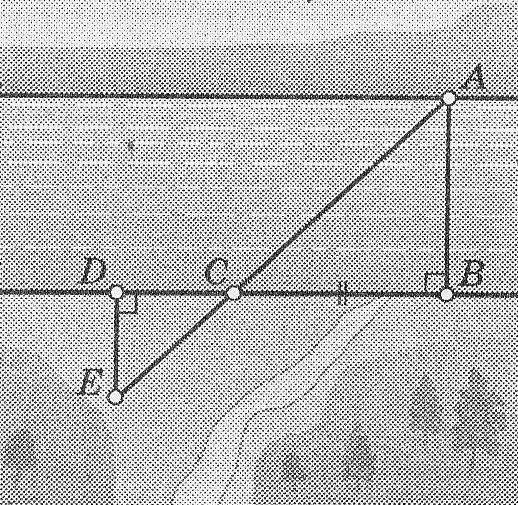
В1. На рисунке показано, как можно определить ширину реки АВ, построив на местности подобные треугольники. Обоснуйте: какие построения выполнены; чем мы пользуемся для определения ширины реки? Выполните необходимые измерения и определите ширину реки
(масштаб рисунка 1 : 1000).
Контрольная работа №5по теме «Окружность».
Вариант 1
А1. Из точки данной окружности проведены диаметр и хорда, равная радиусу. Найдите угол между ними.
А2. Хорда АВ стягивает дугу, равную 125о, а хорда АС – дугу в 52о. Найдите угол ВАС
А3. Постройте окружность, описанную около тупоугольного треугольника.
_____________________________________________
В1. Основание равнобедренного треугольника равно 18 см, а боковая сторона равна 15 см. Найдите радиусы вписанной в треугольник и описанной около треугольника окружностей.
Вариант 2
А1. Через точку данной окружности проведены касательная и хорда, равная радиусу. Найдите угол между ними.
А2. Хорда АВ стягивает дугу, равную 75о, а хорда АС – дугу в 112о. Найдите угол ВАС
А3. Постройте окружность, вписанную в данный треугольник.
_____________________________________________
В1. Высота, проведенная к основанию равнобедренного треугольника, равна 9 см, а само основание равно 24 см. Найдите радиусы вписанной в треугольник и описанной около треугольника окружностей.
Учебно - методический комплект:
1. Программа Л.С.Атанасян, В.Ф.Бутусов, С.Б.Кадомцев и др. Геометрия 7-9 классы. - М.: Просвещение, 2009;
2. С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. Геометрия 7-9 кл./ – 16-е изд. – М.: Просвещение, 2011.
Литература для учителя:
1. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. Учебник Геометрия 7-9 классы М.: Просвещение, 2011.
2. Гаврилова Н.Ф. Поурочные разработки по геометрии 8 класс. - М.: «ВАКО», 2005.
3. Ершова А.П. Самостоятельные и контрольные работы по геометрии для 8 класса. Разноуровневые дидактические материалы. - М: Илекса, 2005.
4. Зив Б.Г. Дидактические материалы по геометрии.- М.: Просвещение, 2008.
Дополнительная литература:
1. Азевич А.И. Задачи по геометрии. 7 – 9 классы: Дидактические материалы и контрольные работы. – М.: Школьная пресса, 2006.
2. Виленкина П.Я. Сборник задач по геометрии для 6 – 8 классов. Пособие для учителей. Изд.2, переработ.и доп. М., «Просвещение», 2005.
3. Единый государственный экзамен: математика: сб.заданий / М.О. Денищева. Г.К. Безрукова, Е.М. Байченко и др./ - 2-е изд. – М.: Просвещение, 2006.
4. Журнал «Математика в школе»
5. Математика. 5 – 11 классы: нетрадиционные формы организации тематического контроля на уроках/авт.-сост. М.Е. Козина, О.М. Фадеева. – Волгоград: Учитель, 2006.
6. Прасолов В.В. задачи по планиметрии, ч. I. – М.: Наука. Гл.ред.физ.-мат.лит., 2005.
7. Проверочные задания по математике для учащихся 5 – 8 и 10 классов средней школы: Пособие для учителя / Л.М. Буланова, Ю.П. Дудницын, О.Н. Доброва и др. – М.: Просвещение, 2003.
8. Рубежный контроль по математике. 6 5 – 9 классы /Р. Изместьева. – М.: Чистые пруды, 2006.
9. Саврасова С.М., Ястребинецкий Г.А. Упражнения по планиметрии на готовых чертежах: Пособие для учителя. – М.: Просвещение, 2002
10. Тесты. Математика. 5 – 11 кл. – М.: ООО «Агенство» «КРПА «Олимп»: ООО «Издательство АСТ», 2007.
Литература для учащихся
1.Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. Учебник Геометрия 7-9 классы. - М.: Просвещение, 2011.
2. Атанасян Л.С. Рабочая тетрадь по геометрии 8 класс.- М.: Просвещение, 2009.
3. Зив Б.Г. Дидактические материалы по геометрии. - М.: Просвещение, 2008.
Медиаресурсы:
1. http://festival.1september.ru
2. http://www.ed.gov.ru/
3. http://www.edu/ru/
4. http://edu.secna.ru/main/
5. http://mega.km.ru
6. http://www.encyclopedia.ru
7. http://le-savchen.ucoz.ru
8.http://le-savchen.ucoz.ru
9. Электронный диск СD Геометрия 7-9. Карточки, издательство Учитель, 2009.
Технические средства обучения:
Компьютер, ноутбук, мультимедийный проектор, демонстрационный экран.
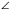 А = 30о, а перпендикуляр ВН к прямой А
А = 30о, а перпендикуляр ВН к прямой А

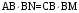 .
.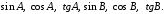
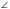 АСВ = 62°.
АСВ = 62°. 
















