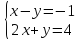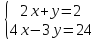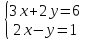Открытый урок по теме "Система двух уравнений с двумя неизвестными"

Методическое объединение учителей математики.

Место проведения: Муниципальное общеобразовательное учреждение

« Тираспольская средняя школа № 8»

Дата проведения: 05.12.2014 год

План проведения:

Тема: Системы двух уравнений с двумя неизвестными

Тип урока: Комбинированный урок: урок закрепления и развития знаний, умений, навыков; повторения; проверки знаний; изучения нового исторического материала.

Цель урока: Содействовать обобщению и систематизации знаний учащихся по теме “Решение систем уравнений”; продолжить закрепление следующих умений: решение систем уравнений графическим способом, способом подстановки, способом сложения .

Развитие познавательного интереса, совершенствовать навыки решения систем уравнений; Обобщить знания основного программного материала.

Ход урока

1. Организация начала урока (психологический настрой учащихся). Сообщаются: тема урока и его задачи.

2. Актуализация опорных знаний:

1) Уравнение и его свойства Определение

Уравнение – это равенство, содержащее одну или несколько переменных

Из истории уравнений Уравнение с двумя неизвестными выражает зависимость между двумя величинами , имеет бесчисленное множество реше -ний и является неопределенным.

Решением таких уравнений занимались в древности китайцы, греки и индийцы.

В «Арифметике» Диофанта приведено много задач, решаемых им с помощью неопределенных уравнений.

2)Решением уравнения с двумя неизвестными х и у

• называется упорядоченная пара чисел ( х ; у ), при подстановке которых в это уравнение получается называется упорядоченная пара чисел ( х ; у ), при подстановке которых в это уравнение получается верное числовое равенство. верное числовое равенство.

3)Система уравнений и её решение

Определение

Системой двух линейных уравнений с двумя неизвестными называются два уравнения, объединенные фигурной скобкой.

Фигурная скобка означает, что эти уравнения должны быть решены одновременно.

В общем виде систему двух линейных уравнений с двумя неизвестными записывают так

а1 х + b1 y = c1,

а2 х + b2 y = c2

4)Из истории систем уравнений

Задачи на составление и решение систем уравнений встречаются в вавилонских и египетских текстах II тысячелетия до н. э., в трудах древнегреческих, китайских и индийских ученых.

Нижние индексы при буква впервые употребил в 1675 г.немецкий математик Лейбниц

5)Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство

Решить систему уравнений - это значит найти все её решения или установить, что их нет

6) Способы решения систем: графический способ, способ подстановки, способ сложения

III Закрепление изученного.

7) Способ подстановки

• Самым первым, самым главным
  Этот способ назову
  Применяет его каждый 
  Изучить вам помогу.

• По две буквы в уравненьях
  Вам их следует найти
  Но для этого смекалку 
  Мой дружочек примени.

• Из любого уравненья
  Букву вырази одну
  И в другое, без сомненья, 
  Подстановку совершу.

• Получу я уравненье - 
  Неизвестное одно,
  Я найду его решенье, 
  То - какое-то число.

• И число я в уравненье
  Вместо буквы запишу
  Чтоб найти вторую букву
  Вычисленья завершу.

• Получу ответ: икс, игрек
  И система решена
  В круглых скобках пара чисел
  Запись эта так важна.

8) Задание. Заполните пропуски.

9) Графический способ

• Благодаря методу координат, созданному в 17 веке Ферма и Декартом, стало возможным геометрическое решение уравнений систем. Так называемый графический метод решения состоит в построении абсциссы х и ординаты у точки пересечения двух соответствующих прямых.

10) Работа в группах. Решить уравнения графическим способом.

11) Способ сложения

• Запишу два уравненья,
  Неизвестных тоже два.
  Применю способ сложенья
  Им владею я сполна
  Я домножу уравненья
  На число непросто так
  Чтобы выполнить сложенье,
  Между ними ставим знак.
  В левой части икс и игрек
  Аккуратно я сложу
  Получу одну лишь букву,
  Её корнем назову.
  Эту букву я подставлю
  В уравненье номер два
  И вторую найду букву,
  Всё, система решена.

• Нет способа верней.

12) Решите задачу

Сумма двух чисел равна 12, а их разность равна 2. Найдите эти числа.

Решение.

1. Пусть х и у - искомые числа.

2. По условию задачи составим систему уравнений:

х + у = 12,

х – у = 2;

Ответ: искомые числа 7 и 5

13)Видеоролик: задачи решаемые с помощью систем уравнений

14) Составьте систему уравнений по условию задачи:

• На двух полках 60 книг. На второй полке на 10 книг меньше, чем на первой. Сколько книг на каждой полке ?»

• «Автомобиль проехал некоторое расстояние за 30 минут. За какое время проедет это же расстояние велосипедист, скорость которого в 5 раз меньше?»

IV Домашнее задание: Домашняя контрольная работа.

V Итог урока: Рефлексия.

Системы двух уравнений с двумя неизвестными

Цель урока:

• Содействовать обобщению и систематизации знаний учащихся по теме “Решение систем уравнений”; продолжить закрепление следующих умений: решение систем уравнений графическим способом, способом подстановки, способом сложения .
• Развитие познавательного интереса, совершенствовать навыки решения систем уравнений;
• Обобщить знания основного программного материала.

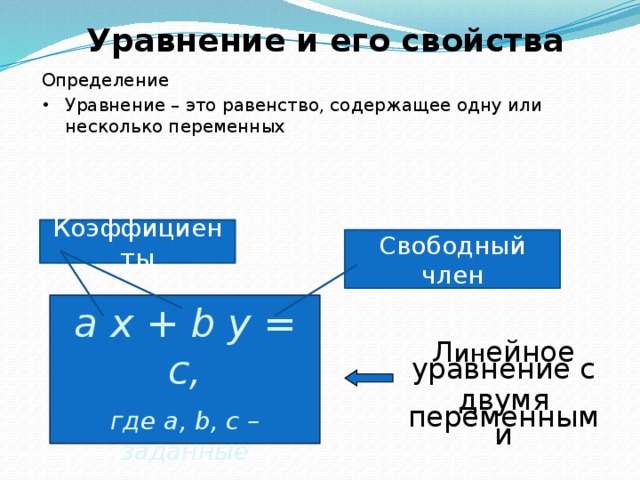
Уравнение и его свойства

Определение

• Уравнение – это равенство, содержащее одну или несколько переменных

Коэффициенты

Свободный член

ax+by=c

а x + b y = c,

где а, b, c – заданные

числа.

Л ин ейное уравнение с

двумя переменными

Из истории уравнений

• Уравнение с двумя неизвестными выражает зависимость между двумя величинами , имеет бесчисленное множество реше -ний и является неопределенным.
• Решением таких уравнений занимались в древности китайцы, греки и индийцы.
• В «Арифметике» Диофанта приведено много задач, решаемых им с помощью неопределенных уравнений.

Диофант из

Александрии

( 3 век )

Решением уравнения с двумя неизвестными х и у

• называется упорядоченная пара чисел ( х ; у ), при подстановке которых в это уравнение получается верное числовое равенство.

- Заданные числа, а х и у - неизвестные

Система уравнений и её решение

Определение

Системой двух линейных уравнений с двумя неизвестными называются два уравнения, объединенные фигурной скобкой.

Фигурная скобка означает, что эти уравнения должны быть решены одновременно.

В общем виде систему двух линейных уравнений с двумя неизвестными записывают так :

а 1 х + b 1 y = c 1,

а 2 х + b 2 y = c 2 ;

а 1 , b 1 , c 1 ,

а 2 , b 2 , c 2

где

Из истории систем уравнений

Задачи на составление и

решение систем уравнений

встречаются в вавилонских

и египетских текстах II

тысячелетия до н. э., в трудах

древнегреческих, китайских

и индийских ученых.

Нижние индексы при буква

впервые употребил в 1675 г.

немецкий математик Лейбниц

Лейбниц

Готфрид Вильгельм

( 1646 – 1716 )

Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство

Решить систему уравнений - это значит найти все её решения или установить, что их нет

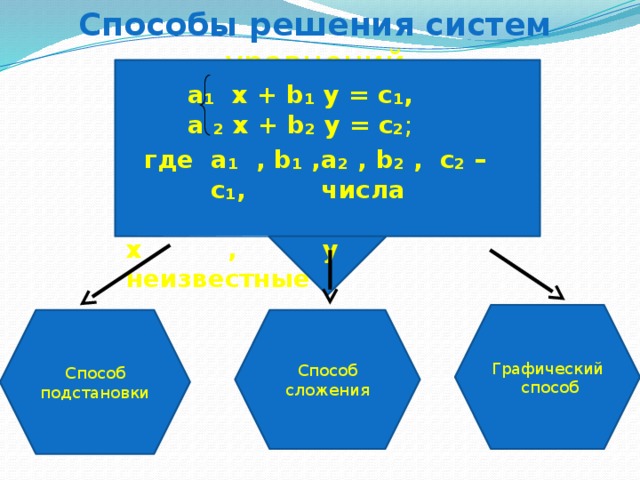
Способы решения систем уравнений

а₁ х + b₁ y = c₁,

а ₂ х + b₂ y = c₂ ;

где а₁ , b₁ , c₁,

а₂ , b₂ , c₂ – числа

х , у неизвестные

Графический способ

Способ

Способ

подстановки

сложения

Способ подстановки

• Самым первым, самым главным Этот способ назову Применяет его каждый  Изучить вам помогу.
• По две буквы в уравненьях Вам их следует найти Но для этого смекалку  Мой дружочек примени.
• Из любого уравненья Букву вырази одну И в другое, без сомненья,  Подстановку совершу.

• Получу я уравненье -  Неизвестное одно, Я найду его решенье,  То - какое-то число.
• И число я в уравненье Вместо буквы запишу Чтоб найти вторую букву Вычисленья завершу.
• Получу ответ: икс, игрек И система решена В круглых скобках пара чисел Запись эта так важна.

Задание. Заполните пропуски.

Система

Система

Наиболее рациональный

Наиболее рациональный

х + 4у = 19,

Выразить…… … .. из …… ……

х + 4у = 19,

способ ее решения – способ

Выразить…… … .. из …… ……

способ ее решения – способ

2х - 3у = 5.

подстановки

уравнения системы и подставить полученное выражение в ( во) ...... ....... уравнение системы

Выразить……….. из …………

3х - 8у = 9,

уравнения системы и подставить полученное выражение в ( во) ...... ....... уравнение системы

3х - 8у = 9,

Выразить……….. из …………

2х - 3у = 5.

подстановки

уравнения системы и подставить полученное выражение в ( во) ............. уравнение системы

уравнения системы и подставить полученное выражение в ( во) ............. уравнение системы

5х + у = 1.

5х + у = 1.

Система

Наиболее рациональный

х + 4у = 19,

Выразить…… … .. из …… ……

способ ее решения – способ

уравнения системы и подставить полученное выражение в ( во) ...... ....... уравнение системы

Выразить……….. из …………

3х - 8у = 9,

2х - 3у = 5.

подстановки

уравнения системы и подставить полученное выражение в ( во) ............. уравнение системы

5х + у = 1.

Графический способ

• Благодаря методу координат, созданному в 17 веке Ферма и Декартом, стало возможным геометрическое решение уравнений систем. Так называемый графический метод решения состоит в построении абсциссы х и ординаты у точки пересечения двух соответствующих прямых.

Решите графически систему уравнений.

Способ сложения

• Запишу два уравненья, Неизвестных тоже два. Применю способ сложенья Им владею я сполна Я домножу уравненья На число непросто так Чтобы выполнить сложенье, Между ними ставим знак. В левой части икс и игрек Аккуратно я сложу Получу одну лишь букву, Её корнем назову. Эту букву я подставлю В уравненье номер два И вторую найду букву, Всё, система решена.
• Нет способа верней.

Составьте систему уравнений по условию задачи:

• «На двух полках 60 книг. На второй полке на 10 книг меньше, чем на первой. Сколько книг на каждой полке ?»
• «Автомобиль проехал некоторое расстояние за 30 минут. За какое время проедет это же расстояние велосипедист, скорость которого в 5 раз меньше?»

Самостоятельная работа

• Домашнее задание Домашняя контрольная работа №3 ( стр 80 по вариантам).

• Рефлексия
• Рефлексия
• Рефлексия

• Какие способы решения вы знаете?
• Какие мы использовали сегодня?
• Какие вам больше нравятся и почему?
• Что вам на уроке понравилось?

• Итог урока
• Оценивание учащихся.

Спасибо всем за работу
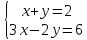
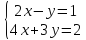
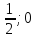