Алгебра
11 класс
Учебник: Мордкович А.Г. Алгебра и начала математического анализа. 10-11 классы. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений (базовый уровень) / [А.Г. Мордкович и др.]; под ред. А.Г. Мордковича. – 10 изд., стер. – Мнемозина, 2009.
Алгебра и начала математического анализа. 10-11 классы. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений (базовый уровень) / А.Г. Мордкович. – 10 изд., стер. – Мнемозина, 2009.
Уровень обучения – базовый
Тема урока: Логарифмическая функция, её свойства и график.
Общее количество часов, отведенное на изучение темы – 3 часа.
Место урока в системе уроков по теме – урок решения ключевых задач
Цель урока – формирование понятия логарифмической функции.
Задачи урока: Образовательные: 1. Закреплять понятие логарифма, логарифмической функции, основные формулы. 2. Учить решать типовые задачи с использованием логарифмической функции. Развивающие: 1. Развивать аналитическое мышление. 2. Развивать зрительную память. 3. Развивать математическую речь учащихся. Воспитательные: 1. Воспитывать ответственное отношение к учебе. 2. Воспитывать графическую культуру.
Планируемые результаты: Знать: определение логарифмической функции, свойства функции в зависимости от основания логарифма. Уметь: строить и читать графики логарифмической функции, находить наибольшее и наименьшее значения функции на заданном промежутке.
Техническое обеспечение урока: мультимедийный проектор, экран
Дополнительное методическое и дидактическое обеспечение урока - сайт mathege.ru, сайт http://interneturok.ru
Содержание урока.
Организационный момент
Здравствуйте, ребята. Давайте вспомним, что мы изучали на прошлом уроке. (Учащиеся называют тему прошлого урока). Достаточно ли хорошо вы изучили этот материал? Можете ли вы использовать изученный материал для решения задач? (Учащиеся: пока ещё нет, нужно научиться применять знания о логарифмической функции для решения задач). Верно. Значит, сегодня нам нужно продолжить изучение темы «Логарифмическая функция, её свойства и график» и научиться решать типовые задачи.
Откройте, пожалуйста, тетради. Запишите дату и тему урока. (Тема урока на экране)
Самостоятельная работа (подготовка к ЕГЭ).
Но, прежде чем начинать решать задачи по теме урока, уделим несколько минут подготовке к ЕГЭ и повторению изученного ранее. На экране две задачи. В вашем распоряжении ровно три минуты на их решение. В тетради нужно записать очень краткое решение и ответ.
а) На рисунке изображен график 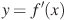 — производной функции f(x), определенной на интервале (-18;6). Найдите количество точек минимума функции f(x), принадлежащих отрезку [-13;1]. (Чертёж к задаче в презентации, Приложение)
— производной функции f(x), определенной на интервале (-18;6). Найдите количество точек минимума функции f(x), принадлежащих отрезку [-13;1]. (Чертёж к задаче в презентации, Приложение)
б) На рисунке изображены график функции у = f(x) и касательная к нему в точке с абсциссой  . Найдите значение производной функции у = f(x) в точке x0. (Чертёж к задаче в презентации, Приложение)
. Найдите значение производной функции у = f(x) в точке x0. (Чертёж к задаче в презентации, Приложение)
Анализ заданий и решений самостоятельной работы. Взаимопроверка.
Время на решение задач закончилось. Обменяйтесь, пожалуйста, тетрадями. Как вы решили задачу под буквой а? (Учащиеся объясняют, дают ответ) Поставьте плюс, если решение верное, минус, если решение неверное, и плюс-минус, если допущена ошибка вычислительного характера. Как вы решили задачу под буквой б?
Теперь возьмите свои тетради и посмотрите результат. Те ребята, у которых имеются минусы, выполните дома работу над ошибками – решите по три аналогичных задачи с сайта mathege.ru (задание №7).
Повторение (фронтальный опрос)
Итак, переходим к изучению логарифмической функции. Очень быстро вспомним определение логарифмической функции (учащиеся отвечают). Перечислите, пожалуйста, свойства логарифмической функции.
Молодцы. Ответьте, пожалуйста, на следующие вопросы.
А1. График какой функции изображен на рисунке? (чертежи выводятся на экран) Почему вы так решили?
| 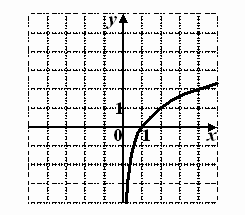
| 1) | у = 2х |
| 2) | у = log2х |
| 3) | у = (0,5)х |
| 4) | у = log0,5х |
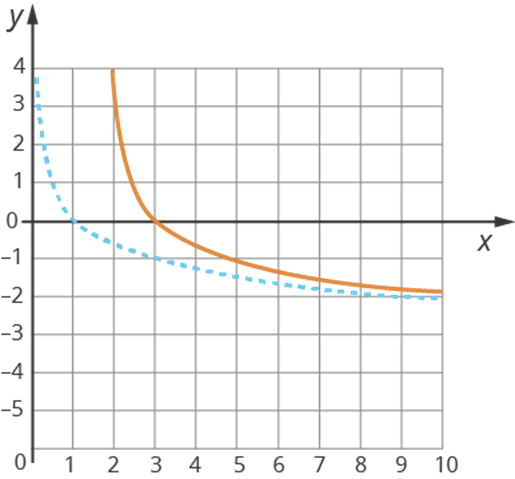
А2. График какой функции изображен на рисунке? Обоснуйте ответ
| 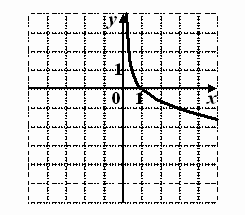
| 1) | у = 3х |
| 2) | у = log3х |
| 3) | 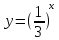
|
| 4) | 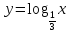 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
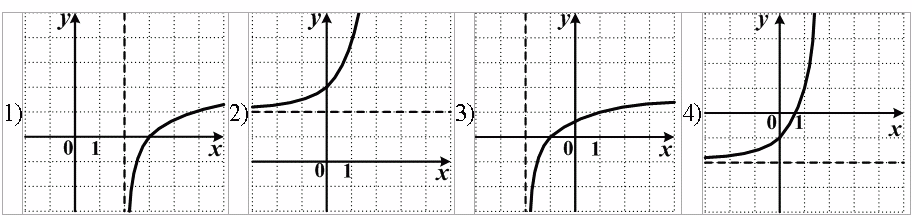
А3. На одном из рисунков изображен эскиз графика функции 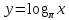 . Укажите номер этого рисунка.
. Укажите номер этого рисунка.
А4. На одном из рисунков изображен эскиз графика функции 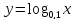 . Укажите номер этого рисунка.
. Укажите номер этого рисунка.
А5. На одном из рисунков изображен эскиз графика функции 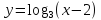 . Укажите номер этого рисунка. Тогда каким функциям принадлежат остальные графики?
. Укажите номер этого рисунка. Тогда каким функциям принадлежат остальные графики?
Решение типовых задач
I) Решение простейших уравнений и неравенств.
Ребята, как вы считаете, какую самую первую, самую главную типовую задачу нужно научиться решать? (Научиться решать уравнения). Верно, сначала мы научимся использовать график логарифмической функции для решения простейших уравнений и неравенств. Как это делать, подробно и понятно и написано в учебнике.
Работа с учебником – стр. 254 (учащиеся самостоятельно читают, затем один из учащихся воспроизводит решение на доске)

(Решение примера смотри в презентации, Приложение)
Решим аналогичную задачу.

II) Ребята, ещё одной важной типовой задачей является оценка логарифмических констант. (разбор решения совместно с учителем)
Пример 1 – оценить числа:
а) log27 б) log23
Рассмотрим логарифмическую функцию с основанием 2:
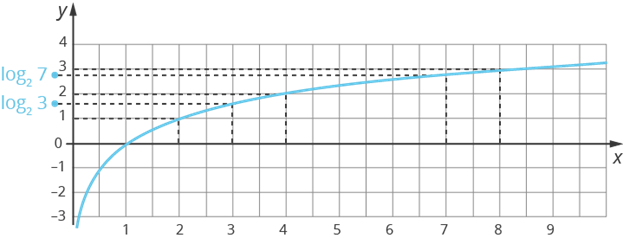
При х=1 функция равна нулю. Покажем некоторые степени двойки. Например, х = 2 (первая степень), при этом у = 1; х = 4 (вторая степень), при этом у = 2; х = 8 (третья степень), при этом у = 3
Аргумент х = 7 расположен между х = 4 и х = 8 , отсюда значение функции у(7) = log27 расположено между двойкой и тройкой.
Аналогично аргумент х = 3 расположен между х = 2 и х = 4 , отсюда значение функции у(3) = log23 расположено между единицей и двойкой.
Ответ: а) 2 log27 log23
Пример 2 – решить неравенство: (log530 – log210)x 0
Очевидно, что решение сводится к оценке логарифмических констант.
Итак, оценим первый логарифм, второй логарифм, а затем всю скобку.
2 log530 2 3
3 log210 3 4
Таким образом, первый логарифм лежит в пределах от двух до трех, а второй – от трех до четырех, очевидно, что их разность меньше либо равна нулю. Таким образом, чтобы выполнялось заданное неравенство необходимо чтобы х был отрицательным.
Ответ: (-∞;0)
Давайте проверим себя, как мы научились оценивать логарифмические константы.
Работа с задачником - самостоятельное решение по вариантам (один вариант решает под буквой а, другой – под буквой б) и проверка решения на доске (от каждого варианта выходят по одному человеку и выписывают решение)

А как вы решите следующие задачи? Каким свойством логарифмической функции вы воспользуетесь? Верно, воспользуемся свойством монотонности логарифмической функции. (самостоятельное решение задач и устная проверка решений с комментированием)


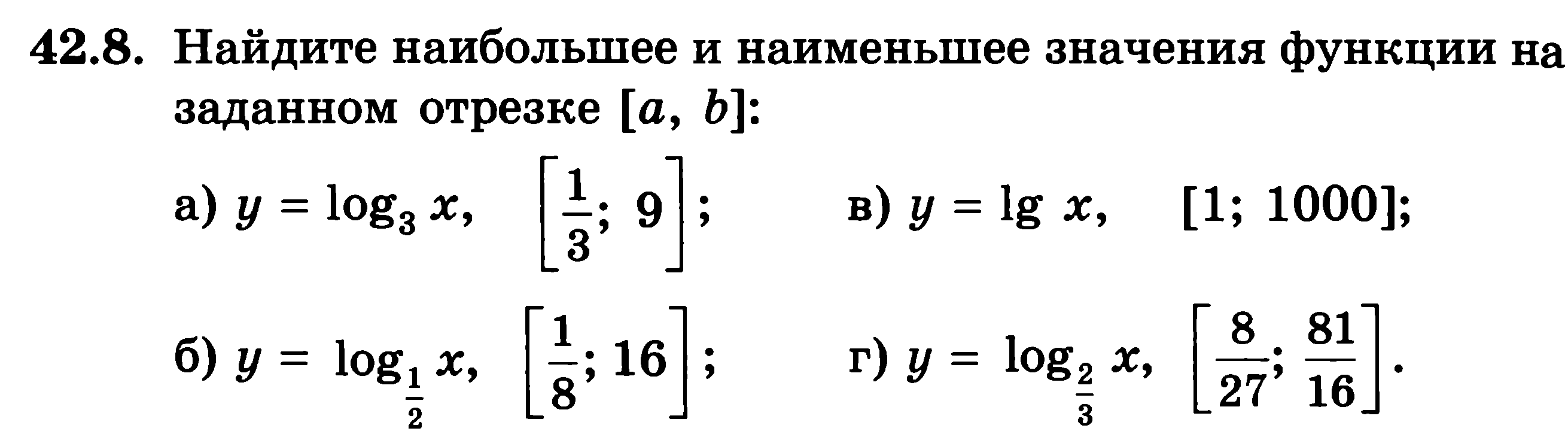

III) Следующая типовая задача – построение графиков логарифмических функций (фронтальная работа)
Пример 1 – построить график функции: 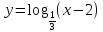
Как вы будете строить график этой функции? Какое преобразование графика здесь применяется?
Чтобы уверенно решать подобные задачи, нужно знать внешний вид графика логарифмической функции и знать правила преобразования графиков. В данном случае первым действием мы строим график функции 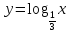 , а вторым сдвигаем его на две единицы вправо.
, а вторым сдвигаем его на две единицы вправо.
В следующих задачах важно учитывать область определения.
Пример 2 – построить график функции:
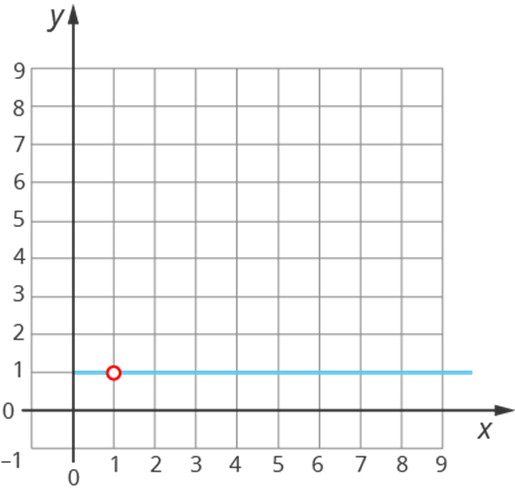
а) y = logxx
Как бы вы построили график этой функции? С чего мы начинаем исследование функции? Верно, с нахождения области определения. Найдем область определения. Заданный логарифм существует, когда аргумент больше нуля и не равен единице: x 0, x ≠ 1,
Но тогда y = 1, т.к. x1 = x
Получаем график функции:
б) 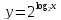
И снова – с чего начинается построение графика функции? Какая область определения у этой функции? Заданная функция определена, когда аргумент строго больше нуля: x 0.
Но тогда, согласно основному логарифмическому тождеству, y = x. Получаем график функции:
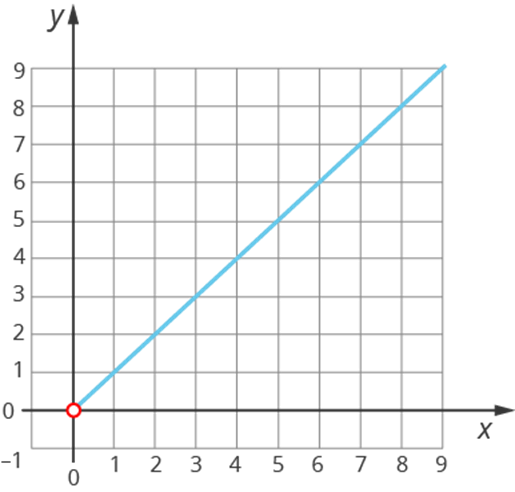
IV) Переходим к решению следующей типовой задачи – нахождению области значений функции
Пример – найти область значений функции: 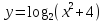
Рассмотрим вспомогательную функцию 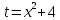
Это квадратичная функция, x2 ≥ 0 значит, t ≥ 4
Теперь задача сводится к нахождению области значений следующей функции:
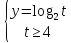
Данная функция нам знакома, мы знаем, что логарифмическая функция с основанием 2 монотонно возрастает, исходя из этого, нам достаточно найти значение функции при t = 4 :
y (4) = log2 4 = 2
Ответ: [2; + ∞)
Давайте проверим, как вы научились решать этот тип задач.
Закрепление - работа с учебником (самостоятельно, с взаимопроверкой):
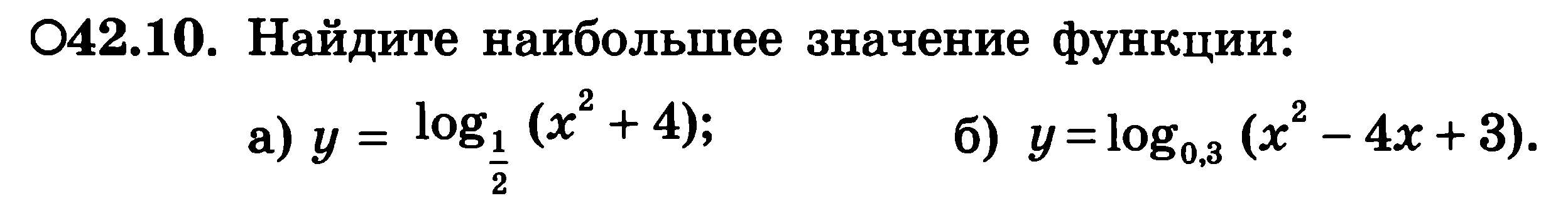
Домашнее задание: №№ 42.6, 42.8 вг, 42.10 вг
Подведение итогов урока
Итак, давайте вспомним – какие типовые задачи мы сегодня рассмотрели (учащиеся отвечают). Все ли задачи вы научились решать? Легко ли вам будет их решить самостоятельно, если это понадобится? Как вы оцениваете свою работу на этом уроке?