Презентации содержат теоретический материал, изложенный в доступной для обучающихся форме, а также пошаговое решение уравнений и неравенств, содержищих неизвестное под знаком модуля. Материал может быть использован при проведении уроков повторения и обобщения знаний по теме, а также для самостоятельной работы обучающихся, пропустивших занятия в школе.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Презентации к урокам алгебры по теме "Модуль числа. Уравнения и неравенства, содержащие модуль"
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого презентации
«У - 1_Модуль числа. Уравнения, содержащие модуль»
Просмотр содержимого презентации
«У - 2_Модуль числа. Неравенства, содержащие модуль»
Полезное для учителя
Распродажа видеоуроков!
2200 руб.
3140 руб.
2000 руб.
2860 руб.
2050 руб.
2930 руб.
830 руб.
1190 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства


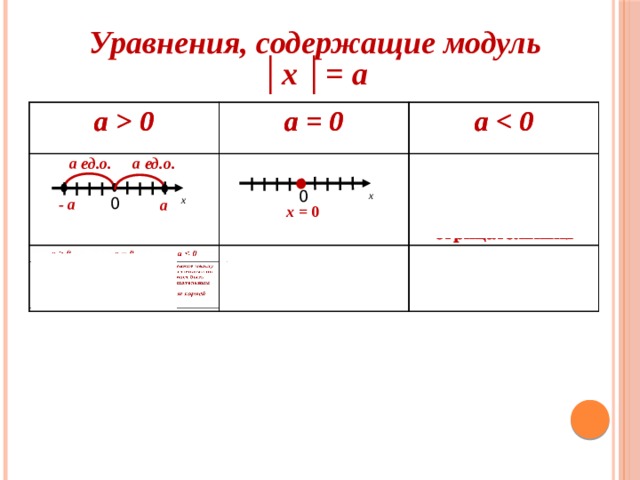 0 a 0 a = 0 a = 0 2 корня: = – a , a a 1 корень: х = 0 1 корень: х = 0 = a расстояние между двумя точками не может быть отрицательным расстояние между двумя точками не может быть отрицательным Нет корней Нет корней а ед.о. а ед.о. 0 х 0 х - a a х = 0" width="640"
0 a 0 a = 0 a = 0 2 корня: = – a , a a 1 корень: х = 0 1 корень: х = 0 = a расстояние между двумя точками не может быть отрицательным расстояние между двумя точками не может быть отрицательным Нет корней Нет корней а ед.о. а ед.о. 0 х 0 х - a a х = 0" width="640"

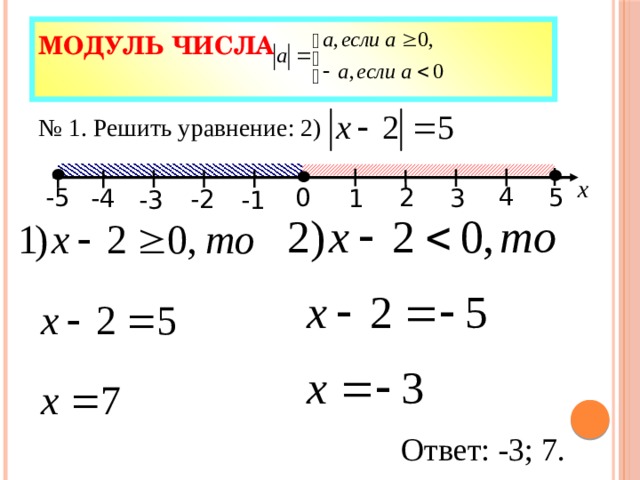




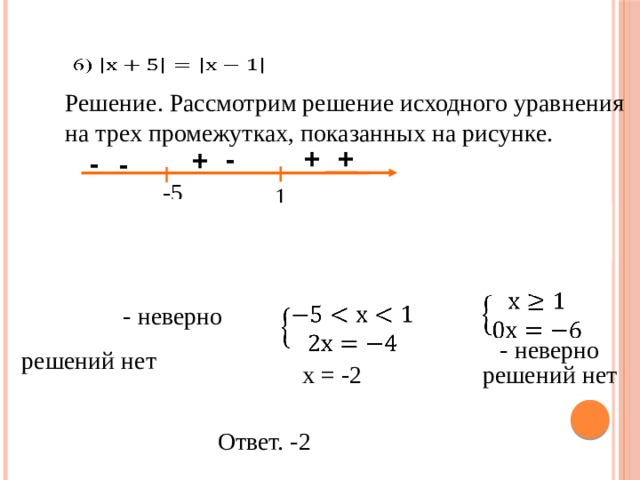
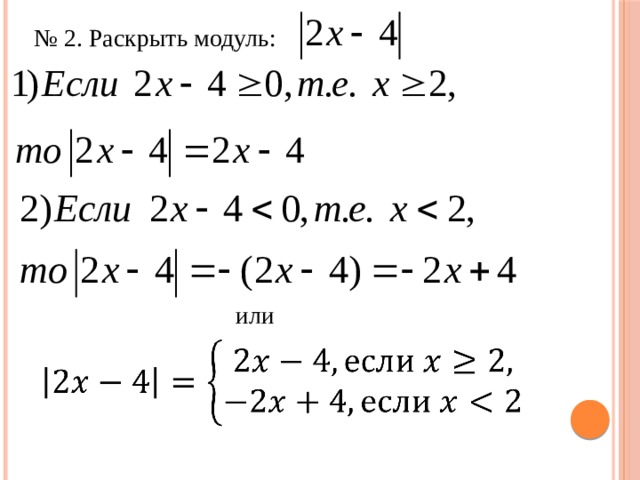
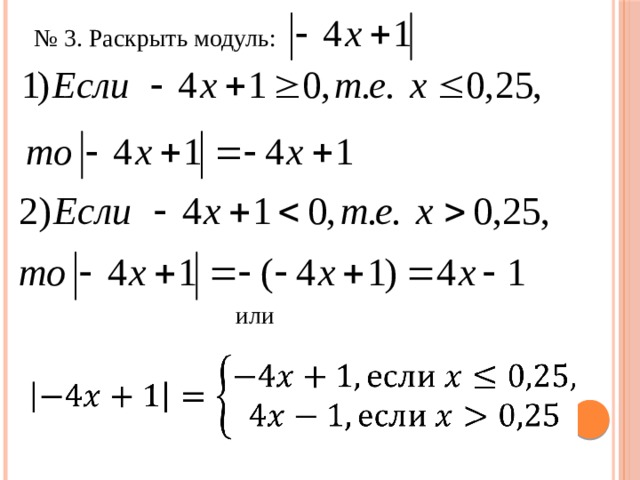
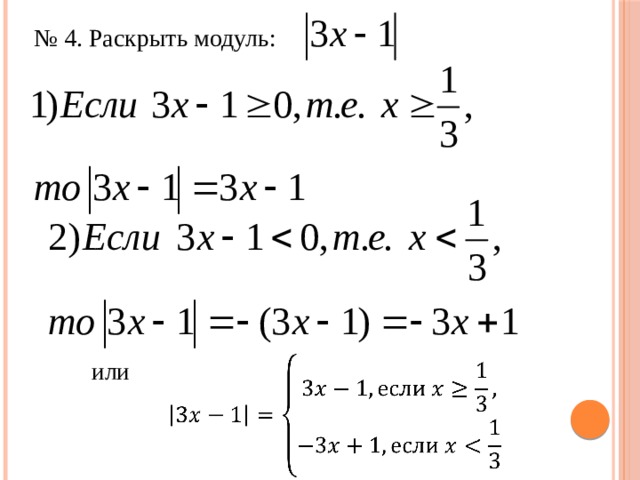




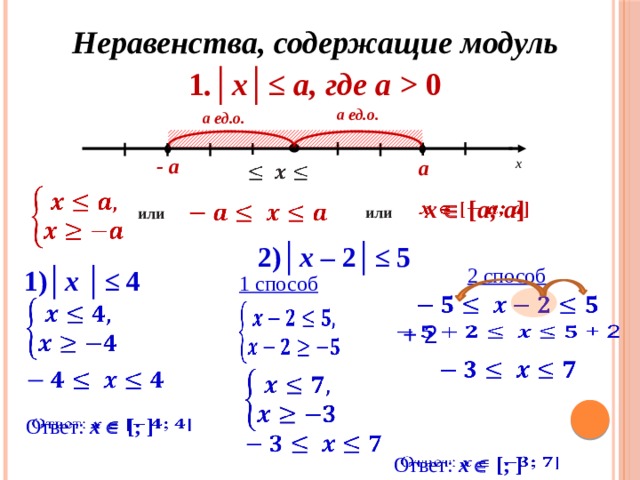 0 а ед.о. а ед.о. - a a х 0 х [ а; а ] или или 2) │х – 2 │≤ 5 2 способ 1) │х │≤ 4 1 способ + 2 Ответ: х [; ] Ответ: х [; ] " width="640"
0 а ед.о. а ед.о. - a a х 0 х [ а; а ] или или 2) │х – 2 │≤ 5 2 способ 1) │х │≤ 4 1 способ + 2 Ответ: х [; ] Ответ: х [; ] " width="640"
 0 8 ≤ 3 х ≤ 12 : 3 0 : 3 0 ≤ х ≤ 4 ≤ х ≤ 4 Ответ: х [; ]" width="640"
0 8 ≤ 3 х ≤ 12 : 3 0 : 3 0 ≤ х ≤ 4 ≤ х ≤ 4 Ответ: х [; ]" width="640"


 0 а ед.о. а ед.о. - a a х 0 х ( а; а ) или или 1) │ 12 х│ 5 2) │ 5 4 х│ 11 11 5 4 х 11 11 5 4 х 11 5 : (– 4) 16 4 х 6 х 4 х , Ответ: х (7; Ответ: х (1,5; " width="640"
0 а ед.о. а ед.о. - a a х 0 х ( а; а ) или или 1) │ 12 х│ 5 2) │ 5 4 х│ 11 11 5 4 х 11 11 5 4 х 11 5 : (– 4) 16 4 х 6 х 4 х , Ответ: х (7; Ответ: х (1,5; " width="640"
 0 0 ед.о. х 0 " width="640"
0 0 ед.о. х 0 " width="640"
 0 а ед.о. а ед.о. - a a х 0 или или или х ( − ∞ ; − а ] [ а ; + ∞) 2) │ 3 х – 5 │≥ 4 1) │х │≥ 2 или 3 х – 5 ≥ 4 3 х – 5 ≤ – 4 3 х ≥ 4 + 5 3 х ≤ – 4 + 5, 3 х ≥ 9 3 х ≤ 1, х ≥ 3 х ≤ Ответ: х ( − ∞ ; − 2] [2; + ∞) Ответ: х ( − ∞ ; ] [3; + ∞) " width="640"
0 а ед.о. а ед.о. - a a х 0 или или или х ( − ∞ ; − а ] [ а ; + ∞) 2) │ 3 х – 5 │≥ 4 1) │х │≥ 2 или 3 х – 5 ≥ 4 3 х – 5 ≤ – 4 3 х ≥ 4 + 5 3 х ≤ – 4 + 5, 3 х ≥ 9 3 х ≤ 1, х ≥ 3 х ≤ Ответ: х ( − ∞ ; − 2] [2; + ∞) Ответ: х ( − ∞ ; ] [3; + ∞) " width="640"
 а, где а 0 а ед.о. а ед.о. - a a х 0 или или или х ( − ∞ ; − а ) ( а ; + ∞) │ 2 – 0 , 5 х│ 2 или 2 – 0,5 х 2 2 – 0 , 5 х 2 2 – 2 0,5 х 2 + 2 0 , 5 х , 0 0,5 х 4 0,5 х ∙ 10 0 0 х : 5 0 40 5 х х 0 Ответ: х ( − ∞ ; (8; + ∞) х 8 8" width="640"
а, где а 0 а ед.о. а ед.о. - a a х 0 или или или х ( − ∞ ; − а ) ( а ; + ∞) │ 2 – 0 , 5 х│ 2 или 2 – 0,5 х 2 2 – 0 , 5 х 2 2 – 2 0,5 х 2 + 2 0 , 5 х , 0 0,5 х 4 0,5 х ∙ 10 0 0 х : 5 0 40 5 х х 0 Ответ: х ( − ∞ ; (8; + ∞) х 8 8" width="640"
 0 х 0 или или или х ( − ∞; 0) (0; + ∞) х 0 │ 7 – 2 х│ 0 или 1 способ 2 способ или 7 – 2 х 0 7 – 2 х 0 7 – 2 х 0 7 2 х : 2 0 7 2 х : 2 0 : 2 7 2 х 3,5 х 3,5 3,5 х х 3,5 х 3,5 Ответ: х Ответ: х ( − ∞ ; (3,5; + ∞)" width="640"
0 х 0 или или или х ( − ∞; 0) (0; + ∞) х 0 │ 7 – 2 х│ 0 или 1 способ 2 способ или 7 – 2 х 0 7 – 2 х 0 7 – 2 х 0 7 2 х : 2 0 7 2 х : 2 0 : 2 7 2 х 3,5 х 3,5 3,5 х х 3,5 х 3,5 Ответ: х Ответ: х ( − ∞ ; (3,5; + ∞)" width="640"