МУНИЦИПАЛЬНОЕ КАЗЕННОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ КРУТОЯРСКАЯ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА
УРОК - ОСНОВНАЯ ФОРМА ОРГАНИЗАЦИИ ОБУЧЕНИЯ В ШКОЛЕ
Выполнила: Каптилова В.А., учитель математики 1 квалификационной категории
АНОТАЦИЯ
В данной работе рассмотрены различные типы уроков и рассмотрено строение основных видов уроков. Так же в работе предложены разработки некоторых типов уроков.
Оглавление
Введение______________________________________________________ 4
1. Урок – основная форма организации обучения в школе____________5-6
2. Типология уроков ___________________________________________7-8
3. Строение уроков основных типов_____________________________9-34
4. Разработки уроков некоторых типов (из опыта работы)__________35-71
5. Литература ________________________________________________72
Введение
Вопросы активизации познавательной деятельности учащихся относятся к числу наиболее актуальных проблем современной педагогической науки и практики. Реализация принципа активности в обучении имеет большое значение, т.к. обучение и развитие носят деятельностный характер, и от качества учения как деятельности зависит результат обучения, развития и воспитания учащихся.
Формирование интереса к учению – важное средство повышения качества обучения. Это особенно важно в школе, когда еще формируются и определяются интересы к тому или иному предмету. Чтобы формировать у учащихся умение самостоятельно пополнять свои знания, необходимо воспитывать у детей интерес к учению, потребность в знаниях.
Одно из важнейших факторов развития к учению – понимание детьми того или иного изучаемого материала. Для развития познавательного интереса к изучаемому материалу большое значение имеет методика преподавания данного материала.
Поэтому, перед тем как приступить к изучению какой-либо темы учитель должен большое внимание уделить поиску активных форм и методов обучения, продумывая каждый урок и его тип..
Актуальность данной темы состоит в том, что важным звеном в системе обучения и воспитания является урок. Различные типы уроков позволяют использовать все уровни усвоения знаний: от воспроизводящей деятельности через преобразующую к главной цели - творческо-поисковой деятельности. Творческо-поисковая деятельность оказывается более эффективной, если ей предшествует воспроизводящая и преобразующая деятельность, в ходе которой учащиеся усваивают приемы учения.
Целью данной работы является анализ различных типов уроков, а также их практическое применение.
1. УРОК - ОСНОВНАЯ ФОРМА ОРГАНИЗАЦИИ ОБУЧЕНИЯ В ШКОЛЕ
"Урок — это солнце, вокруг которого, как планеты,
вращаются все другие формы учебных занятий".
Н.М. Верзилин
Что же такое урок?
До настоящего времени в педагогической науке преобладающим является мнение, согласно которому урок — это систематически применяемая для решения задач обучения, воспитания и развития учащихся, форма организации деятельности постоянного состава учителей и учащихся в определенный отрезок времени.
Урок — это форма организации обучения с группой учащихся одного возраста, постоянного состава, занятие по твердому расписанию и с единой для всех программой обучения. В этой форме представлены все компоненты учебно-воспитательного процесса: цель, содержание, средства, методы, деятельность по организации и управлению и все его дидактические элементы. Сущность и назначение урока в процессе обучения как целостной динамической системы сводится, таким образом, к коллективно-индивидуальному взаимодействию учителя и учащихся, в результате которого происходит усвоение учащимися знаний, умений и навыков, развитие их способностей, опыта деятельности, общения и отношений, а также совершенствование педагогического мастерства учителя. Тем самым урок, с одной стороны, выступает как форма движения обучения в целом, с другой, — как форма организации обучения, предопределяемая основными требованиями к организационному построению урока учителем, вытекающими из закономерностей и принципов обучения. Руководствуясь ими, учитель подготавливает урок как систему подлежащих решению дидактических задач (образования, воспитания и развития) в процессе обучения данным конкретным составом учащихся в конкретных условиях жизнедеятельности школы.
Согласно концепции М.И. Махмутова, можно сформулировать следующим образом: «Урок — это динамичная и вариативная форма организации процесса целенаправленного взаимодействия (деятельностей и общения) определенного состава учителей и учащихся, включающая содержание, формы, методы и средства обучения и систематически применяемая (в одинаковые отрезки времени) для решения задач образования, развития и воспитания в процессе обучения».
Функция урока как организационной формы обучения состоит в достижении завершенной, но частичной цели, которая, например, в одном случае состоит в усвоении нового, целостного содержания, пусть являющегося частью более обширного содержания, в другом — в частичном усвоении на уровне осознанного восприятия и запоминания (закрепления). В первом случае структура урока как целостной системы будет повторять в основном структуру обучения как целостного процесса, во втором — лишь частично отразит целостный процесс обучения. Это говорит о том, что особенности урока как организационной формы обучения обусловлены целью и местом каждого отдельно взятого урока в целостной системе учебного процесса
Таким образом, урок многогранен и многопланов. В нем, как уже отмечалось выше, как в целостном отрезке процесса обучения взаимодействуют все компоненты этого сложного процесса — его общие педагогические цели, дидактические задачи, содержание, методы, материальное оснащение и др.
Решая конкретные задачи в каждом отдельно взятом временном отрезке учебного процесса, урок является частью темы, курса учебного предмета и соответственно занимает свое место в системе учебного предмета, темы программы, решает обозначенный в нем на данный момент дидактические цели, соотнесенные с учебно-воспитательными задачами курса. «Но для этого урок сам должен иметь свою строгую, единую внутреннюю логику, определенную дидактическими целями, средствами, методами и приемами обучения.
Рождение любого урока начинается с осознания и правильного, четкого определения его конечной цели — чего учитель хочет добиться; затем установления средства — что поможет учителю в достижении цели, а уж затем определения способа — как учитель будет действовать, чтобы цель была достигнута.
Что же такое цель урока?
В науке общепринято, что цель - это предполагаемый, заранее планируемый (мысленно или вербально) результат деятельности по преобразованию какого-либо объекта. В педагогической деятельности объектом преобразования является деятельность обучающегося, а результатом — уровень обученности, развитости и воспитанности учащегося. Поэтому цели урока ставятся в соответствии с целями обучения и образования, как системы более высокого порядка и не могут сводиться, как это было в период, когда деятельность преподавания рассматривалась только как передача учащимся готовых выводов науки и «целям организации» занятий — «изучить такой-то объем нового материала», «повторить такие-то разделы программы» и т.п. Такая постановка цели урока в современной школе несостоятельна.
Цель урока в современной школе должна отличаться конкретностью, с указанием средств ее достижения и ее переводом в конкретные дидактические задачи.
Так, для того чтобы достичь цели урока, например, по математике, необходимо продуманно решить три основные дидактические задачи:
актуализировать прежние знания, умения и навыки, непосредственно связанные с темой урока;
сформировать у учащихся новые понятия и способы действия;
организовать применение учащимися знаний и опыта деятельности с целью формирования у них новых учебных и познавательных умений и навыков, нового опыта познавательной деятельности.
Дидактические задачи урока реализуются в реальной педагогической действительности через учебные задачи (задачи для учащихся). Это решение учащимися арифметических задач, выполнение всевозможных упражнений, разбор предложений, составление плана пересказа и т.п. Эти задачи отражают учебную деятельность учащихся в конкретных учебных ситуациях. Дидактические и учебные задачи в целостной структуре урока выступают, таким образом, основным средством достижения цели и условием отбора, конструирования способа действия, как учителя, так и учащихся.
Развитие познавательных творческих способностей учащихся – одна из целей деятельности учителя на уроке, а применение различных типов уроков и разных приемов активизации знаний учащихся на этих уроках является средством достижения цели. Понимание этого важно для работы учителя. Заботясь о развитии учащихся, необходимо чаще использовать разные виды уроков в учебной деятельности. Но одновременно необходимо отдавать себе отчет в том, являются ли используемые приемы и методы оптимальными, отвечающими имеющемуся развитию учащихся и задаче дальнейшего совершенствования их познавательных умений.
Применяя некоторые из типов уроков необходимо всегда учитывать имеющийся уровень развития познавательных способностей учащихся.
Как уже говорилось ранее, урок является сложным педагогическим объектом. Как и всякие сложные объекты, уроки могут быть разделены на типы по различным признакам. Этим объясняется существование многочисленных классификаций уроков.
Рассмотрим типологии уроков, которые в теории и практике обучения занимают ведущее место.
2. Типология уроков
В теории и практике обучения ведущее значение отводится следующим типологиям уроков:
По основной дидактической цели выделяют такие типы уроков:
урок ознакомления с новым материалом;
урок закрепления изученного;
урок применения знаний и умений;
урок обобщения и систематизации знаний;
урок проверки и коррекции знаний и умений;
комбинированный урок.
Типологией по основному способу проведения их подразделяют на уроки:
в форме беседы;
лекции;
экскурсии;
киноуроки;
самостоятельная работа учащихся;
лабораторные и практические работы;
сочетание различных форм занятий.
По основным этапам учебного процесса выделяют уроки:
вводные;
первичного ознакомления с материалом;
образования понятий, установления законов и правил;
применение полученных правил на практике;
повторения и обобщения4
контрольные;
смешанные и комбинированные.
Уроки, которые конструируются в практике обучения разделяют не только по типам, но и по видам.
Деление уроков на виды осуществляется по характеру деятельности учителя и учащихся. При этом подразделение на виды происходит для каждого типа урока в рамках используемой типологии.
Например: КОНТРОЛЬНЫЕ УРОКИ, являющиеся одним из элементов типологии по основным этапам учебного процесса подразделяются на следующие виды:
Подразделение уроков на типы и виды, тем, не менее, не делает
полными имеющиеся типологии.
В качестве примеров подобных типологий, подразделяющих уроки по форме их проведения, можно привести следующие типы уроков:
1. Уроки в форме соревнований и игр:
- конкурс;
- турнир;
- эстафета;
- дуэль;
- КВН;
- деловая игра;
- ролевая игра;
- кроссворд;
- викторина и т.д.
2. Уроки, основанные на формах, жанрах и методах работы, известных в общественной практике:
- исследование;
- изобретательство;
- анализ первоисточников;
- комментарий;
- мозговая атака;
- интервью;
- репортаж;
- рецензия и т.д.
3. Уроки, основанные на нетрадиционной организации учебного материала:
- урок мудрости, откровения;
- урок-блок;
- урок – «дублер начинает действовать» и т.д.
4. Уроки, напоминающие публичные формы общения:
- пресс-конференции;
- аукцион;
- бенефис;
- регламентированная дискуссия;
- телемост;
- репортаж;
- диалог;
- устный журнал и т.д.
5.Уроки, основанные на имитации деятельности учреждений и организаций:
- следствие;
- патентное бюро;
- ученый совет и т.д.
6. Уроки, основанные на имитации деятельности при проведении общественно-культурных мероприятий:
- заочная экскурсия;
- экскурсия в прошлое;
- путешествие;
- прогулки и т.д.
7. Уроки, опирающиеся на фантазию:
- урок-сказка;
- урок-сюрприз и т.д.
8. Использование на уроке традиционных форм внеклассной работы:
- «следствие ведут знатоки»;
- «брейн-ринг»;
- диспут;
9. Интегрированные уроки.
10. Трансформация традиционных способов организации урока:
- лекция-парадокс;
- парный опрос;
- экспресс-опрос;
- урок-защита оценки;
- урок-консультация;
- урок практикум;
- урок-семинар и т.д.
В качестве примеров другого подхода к типологии уроков по форме их проведения можно привести такие блоки однотипных уроков:
- урок изобретательства;
- урок-выставка;
- урок-сочинение;
- урок – творческий отчет; и т.д
- урок – общественный смотр знаний;
- урок-диспут;
- урок-диалог и т.д.
- одновременно по двум предметам;
- одновременно для учащихся разных возрастов и т.д.
- урок об ученных;
- урок-бенефис;
- урок – исторический обзор;
- урок-портрет и т.д.
- урок-спектакль;
- урок – воспоминаний;
- урок-суд;
- урок-аукцион и т.д.
- урок – деловая игра;
- урок – ролевая игра;
- урок с дидактической игрой;
- урок-соревнование;
- урок-путешествие и т.д.
- урок-тест;
-урок для родителей;
- урок-консультация.
Сопоставление различных типологий уроков позволяет отметить определенную тенденцию – стремление более полно охватить современные формы организации урока.
В практике обучения конструирование учителем систем уроков, как правило, не укладывается в рамках какой-то одной типологии. При этом приходится решать и проблемы, связанные с выбором или компоновкой той или иной системы уроков. Существенную помощь здесь может оказать знание специфики строения совокупности уроков.
3. Строение уроков основных типов
Реализация идеи использования совокупности уроков, включающих характерные структурные элементы остальных уроков, позволила выявить и подтвердить целесообразность девятнадцати типов уроков:
1) урок ознакомления с новым материалом;
2) урок закрепления изученного;
3) урок применения знаний и умений;
4) урок обобщения и систематизации знаний и умений;
5) урок проверки и коррекции знаний и умений;
6) комбинированный урок;
7) урок-лекция;
8) урок-семинар;
9) урок-зачет;
10) урок практикум;
11) урок-экскурсия;
12) урок-дискуссия;
13) урок-консультация;
14) интегрированный урок;
15) театрализованный урок;
16) урок-соревнование;
17) урок с дидактической игрой;
18) урок - деловая игра;
19) урок – ролевая игра.
При выборе типа урока учитель ориентируется на его строение.
1. Урок ознакомления с новым материалом.
Структура этого урока определяется его основной дидактической целью: введением понятия, установлением свойств изучаемых объектов, построением правил, алгоритмов и т.д.
Основные этапы:
|
1. Сообщение темы, цели, задач урока и мотивация учебной деятельности; 2. Подготовка к изучению нового материала через повторение и актуализацию опорных знаний; 3. Ознакомление с новым материалом; 4. первичное осмысление и закрепление связей и отношений в объектах изучения; 5. Постановка задания на дом; 6. подведение итогов урока.
|
2. Урок закрепления изученного.
Основная дидактическая цель его – формирование определенных умений.
Основные этапы:
|
1. Проверка домашнего задания, уточнение направлений актуализации материала; 2. Сообщение темы, цели и задач урока, мотивация учения; 3. Воспроизведение изученного и его применение в стандартных условиях; 4. Перенос приобретенных знаний и их первичное применение в новых или измененных условиях с целью формирования умений; 5. Подведение итогов урока; 6. Постановка домашнего задания.
|
3. Урок применения знаний и умений.
В процессе применения знаний и умений различают следующие основные звенья:
- воспроизведение и коррекция необходимых знаний и умений;
- анализ заданий и способов их выполнения;
- подготовка требуемого оборудования;
- самостоятельное выполнение заданий;
- рационализация способов выполнения заданий;
- внешний контроль и самоконтроль в процессе выполнения заданий.
Основные этапы:
|
1. Проверка домашнего задания; 2. Мотивация учебной деятельности через осознание учащимися практической значимости применяемых знаний и умений, сообщение темы, цели и задач урока; 3. Осмысление содержания и последовательности применения практических действий при выполнении предстоящих заданий; 4. Самостоятельное выполнение учащимися заданий под контролем учителя; 5. Обобщение и систематизация результатов выполненных заданий. 6. подведение итогов урока и постановка домашнего задания.
|
4. Урок обобщения и систематизации знаний
На уроках обобщения и систематизации знаний выделяют наиболее общие и существенные понятия, законы, закономерности, основные теории и ведущие идеи, устанавливают причинно-следственные и другие связи и отношения между важнейшими явлениями, процессами, событиями, усваивают широкие категории понятий и их систем и наиболее обширные закономерности.
Процесс обобщения и систематизации знаний предполагают такую последовательность действий: От восприятия, осмысления и обобщения отдельных фактов к формированию понятий, их категорий и систем, от них – к усвоению более сложной системы знаний: овладение основными теориями и ведущими идеями изучаемого предмета.
Основные этапы:
|
1. Постановка цели урока и мотивация учебной деятельности учащихся; 2. Воспроизведение и коррекция опорных знаний; 3. Повторение и анализ основных фактов, событий, явлений; 4. обобщение и систематизация понятий, усвоение системы знаний и их применение для объяснения новых фактов и выполнения практических заданий; 5. Усвоение ведущих идей и основных теорий на основе широкой систематизации знаний; 6. Подведение итогов урока.
|
5. Урок проверки и коррекции знаний.
Контроль и коррекция знаний и умений осуществляется на каждом уроке. Но после изучения одной или нескольких подтем или учитель проводит специальные уроки контроля и коррекции, чтобы выявить уровень овладения учащимися комплексом знаний и умений, и на его основе принять определенные решения по совершенствованию учебного процесса.
При определении структуры урока контроля и коррекции, целесообразно исходить из принципа постепенного нарастания уровня знаний и умений, т.е. от уровня осознания до репродуктивного и продуктивного (конструктивного) уровней.
Основные этапы:
|
1. Ознакомление с целью и задачами урока, инструктаж учащихся по организации работы на уроке; 2. Проверка знаний учащимися фактического материала и их умений раскрывать элементарные внешние связи в предметах и явлениях; 3. Проверка знаний учащимися основных понятий, правил, законов и умений объяснять их сущность, аргументировать свои суждения и прводить примеры; 4. Проверка умений учащимися самостоятельно применять знания в стандартных условиях; 5.Проверка умений учащихся применять знания в измененных, нестандартных условиях; 6. Подведение итогов (на данном и последующих уроках). |
6. Комбинированный урок
Комбинированный урок характеризуется постановкой и достижением нескольких дидактических целей. Их многочисленными комбинациями определяются разновидности комбинированных уроков. Традиционной является следующая структура.
Основные этапы:
|
1. Ознакомление с темой урока, постановка его целей и задач; 2. Проверка домашнего задания; 3. Проверка знаний и умений учащихся по пройденному материалу; 4. Изложение нового материала; 5. Первичное закрепление изученного материала; 6. Подведение итогов урока и постановка домашнего задания.
|
Наряду с традиционной в практике обучения широко используются и другие виды комбинированных уроков. Например, комбинированный урок, целью которого является проверка ранее изученного и ознакомление с новым материалом.
Основные этапы:
|
1. Проверка выполнения домашнего задания; 2. проверка ранее усвоенных знаний; 3. Сообщение темы, цели и задач урока; 4. Изложение нового материала; 5. Восприятие и осознание учащимися нового материала; 6. Осмысление, обобщение и систематизация знаний; 7. Постановка домашнего задания.
|
Структура комбинированного урока во многом дублируется и при конструировании так называемых модульных уроков. Они характеризуются постановкой и достижением нескольких дидактических целей, но так, чтобы урок отличался завершенностью и самостоятельностью. Это выражается в том, что структура модульного урока, как правило включает:
- Мотивационную беседу (то, что именуется организационном моментом или введение в новую тему урока), завершающуюся постановкой интегрирующей цели урока;
- Входный контроль (проверка домашнего задания и повторение изученного ранее);
- работу с новым материалом;
- завершающий контроль (проверка усвоенного на уроке)
- рефлекию.
Последнее связано с самооценками и суждениями учащихся о работе класса, группы, своей деятельности на уроке: о том, какое сложилось у каждого ученика мнение об уроке и что им хотелось бы пожелать.
7. Урок-лекция
Это уроки, на которых излагается значительная часть теоретического материала изучаемой темы.
В зависимости от дидактических задач и логики учебного материала распространены следующие лекции:
- вводные;
- установочные;
- текущие;
- обзорные.
По характеру изложения и деятельности учащихся лекция может быть:
- информационная;
- объяснительная;
- лекция-беседа и т.д.
Лекционная форма проведения уроков целесообразна при:
Изучении нового материала, мало связанного с ранее изученным;
Рассмотрении сложного для самостоятельного изучения материала;
Подаче информации крупными блоками, в плане реализации теории укрупнения дидактических единиц в обучении;
Применении изученного материала при решении практических задач.
Структура лекции определяется выбором темы и цели урока.
Другими словами, лекция строится на сочетании этапов урока: организации, постановки цели и актуализации знаний; сообщении знаний учителем и усвоении их учащимися; определении домашнего задания.
Основные этапы:
|
1. Создание проблемной ситуации при постановке темы, цели и задач лекции; 2. Ее разрешение при реализации намеченного плана лекции; 3. Выделение опорных знаний и умений и их оформление с помощью памятка «Как конспектировать лекцию» 4. Воспроизведение учащимися опорных знаний и умений по образцам конспекта, блок-конспекта, опорным конспектам и т.д. 5. Применение полученных знаний; 6. Обобщение и систематизация изученного; 7. Формирование домашнего задания постановкой вопросов для самопроверки, сообщение списка рекомендуемой литературы и перечня заданий из учебника.
|
8. Урок семинар
Семинары характеризуются, прежде всего, двумя взаимосвязанными признаками: самостоятельным изучением учащимися программного материала и обсуждением на уроке результатов их познавательной деятельности. На них ребята учатся выступать с самостоятельными сообщениями, дискутировать, отстаивать свои суждения. Семинары способствуют развитию познавательных и исследовательских умений учащихся, повышению культуры общения.
Различают уроки-семинары по учебным задачам, источникам получения знаний, формам их проведения и т.д. В практике обучения получили распространение такие как:
- семинары - развернутые беседы;
- семинары – доклады;
- рефераты;
- творческие письменные работы;
- комментированное чтение;
- семинар – решение задач;
- семинар–диспут;
- семинар-конференция и т.д.
Предпочтительнее организовывать уроки в форме семинаров
при изучении нового материала, если он доступен для самостоятельной проработки учащимися;
после проведения вводных, установочных и текущих лекций;
при обобщении и систематизации знаний, умений учащихся по изучаемой теме;
при проведении уроков, посвященных различным методам решения задач, выполнения заданий и упражнений и т.д .
Семинар проводится со всем составом учащихся.
Учитель заблаговременно определяет тему, цель и задачи семинара, планирует его проведение, формулирует основные и дополнительные вопросы по теме, распределяет задания между учащимися с учетом их индивидуальных возможностей, подбирает литературу, проводит групповые и индивидуальные консультации, проверяет конспекты. Получив задание, учащиеся с помощью памяток «Как конспектировать источники», «Как готовиться к выступлению», «Как готовиться к семинару», «Памятки докладчика» оформляют результаты самостоятельной работы в виде плана или тезисов выступлений, конспектов основных источников, докладов, рефератов.
Семинарское занятие начинается вступительным словом учителя, в котором он напоминает задачу семинара, порядок его проведения, рекомендует, на что следует обратить особое внимание, что следует записать в рабочую тетрадь, дает другие советы. Далее обсуждаются вопросы семинара в форме дискуссии, развернутой беседы, сообщений, чтения первоисточников с соответствующими комментариями, докладов, рефератов и т.д.
Затем учитель дополняет сообщения учеников, отвечает на их вопросы и дает оценку выступлениям. Подводя итоги, отмечает положительное, анализирует содержание, форму выступлений учащихся, указывает на недостатки и пути их преодоления.
Проведение семинаров может быть составной частью лекционно – семинарской системы обучения, расширяющей область их применения.
9.Урок-зачет
Одной из форм организации контроля знаний, умений и навыков учащихся является урок-зачет.
Основная цель его состоит в диагностике уровня усвоения знаний каждым учащимся на определенном этапе обучения.
Практикуются различные виды зачетов:
- текущий;
- тематический;
- зачет-практикум;
- дифференцированный зачет;
- зачет-экстерн и т.д.
При проведении используются различные формы организации деятельности учителя и учащихся: зачет в форме экзамена, ринга, аукциона и т.д. Если учащимся предварительно сообщают примерный перечень заданий, выносимых на зачет, то его принято называть открытым. Чаще же предпочтение отдается открытым с целью определения результатов изучения наиболее важных тем учебного предмета.
Возможные основные этапы подготовки и проведения открытого тематического зачета.
Такой зачет проводится как завершающая проверка в конце изучаемой темы. Приступая к ее изложению, учитель сообщает о предстоящем зачете, его содержании, особенностях организации и сроках сдачи. Для проведения зачета из числа наиболее подготовленных учащихся отбираются консультанты. Они помогают распределить учащихся по группам в 3-5 человек, готовят учетные карточки для своих групп, в которых будут фиксироваться отметки за выполнение учениками каждого задания и итоговые отметки за зачет. Задания готовятся двух видов: основные, соответствующие обязательному уровню подготовки учащихся, и дополнительные, выполнение которых вместе с основными необходимо для получения хорошей или отличной отметки.
Каждому ученику (кроме консультантов) готовятся индивидуальные задания, включающие основные и дополнительные вопросы и упражнения. В начале зачета, как правило, на спаренном уроке ученику получают свои задания и приступают к их выполнению. В это время учитель проводит собеседование с консультантами. Он проверяет и оценивает их знания, а затем разъясняет методику проведения заданий.
На следующем этапе урока консультанты приступают к проверке выполнения заданий в своих группах, а учитель выборочно из разных групп проверяет в первую очередь, работы учащихся, справившихся с основными заданиями и приступивших к выполнению дополнительных заданий.
В заключительной части урока завершается оценка каждого задания выставление отметок в учетные карточки групп, учитель на основе выставленных оценок выводит итоговые отметки каждому ученику и подводит общие итоги зачета.
10.Урок-практикум
Специальная задача уроков-практикумов – усиление практической направленности обучения, но кроме этого они должны быть тесным образом связаны с изученным материалом, а также способствовать прочному, неформальному его усвоению. Основной формой их проведения являются практические и лабораторные работы, на которых учащиеся самостоятельно упражняются в практическом применении усвоенных теоретических знаний и умений.
Главное их отличие состоит в том, что на лабораторных работах доминирующей составляющей является процесс формирования экспериментальных умений учащихся, а на практических работах – конструктивных.
Различают следующие виды уроков-практикумов:
- установочные;
- иллюстративные;
- исследовательские;
- творческие;
- обобщающие.
Основным способом организации деятельности учащихся на практикумах является групповая форма работы. При этом каждая группа из двух-трех человек выполняет, как правило, отличающуюся от других практическую или лабораторную работу.
Средством управления учебной деятельностью учащихся при проведении практикума служит инструкция, которая по определенным правилам последовательно устанавливает действия учеников.
Основные этапы урока- практикума:
|
1. Сообщение темы, цели и задач практикума; 2. Актуализация опорных знаний и умений учащихся; 3.Мотивация учебной деятельности учащихся; 4. Ознакомление учеников с инструкцией; 5. Подбор необходимых дидактических материалов, средств обучения и оборудования; 6. Выполнение работы учащимися под руководством учителя; 7. Доставление отчета; 8. Обсуждение и теоретическая интерпретация полученных результатов работы.
|
11. Урок экскурсия
На уроки-экскурсии переносятся основные задачи учебных экскурсий: обогащение знаний учащихся; установление связи теории с практикой, с жизненными явлениями и процессами; развитие творческих способностей учащихся, их самостоятельности, организованности; воспитание положительного отношения к учению.
По содержанию уроки-экскурсии делятся на
- тематические (охватывающие одну или несколько тем одного предмета);
- комплексные (базируются на содержании взаимосвязанных тем двух или нескольких учебных предметов).
По времени проведения относительно изучаемых тем различают:
- вводные;
- сопутствовавшие;
- заключительные.
Форма проведения уроков-экскурсий разнообразна. Это и «пресс-конференция» с участием представителей предприятия, учреждения, музея и т.п. и исторические экскурсии по изучаемому предмету, и кино- или теле-экскурсии, и урок обобщающего повторения по теме, разделу или курсу в форме экскурсии и т.д.
Тем не менее, структурные элементы различных видов экскурсий являются в достаточной степени определенными.
Основные этапы тематического урока-экскурсии:
|
1. Сообщение темы, цели и задач урока; 2. Актуализация опорных знаний учащихся; 3.Восприятие особенностей экскурсионных объектов, первичное осознание заложенной в них информации; 4.Ообобщение и систематизация знаний; 5. Подведение итогов урока и выдача учащимся индивидуальных заданий.
|
12. Урок-дискуссия
Основа уроков-дискуссий – рассмотрение и исследование спорных вопросов, проблем, различных подходов при аргументации суждений, решении заданий и т.д.
Различают:
- дискуссии-диалоги (диалог двух ее главных участников)
- групповые дискуссии (спорные вопросы решаются в процессе групповой работы);
- массовые (в полемике участвуют все учащиеся класса).
При подготовки урока-дискуссии учитель должен четко сформулировать задание, раскрывающее сущность проблемы и возможные пути ее решения. В случае необходимости участникам предстоящей дискуссии надо ознакомиться с дополнительной литературой, заранее отобранной и предложенной учителем.
В начале урока обосновывается выбор темы или вопроса, уточняются условия дискуссии, выделяются узловые моменты обсуждаемой проблемы. Главный момент дискуссии – непосредственный спор ее участников. Для его возникновения неприемлем авторитарный стиль преподавания, ибо он не располагает к откровенности, высказыванию своих взглядов. Ведущий дискуссии (чаще всего учитель0, может использовать различные приемы активизации учащихся, подбадривая их репликами типа: «хорошая мысль», «интересный подход, но…», «давайте подумаем вместе», либо делая акцент на разъяснение смысла противоположных точек зрения и т.д. Необходимо размышлять вместе с учениками, помогая им при этом формулировать свои мысли, и развивать сотрудничество между собой и ими.
В ходе дискуссии не надо добиваться единообразия оценок. Однако по принципиальным вопросам следует вносить ясность. Особняком стоит вопрос о культуре дискуссии. Оскорбления, упреки, недоброжелательность в отношении к своим товарищам не должны присутствовать в споре. Крик, грубость чаще всего возникают тогда, когда в основе дискуссии лежат не факты или закономерности, а только эмоции. При этом часто ее участники не владеют предметом спора и «говорят на разных языках», формированию культуры дискуссии могут помочь следующие правила:
вступая в дискуссию, необходимо представлять предмет спора;
в споре не допускать тона превосходства;
грамотно и четко ставить вопросы;
формулировать главные выводы.
Момент окончания дискуссии следует выбирать так, чтобы предупредить повторение уже сказанного, ибо это отрицательно влияет на поддержание интереса учащихся к рассматриваемым на уроке проблемам. Завершив дискуссию, необходимо подвести итог: оценить правильность формулировки и употребления понятий, глубину аргументов, умение использовать приемы доказательств, опровержений, выдвижения гипотез, культуру дискуссии. На этом этапе учащиеся получают за дискуссию отметки, но при этом не надо снижать отметку за то, что ученик отстаивал неверную точку зрения.
На заключительном этапе урока можно не только систематизировать возможные пути решения обсуждаемой проблемы, но и поставить связанные с ней новые вопросы, дающие пищу для новых раздумий учащихся.
Следует отметить, что дискуссия является также одним из основных структурных компонентов урока-диспута, суда, заседания ученого совета и т.д.
13. Урок-консультация
На уроках данного типа проводится целенаправленная работа не только по ликвидации пробелов в знаниях учащихся, обобщению и систематизации программного материала, но и по развитию умений.
В зависимости от содержания и назначения выделяют:
- тематические уроки-консультации;
- целевые уроки-консультации.
Тематические консультации проводятся либо по каждой теме, либо по наиболее значимым или сложным вопросам программного материала.
Целевые консультации входят в систему подготовки, проведения и подведения итогов самостоятельных и контрольных работ, зачетов, экзаменов. Это могут быть уроки работы над ошибками, уроки анализа результатов контрольной работы или зачета и т.д.
На консультации сочетаются различные формы работы с учащимися: общие, групповые и индивидуальные.
Подготовка к проведению урока-консультации осуществляется как учителем, так и учащимися. Учитель наряду с логико-дидактическим анализом содержания изучаемого материала систематизирует затруднения, недочеты и ошибки в устных ответах и письменных работах учащихся. На этой основе он уточняет перечень возможных вопросов, которые будут рассмотрены на консультации. Ребята приучаются, в свою очередь, готовиться к консультациям, сроки которых объявляются заранее, вопросы и задания, вызывающие у них затруднения. При этом возможно использование не только учебника, но и дополнительной литературы.
Накануне урока-консультации можно предложить учащимся домашнее задание: подготовить по изучаемой теме карточки с вопросами и заданиями, с которыми они не могут справиться. Если на первых консультациях учитель не получит вопросов: он вначале предлагает учащимся открыть учебник и, анализируя объяснительный текст и имеющиеся там задания, вскрывает вопросы, которые могли бы быть заданы учениками, но ускользнули от их внимания. Затем оставшаяся часть урока, наряду с отработкой подобных умений, посвящается разбору вопросов, подготовленных учителем.
Когда ученики поймут, как готовиться к урокам-консультациям, они могут подготовить такое число вопросов, что для ответов на них не хватит времени на уроке. В таких случаях учитель либо обобщает некоторые вопросы, либо отбирает наиболее значимые из них, перенося оставшиеся вопросы на следующие уроки.
Иная ситуация возникает в случае, когда вопросы учащихся подчерпнуты из дополнительной литературы. Получая ответы на них, ученики отлично сознают, что они зачастую заранее не были известны учителю. Другими словами, ребята получают возможность заглянуть в творческую лабораторию учителя.
В ходе урока-консультации учитель получает возможность узнать учеников с лучшей стороны, пополнить сведения о динамике их продвижения, выявить наиболее любознательных и пассивных, поддержать тех, кто испытывает затруднения и помочь им. Последнее реализуется с помощью индивидуальных и групповых форм работы, где помощниками могут быть консультанты из числа учащихся, хорошо разобравшихся в вопросах по изучаемой теме.
14. Интегрированный урок
Интеграция дает возможность, с одной стороны показать учащимся «мир в целом», преодолев разобщенность научного знания по дисциплинам, а с другой стороны – высвобождаемое за этот счет учебное время использовать для полноценного осуществления профильной дифференциации в обучении.
Иначе говоря, с практической точки зрения интеграция предполагает усиление межпредметных связей, снижение перегрузок учащихся, расширение сферы получаемой информации учащимися, подкрепление мотивации обучения.
Методической основой интегрированного подхода к обучению является формирование знаний об окружающем мире и его закономерностей в целом, а также установление внутрипредметных и межпредметных связей в усвоении основ наук. В этой связи интегрированным уроком называют любой урок со своей структурой, если для его проведения привлекают знания, умения и результаты анализа изучаемого материала методами других наук, других учебных предметов. Не случайно, поэтому интегрированные уроки именуют еще межпредметными, а формы их проведения самые разные: семинары, конференции, путешествия и т.д.
Наиболее общая классификация интегрированных уроков по способу их организации входит составной частью в иерархию ступеней интеграции, которая в свою очередь, имеет следующий вид:
конструирование и проведение урока двумя и более учителями разных дисциплин;
конструирование и проведение интегрированного урока одним учителем, имеющим базовую подготовку по соответствующим дисциплинам;
создание на этой основе интегрированных тем, разделов и, наконец, курсов.
15. Театрализованный урок
Выделение такого типа уроков связано с привлечением театральных средств, атрибутов и их элементов – при изучении, закреплении и обобщении программного материала. Театрализованные уроки привлекательны тем, что вносят в ученические будни атмосферу праздника, приподнятое настроение, позволяют ребятам проявлять свою инициативу, способствуют выработке у них чувства взаимопомощи, коммуникативных умений.
Как правило, театрализованные уроки разделяют по организации:
- спектакль;
- сказка;
- студия и т.д.
При подготовке таких уроков даже работа над сценарием и изготовление элементов костюмов становятся результатом коллективной деятельности учителя и учащихся. Здесь, как и на самом театрализованном уроке, складывается демократичный тип отношений, когда учитель передает учащимся не только знания, но и свой жизненный опыт, раскрывается перед ними как личность.
Наполнение сценария фактическим материалом и его реализация на театрализованном уроке требует от учащихся серьезных усилий в работе с учебником, первоисточником, научно-популярной литературой, при изучении соответствующих исторических сведений, что, в конечном счете, вызывает у них интерес к знаниям.
На самом уроке учитель лишается роли обучающегося, ибо он выполняет лишь функции организатора представления. Оно начинается, как правило, со вступительного слова ведущего, обязанности которого не обязательно возглавлять на учителя. Само представление после информационной части может быть продолжено постановкой проблемных заданий, которые непосредственно подключают в активную работу на уроке остальных учащихся.
В заключительной части представления, еще и в стадии разработки, желательно предусмотреть этап подведения итогов и связанную с ним тщательную подборку критериев оценок, учитывающих все виды деятельности учащихся на уроке. Их основные положения должны быть заранее известны всем ребята.
Такая структура применяется как один из вариантов при конструировании театрализованных уроков, многообразие которых определяется, прежде всего, содержанием используемого, материала и выбором соответствующего сценария.
16. Урок-соревнование
Основу урока-соревнования составляют состязания команд при ответах на вопросы и в решении чередующихся заданий, предложенных учителем.
Форма проведения таких уроков самая различная.
Это поединок, эстафета, соревнования, построенные по сюжетам известных игр: КВН, «Брейн-ринг», «Счастливый случай», «Звездный час» и др.
В организации уроков – соревнований выделяют три основных этапа:
подготовительный;
игровой;
подведение итогов.
Для каждого конкретного урока эта структура детализируется в соответствии с содержанием используемого материала и особенностей сюжета состязаний.
Рассмотрим, например, специфику организации и проведения «боя» команд по учебному предмету на уроке.
Для участия в соревновании класс разбивается на две-три команды. Каждой команде даются одни и те же задания с таким расчетом, чтобы число заданий было равно числу участников команд. Выбираются капитаны команд. Они руководят действиями своих товарищей и распределяют, кто из членов команд будет отстаивать решение каждого задания в бою. Дав время на обдумывание и поиск решений, жюри, состоящее из учителя и учащихся, не вошедших в состав команд, следит за соблюдением правил соревнования и подводит итоги состязания.
Бой открывается конкурсом капитанов, который не приносит баллов, но дает той команде, капитан которой победит право осуществить вызов или передать эту возможность соперникам. В дальнейшем команды вызывают друг друга по очереди. Вызывающая команда указывает каждый раз, на какое задание она вызывает противника. Если вызов принимается, то вызванная команда выставляет участника, рассказывающего решение, а ее соперники - оппонента, ищущего в этом решении ошибки и недочеты. Если вызов не будет принят, то уже, наоборот, кто-то из членов вызывающей команды рассказывает решение, а оппонирует его член вызванной команды.
Жюри определяет баллы за решение и оппонирование каждого задания. Если никто из членов команд не знает решения, то его приводит учитель или член жюри. В конце урока подводятся командные и индивидуальные итоги. Исключительное значение в соревновании имеет объективность оценки уровня знаний. В случае правильного ответа, как отмечалось, участники и команды получают определенное количество баллов, соответствующее трудности вопроса. При неправильном же выполнении задания, списывании или подсказках снимается определенное количество баллов.
17. Урок с дидактической игрой
В отличии от игр вообще дидактическая игра обладает единственным признаком – наличием четко поставленной цели обучения и соответствующего ей педагогического результата. Дидактическая игра имеет устойчивую структуру, включающую следующие основные компоненты:
Игровой замысел выражен, как правило, в названии игры. Он заложен в той дидактической задаче, которую надо решать на уроке, и придает игре познавательный характер, предъявляет к ее участникам определенные требования в отношении знаний.
Правилами определяется порядок действий и поведения учащихся, в процессе игры, создается рабочая обстановка на уроке. Поэтому их разработка ведется с учетом цели урока и возможностей учащихся. В свою очередь, правилами игры создаются условия для формирования умений учащихся управлять своим поведением.
Регламентированные правилами игровые действия способствуют познавательной активности учащихся, дают им возможность проявить свои способности, применить знания и умения для достижения целей игры. Учитель, руководя игрой, направляет ее в нужное дидактическое русло, при необходимости активизирует ее ход, поддерживает интерес к ней.
Основой дидактической игры является познавательное содержание. Оно заключается в усвоении тех знаний и умений, которые применяются при решении учебной проблемы, поставленной игрой.
Оборудование игры в значительной мере включает в себя оборудование урока. Это и наличие технических средств обучения, и различные средства наглядности, и дидактические раздаточные материалы.
Дидактическая игра имеет определенный результат, который выступает, прежде всего, в форме решения поставленного задания и оценивания действий учащихся, придает ей законченность. Все структурные элементы игры взаимосвязаны, и при отсутствии основных из них она либо невозможна, либо теряет свою специфическую форму, превращаясь в выполнение указаний, упражнений и т.п.
Целесообразность использования дидактических игр на различных этапах урока различна. При усвоении новых знаний возможности дидактических игр уступают более традиционным формам обучения. Поэтому их чаще применяют при проверке результатов обучения, выработке навыков, формировании умений.
В этой связи различают:
-обучающие дидактические игры;
- контролирующие дидактические игры;
- обобщающие дидактические игры.
Характерной особенностью урока с дидактической игрой является включение игры в его конструкцию в качестве одного из структурных элементов урока.
Дидактические игры при их систематическое использование становятся эффективным средством активизации учебной деятельности школьников.
18. Урок - деловая игра
В деловых играх на основе игрового замысла моделируются жизненные ситуации и отношения, в рамках которых выбирается оптимальный вариант решения рассматриваемой проблемы, и имитируется его реализация на практике.
Деловые игры делятся на:
- производственные;
- организационно - деятельностные;
-проблемные;
- учебные;
- комплексные.
В рамках уроков чаще всего ограничиваются применением учебных деловых игр. Их отличительными свойствами являются:
моделирование приближенных к реальной жизни ситуаций;
поэтапное развитие игры, в результате чего выполнение предшествующего этапа влияет на ход следующего;
наличие конфликтных ситуаций;
обязательная совместная деятельность участников игры, выполняющих предусмотренные сценарием роли;
использование описания объекта игрового имитационного моделирования;
контроль игрового времени;
элементы состязательности;
правила, системы оценок хода и результатов игры.
Методика разработки деловых игр включает следующие этапы:
Обоснование требований к проведению игры;
Составление плана ее разработки;
Написание сценария, включая правила и рекомендации по организации игры;
Подбор необходимой информации;
Уточнение целей проведения игры, составление руководства для ведущего, инструкций для игроков; дополнительный подбор и оформление дидактических материалов;
Разработка способов оценки результатов игры в целом и ее участников в отдельности.
Возможные варианты структуры деловой игры на уроке:
|
1. Знакомство с реальной ситуацией; 2. Построение ее имитационной модели; 3. Постановка главной задачи командам (бригадам, группам), уточнение их роли в игре; 4. Создание игровой проблемной ситуации; 5. вычленение необходимого для решения проблемы теоретического материала; 6. Решение проблемы; 7. Обсуждение и проверка полученных результатов; 8. Коррекция; 9. Реализация принятого решения; 10. Анализ итогов работы; 11. Оценка результатов работы. |
19. Урок – ролевая игра
Специфика ролевой игры, в отличии от деловой, характеризуется более ограниченным набором структурных компонентов, основу которых составляют целенаправленные действия учащихся в моделируемой жизненной ситуации в соответствии с сюжетом и распределенными ролями.
Уроки – ролевые игры можно разделить по мере возрастания их сложности на три группы:
- имитационные, направленные на имитацию определенного профессионального действия;
- ситуационные, связанные с решением какой-либо узкой конкретной проблемы – игровой ситуации;
- условные, посвященные разрешению, например, учебных или производственных конфликтов и т.д.
Формы проведения ролевых игр могут быть самыми разными: воображаемые путешествия; дискуссии, на основе распределения ролей, пресс-конференции и т.д.
Методика разработки и проведения ролевых игр предусматривает включение в полной мере или частично следующих этапов:
Подготовительный;
Игровой;
Заключительный;
Анализ результатов.
На подготовительном этапе решаются вопросы как организационные, так и связанные с предварительным изучение содержательного материала игры:
Распределение ролей;
Выбор жюри или экспертной группы;
Формирование игровых групп;
Ознакомление с обязанностями.
Предваряющие вопросы:
Знакомство с темой, проблемой;
Ознакомление с инструкциями, заданиями;
Сбор материала, анализ материала, подготовка сообщения;
Изготовление наглядных пособий;
Консультации.
Игровой этап характеризуется включением в проблему и осознанием, проблемной ситуации в группах и между группами.
Внутригрупповой аспект: индивидуальное понимание проблемы; дискуссия в группе; выявление позиций; понятие решения; подготовка сообщения.
Межгрупповой аспект: заслушивание сообщений групп; оценка решения.
На заключительном этапе вырабатываются решения по проблеме, заслушивается сообщение экспертной группы, выбирается наиболее удачное решение. При анализе результатов ролевой игры определяется степень активности участников, уровень знаний и умений, вырабатываются рекомендации по совершенствованию игры. Проведение ролевой игры, как и всякой другой, построенной на использовании имитации, связано с преодолением трудностей, заложенных в ее противоречивом характере. Противоречивость ролевой игры заключается в том, что в ней всегда должны иметь место и условность, и серьезность. Кроме того, она проводится в соответствии с определенными правилами, предусматривающими элементы импровизации. Если хотя бы один из этих факторов отсутствует, игра не достигает цели. Она превращается в скучную инсценировку в случае излишней регламентации и отсутствия импровизации или в фарс, когда играющие утрачивают серьезность и их импровизации носят абсурдный характер.
4. Разработки некоторых типов уроков.
1. Комбинированный урок
Тема урока: Положительные и отрицательные числа.
Цели урока: формирование базовой математической подготовки.
Задачи:
образовательные: ввести понятия положительных и отрицательных чисел их обозначение, научить читать отрицательные числа, показать применение положительных и отрицательных чисел;
развивающие: развитие логического мышления, памяти; способствовать умению наблюдать, анализировать, сравнивать и делать соответствующие выводы.
воспитательные: воспитание культуры труда, продолжить формирование познавательного интереса к предмету.
Формы организации учебно-познавательной деятельности:
Индивидуальная
групповая
фронтальная
Методы обучения:
наглядный
словесно-иллюстративный
репродуктивный
практический
Технологии:
Оборудование:
Ход урока
I. Организационный момент (2 мин)
II. Подготовка к восприятию нового материла (7мин)
Для подготовки к восприятию нового материала используется два вида работы: фронтальная и групповая.
1. Групповая работа (работают три группы по карточкам)
Задание: Перед вами множество чисел:
14, - 8; 4
; 3,5; 72; -13; 0,68; 
; -25; 102; 5,324; 12
Задание 1 группе: Выписать натуральные числа.
Задание 2 группе: Выписать десятичные дроби.
Задание 3 группе: Выписать обыкновенные дроби.
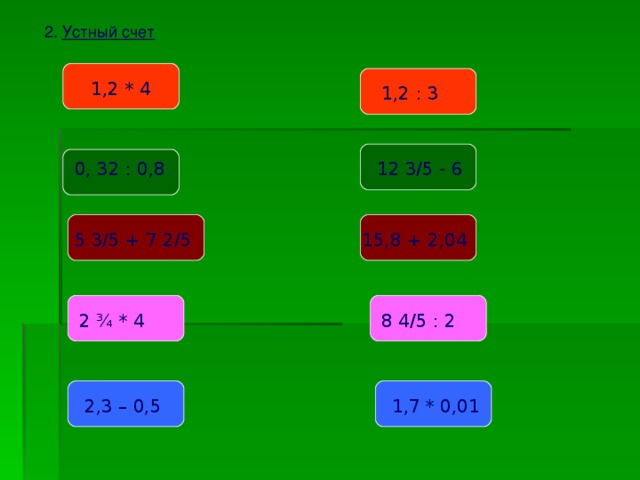
2. Фронтальная работа (устный счет с использованием презентации)
1. 1,2 ∙ 4
2. 0,32 : 0,8
3. 5
+ 7
4. 2
∙ 4
5. 2,3 – 0, 5
6. 1,2 : 3
7. 12 – 6
8. 15,8 + 2,04
9. 8 : 2
10. 1,7 ∙ 0,01
III. Изучение нового материала (10 мин)
Изучение материала проводится в форме эвристической беседы.
1. Проверить выполнение задания, выполняемого группами.
- Какие числа отнесли к 1 группе?
-Какие числа отнесли ко второй группе?
-Какие числа отнесли к третьей группе?
- У нас остались числа: -8; -13, -25. Эти числа не относятся ни к одной из данных групп?
- Чем они отличаются от натуральных чисел? (знаком)
- Числа, получаемые из натуральных чисел приписыванием знака «-« называются отрицательными.
- У вас наверно возникли вопросы:
Где встречаются отрицательные числа?
Для чего они нужны?
Кто ввел в обращение эти числа?
2. Применение отрицательных чисел (фронтальная работа с применением презентации)
а)
15 градусов тепла
15 градусов выше нуля
+15º,С (плюс 15º,С)
5 градусов мороза
5 градусов ниже нуля
-5о,С (минус 5о,С)
0º,С
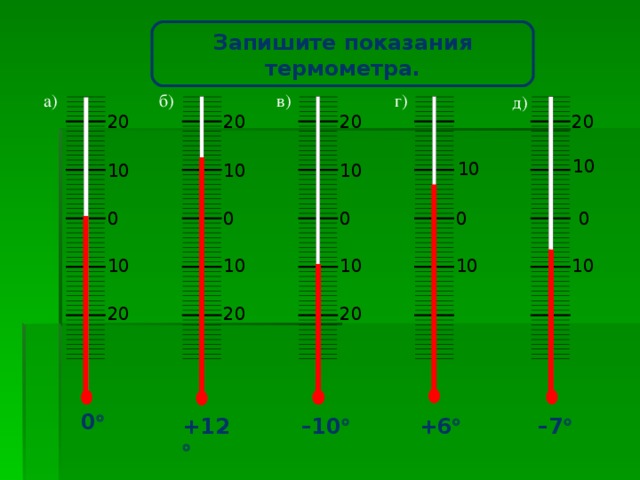
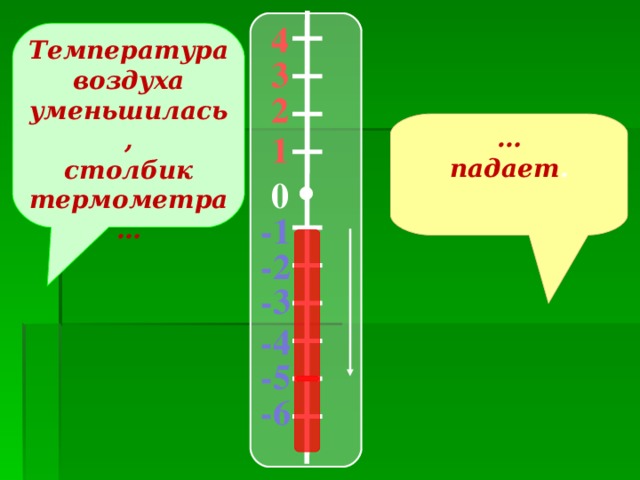
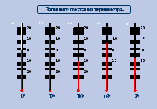Задание : Запишите показания термометра (работа в тетрадях)
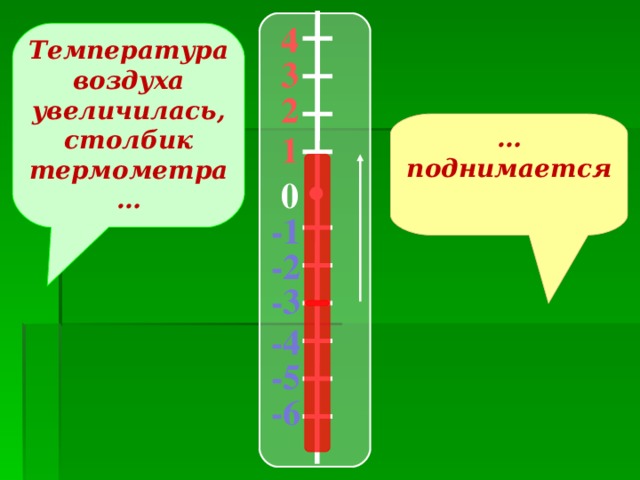
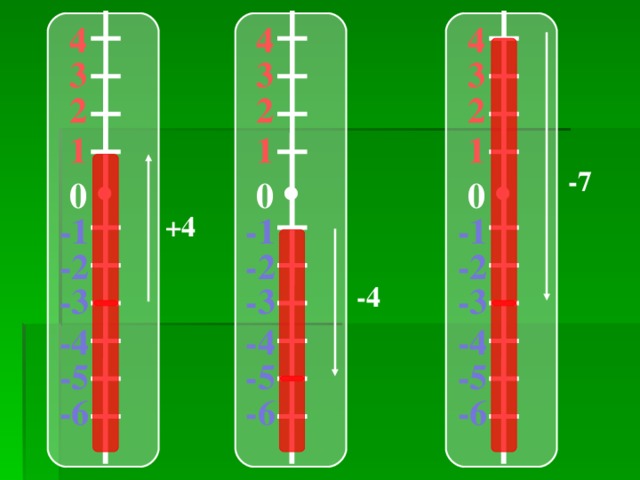
-Посмотрим, что происходит со столбиком термометра при повышении температуры воздуха и при понижении температуры воздуха.
б) Обозначение глубины озера.
Вывод (делают учащиеся под руководством учителя)
Положительные и отрицательные числа нужны в тех случаях, когда величина может изменяться в двух противоположных направлениях.
Увеличение величины выражается положительным числом, а уменьшение – отрицательным.
3. Историческая справка (сообщение учащегося)
Отрицательные числа появились значительно позже натуральных чисел и обыкновенных дробей.
Первые сведения об отрицательных числах встречаются у китайских математиков во IIв. до н.э.
Положительные числа тогда толковались как имущество, а отрицательные - как долг, недостача.
Но ни египтяне, ни вавилоняне, ни древние греки отрицательных чисел не знали. Лишь в VIIв. индийские математики начали широко использовать отрицательные числа, но относились к ним с недоверием.
В Европе отрицательными числами начали пользоваться с XII-XIII вв., но до XVIв., как и в древности, они понимались как долги, большинство ученых считали их «ложными», в отличие от положительных чисел – «истинных».
Признание отрицательных чисел способствовали работы французского математика, физика, философа. Он предложил геометрическое истолкование положительных и отрицательных чисел – ввел координатную прямую.
РЕНЕ ДЕКАРТ
ЯН ВИДМАН - чешский математик. Ввел для обозначения положительных и отрицательных чисел знаки «+» и «-».
III. Закрепление нового материала (18 мин)
1. Отработка навыка записи целых чисел, для этого выполняем следующие задания:
1) №714 –задание выполняют самостоятельно в тетрадях с последующей взаимопроверкой.
2)Задание №2. Выпишите данные числа в две группы: положительные и отрицательные числа. Какое из них не вошло ни в одну группу? (задание выполняют самостоятельно в тетрадях с последующей фронтальной проверкой)
-15; 7; 28; -41; 0; 352; -591; - 999; 2000.
2. Отработка умения изображать отрицательные и положительные числа
№712 – задание выполняют в тетрадях самостоятельно, с последующей проверкой с помощью презентации.
3. Задание: Восстановите предложения (пропедевтика обучения)- фронтальная работа с помощью презентации.
Температура воздуха была 100С, а стала 70С, значит, она изменилась на …………………………
Температура воздуха была 80С, а потом изменилась на +40С, значит стала ………………….
Температура воздуха изменилась на -50С и стала 190С, значит была ………………………………..
4. №715(а) – задание выполняют фронтально, с полным объяснением.
№715 (б) – задание один ученик выполняет у доски, а остальные в работают в тетрадях.
№715 (в) - задание выполняют фронтально, с полным объяснением.
5. №721- решение оформляется в тетради в виде таблицы, проверяется с использованием презентации.
IV. Итог урока (2 мин)
а) Фронтальная работа
Какие числа являются положительными? Отрицательными?
Положительным или отрицательным числом является нуль?
Для чего нужны отрицательные числа?
Как записывают положительные и отрицательные числа?
б) Оценка деятельности учащихся
V. Задание на дом (1 мин)
П.8.1
№711,
№713
2. Урок изучения нового материала
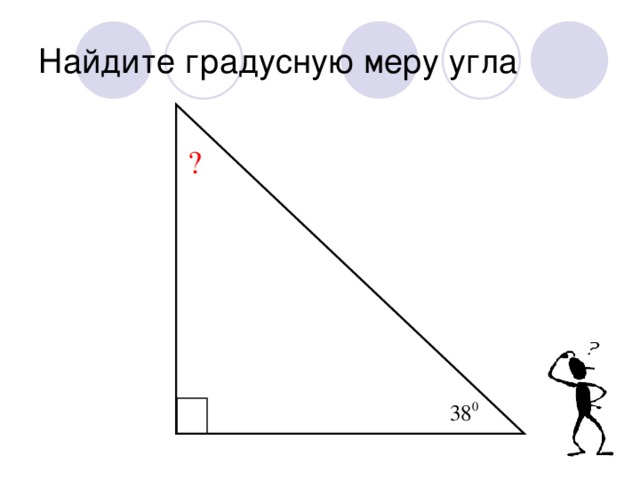
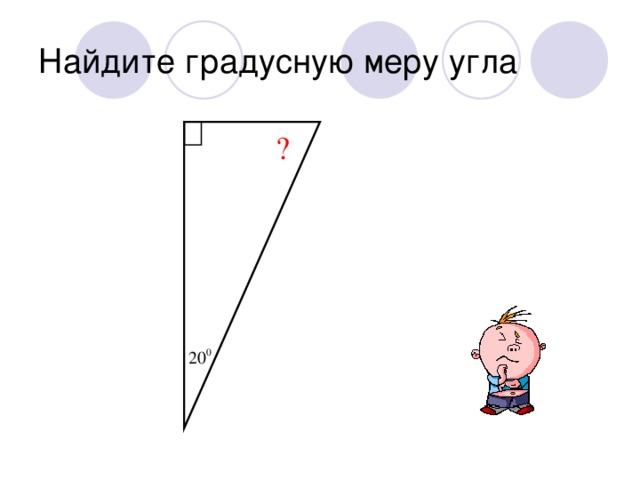
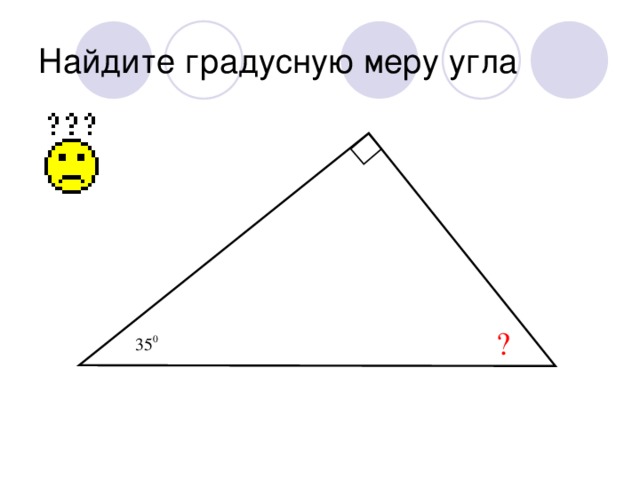
Тема урока: Сумма углов треугольника
Цели урока: формирование базовой математической подготовки.
Задачи:
образовательные: доказательство теоремы о сумме углов треугольника, следствий из неё; введение понятия остроугольного, прямоугольного и тупоугольного треугольников;
развивающие: развитие логического мышления, памяти; способствовать умению наблюдать, анализировать, сравнивать и делать соответствующие выводы.
воспитательные: воспитание культуры труда, продолжить формирование познавательного интереса к предмету.
Формы организации учебно-познавательной деятельности:
Индивидуальная
групповая
фронтальная
Методы обучения:
наглядный
словесно-иллюстративный
репродуктивный
практический
Технологии:
Оборудование:
компьютер;
мультимедийный проектор;
экран;
презентация к уроку «Сумма углов треугольника»
карточки для фронтальной работы по теме «Параллельные прямые»
таблицы для индивидуальной работы по теме «Параллельные прямые»
карточки – задания для групповой работы по теме «Сумма углов треугольника»
Ход урока
I. Организационный момент (2 мин)
II. Подготовка к восприятию нового материла (10мин)
а) Работа 1 учащегося у доски (индивидуальная работа):
Задание:
| Параллельны ли прямые а и b?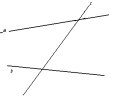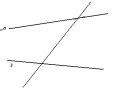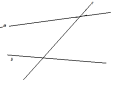   
|
б) Работа группы (с последующей проверкой у доски).
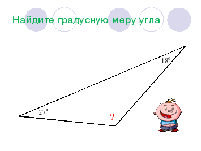
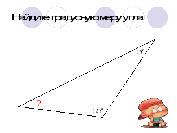
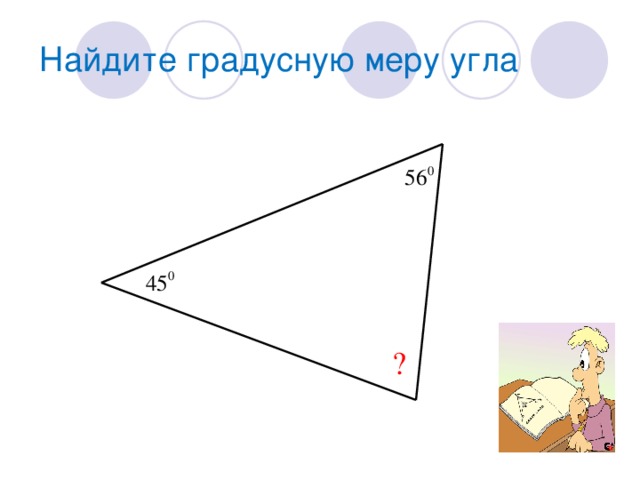
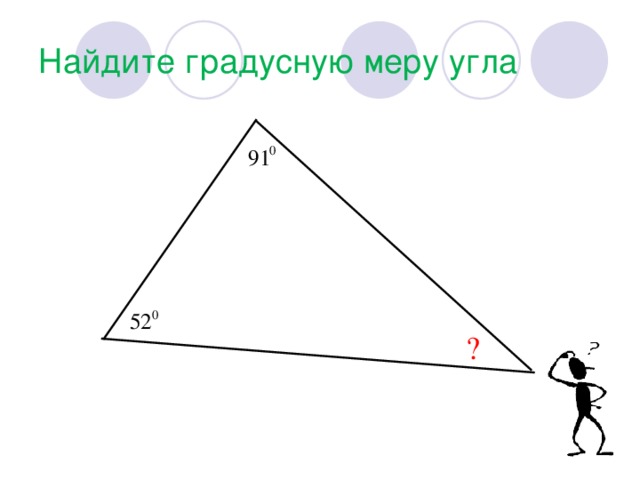
Задание:
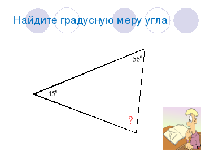
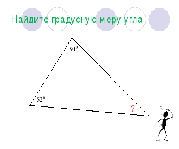
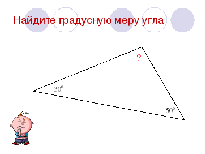
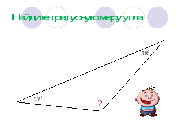
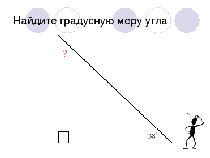
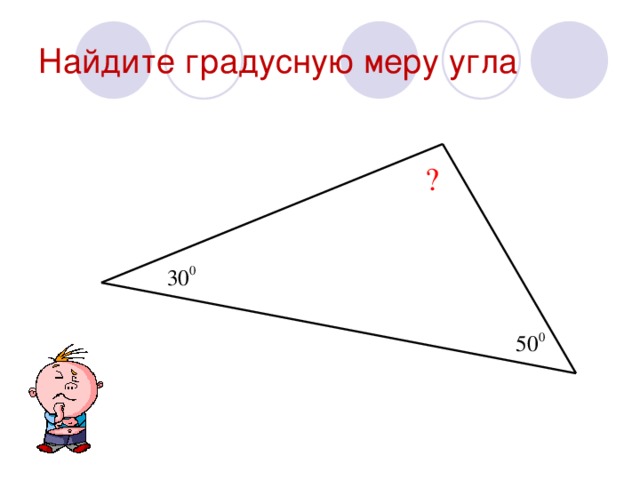
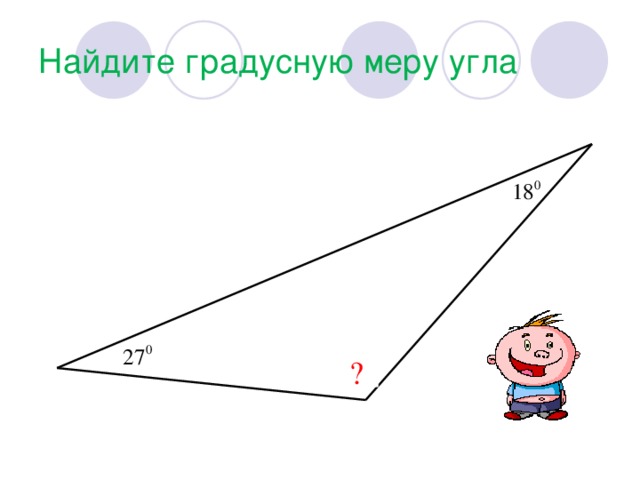
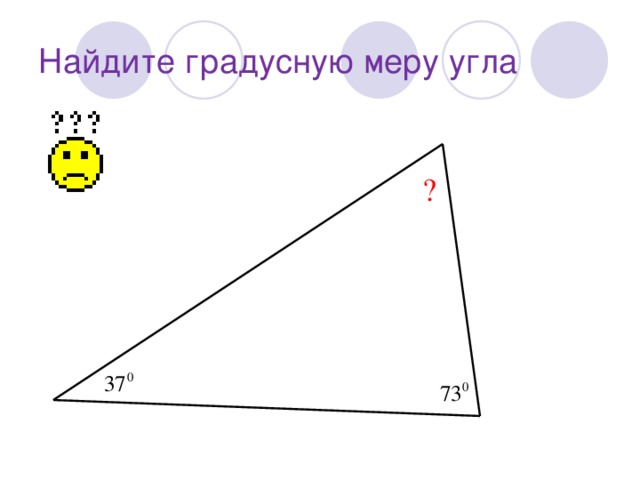
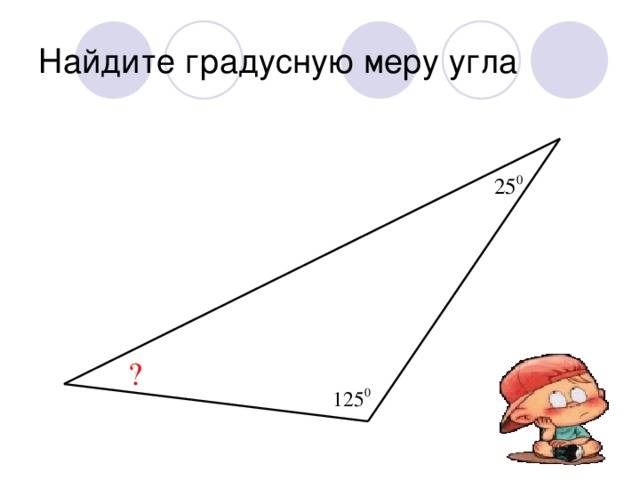
| Найти градусную меру угла 1: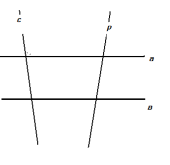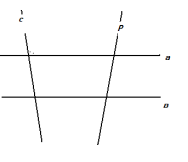  
|
в) Фронтальная работа.
Устный опрос:
1. Дать определение угла.
2. Какие виды углов существуют? Показать с помощью двух карандашей.
3. Определить вид угла по заданной его градусной мере (карточки с указанием градусных мер):
| 37° |
| 125° |
| 111° |
| 90° |
| 180° |
| 1° |
| 15° |
| 91° |
| 145° |
| 34° |
Дать определение параллельных прямых.
5.Виды углов, образованных при пересечении двух прямых секущей. Указать на чертеже:
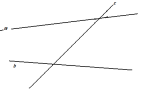
6. Сформулировать признаки параллельности прямых.
7. Сформулировать теоремы, обратные признакам параллельности прямых.
8. Сформулировать аксиому параллельных прямых.
III. Изучение нового материала (15 мин)
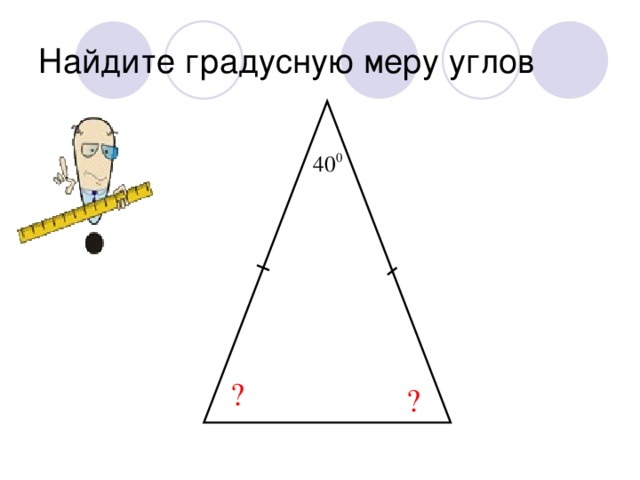
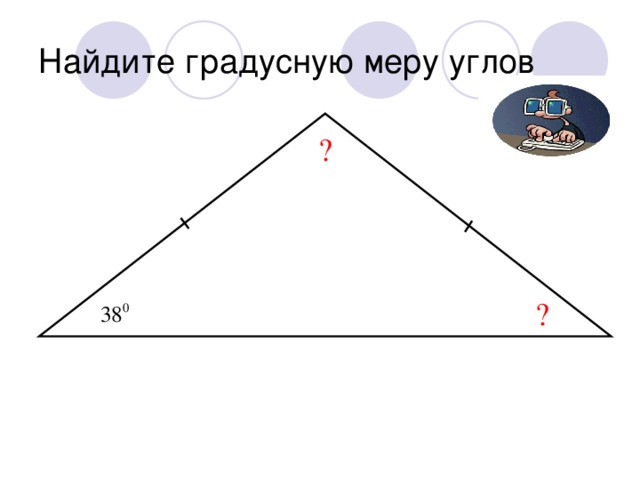
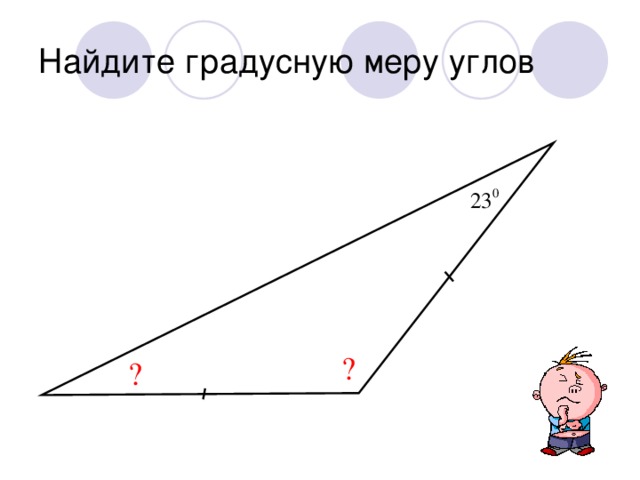
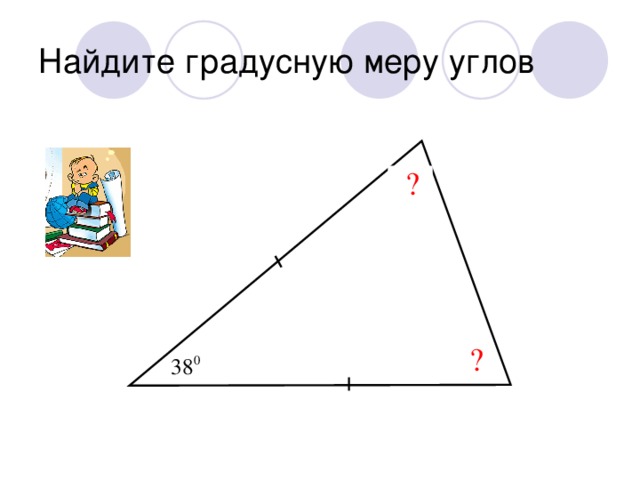
Теорема о сумме углов треугольника: «Сумма углов треугольника равна 180°»
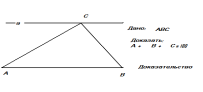
(Слайд )
Через вершину С проведём прямую а, параллельную стороне АВ.
Введём углы 1, 2, 3, 4, 5.
∠1 = ∠4 как накрест лежащие углы при параллельных прямых АВ и а и секущей АС.
∠3=∠5 как накрест лежащие углы при параллельных прямых АВ и а и секущей ВС.
∠1, ∠2, ∠3 образуют развёрнутый угол, градусная мера которого равна 180° , поэтому ∠1 + ∠2 + ∠3 =180° , отсюда следует что ∠А + ∠В + ∠С =180°.
2) Следствия из теоремы.
Формулировке следствий из теоремы о сумме углов треугольника предшествует работа групп над решением следующих проблем:
| Проблема 1: Может ли треугольник иметь два тупых угла? (вопрос группе 1)
|
| Проблема 2: Может ли треугольник иметь два прямых угла? (вопрос группе 2)
|
| Проблема 3: Может ли треугольник иметь один прямой и один тупой углы? (вопрос группе 3)
|
Ответы должны быть обоснованы с помощью теоремы о сумме углов треугольника.
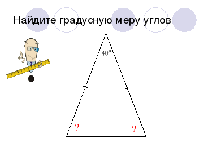
3 пары в это время отвечают на следующий вопрос: «Существует ли треугольник с такими углами?» Определить вид треугольника. (карточки – задания для каждой пары с пятью тройками углов):
| 40°, 40°, 40° | 100°, 45°, 35° | 50°, 40°, 90° | 86°, 31°, 63° | 123°, 47°, 50° |
| 150°, 50°, 50° | 130°, 45°, 5° | 150°, 40°, 10° | 55°, 45°, 80° | 23°, 90°, 67° |
| 60°, 60°, 60° | 140°, 20°, 20° | 47°, 80°, 43° | 90°, 10°, 80° | 120°, 68°, 7° |
После ответов первых трёх групп формулируются следствия из теоремы:
В треугольнике:
все три угла острые (остроугольный треугольник);
два угла острые, а третий – прямой (прямоугольный треугольник);
два угла острые, а третий – тупой (тупоугольный треугольник).
Показ моделей всех видов треугольников по углам.
Закрепление изученного материала. Решение задач (13̒)
а) Проверка ответов трёх пар, решающих задачу о существовании треугольника с данным набором углов.
б) Презентация «Сумма углов треугольника» Геометрия 7 класс.
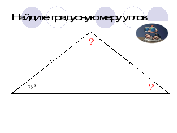
Задачи на нахождение неизвестных углов треугольника. Работа по готовым чертежам. Учащиеся выполняют вычисления в тетради с последующей проверкой правильности решения.
в) №226(устно), №228(в).
Подведение итогов урока
а) Фронтальная работа
С какой теоремой вы сегодня познакомились на уроке?
Сформулируйте эту теорему.
С какими видами треугольников познакомились на уроке?
б) Оценка работы учащихся
Задание на дом
§1 главы 4. №223(а,б), №224, №228(а).
3. Повторительно-обобщающий урок
Тема урока: Длина окружности и площадь круга
Цели урока: формирование базовой математической подготовки.
Задачи:
образовательные: обобщить и систематизировать знания по теме «Длина окружности и площадь круга;
развивающие: развитие логического мышления, памяти; способствовать умению наблюдать, анализировать, сравнивать и делать соответствующие выводы.
воспитательные: воспитание культуры труда, продолжить формирование познавательного интереса к предмету.
Формы организации учебно-познавательной деятельности:
Индивидуальная
групповая
фронтальная
Методы обучения:
наглядный
словесно-иллюстративный
репродуктивный
практический
Технологии:
Оборудование:
Ход урока
I. Организационный момент.
II. Повторение, обобщение, систематизация знаний
- Ребята, сегодня у нас повторительно-обобщающий урок по теме «Длина окружности и площадь круга. (СЛАЙД 1).
- И этот урок мне хочется начать со слов, которые являются эпиграфом к нашему уроку (СЛАЙД 2)
«Теория без практики мертва или бесплодна.
Практика без теории невозможна или пагубна.
Для теории нужны знания, для практики, сверх всего того, и умения”
А. Н. Крылов
- И сегодня мы с вами должны повторить весь теоретический материал по теме «Длина окружности и площадь круга» и закрепить умения применять его на практике для решения задач.
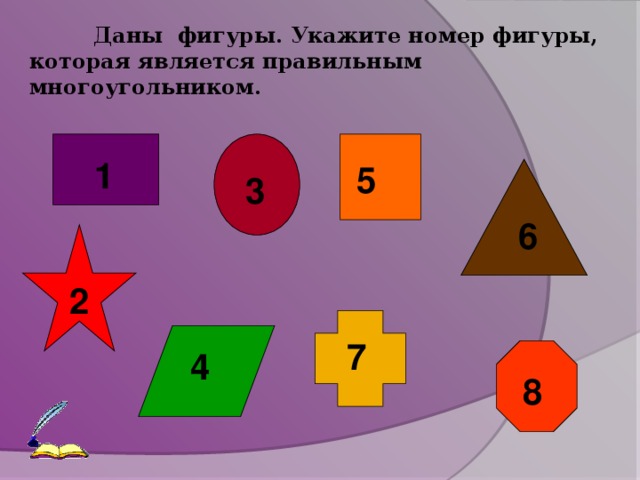
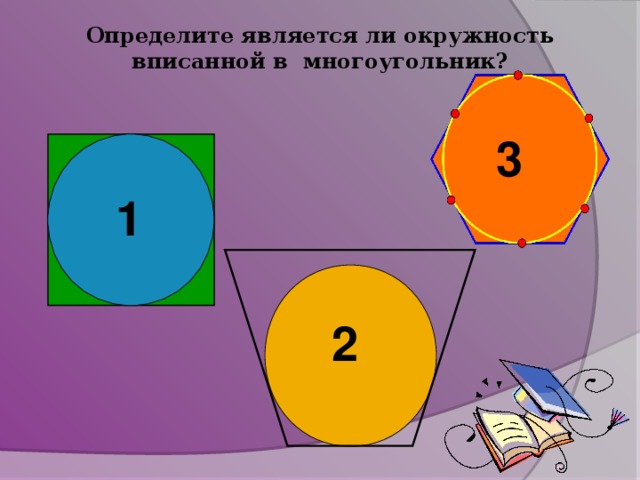
Индивидуальная работа (СЛАЙД 3)
Карточка №1:
Задание: «Вписать в окружность правильный шестиугольник»
Карточка №2:
Задание: «Описать около окружности правильный пятиугольник»
Карточка №3:
Задание:
Дано: R = 4
Найти: r, a , P, S
Карточка №4:
Задание:
Дано: r = 2
Найти: a , R,P, S
Карточка №5:
Задание:
Дано: a = 6
Найти: r, R,P, S
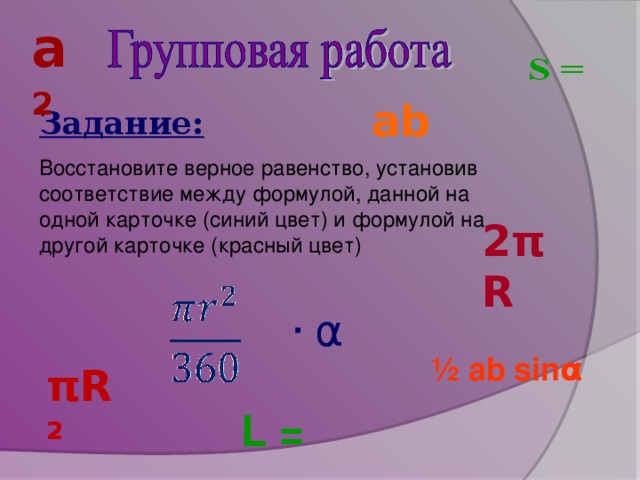
Групповая работа (Слайд 4)
Задание:
Восстановите верное равенство, установив соответствие между формулой, данной на одной карточке (синий цвет) и формулой на другой карточке (красный цвет)
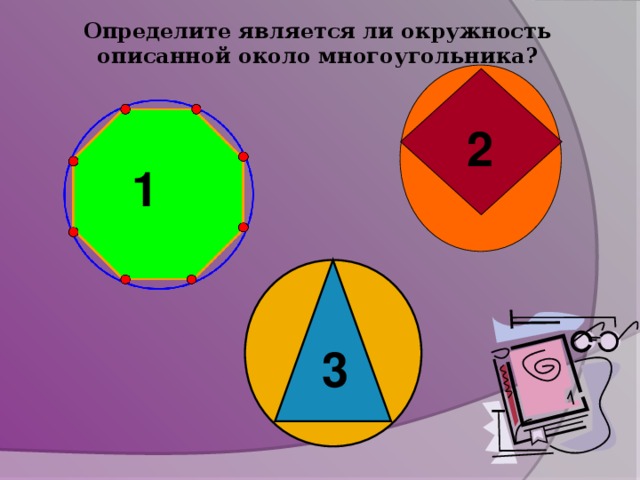
Фронтальная работа (СЛАЙД 5 – 8)
Сообщения учащихся по теме «Правильные многоугольники в нашей жизни» (Слайд 9)
Практическая работа. (Работа в группах) (СЛАЙД 12 – 17)
Задание:
Найти площадь комбинированной фигуры. (После выполнения задания представитель каждой группы выходит к доске и «Защищает» свою работу.)
Решение текстовых задач. (Работа в парах) (СЛАЙД 18 - 19)
| ВАРИАНТ 1 | ВАРИАНТ 2 |
|
Диаметр цирковой арены равен 13 м. Найдите радиус и длину окружности цирковой арены.
|
Диаметр основания царь-колокола, находящегося в Московском Кремле равен 6,6 м. Найдите радиус и площадь основания царь колокола.
|
| ВАРИАНТ 3 | ВАРИАНТ 4 |
|
Длина окружности цирковой арены равна 41 м. Найдите диаметр и площадь арены.
|
Радиус закругления пути железнодорожного полотна равен 5 км, а длина дуги закругления – 400 м. Какова градусная мера дуги закругления?
|
| ВАРИАНТ 5 | ВАРИАНТ 6 |
|
За два оборота по круговой орбите вокруг Земли космический корабль проделал путь в 84152 км. На какой высоте над поверхностью Земли находится корабль, если радиус Земли равен 6370 км?
|
С вала сняли слой стружки толщиной 0,5 см. Найдите длину окружности вала до обработки, если длина окружности вала после обработки стала равной 28,25 см.
|
III. Рефлексия: (СЛАЙД 20)
Все понятно, интересно, полезно. Я активно работал.
Интересно, но я мало работал
Мне было совсем не интересно, я не работал
IV. Домашнее задание (СЛАЙД 21)
V. Итог урока.
Спасибо! Урок окончен! (СЛАЙД 22)
4. Урок – путешествие
Тема урока: Путешествие по Галактике «Целые числа»
Цели урока: формирование базовой математической подготовки.
Задачи:
образовательные: обобщить и систематизировать знания о целых числах, закрепить и усовершенствовать навыки действий с целыми числами;
развивающие: развитие логического мышления, памяти, навыки устного счета; способствовать умению наблюдать, анализировать, сравнивать и делать соответствующие выводы.
воспитательные: воспитание культуры труда, продолжить формирование познавательного интереса к предмету.
Формы организации учебно-познавательной деятельности:
Индивидуальная
групповая
фронтальная
Методы обучения:
наглядный
словесно-иллюстративный
репродуктивный
практический
Технологии:
Оборудование:
ХОД УРОКА
1. Организационный момент
Приветствие, проверка готовности к уроку
2. Повторение, обобщение, систематизация знаний.
- Ребята, сегодня у нас необычный урок. А именно урок – путешествие, путешествие по Галактике «Целые числа» (СЛАЙД 1).
Вот уже несколько уроков подряд мы с вами находимся на планете «Целые числа». Мы познакомились с понятием целого числа, познакомились с правилами действий над целыми числами, и сегодня пришло время нам всем вместе вернуться на нашу планету «Земля».
Наш путь будет проходить через планеты: Планета «Решай-ка», Планета «Сосчитай-ка», планета «Угадай-ка», Планета «Отдыхай-ка», Планета «Сравнения», Планета «Проверяй-ка» (СЛАЙД 2). Прежде чем попасть на какую-то из этих планет мы с вами должны будем выполнить задание.
Свое путешествие мы будем совершать на космическом корабле (СЛАЙД 3).
В ПУТЬ!
Задание. Перед вами множество чисел:
¾ ; + 1; - 2,1; 0; 6; 7/3 ; 2 ½ ; - 100; 3,05; - 7; - 6; + 2,1
выберите из этих чисел целые;
какие из них натуральные?
какие из них положительные?
какие из них отрицательные?
к каким числам относится 0?
назовите пары противоположных чисел.
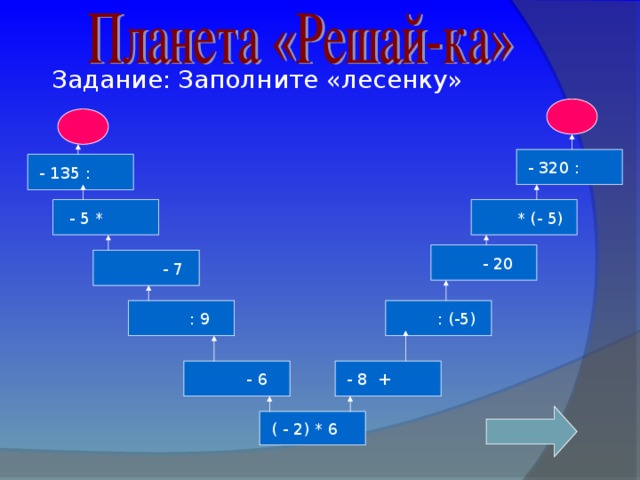
Задание. Заполните «лесенку»
- 320 :
- 135 :
∙ (- 5)
- 5 ∙
-20
- 7
: (- 5)
: 9
-8 +
- 6
(-2) ∙ 6
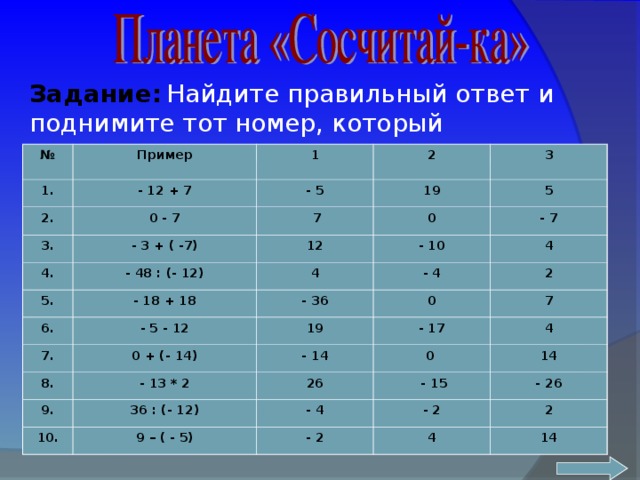
Задание: Найдите правильный ответ и поднимите тот номер (1, 2 или 3), который соответствует правильному ответу.
| № | Пример | 1 | 2 | 3 |
| 1. | - 12 + 7 | - 5 | 19 | 5 |
| 2. | 0 - 7 | 7 | 0 | - 7 |
| 3. | - 3 + (-7) | 12 | - 10 | 4 |
| 4. | - 48 : (-12) | 4 | - 4 | 2 |
| 5. | - 18 + 18 | - 36 | 0 | 7 |
| 6. | -5 - 12 | 19 | - 17 | 4 |
| 7. | 0 + (-14) | - 14 | 0 | 14 |
| 8. | - 13 ∙ 2 | 26 | - 15 | - 26 |
| 9. | 36 : (-12) | - 4 | - 2 | 2 |
| 10. | 9 – ( -5) | - 2 | 4 | 14 |
Задание: Подобрать число и вписать его в клетку так, чтобы получилось верное равенство.
1 группа 2 группа 3 группа
а) 8 + = 5 а) (-2) + = - 12 а) - 6 + = 5
б) ∙ (-12) = -24 б) ∙ ( - 8) = 64 б) ∙ 13 = - 26
в) 5 - = 10 в) - 6 = 11 в) 8 - = 14
г) – 48 : = - 24 г) – 64 : = 16 г) : (-2) = 14
ПЛАНЕТА «ОТДЫХАЙ-КА» - физминутка (СЛАЙД 3, гиперссылка на планету)
ПЛАНЕТА СРАВНЕНИЯ - Работа в парах (учащиеся выполняют задание в парах, а два представителя выполняют это же задание с обратной стороны доски) (СЛАЙД 8)
Задание. Вычислите и ответы расположите в
а) порядке возрастания
б) порядке убывания
а) – 24 + (- 5)
б) – 8 * (- 9)
в) – 96 + 96
г) – 84 : 6
д) – 32 + 38
е) 5 – 18
ж) – 7 * 3
з) 5 – (- 12)
а) 27 + (- 43) =
б) – 32 : 4 =
в) – 56 – 9 =
г) 15 * ( - 4) =
д) – 14 + (- 6) =
е) – 52 + 70 =
ж) – 120 : (- 40) =
з) – 35 – ( - 40) =
и) – 34 + (- 48) =
к) – 18 * ( - 4) =
| Количество плюсов | Оценка |
| 10 | «5» |
| 9 | «4» |
| 8 – 6 | «3» |
| Менее 6 | «2» |
Задание. Решите примеры и сопоставьте их ответы с соответствующими буквами
а) – 6 + (- 8)
б) 5 – 12
в) – 9 * (- 5)
г) 18 : (- 2)
д) 13 + (- 13)
е) 12 * ( - 4)
ж) – 8 – (- 4)
з) – 20 – 25
и) – 45 : 15
к) 20 + (- 9)
л) – 28 * 2
м) 38 – 64
н) – 16 + 25
о) + 6 + (- 14)
| Ответ | Буква |
| - 26 | Е |
| - 48 | Р |
| - 9 | З |
| - 14 | С |
| 45 | О |
| - 56 | И |
| 0 | В |
| - 7 | В |
| - 45 | Щ |
| + 9 | М |
| - 3 | Е |
| 18 | Н |
| 8 | ! |
| - 4 | А |
|
|
|
ОТВЕТ: С ВОЗВРАЩЕНИЕМ !
3. Рефлексия: (СЛАЙД 12)
Все понятно, интересно, полезно. Я активно работал.
Интересно, но я мало работал
Мне было совсем не интересно, я не работал
7. Домашнее задание. (СЛАЙД 13)
Повторить правила сложения, вычитания, умножения и деления целых чисел.
Повторить правило сравнения целых чисел
8. Итог урока.
Спасибо! Урок окончен! (СЛАЙД 14)
5. Урок - зачет
Тема урока: Правильные многоугольники
Цели урока: формирование базовой математической подготовки.
Задачи:
образовательные: проверить качество усвоения темы «Правильные многоугольники»;
развивающие: развитие логического мышления, памяти; способствовать умению наблюдать, анализировать, сравнивать и делать соответствующие выводы.
воспитательные: воспитание культуры труда, продолжить формирование познавательного интереса к предмету.
Формы организации учебно-познавательной деятельности:
Методы обучения:
наглядный
словесно-иллюстративный
репродуктивный
практический
Оборудование:
таблицы с формулами;
билеты с заданиями;
карточки с фигурами;
лист учета знаний;
Ход урока
I. Организационный момент.
II. Проведение зачета.
1 этап Проверка знания формул.
Задание: Записать недостающую часть формулы
Вариант 1 Вариант 2
аn= 1) r =
Sсек = 2) l =
=2ПR 3) =ПR2
= 
4) =
Pr
2 этап Проверка умения вписывать в окружность правильные многоугольники и описывать около окружности правильные многоугольники (ученики «вытягивают» билетики)
Задания: Б-1. Вписать в окружность правильный пятиугольник.
Б-2. Описать около окружности правильный шестиугольник.
Б-3. Вписать в окружность правильный восьмиугольник.
Б-4. Описать около окружности правильный пятиугольник.
Б-5. Вписать в окружность правильный десятиугольник.
Б-6. Описать около окружности правильный восьмиугольник.
3 этап Проверка умения находить площади комбинированных фигур (учитель сам раздает карточки учащимся)
Задание: Выполнив необходимые измерения найти площадь закрашенной фигуры.
4 этап Проверка умения решать задачи на применение формул (ученики сами выбирают ту задачу, которую они могут решить)
а) связывающих сторону правильного многоугольника с радиусом описанной окружности;
б) связывающих радиус вписанной окружности с радиусом описанной окружности;
в) площади правильного многоугольника;
Вариант 1. на «3»
Дано: R = 4
Найти: r, a4, P, S
Вариант 2. на «4»
Дано: a4 = 6
Найти: r, R, P, S
Вариант 3. на «5»
Дано: r = 2
Найти: r, a4, P, S
5 этап Проверка умения решать задачи практического характера.
Вариант 1. Задача, соответствующая требованию обязательных результатов обучения.
Задача: Длина окружности цирковой арены равна 41 м. Найдите диаметр и площадь арены.
Вариант 2. Задача для учащихся со средним уровнем знания геометрии.
Задача: Вокруг круглой клумбы, радиус которой равен 3 км проложена дорожка шириной 1 м. Сколько нужно песка, чтобы посыпать дорожку, если на 1 м2 дорожки требуется 0,8 дм3 песка?
Вариант 3. Задача для учащихся, которые имеют «5» по геометрии.
Задача: За два оборота по круговой орбите вокруг Земли космический корабль проделал путь в 84152 км. На какой высоте над поверхностью Земли находится корабль, если радиус Земли равен 6370 км?
III. Итог урока
Итоги зачета подводятся на следующем уроке.
Лист учета знаний
| Ф.И. | 1 этап | 2 этап | 3 этап | 4 этап | 5 этап | Итог |
| Сулейманова Л | 5 | 4 | 5 | 4 | 3 | 4 |
6. Урок – практикум
Тема урока: Решение задач по теме «Площадь. Теорема Пифагора»
Цели урока: формирование базовой математической подготовки.
Задачи:
образовательные: отработать навыки решения задач на нахождение площади многоугольника и применение теоремы Пифагора;
развивающие: развитие логического мышления, памяти, способствовать умению наблюдать, анализировать, сравнивать и делать соответствующие выводы.
воспитательные: воспитание культуры труда, продолжить формирование познавательного интереса к предмету.
Формы организации учебно-познавательной деятельности:
Методы обучения:
Оборудование:
карточки для фронтальной работы;
карточки для групповой работы;
лист учета решенных задач;
Ход урока
I. Организационный момент.
II. Актуализация знаний.
а) Индивидуальная работа у доски
Задания:
Начертить прямоугольник и сделав необходимые измерения найти его площадь.
Начертить треугольник и сделав необходимые измерения найти его площадь.
Начертить ромб и сделав необходимые измерения найти его площадь.
Начертить трапецию и сделав необходимые измерения найти его площадь.
Начертить квадрат и сделав необходимые измерения найти его площадь.
б) Фронтальная работа (учитель показывает часть формулы по которой находится площадь четырехугольника, а учащиеся должны сказать что это за формула или что находится по этой формуле)
III. Инструкция по выполнению практической работы.
Учащиеся делятся на группы по 3-4 человека. В каждой группе назначается ответственный. Группе дается набор задач, которые они должны решить. Как только группа решила задачу ответственный поднимает руку учитель проверяет решение и если решение правильное, то учитель в листе учета задач, находящемся на доске ставит группе «+».
IV. Выполнение практической работы.
Вариант 1.
1. Найдите площадь фигуры
2. Сколько кафельных плиток квадратной формы со стороной 10 см потребуется для облицовки стены, имеющей форму прямоугольника со стороной 2м и 3м.
3. Найдите сторону квадрата, площадь которого равна площади прямоугольника со стороной 4м и 9м.
4. Смежные стороны параллелограмма 10 см и 12 см, острый угол 300. Найдите площадь параллелограмма.
5. В треугольнике АВС АВ=16 см, ВС =20см. Высота, проведенная к стороне АВ равна 10 см. Найдите высоту, проведенную к стороне ВС.
6. Найдите площадь трапеции с основаниями АВ и СД, если АД перпендикулярна АВ. АВ=10 см, СД=6 см, 0.
7. а) б) ?
4 5 5
12
?
8. В прямоугольнике АВСД найдите АД, если АВ=8 см, АС=10 см.
9. Является ли треугольник прямоугольным, если его стороны равны
а) 6, 8, 10 б) 5, 6, 7
Вариант 2.
1. Найдите сторону квадрата, площадь которого равна площади прямоугольника со сторонами 28 м и 7 м.
2. Пол комнаты, имеющий форму прямоугольника со сторонами 4 м и 6м нужно покрыть паркетом прямоугольной формы. Длина дощечки 30 см, ширина 5 см. сколько потребуется таких дощечек для покрытия пола?
3. Тупой угол параллелограмма равен 1500, высоты, проведенные из этой вершины равны 4 см и 6 см. Найдите площадь параллелограмма.
4. Две стороны треугольника равны 10 см и 6 см, высота, проведенная к большей стороне равна 3см. Найдите высоту, проведенную к меньшей стороне.
5. Острый угол равнобедренной трапеции равен 450, основания равны 12 см и 8 см. Найдите площадь трапеции.
6. а) А 0 б) В 0
? ?
? 6
К 1 М
В ? С
7. Боковая сторона равнобедренного треугольника равна 13 см, а основание 10 см. Найдите площадь треугольника.
8. Найдите стороны ромба, если его диагонали равны 16 см и 12 см.
9. Является ли треугольник прямоугольным, если его стороны равны
а) 15, 20, 25 б) 3, 4, 6
Лист учета решенных задач
| № группы | Ф.И | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | оценка |
| 1 | Вардугин В Синцов А Гаврилюк Д | + | + | - | + | - | + | + | + | - |
|
| 2 |
|
|
|
|
|
|
|
|
|
|
|
| 3 |
|
|
|
|
|
|
|
|
|
|
|
V.Подведение итогов урока .
Выставление оценок за урок.
VI.Задание на дом.
Стр.133 вопросы для повторения к главе VI/
Итог урока.
Спасибо! Урок окончен!
Урок - зачет
Тема урока: Урок-зачет по теме «Тела вращения»
Цели урока: формирование базовой математической подготовки.
Задачи:
образовательные: проверить качество усвоения темы «Тела вращения»;
развивающие: развитие логического мышления, памяти, навыки устного счета; способствовать умению наблюдать, анализировать, сравнивать и делать соответствующие выводы.
воспитательные: воспитание ответственного отношения к учебе, продолжить формирование познавательного интереса к предмету.
Формы организации учебно-познавательной деятельности:
Методы обучения:
наглядный
словесно-иллюстративный
практический
Оборудование:
Ход урока
I. Организационный момент.
II. Инструкция по выполнению зачета.
Зачет состоит из четырех этапов.
1 этап – проверка знания определений, теорем. 2 этап –проверка умения находить площади тел вращения. 3 этап – проверка умения ориентироваться в телах вращения. Первые три этапа каждый учащийся выполняет свое индивидуальное задание. На 4 этапе класс делится на группы. Каждая группа выбирает задачу, соответствующую их знаниям. За каждый этап выставляется оценка, затем выводится общая оценка за весь зачет.
III. Выполнение зачета.
1 этап. Проверка знания определений, теорем (каждый ученик вытягивает билет и отвечает на него)
Билет 1. Дать определение цилиндра. Назвать элементы цилиндров. Показать на модели.
Билет. Изобразить цилиндр, перечислить элементы, дать определения, показать на чертеже.
Билет 3. Что собой представляет сечения цилиндра плоскостью? Остановиться на каждом случае. Сделать чертеж.
Билет 4. Что представляет собой развертка цилиндра? По какой формуле находится полная поверхность цилиндра?
Билет 5. Дать определение конуса. Назвать виды конусов. Показать на моделях.
Билет 6. Изобразить конус, перечислить элементы, дать определения, показать на чертеже.
Билет 7. Что собой представляют сечения конуса плоскостью? Остановиться на каждом случае. Сделать чертеж.
Билет 8. Назвать формулу, связывающую высоту, радиус и образующую конуса.
Билет 9. Что представляет собой развертка конуса? Назвать формулу полной поверхности конуса.
Билет 10. Что такое усеченный конус? Формула полной поверхности усеченного конуса.
Билет 11. Дать определение шара (два определения)
Билет 12. Назвать элементы шара, показать на чертеже, дать определения.
Билет 13. Дать определение касательной прямой к шару, сформулировать ее свойство.
Билет 14. Дать определение касательной плоскости к шару. Сформулировать ее свойство.
Билет 15. Что является сечением шара плоскостью. какое сечение называется большим кругом шара?
2 этап. Проверка умения находить площади тел вращения, используя изученные формулы и производя необходимые измерения (каждый ученик получает тело вращения)
3 этап. Проверка умения ориентироваться в телах вращения (учитель задает вопрос, ученик сразу письменно на него отвечает)
Вопросы:
Тело, состоящее из всех точек пространства ,находящихся на расстоянии, небольшем данного.
Что находится по формуле Sбок + ПR2 + Пr2?
Сечение цилиндра плоскостью, параллельной оси.
Тело, образованное всеми отрезками, соединяющими данную точку с точками некоторого круга (точка не лежит в плоскости круга)
Расстояние между основаниями цилиндра.
Граница шара.
Что за формула 2ПRH
Тело, полученное при вращении прямоугольника вокруг стороны.
Сечение конуса плоскостью перпендикулярной оси конуса.
Всякое сечение шара плоскостью есть ….
Отрезок, соединяющий две точки шаровой поверхности и проходящей через цент шара
Прямая, содержащая высоту конуса.
Что за формула ПRL + ПR2
Отрезок, соединяющий вершину конуса с точкой окружности основания конуса
Плоскость, проходящая через конец радиуса, перпендикулярно радиусу.
Линия пересечения двух сфер.
Фигура, образованная при вращении равнобедренной трапеции вокруг ее оси.
Отрезок с концами, лежащими на окружностях оснований, перпендикулярно основаниям.
Что является осевым сечением конуса?
Если образующая цилиндра перпендикулярна основаниям, то цилиндр называется …
Прямая, проходящая через центр оснований цилиндра
Сечение конуса плоскостью, проходящей через две образующие.
Фигура, полученная при вращении полукруга вокруг диаметра
Перпендикуляр, опушенный из вершины конуса на плоскость основания
Сечение шара диаметральной плоскостью
Тело, полученное при вращении прямоугольного треугольника вокруг катета
4 этап. Проверка умения решать задачи по теме «Тела вращения»
Групповая работа (Учитель делит класс на группы. Учащиеся сами выбирают вариант, из которого они будут решать задачи.)
Вариант 1. (на «3»)
Радиус основания конуса 3 м, высота 4 м. Найдите образующую и полную поверхность конуса.
Вариант 2. (на «4»)
Шар пересечен плоскостью, находящейся на расстоянии 9 дм от центра шара. площадь сечения равна 16П дм2. Найдите поверхность шара.
Вариант 3. (на «5»)
Угол при вершине осевого сечения конуса с высотой 1 м равен 600. Чему равна площадь сечения, проведенного через две образующие, угол между которыми равен 450?
Лист учета знаний
| Ф.И. | 1 этап | 2 этап | 3 этап | 4 этап | Итог |
| Сулейманова Л | 5 | 4 | 4 | 4 | 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
IV. Итог урока
Итоги зачета подводятся на следующем уроке.
Литература:
Геометрия 7-9 классы. учебник для 7-9 классов, Л.С. Атанасян, М:Просвещение, 2012
Геометрия, 10-11: Учеб.для общеобразоват. учреждений /Л.С. Атанасян, В.Ф. Бутузов идр. – 12-е изд. – М.:Просвещение, 2005.
Дьяченко В.К. Организационная структура учебного процесса. М., 1989.
Зотов Ю.Б. Организация современного урока / Под ред. П.И. Пидкасистого, М., 1984.
Математика: учебник для 6 класса общеобразовательных учреждений/Г.В. Дорофеев, И.Ф. Шарыгин, С.Б. Суворова и др. Рос.акад.наук, Рос. Акад. Образования, изд-во « Просвещение». М. : Просвещение,2012
Конаржевский Ю.А. Анализ урока/ М.: Центр «Педагогический поиск», 2000
Махмутов М.И. Современный урок. 2-е изд. М., 1985.
В.А. Онищук Урок в современной школе. М.Просвещение, 1981
Педагогика. Учебное пособие для студентов и педагогических вузов и педагогических колледжей/Под ред. П.И. Пинского. – М.:Педагогическое общество России, 1998.
