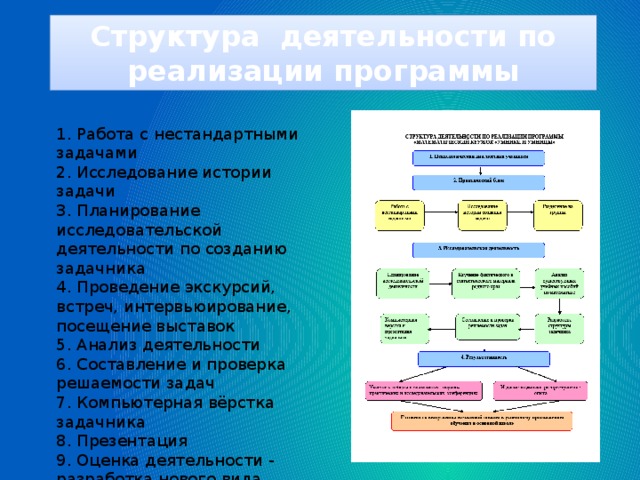
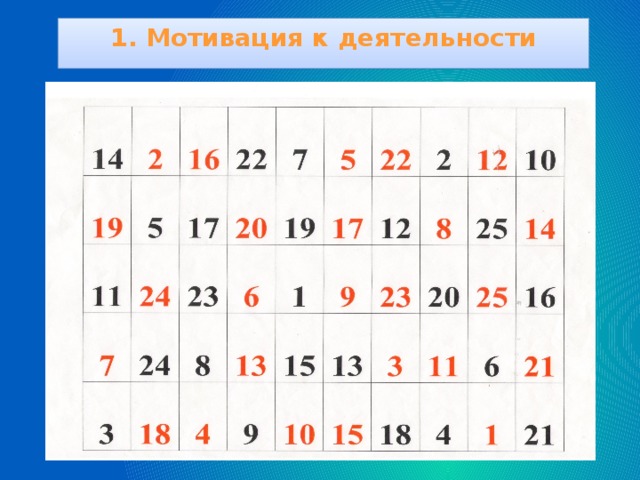
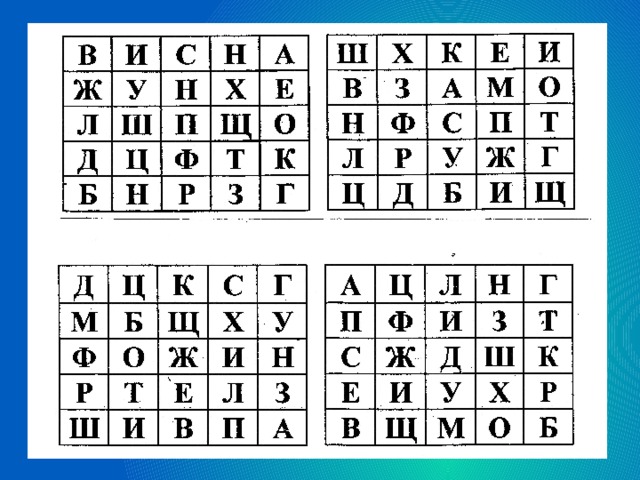
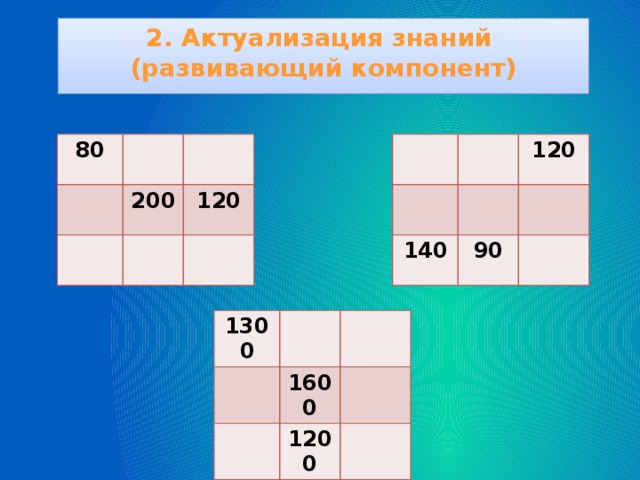
Внеурочная деятельность – это хорошая возможность для организации межличностных отношений в классе между обучающимися и классным руководителем с целью создания ученического коллектива и, конечно же, развитие интеллектуальных способностей.Занимаясь с детьми в кружке, совместно создаём задачник о нашем крае"Нягушкины задачки", договариваемся со спонсорами и типографией. Ученики с огромным интересом сами составляют задачи на основе исследований и экскурсий по родному краю.Учатся составлять и брать интервью для сбора информации. В дальнейшем каждый участник кружка является победителем олимпиад и конкурсов не только по математике, но и по другим предметам. По данной теме провела мастер-класс с учителями.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
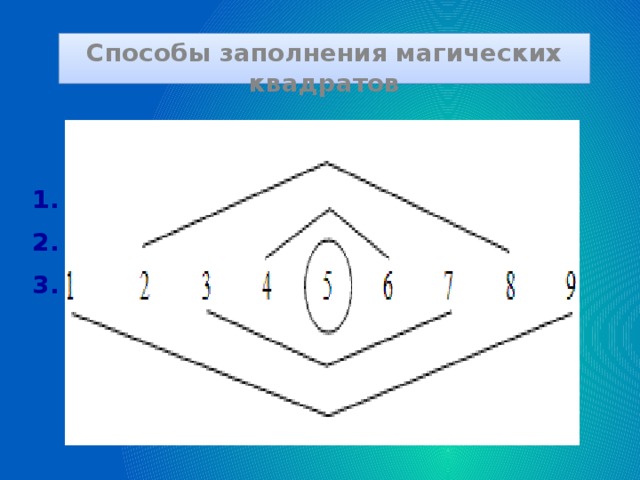
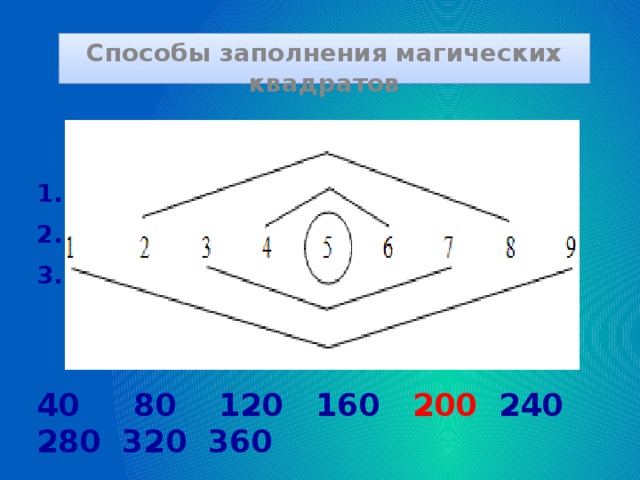
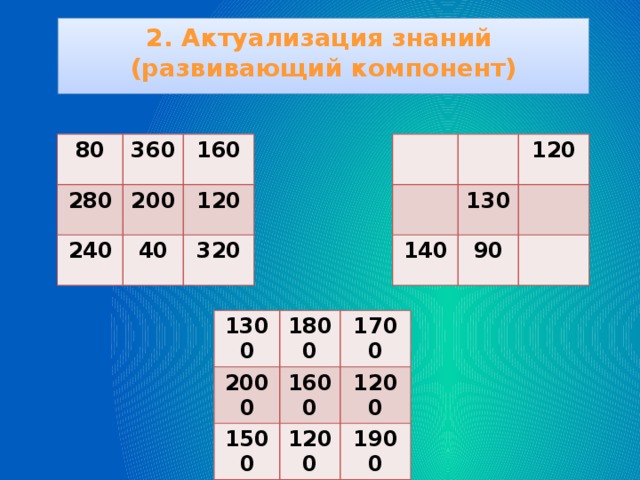
Связь УУД с внеурочной деятельностью (в рамках занятий математического кружка)
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Связь УУД с внеурочной деятельностью (в рамках занятий математического кружка) »
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
2110 руб.
3020 руб.
1230 руб.
1760 руб.
1650 руб.
2350 руб.
2110 руб.
3010 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства