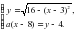Задания с параметрами традиционно считаются одними из самых сложных в школьном курсе математики.Однако в тестах по ЕГЭ и ОГЭ они обязательно присутствуют. Поэтому умение их решать- залог успеха на экзамене. Данное занятие как раз помогает школьникам научиться решатьподобные задания. Материал урока направлен на развитие логического мышления, алгоритмической культуры, интуиции, навыков исследовательской деятельности, творческих способностей ущащихся.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Занятие элективного курса: "Различные способы решения уравнений с параметром: аналитическим и графическим методом".
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Занятие элективного курса: "Различные способы решения уравнений с параметром: аналитическим и графическим методом". »
Полезное для учителя
Распродажа видеоуроков!
1900 руб.
3170 руб.
1910 руб.
3190 руб.
1720 руб.
2860 руб.
1730 руб.
2880 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
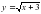 - «полу» парабола с вершиной х = -3; у= 2х – а – множество параллельных прямых, с угловым коэффициентом 2.
- «полу» парабола с вершиной х = -3; у= 2х – а – множество параллельных прямых, с угловым коэффициентом 2.

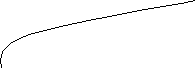

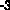


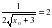
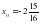 - абсцисса точки касания
- абсцисса точки касания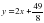 , а =
, а = 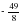


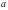 , для каждого из которых уравнение
, для каждого из которых уравнение 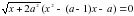 имеет только два различных корня.
имеет только два различных корня.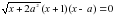

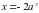 ,
, 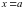 и
и 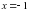 – корни исходного уравнения лишь при условии
– корни исходного уравнения лишь при условии 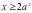 . Обратим внимание на то, что график удобнее строить на координатной плоскости
. Обратим внимание на то, что график удобнее строить на координатной плоскости 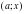 . На рисунке искомый график – объединение сплошных линий. Здесь ответ «считывается» вертикальными прямыми.
. На рисунке искомый график – объединение сплошных линий. Здесь ответ «считывается» вертикальными прямыми.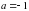 , или
, или 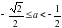 , или
, или 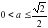 .
.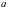 уравнение
уравнение 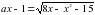 имеет единственное решение?
имеет единственное решение?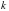 уравнение
уравнение 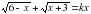 имеет решение?
имеет решение?