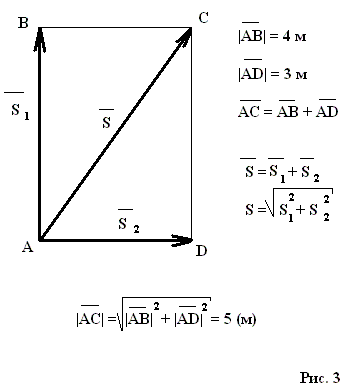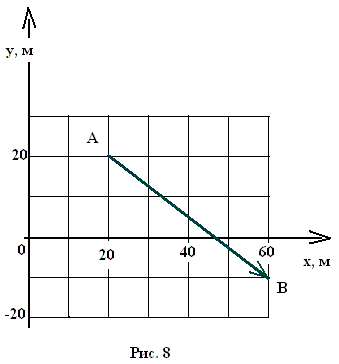« Векторы и действия над ними. Проекции вектора на координатные оси и действия над ними»

План интегрированного урока по геометрии и физике

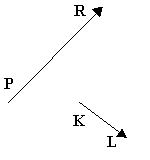
Тема « Векторы и действия над ними. Проекции вектора на координатные оси и действия над ними»

Цель урока: формирование навыков применения понятия вектора для решения геометрических и физических задач.

Задачи: повторить и обобщить знания учащихся о векторе, проекции вектора на координатные оси, научить применять полученные знания для решения физических и геометрических задач;

формировать функциональную грамотность на уроке;

развивать информационно-технологическую и коммуникативную компетенцию, прививать навыки самостоятельного решения задач, учить делать выводы и умозаключения;

воспитывать культуру математической и физической речи, умение выслушивать других при работе в классе, организованность и дисциплинированность.

Оборудование: компьютер, проектор.

Тип урока: урок комплексного применения знаний.

Метод обучения: словесно-объяснительный-иллюстративный.

Используемые новые технологии: уровневая дифференциация, метод проектов

Используемые формы работы: индивидуальная работа.

Ход урока:

I.Организационный момент:

а) психологический настрой учащихся на урок;

б) постановка целей и задач урока;

в)сообщение плана урока.

При изучении физики и математики часто прослеживаются межпредметные связи, связь с жизнью, решаются прикладные задачи. Физика как наука о явлениях природы опирается на строгий математический аппарат, без которого невозможно выразить ни одну закономерность. Великий А. Эйнштейн сказал: ”Что касается математики, то она интересует меня лишь постольку, поскольку я могу применить ее в физике”. И это применение безгранично. Так тема « Векторы и действия над ними целиком повторяется в физике, а тема « Проекции вектора на координатные оси» применяется и в геометрии.Поэтому сегодня мы и проводим интегрированный урок по геометрии и физике, чтобы показать полное совпадение тем и взаимосвязь понятий через применение знаний полученных на геометрии при решении физических задач.

II.Актуализация знаний учащихся: /фронтальная устная работа/

1.Что называется вектором в пространстве? Его обозначения.

2.Что называется длиной вектора? Ее обозначение.

3.Какие векторы называются коллинеарными?

4.Какие векторы называются сонаправленными? Обозначение.

5.Какие векторы называются противоположно направленными? Обозначение.

6.Какие векторы называются равными? Обозначение.

7.Какой может быть величина?

8.Чем отличаются векторные величины от скалярных? Приведите примеры.

III. Повторение и обобщение материала: индивидуальный опрос

IV. Проверка знаний учащихся:

Практическая работа по теме «Сложение и вычитание векторов»

1. Постройте вектор, равный сумме векторов MK и KL. Запишите результат в виде равенства.

2. Пользуясь «правилом треугольника», постройте вектор, равный сумме векторов AB и CD. Запишите результат в виде равенства.

3. Постройте вектор, равный разности векторов TQ и TS. Запишите результат в виде равенства.

4. Пользуясь «правилом треугольника», постройте вектор, равный разности векторов MN и FE. Запишите результат в виде равенства.

5. Пользуясь «правилом параллелограмма», постройте вектор, равный сумме векторов PR и KL Запишите результат в виде равенства.

а) работа с учебником:учебник, рис 11,стр 11

б) работа с презентацией:

Вопрос: Если известны координаты начального положения тела и вектор перемещения, как можно найти координаты, определяющие его конечное положение?

Ответ рассмотрим на примере движения тела на плоскости.. Пусть 9В класс из точки с координатами М₀ (x₀ y₀) совершил перемещение S= М₀ М в точку М с координатами (х, у).

Вопрос. Как получить проекцию вектора перемещения на оси Х и У?

Опустив перпендикуляры на оси Х и У получили проекции вектора перемещения Sх и Sу.

Из рисунка видно, что

Х=Х₀ + S_х У = У₀ + S_у

S_х = Х- Х₀ S_{у =}У- У₀

Длина вектора перемещения S= S₁+S₂

Рассмотрим применение данных формул при решении следующей задачи: Известна шутка “Как правильнее сказать: три да четыре суть пять или три да четыре есть пять?”

Три да четыре не всегда дает в сумме 7, ответ может быть и 5, если три и четыре представляют собой векторные величины. Векторные величины складываются геометрически, скалярные – арифметически. Пример “рис. 2

Вопрос. Какое правило применяется для нахождения вектора перемещения.? ( Сложение по правилу параллелограмма).

VI.Закрепление.

Решите задачу самостоятельно.

На рисункепоказана траектория движения материальной точки из A в B. Найдите координаты точки в начале и конце движения, перемещение, проекции перемещения на оси координат

Ответы:A (20 м; 20 м); B (60 м; – 10 м); S= 50 м; S_х= 40 м; S_у = – 30 м.

– 30 м.

7Рефлексия: -что нового вы узнали на уроке;

-что интересного было на уроке;

- что вы не усвоили на уроке?

9.Подведение итогов, выставление оценок

10.Домашнее задание.а) по геометрии §1,2 повторить, № 64,67

б) по физике § 3 , упр. 2