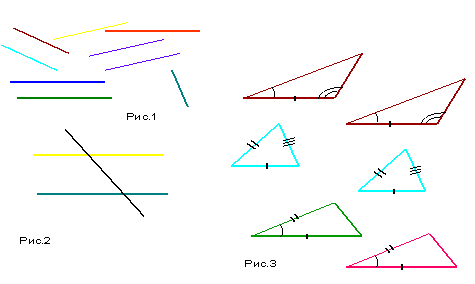Планирование урока для __8_______ класса _геометрия________(предмет)
Дата _18.10.2013__________________
№ урока __13_______________________
Тема урока_Теорема Фалеса. Пропорциональные отрезки_________________________________
____________________________________________________________________________________
Цель:__Сформировать знания о теореме Фалеса__________________________________________
_____________________________________________________________________________________
Задачи:_Образовательные: сформировать навыки построения простейших чертежей,________
измерительных навыков; сформировать и развить умения и навыки решения геометрических _
задач на вычисление, на доказательство и на построение;____________________________________
Развивающие: умственное развитие умений обосновывать и доказывать утверждения,___________
развитие логического мышления учащихся; математической интуиции и ___________________
потенциальных творческих способностей каждого учащегося; _______________________________
Воспитательные: воспитание культуры общения, уважения к истории, приобщение к________ _ценностям, накопленным математической наукой в ходе __________________________________
ее развития;__________________________________________________________________________
Тип урока:_изучение и первичное закрепление новых знаний______________________________
Методы обучения_Объяснительно – иллюстративный___________________________________
Структура урока
- Организационный момент
2. Мотивация урока.
Дорогие ребята!
Я надеюсь, что этот урок пройдет интересно, с большой пользой для всех. Очень хочу, чтобы те, кто еще равнодушен к царице всех наук, с нашего урока ушел с глубоким убеждением, что геометрия – интересный и нужный предмет.
Французский писатель XIX столетия Анатоль Франс однажды заметил: “Учиться можно только весело… Чтобы переваривать знания, надо поглощать их с аппетитом”.
Давайте последуем совету писателя на сегодняшнем уроке: будьте активны, внимательны, поглощайте с большим желанием знания, которые пригодятся вам в дальнейшей жизни.
^ 3. Актуализация опорных знаний.
Фронтальный опрос учащихся:
1. Какие отрезки называются равными?
2. Какие прямые называются параллельными? На рис. 1 покажите параллельные прямые.
3. Какие углы называются вертикальными, внутренними накрест лежащими? Покажите их на рис.2
4. Сформулируйте теорему о свойстве параллельных прямых, пересечённых третьей прямой.
5. Сформулируйте признаки равенства треугольников. По каким признакам равны треугольники на рис 3?
4. Изучение нового материала.
Историческая справка.
К 6 веку до нашей эры главным городом греческого государства был Милет.
В это время в Греции был расцвет науки и культуры. Почти все философы Древней Греции тщательно занимались математикой, в частности, геометрией.
Фалес – купец, политический деятель, астроном, математик, живший в Милете, первый доказал ряд геометрических теорем. Эти положения были частично известны еще вавилонянам и египтянам, но в отличие от вавилонской и египетской геометрии, имевшей преимущественно практический характер, греческая геометрия характеризуется стремлением установить, что геометрические факты справедливы в любом случае.
К сожалению, до нас не дошли работы Фалеса и другие первоисточники, относящиеся к раннему периоду развития греческой математики, когда создавались первые математические доказательства. Мы можем судить о том времени только по отдельным отрывкам, сохранившимся в более поздних сочинениях.
Как философ, Фалес учил, что явления мира не случайны, мир не хаотичен, а закономерен. Он считал, что вода есть начало всего. Из нее возникло все существующее и в нее, в конце концов, опять превращается.
Фалес сделал ряд открытий в области астрономии: установил время равноденствий и солнцестояний, определил продолжительность года, впервые наблюдал Малую медведицу. Особую славу ему принесло предсказание солнечного затмения, происшедшего в 585 г. до н. э. Вот почему он был причислен к группе “семи мудрецов древности”.
Фалес также входил в число знаменитых семи мудрецов, чьи изречения дошли до наших дней. Ему приписывают следующие:
- Старше всех вещей – Бог, ибо он не рожден.
- Прекраснее всего – космос, ибо он – творение Бога.
- Больше всего – пространство, ибо оно вмещает всех.
- Мудрее всего - время, ибо оно обнаруживает всё.
- Быстрее всего – мысль, ибо она бежит без остановки.
- Сильнее всего – необходимость, ибо она одолевает всех.
Теорема Фалеса гласит, если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.
Докажем теорему Фалеса: если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
Решение:
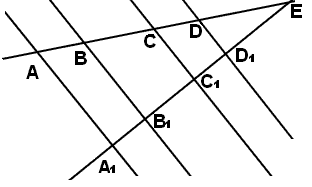
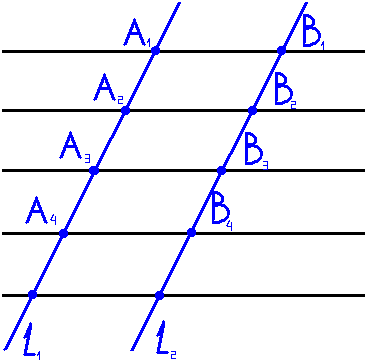
Пусть на прямой l1 отложены равные отрезки А1А2, А2А3, А3А4, … и через их концы проведены параллельные прямые, которые пересекают прямую l2 в точках В1, В2, В3, В4, …(рис. 1). Требуется доказать, что отрезки В1В2, В2В3, В3В4, … равны друг другу. Докажем, например, что В1В2 = В2В3.
Рассмотрим сначала случай, когда прямые l1 и l2 параллельны (рис. 1, а). Тогда А1А2 =В1В2 и А2А3= В2В3 как противоположные стороны параллелограммов А1В1В2А2 и А2В2В3А3. Так как А1А2=А2А3, то и В1В2=В2В3. Если прямые l1 и l2 не параллельны, то через точку В1 проведем прямую l, параллельную прямой l1(рис. 1, б). Она пересечет прямые А2В2 и А3В3 в некоторых точках C и D. Так как А1А2 = А2А3, то по доказанному В1С=CD. Отсюда получаем В1В2=В2В3. Аналогично можно доказать, что В2В3=В3В4 и т. д.
Рис.1. а) б)
5. Закрепление нового материала.
Решение задач по№60,61,64(1).
Задача.
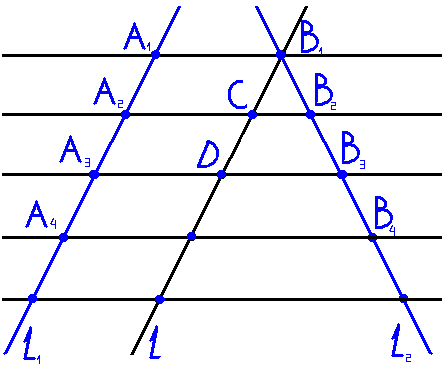
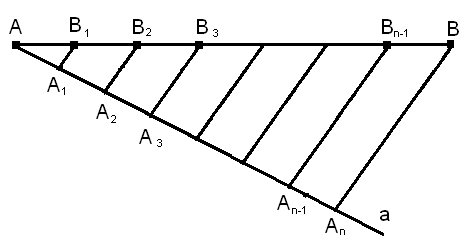
Разделите данный отрезок АВ на n равных частей.
Решение. Проведем из точки А полупрямую а, не лежащую на прямой АВ (рис.3). Отложим на полупрямой а равные отрезки: АА1,А1А2, А2А3, …, Аn-1An. Соединим точки Аn и В. Проведем через точки А1, А2, …,Аn-1 прямые, параллельные прямой АnВ. Они пересекают отрезок АВ в точках В1,В2, …,Вn-1, которые делят отрезок АВ на n равных отрезков (по теореме Фалеса).
6. Физминутка для глаз.
-Не поворачивая головы, обведите взглядом стену класса по периметру по часовой стрелке, классную доску по периметру против часовой стрелки, треугольник, изображенный на стенде по часовой стрелке и равный ему треугольник против часовой стрелки. Поверните голову налево и посмотрите на линию горизонта, а теперь на кончик своего носа. Закройте глаза, сосчитайте до 5, откройте глаза и …
7. Самостоятельная работа учащихся.
Решить № 64(2).
8.Итоги урока. Рефлексия.
Что больше всего тебе запомнилось на уроке?
Что удивило?
Что понравились больше всего?
Каким ты хочешь увидеть следующий урок?
Домашнее задание: выучить п.4, вопросы 1-2 с.20, решить №30
(творческое): подготовить сообщение «Занимательные странички из жизни Фалеса».