| Организационный момент (1 мин) | Приветствие, проверка подготовленности к учебному занятию, организация внимания детей. | Включаются в ритм урока.
Слушают учителя. | Личностные УУД готовность к выполнению норм и требований учителя |
| Мотивация и целеполагание (5 мин) | - Ребята, сегодня мы проверим как же вы усвоили пройденный материал по теме «Квадратные уравнения». Профессор Цифиркин прислал нам письмо, давайте прочтем его. Ученикам 8 класса школы № N От профессора Цифиркина Заявление 15.01 сего года у меня из кабинета исчезла ценная математическая фигура. Прошу принять меры для розыска этой фигуры. С уважением профессор Цифиркин P.S. Преступник оставил «след», который я прошу передать той из команд, которая лучше подготовится к розыску. Ребята, чтобы помочь профессору, вам нужно разделиться на две команды следователей и пройти конкурс на лучшую подготовку к следствию. По итогам этих конкурсов лучшая команда получает «след», на котором написано условие задачи. Решив это задание, команда найдет пропавшую фигуру.
| Слушают условия конкурса и зачитанное письмо. Готовятся выполнять задания | Регулятивные УУД Планировать цель деятельности |
| Повторение пройденного материала (28 мин) | Задания командам Проверка быстроты реакции: а) х2-49=0; а) х2-4х=0 в) 9х2=25 в) 4х2=81
2. Умение вести перекрестный допрос. Один ученик из каждой команды выбирается в качестве свидетеля. Команда противников задает ему вопрос по теме: «Квадратные уравнения». Проверка логического мышления; При каком с (b) уравнение имеет единственный корень: 6x2-4x+с=0 , х2+bх+36=0?
Умение проводить экспертизу: Установить, являются ли числа 4+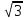 и 4- и 4-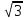 Корнями уравнения х2-8х+13=0, Способом подстановки. (с помощью теоремы Виета) Победившая команда получает «след» с задачей. Задача.: В уравнении х2+рх-140=0 один из корней равен – 28. Число р укажет номер кабинета, а второй корень – стол, где находится указанная фигура. | Решают предложенные задания, объясняют свои ответы х2-49=0; х2-4х=0; х2=49; х(х-4)=0; х=7; х=-7. х=0; х=4 9х2=25; 4х2=81; х2=25/9; х2=81/4; х=5/3; х=9/2; х=-5/3. х=-9/2.
6x2-4x+с=0 Чтобы уравнение имело единственный корень, дискриминант должен быть равен 0. Тогда получаем: D=(-4)2-4*6*с=16-24с 16-24с=0; 24с=16; с=2/3. х2+bх+36=0 Чтобы уравнение имело единственный корень, дискриминант должен быть равен 0. Тогда получаем: D=b2-4*36=b2-144 b2-144=0; b2=144; b=12; b=-12. х2-8х+13=0 теорема Виета: (4+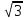 )+ (4- )+ (4-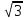 )=8=-b )=8=-b (4+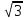 )* (4- )* (4-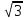 )=16-3=13=c )=16-3=13=c Вывод: данные числа являются корнями этого уравнения. Способ подстановки: (4+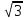 )2 -8*(4+ )2 -8*(4+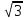 )+13=16+8 )+13=16+8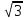 +3-32-8* +3-32-8*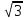 +13=32-32=0 – верно +13=32-32=0 – верно (4-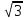 )2 -8*(4- )2 -8*(4-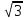 )+13=16-8 )+13=16-8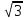 +3-32+8* +3-32+8*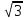 +13=32-32=0 – верно +13=32-32=0 – верно Вывод: данные числа являются корнями этого уравнения.
х2+рх-140=0 х1=-28. По теореме, обратной теореме Виета найдем второй корень: х2=-140/(-28)=5 Тогда р=-(-28+5)=-(-23)=23 Ответ: р=23, х2=5.
| Регулятивные УУД Выделение из системы знаний ранее изученного Коммуникативные УУД Владеть устной и письменной математической речью, аргументировано отстаивать свою точку зрения Познавательные УУД
Предметные УУД Применение и знание:
|
| Рефлексия (3 мин) | Итак, сегодня мы с вами решали задачи профессора Цифиркина. Это были уравнения. Давайте вспомним еще раз типы и способы решения таких уравнений. | Отвечают на вопросы учителя | Коммуникативные УУД Владеть устной и письменной математической речью, аргументировано отстаивать свою точку зрения Познавательные УУД Строить логичные рассуждения и делать выводы. |