Технологическая карта урока «Заключение в скобки» 6 класс

Деятельность учителя

Деятельность уч-ся

УУД

1.Организационный этап

Приветствие, подготовка класса к работе, организация внимания детей.

добрый день, добрый час!

как я рада видеть вас!

друг на друга посмотрели

и тихонечко все сели.

Нашу работу на уроке мне хотелось бы начать с не большого тренинга:

Думать будем,
Решать будем,
Друг другу во всём
помогать будем!

Приветствуют учителя, друг друга.

Настраиваются на рабочий лад

Личностные: самоопределяются, настраиваются на урок

Познавательные: ставят перед собой цель: «Что я хочу получить сегодня от урока»

Коммуникативные: планируют учебное сотрудничество с учителем и одноклассниками

2. Актуализация знаний

Вступительное слово учителя.

Повторение пройденного на прошлом уроке.

Ознакомление с рабочей картой урока.

Проверка правил. Игра «Ромашка»

- На доске висит ромашка. На каждом лепестке написано задание. Ваша задача выйти к доске, вытянуть лепесток, прочитать вслух задание и ответить на него.

Устный счет.

- Ребята, я вам буду показывать карточки с примерами, ваша задача в уме сосчитать, поднять руку и сказать ответ.

Участвуют в работе по повторению, в беседе с учителем, отвечают на поставленный вопросы.

1) Сформулируйте правило о сложении двух чисел с разными знаками. Приведите пример.

2) Сформулируйте правило о сложении двух чисел с одинаковыми знаками. Приведите пример.

3) Чему равна сумма одинаковых чисел с противоположными знаками? Приведите пример.

4) Каким законом мы пользуемся при внесении и вынесении общего множителя за скобки? Приведите пример и запишите его на доске.

5) Сформулируйте правило раскрытия скобок, перед которыми стоит знак «+».

6) Сформулируйте правило раскрытия скобок, перед которыми стоит знак «-».

1) 15 – (- 58) = 4) 28 – 100 = 7) -7*(-6) =

2) – 36 – 24 = 5) – 20 + 6 = 8) – 15:3 =

3) -70 + 16= 6) – 75 + 75 = 9) -4*5 =

Познавательные: анализируя и сравнивая предлагаемые задания, извлекают необходимую информацию для построения математического высказывания

Регулятивные: выполняют тренировочное учебное действие

Коммуникативные: выражают свои мысли с достаточной полнотой и точностью, используют чужие высказывания для обоснования своего суждения

3. Постановка цели и задач урока. Мотивация учебной деятельности учащихся.

Задания на раскрытие скобок.

Ребята, давайте, с вами выполним раскрытие скобок в следующем примере:

5·(13+7)=5·13+ 5·7

Если посмотреть на это равенство слево на право, то мы выполнили какое действие?

А если посмотреть, наоборот, с права на лево?

Поэтому тема нашего урока.

Поставим цели на урок

Рассмотрим с вами еще пример:

-6+7-3+10

Рассмотрим решение примеров (один пример вместе другой самостоятельно):

Теперь осталось вывести правило на основе всех наших действий.

Достигли ли мы с вами первую цель нашего урока?

Ребята, давайте сравним его с правилом раскрытия скобок. Похожи ли они?

Устно по заданиям слайдов.

- Раскрытие скобок

- Мы в скобки заключали.

- «Заключение в скобки»

- Изучить правило заключения в скобки перед которыми стоит знак «+» или «-».

- Применить это правило при решении заданий.

Да.

Комментируют ответы.

Личностные: самоопределение.

Регулятивные: целеполагание.

Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками.

Познавательные: умения формулировать вопросы к тексту, самостоятельно формулировать ответы с опорой на текст.

4. Первичное усвоение новых знаний

Следующий этап работы нашего урока я предлагаю продолжить вот под таким девизом:

Я тетрадочку открою

И с наклоном положу,

Я от вас, друзья, не скрою,

Ручку я вот так держу.

Сяду прямо, не нагнусь,

За работу я возьмусь.

Решение примеров по цепочке из учебника

№ 375

Заключите первые два слагаемых в скобки, перед скобками поставьте знак «+»:

№ 376

Заключите первые два слагаемых в скобки, перед скобками поставьте знак «-»:

По цепочке по одному ученику к доске, остальные работают в тетрадях

№ 375

Заключите первые два слагаемых в скобки, перед скобками поставьте знак «+»:

а) 79 – 48 + 15 – 8 = + (79 – 48) + 15 – 8

б) – 56 + 38 – 12 + 100 = + ( -56 + 38) -12 + 100

в) 43 + 59 – 35 – 11 = + (43 + 59) – 35 -11

г) – 43 – 59 + 35 + 11 = + ( -43 – 59) + 35 + 11

д) 42 – 79 + 13 – 1 = + (42 – 79) + 13 – 1

е) – 57 + 48 – 17 + 23 = + ( -57 + 48) – 17 + 23

№ 376

Заключите первые два слагаемых в скобки, перед скобками поставьте знак «-»:

а) 79 – 48 + 15 – 8 = - (-79 + 48) + 18 – 8

б) – 56 + 38 – 12 + 100 = -(56 – 38) – 12 + 100

в) 43 + 59 – 35 – 11 = - (-43 – 59) – 35 – 11

г) – 43 – 59 + 35 + 11 = -(43 + 59) + 35 + 11

д) 42 – 79 + 13 – 1 = - (-42 + 79) + 13 – 1

е) -57 + 48 – 17 + 23 = - (57 – 48) – 17 + 23

Познавательные УУД: формирование умений по использованию математических знаний для решения различных математических задач и оценки полученных результатов;

–  по использованию доказательной математической речи;

–  по работе с информацией, в том числе и с различными математическими текстами;

– регулятивные УУД (формирование умений ставить личные цели деятельности, планировать свою работу, действовать по плану, оценивать полученные результаты;

– коммуникативные УУД формирование умений совместно с другими детьми в группе находить решение задачи и оценивать полученные результаты.

Учитель проводит физминутку.

Проговаривая, учащиеся выполняют упражнения для снятия усталости

5. Первичное закрепление

Организует работу в группе.

Приложение 1.

1.Найдите ошибку:

- Незнайке дали домашнее задание, которое он выполнил с ошибкой. Ход его решения оказался неверным. Решив пример заново, найдите те ошибки, которые допустил Незнайка в домашней работе. (Ошибка подчеркнута линией.)

Организует работу в парах.

2. Решить уравнения.

Приложение 2.

Под руководством учителя разбиваются на группы, а затем на пары.

Выполняют задания, помогая друг другу, корректируя ответы и вычисления.

Познавательные: выделяют необходимую информацию, планируют свою деятельность, прогнозируют результат

Регулятивные: в ситуации затруднения регулируют свою деятельность

Коммуникативные: планируют сотрудничество с одноклассниками и учителем

6. Первичная проверка понимания

Предлагает учащимся выполнить тест на применение правил раскрытия и заключения в скобки.

Приложение 3

Организует проведение самостоятельной работы.

Критерии оценивания работы:

«5»- нет ошибок, «4»-4 задания правильно, «3»- 3 задания правильно, «2» - менее 3 заданий правильно.

Организует взаимопроверку по ответам со слайда.

Выполняют задания теста с решением в тетрадях и отмечают ответы в тетрадях.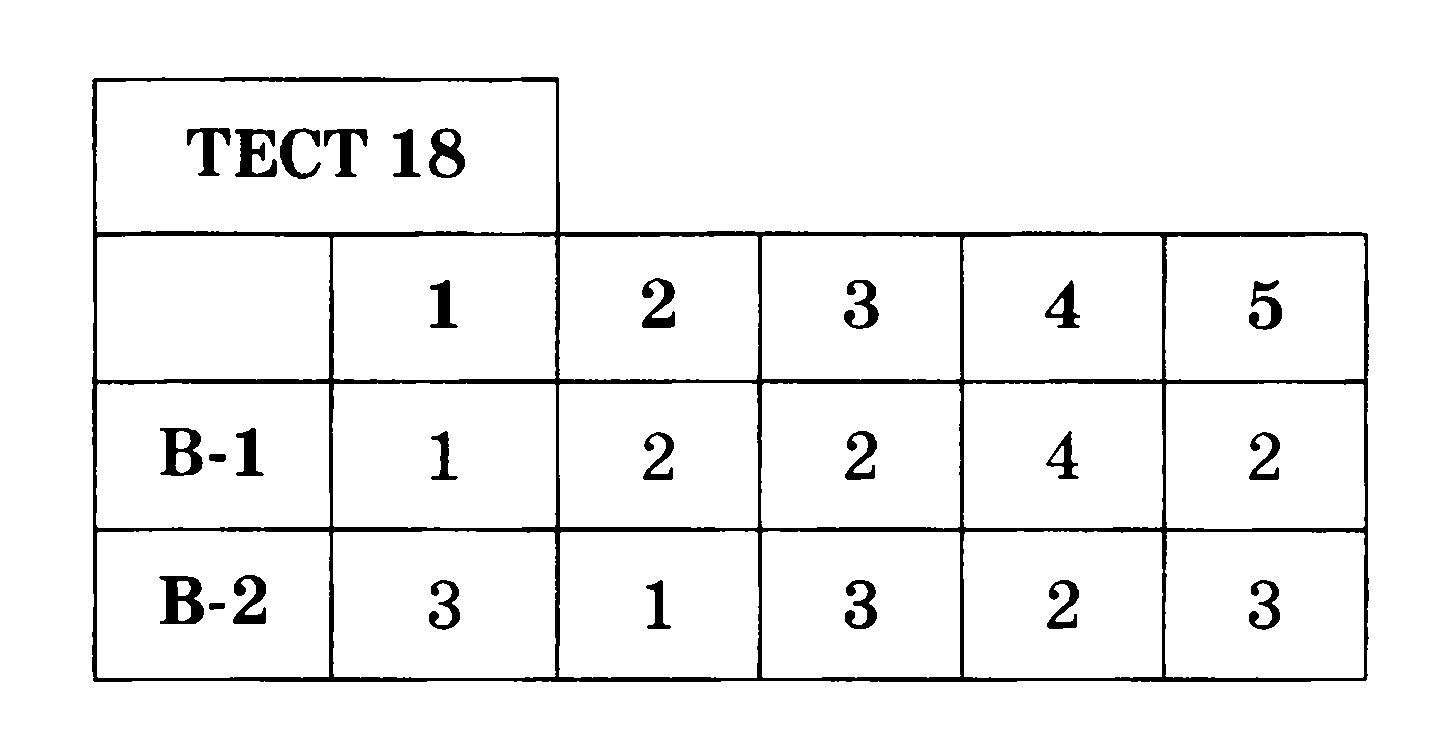

Личностные: стараются следовать в поведении моральным нормам

Познавательные: самостоятельно выполняют действия по алгоритму

Регулятивные: проявляют познавательную инициативу, контролирую свои действия

Коммуникативные: осознают применяемый алгоритм с достаточной полнотой

7. Информация о домашнем задании, инструктаж о его выполнении

Информирует о домашнем задании.

Стр. учить правило.

Карточки (приложение 5)

Воспринимают информацию, записывают в дневники домашнее задание

Регулятивные:

Умение структурировать знания;

оценка процесса и результатов деятельности.

8. Рефлексия ( подведение итогов занятия)

Предлагает подвести итоги урока.

Организует фронтальную беседу по вопросам:

· Сегодня на уроке я научился…

·     Мне было интересно…

·     Мне было трудно:

·     Я понял …

·     Я почувствовал, что…

·     Больше всего мне понравилось…

·     Мне было интересно…

·     Своей работой на уроке я доволен (не совсем, не доволен), потому что…

В заключении учитель обобщает ответы учащихся, оценивает работу на уроке и делает вывод о достижении цели урока всем классом.

Продолжают фразы предложенные учителем по выбору.

Объективно оценивают свое пребывание на уроке.

Регулятивные: Уметь оценивать правильность выполнения действия на уровне адекватной ретроспективной оценки.

Личностные: Способность к самооценке на основе критерия успешности учебной деятельности.

Этап урока

Критерии оценивания

Баллы

Ромашка

«5» ответил верно правило без ошибок и помощи учителя

«4» ответил верно, но были не большие не точности.

«3» ответил с помощью учителя.

«2» не ответил правило

Устный счет (примеры)

«5» ответил верно

«4» ответил верно, но были не большие не точности.

«3» ответил, но определил не верно знак ответа или не правильно посчитал.

«2» не правильно ответил или вообще не ответил

Устный счет (раскрытие скобок)

«5» ответил верно

«4» ответил верно, но были не большие не точности.

«3» ответил, но определил не верно знак ответа или не правильно посчитал.

«2» не правильно ответил или вообще не ответил

Решение примеров на заключение в скобки

«5» верно выполнил пример на доске

«4» пример выполнил верно но были не большие не точности

«3» пример выполнен, но определен не верно знак ответа или не правильно посчитано.

«2» не решил пример

Работа в группе

«5» активно работал в работе группы (пары), давал верные ответы

«4» принимал участие в работе группы (пары), но данные тобой решения были не совсем верны

«3» принимал участие в работе группы (пары), но решения данные тобой были не верны

«2» не принимал участие в работе группы (пары), пример не решал.

Работа в парах

Самостоятельная работа

«5»- нет ошибок

«4»-4 задания правильно

«3»- 3 задания правильно

«2» - менее 3 заданий правильно.

Посчитайте общее количество баллов за все этапы урока и поставьте оценку за работу на уроке.

«5» - 32 - 35 балла

«4» - 25– 31 баллов

«3» - 18 – 24баллов;

«2» - 17 и менее

Итоговая оценка:

К-1

Упростите выражение, раскрыв скобки, и выполните там, где возможно, действия.

5– (3 + x)

– x + (x + 2,7)

Решите уравнение:

14 – (x – 2) = 23

К-2. Упростите выражение, раскрыв скобки, и выполните там, где возможно, действия.

5– (3 + x)

– x + (x + 2,7)

– 2 + (3,1 – x)

Решите уравнение:

14 – (x – 2) = 23

(38 + x) – 18 = 31

К-3.Упростите выражение, раскрыв скобки, и выполните там, где возможно, действия.

5– (3 + x)

– x + (x + 2,7)

– 2 + (3,1 – x)

Решите уравнение:

14 – (x – 2) = 23

(38 + x) – 18 = 31

12 – (x – 3) = 3

К-1

Упростите выражение, раскрыв скобки, и выполните там, где возможно, действия.

5– (3 + x)

– x + (x + 2,7)

Решите уравнение:

14 – (x – 2) = 23

К-2. Упростите выражение, раскрыв скобки, и выполните там, где возможно, действия.

5– (3 + x)

– x + (x + 2,7)

– 2 + (3,1 – x)

Решите уравнение:

14 – (x – 2) = 23

(38 + x) – 18 = 31

К-3.Упростите выражение, раскрыв скобки, и выполните там, где возможно, действия.

5– (3 + x)

– x + (x + 2,7)

– 2 + (3,1 – x)

Решите уравнение:

14 – (x – 2) = 23

(38 + x) – 18 = 31

12 – (x – 3) = 3

К-1

Упростите выражение, раскрыв скобки, и выполните там, где возможно, действия.

5– (3 + x)

– x + (x + 2,7)

Решите уравнение:

14 – (x – 2) = 23

К-2. Упростите выражение, раскрыв скобки, и выполните там, где возможно, действия.

5– (3 + x)

– x + (x + 2,7)

– 2 + (3,1 – x)

Решите уравнение:

14 – (x – 2) = 23

(38 + x) – 18 = 31

К-3.Упростите выражение, раскрыв скобки, и выполните там, где возможно, действия.

5– (3 + x)

– x + (x + 2,7)

– 2 + (3,1 – x)

Решите уравнение:

14 – (x – 2) = 23

(38 + x) – 18 = 31

12 – (x – 3) = 3

К-1

Упростите выражение, раскрыв скобки, и выполните там, где возможно, действия.

5– (3 + x)

– x + (x + 2,7)

Решите уравнение:

14 – (x – 2) = 23

К-2. Упростите выражение, раскрыв скобки, и выполните там, где возможно, действия.

5– (3 + x)

– x + (x + 2,7)

– 2 + (3,1 – x)

Решите уравнение:

14 – (x – 2) = 23

(38 + x) – 18 = 31

К-3.Упростите выражение, раскрыв скобки, и выполните там, где возможно, действия.

5– (3 + x)

– x + (x + 2,7)

– 2 + (3,1 – x)

Решите уравнение:

14 – (x – 2) = 23

(38 + x) – 18 = 31

12 – (x – 3) = 3