Тема урока: "Сложение и вычитание дробей с разными знаменателями"
Класс: 6 класс
Тип урока: повторение пройденного материала.
Форма организации учебной деятельности: фронтальная, групповая, индивидуальная.
Технология: технология учебно-игровой деятельности, информационно-коммуникационная технология.
Цель: повторить правило сложения и вычитания дробей с разными знаменателями и закрепить в решении примеров, уравнений и задач.
Задачи урока:
Образовательные:
Развивающие:
развивать активную познавательную деятельность обучающихся, интерес к математике,
развивать умения преодолевать трудности при решении математических задач
формировать умения чётко и ясно излагать свои мысли;
Воспитательные:
прививать учащимся навык самостоятельности в работе, учить трудолюбию, аккуратности;
воспитывать умение работать с имеющейся информацией в необычной ситуации;
воспитывать уважение к математике, умение видеть математические задачи в окружающем нас мире.
Оборудование и наглядность:
компьютер, проектор, экран;
презентация PowerPoint .
раздаточный материал (индивидуальные карточки с дифференцированными заданиями)
Ход урока
1.Организационный момент
2.Актуализация знаний
Постановка цели урока
Продолжаем работать над сравнением, сложением и вычитанием дробей с разными знаменателями. Цель нашего урока попробуем сформулировать вместе (повторить правило, отработать умения и навыки на сравнение, сложение и вычитание дробей с разными знаменателями).
Есть такая поговорка «попал в тупик», т. е. попал в положение из которого трудно найти выход, а у немцев аналогичная поговорка гласит, «попал в дроби», ( т. к. действия над дробями в средние века считались самой сложной областью математики.)
Я надеюсь, ребята, что на нашем уроке не будет трудных положений, из которых мы не сможем найти выход. А поможет нам навигатор.
Навигатор - это путеводная нить, помогающая выйти из затруднительного положения; путь, ведущий к цели в сложных условиях.
Сегодня мы отправимся в путешествие, а навигатором будут ваши знания по теме: «Сложение и вычитание дробей с разными знаменателями». Именно они, ваши знания помогут вам в затруднительном положении.
Итак, запишите в тетради число, классная работа, тема урока
Пункт Домашнее проверочное
Проверка домашнего задания
Проверим. как вы знаете теоретический материал и умение применять его в упражнениях.
Работа в группах.
Каждая группа получает карточки с теоретическими вопросами:
-Как сравнить, сложить, вычесть две дроби с разными знаменателями?
-Как привести дроби к одному знаменателю?
-Что значит сократить дробь?
- Как сравнить дроби с одинаковым знаменателем?
- Как сравнить дроби с одинаковым числителем?
Вычислите:
1-я № 327(е), 2-я № 327 (д), 3-я № 327 (в)
В это время по 1 обучающемуся решают задания у доски:
1) Записать дроби в порядке возрастания: 2/3, 1/4, 5/6, 1/2 (отв: 1/4, 1/2 , 2/3, 5/6)
2) Вычислите: 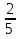 +
+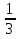 ;
; 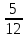 -
- 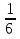 ;
; 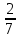 +
+ 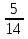 . (отв: 11/15, 3/12=1/4, 9/14)
. (отв: 11/15, 3/12=1/4, 9/14)
Проверка заданий на доске.
Пункт Задумчивый
Решение задач из учебника ( 8-10 мин):
3 б - № 338 (отв: 14/8=7/4м),
3 б - № 339 (отв: 33/100 т),
2 б - № 337 (отв: 10/20=1/2 км)
Самопроверка ( на доске ответы)
Пункт Отдых
(физкультминутка)
Пункт Внимательный
Работа в группах.
Найдите ошибки в решенных уравнениях и решите верно:
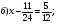
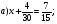
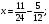
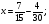
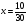
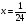 ( отв: а) х = 10/30 б) х = 21/24)
( отв: а) х = 10/30 б) х = 21/24)
Пункт Вычислительный
Решите примеры (самостоятельно):
Найдите сумму дробей 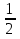 и
и 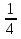 . ( 3/4)
. ( 3/4)
Найдите разность дробей 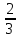 и
и 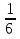 . ( 3/6)
. ( 3/6)
Найдите сумму чисел: 1) 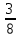 и
и 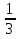 ; (17/24)
; (17/24)
Найдите разность чисел: 1) 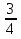 и
и 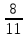 ; ( 1/44)
; ( 1/44)
Вычислите значение выражения: 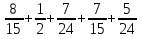 . ( 2)
. ( 2)
1/44 – б; 3/4 – д; 2 – и; 17/24 – о; 3/6 – р.
и прочитайте закодированный термин ("Дроби")
Пункт Итоговый
Домашнее задание: П11, 10 ( алгоритмы),
индивидуальные карточки с дифференцированными заданиями: задания А 1-4 всем, + В 1-2, С1 (поименно) и любой желающий.
Оцените свою работу в течение урока: за каждый "+" - 1 балл.
Рефлексия:
Оцените степень сложности урока:
Вам было на уроке:
Легко; Обычно; Трудно.
Оцените степень Вашего усвоения материала:
Усвоил полностью, могу применять;
Усвоил полностью, но затрудняюсь применять;
Усвоил частично;
Не усвоил, нужна консультация.