| 2 курс
| лекционный материал |
Лекция №3
Тема: Параллельность прямых, прямой и плоскости
План:
Параллельные прямые в пространстве
Параллельность трёх прямых
Параллельность прямой и плоскости
Параллельные прямые в пространстве
Введем понятие параллельных прямых в пространстве.
Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Параллельность прямых  и
и  обозначается так:
обозначается так: 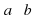 . На рисунке прямые
. На рисунке прямые  и
и  параллельны, а прямые
параллельны, а прямые  и
и 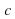 ,
,  и
и 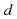 не параллельны.
не параллельны.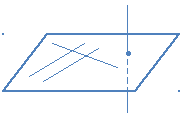
Докажем теорему о параллельных прямых.
Теорема. Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.
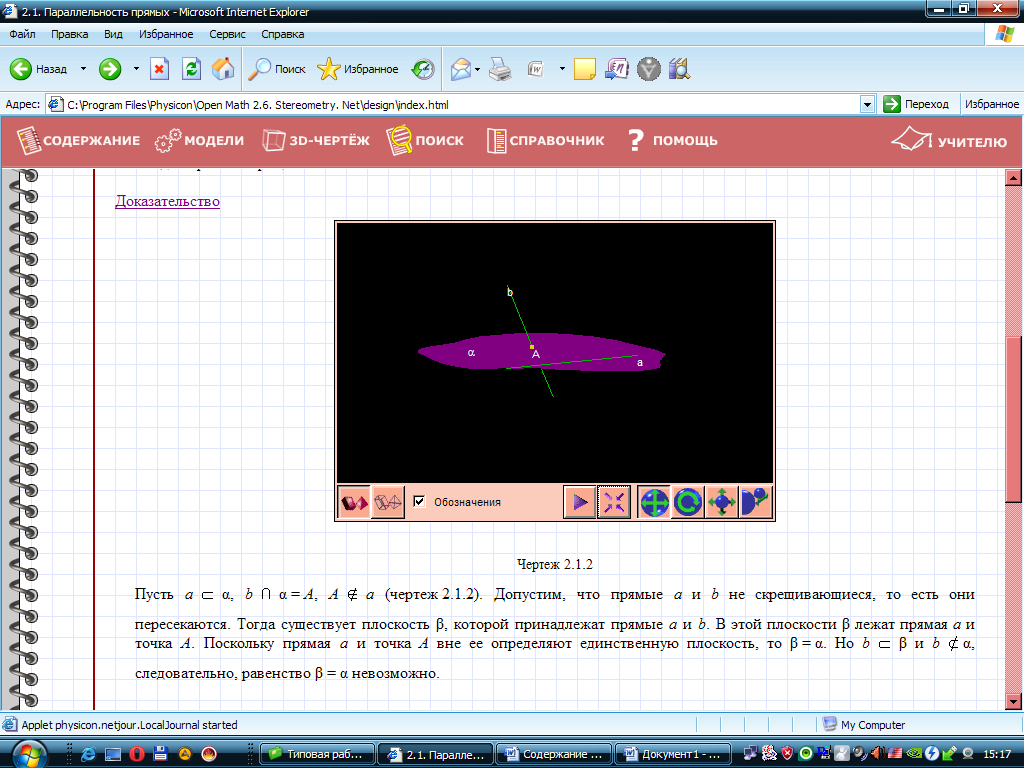
Доказательство. Рассмотрим прямую  и точку
и точку 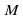 , не лежащую на этой прямой (смотреть рисунок).
, не лежащую на этой прямой (смотреть рисунок). 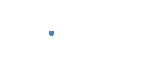
Через прямую  и точку
и точку 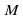 проходит плоскость, и притом только одна. Обозначим эту плоскость буквой
проходит плоскость, и притом только одна. Обозначим эту плоскость буквой  . Прямая, проходящая через точку
. Прямая, проходящая через точку 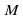 параллельно прямой
параллельно прямой  , должна лежать в одной плоскости с точкой
, должна лежать в одной плоскости с точкой 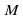 и прямой
и прямой  , то есть должна лежать в плоскости
, то есть должна лежать в плоскости  . Но в плоскости
. Но в плоскости  , как известно из курса планиметрии, через точку
, как известно из курса планиметрии, через точку 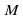 проходит прямая, параллельная прямой
проходит прямая, параллельная прямой  , и притом только одна. На рисунке эта прямая обозначена буквой
, и притом только одна. На рисунке эта прямая обозначена буквой  . Итак,
. Итак,  – единственная прямая, проходящая через точку
– единственная прямая, проходящая через точку 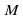 параллельно прямой
параллельно прямой  . Теорема доказана.
. Теорема доказана.
В дальнейшем нам понадобятся также понятия параллельных отрезков, параллельных отрезка и прямой, параллельных лучей. Два отрезка называются параллельными, если они лежат на параллельных прямых. Аналогично определяется параллельность отрезка и прямой, а также параллельность двух лучей. На рисунке отрезки 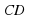 и
и 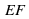 параллельны
параллельны 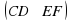 , а отрезки
, а отрезки 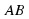 и
и 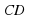 не параллельны, отрезок
не параллельны, отрезок 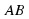 параллелен прямой
параллелен прямой 
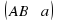 .
.
Параллельность трёх прямых
Докажем лемму о пересечении плоскости параллельными прямыми, необходимую для дальнейшего изложения.
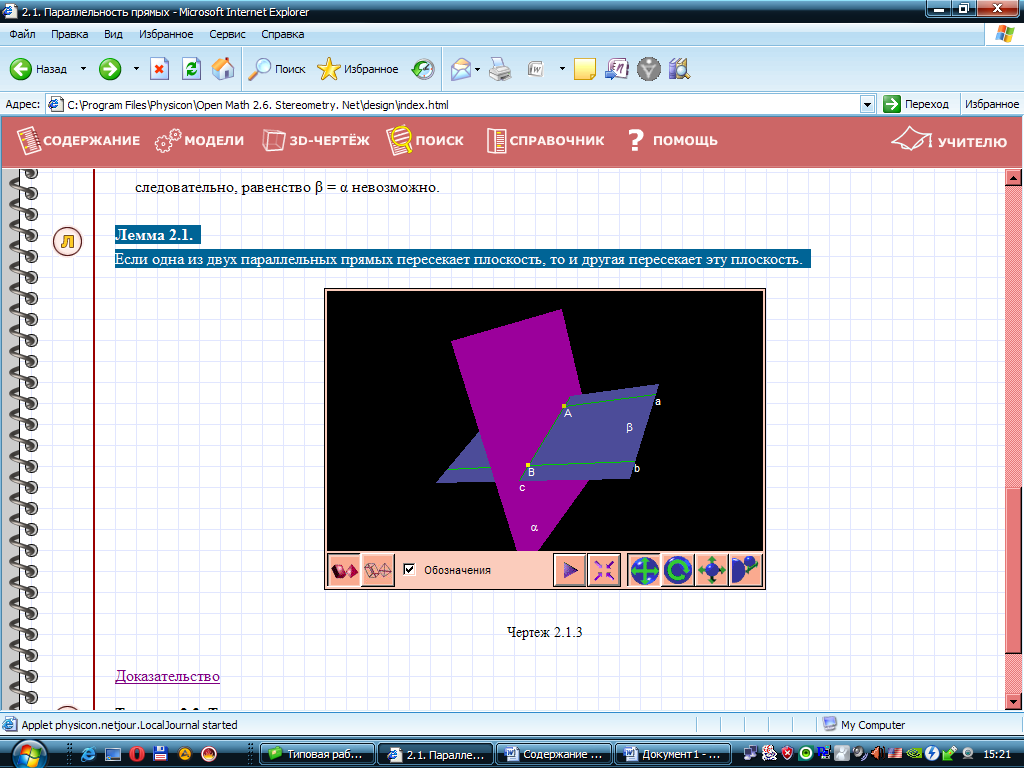
Лемма. Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.
Доказательство. Рассмотрим параллельные прямые  и
и  , одна из которых – прямая
, одна из которых – прямая  – пересекает плоскость
– пересекает плоскость  в точке
в точке 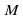 (смотреть рисунок).
(смотреть рисунок). 
Докажем, что прямая  также пересекает плоскость
также пересекает плоскость  , то есть имеет с ней только одну общую точку.
, то есть имеет с ней только одну общую точку.
Обозначим буквой  плоскость, в которой лежат параллельные прямые
плоскость, в которой лежат параллельные прямые  и
и  . Так как две различные плоскости
. Так как две различные плоскости  и
и  имеют общую точку
имеют общую точку 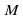 , то по аксиоме 3 они пересекаются по некоторой прямой
, то по аксиоме 3 они пересекаются по некоторой прямой  (смотреть рисунок ниже). Эта прямая лежит в плоскости
(смотреть рисунок ниже). Эта прямая лежит в плоскости  и пересекает прямую
и пересекает прямую  (в точке
(в точке 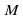 ), поэтому она пересекает параллельную ей прямую
), поэтому она пересекает параллельную ей прямую  в некоторой точке
в некоторой точке  . Прямая
. Прямая  лежит также в плоскости
лежит также в плоскости  , поэтому
, поэтому  – точка плоскости
– точка плоскости  . Следовательно,
. Следовательно,  – общая точка прямой
– общая точка прямой  и плоскости
и плоскости  .
.

Докажем теперь, что прямая  не имеет других общих точек с плоскостью
не имеет других общих точек с плоскостью  , кроме точки
, кроме точки  . Это и будет означать, что прямая
. Это и будет означать, что прямая  пересекает плоскость
пересекает плоскость  . Действительно, если бы прямая
. Действительно, если бы прямая  имела еще одну точку с плоскостью
имела еще одну точку с плоскостью  , то она целиком лежала бы в плоскости
, то она целиком лежала бы в плоскости  и, значит, была бы общей прямой плоскостей
и, значит, была бы общей прямой плоскостей  и
и  , то есть совпадала бы с прямой
, то есть совпадала бы с прямой  . Но это невозможно, так как по условию
. Но это невозможно, так как по условию 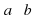 , а прямые
, а прямые  и
и  пересекаются. Лемма доказана.
пересекаются. Лемма доказана.
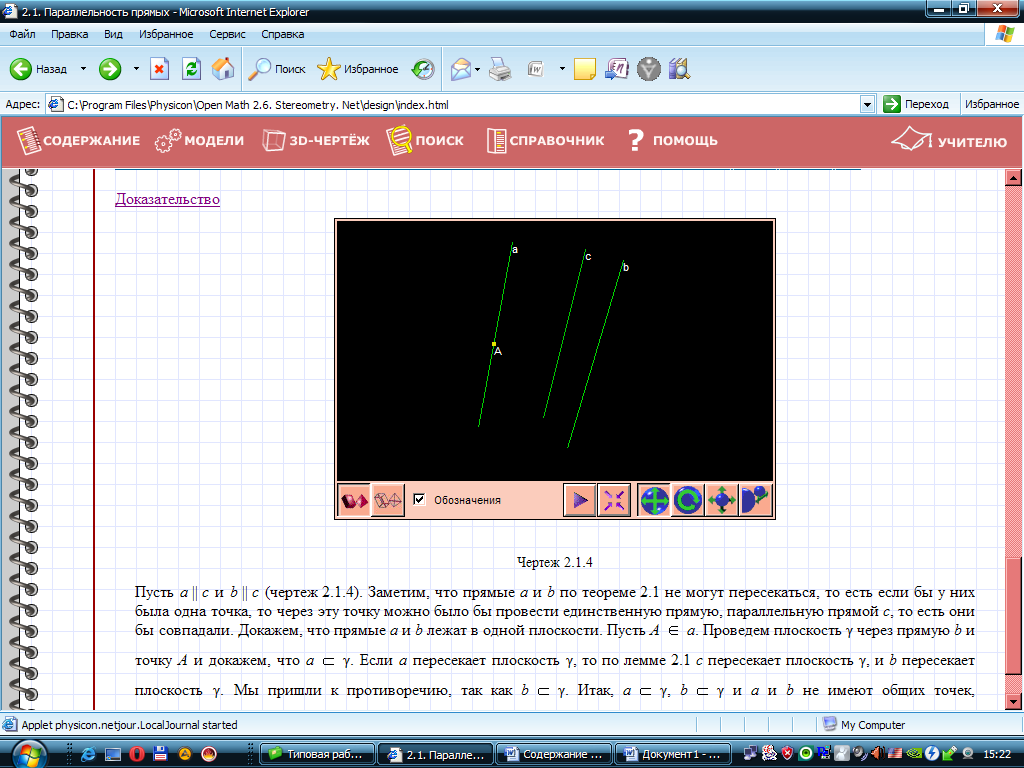
Из курса планиметрии известно, что если три прямые лежат в одной плоскости и две из них параллельны третьей прямой, то эти две прямые параллельны. Докажем аналогичное утверждение для трех прямых в пространстве.
Теорема. Если две прямые параллельны третьей прямой, то они параллельны.
Доказательство. Пусть  и
и  . Докажем, что
. Докажем, что 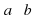 . Для этого нужно доказать, что прямые
. Для этого нужно доказать, что прямые  и
и  : 1) лежат в одной плоскости и 2) не пересекаются.
: 1) лежат в одной плоскости и 2) не пересекаются.
1. Отметим какую-нибудь точку  на прямой
на прямой  и обозначим буквой
и обозначим буквой  плоскость, проходящую через прямую
плоскость, проходящую через прямую  и точку
и точку  (смотреть рисунок).
(смотреть рисунок). 
Докажем, что прямая  лежит в этой плоскости. Действительно, если допустить, что прямая
лежит в этой плоскости. Действительно, если допустить, что прямая  пересекает плоскость
пересекает плоскость  , то по лемме о пересечении плоскости параллельными прямыми прямая
, то по лемме о пересечении плоскости параллельными прямыми прямая 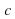 также пересекает плоскость
также пересекает плоскость  . Но так как
. Но так как  , то и прямая
, то и прямая  пересекает плоскость
пересекает плоскость  , что невозможно, ибо прямая
, что невозможно, ибо прямая  лежит в плоскости
лежит в плоскости  .
.
2. Прямые  и
и  не пересекаются, так как в противном случае через точку их пересечения проходили бы две прямые (
не пересекаются, так как в противном случае через точку их пересечения проходили бы две прямые ( и
и  ), параллельные прямой
), параллельные прямой 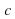 , что невозможно. Теорема доказана.
, что невозможно. Теорема доказана.
Параллельность прямой и плоскости
Если две точки прямой лежат в данной плоскости, то по аксиоме 2 вся прямая лежит в этой плоскости. Отсюда следует, что возможны три случая взаимного расположения прямой и плоскости в пространстве:
а) прямая лежит в плоскости;
б) прямая и плоскость имеют только одну общую точку, то есть пересекаются;
в) прямая и плоскость не имеют ни одной общей точки.
Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек.
Параллельность прямой  и плоскости
и плоскости  обозначается так:
обозначается так:  . Наглядное представление о прямой, параллельной плоскости, дают натянутые троллейбусные или трамвайные провода – они параллельны плоскости земли. Другой пример дает линия пересечения стены и потолка – эта линия параллельна плоскости пола.
. Наглядное представление о прямой, параллельной плоскости, дают натянутые троллейбусные или трамвайные провода – они параллельны плоскости земли. Другой пример дает линия пересечения стены и потолка – эта линия параллельна плоскости пола.
Заметим, что в плоскости пола имеется прямая, параллельная этой линии. Такой прямой является, например, линия пересечения пола с той же самой стеной. На рисунке указанные прямые обозначены буквами  и
и  . Оказывается, что если в плоскости
. Оказывается, что если в плоскости  имеется прямая
имеется прямая  , параллельная прямой
, параллельная прямой  , не лежащей в плоскости
, не лежащей в плоскости  , то прямая
, то прямая  и плоскость
и плоскость  параллельны (смотреть рисунок ниже). Другими словами, наличие в плоскости
параллельны (смотреть рисунок ниже). Другими словами, наличие в плоскости  прямой
прямой  , параллельной прямой
, параллельной прямой  , является признаком, по которому можно сделать вывод о параллельности прямой
, является признаком, по которому можно сделать вывод о параллельности прямой  и плоскости
и плоскости  . Сформулируем это утверждение в виде теоремы.
. Сформулируем это утверждение в виде теоремы.
Теорема. Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.
Доказательство. Рассмотрим плоскость  и две параллельные прямые
и две параллельные прямые  и
и  , расположенные так, что прямая
, расположенные так, что прямая  лежит в плоскости
лежит в плоскости  , а прямая
, а прямая  не лежит в этой плоскости. Докажем, что
не лежит в этой плоскости. Докажем, что  . Допустим, что это не так. Тогда прямая
. Допустим, что это не так. Тогда прямая  пересекает плоскость
пересекает плоскость  , а значит, по лемме о пересечении плоскости параллельными прямыми прямая
, а значит, по лемме о пересечении плоскости параллельными прямыми прямая  также пересекает плоскость
также пересекает плоскость  . Но это невозможно, так как прямая
. Но это невозможно, так как прямая  лежит в плоскости
лежит в плоскости  . Итак, прямая
. Итак, прямая  не пересекает плоскость
не пересекает плоскость  , поэтому она параллельна этой плоскости. Теорема доказана.
, поэтому она параллельна этой плоскости. Теорема доказана.
Докажем еще два утверждения, которые часто используются при решении задач.
 . Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
. Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
Пусть через данную прямую  , параллельную плоскости
, параллельную плоскости  , проходит плоскость
, проходит плоскость  , пересекающая плоскость
, пересекающая плоскость  по прямой
по прямой  .
. 
Докажем, что  . Действительно, эти прямые лежат в одной плоскости (в плоскости
. Действительно, эти прямые лежат в одной плоскости (в плоскости  ) и не пересекаются: ведь в противном случае прямая
) и не пересекаются: ведь в противном случае прямая  пересекала бы плоскость
пересекала бы плоскость  , что невозможно, поскольку по условию
, что невозможно, поскольку по условию  .
.
 . Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости.
. Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости.
В самом деле, пусть  и
и  – параллельные прямые, причем прямая
– параллельные прямые, причем прямая  параллельна плоскости
параллельна плоскости  . Тогда прямая
. Тогда прямая  не пересекает плоскость
не пересекает плоскость  , и, следовательно, по лемме о пересечении плоскости параллельными прямыми прямая
, и, следовательно, по лемме о пересечении плоскости параллельными прямыми прямая  также не пересекает плоскость
также не пересекает плоскость  . Поэтому прямая
. Поэтому прямая  либо параллельна плоскости
либо параллельна плоскости  , либо лежит в этой плоскости.
, либо лежит в этой плоскости.
Вопросы на закрепление темы
Какие две прямые в пространстве называются параллельными?
Сформулируйте и докажите теорему о параллельных прямых.
Сформулируйте лемму о пересечении плоскости параллельными прямыми.
Если две прямые параллельны третьей прямой, то они …? Докажите.
Прямая и плоскость называются параллельными, если …?
Сформулируйте и докажите теорему о параллельности прямой и плоскости.
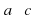 и
и  , то
, то 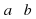 .
. 
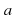 ,
, 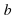 и точка
и точка 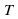 . Провести через точку
. Провести через точку 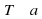 . Выберем на прямой
. Выберем на прямой 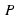 и проведем искомую прямую
и проведем искомую прямую 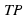 .
. 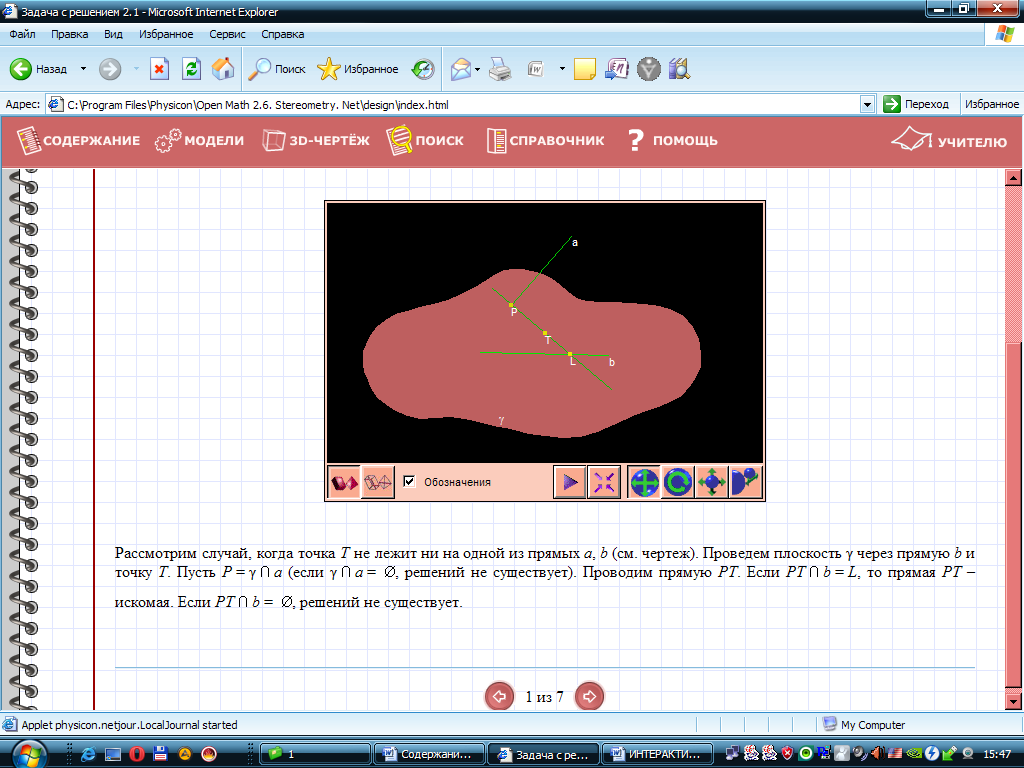
 через прямую
через прямую 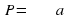 (если
(если 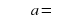 , решений не существует). Проводим прямую
, решений не существует). Проводим прямую 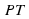 . Если
. Если 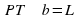 , то прямая
, то прямая 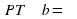 , решений не существует.
, решений не существует.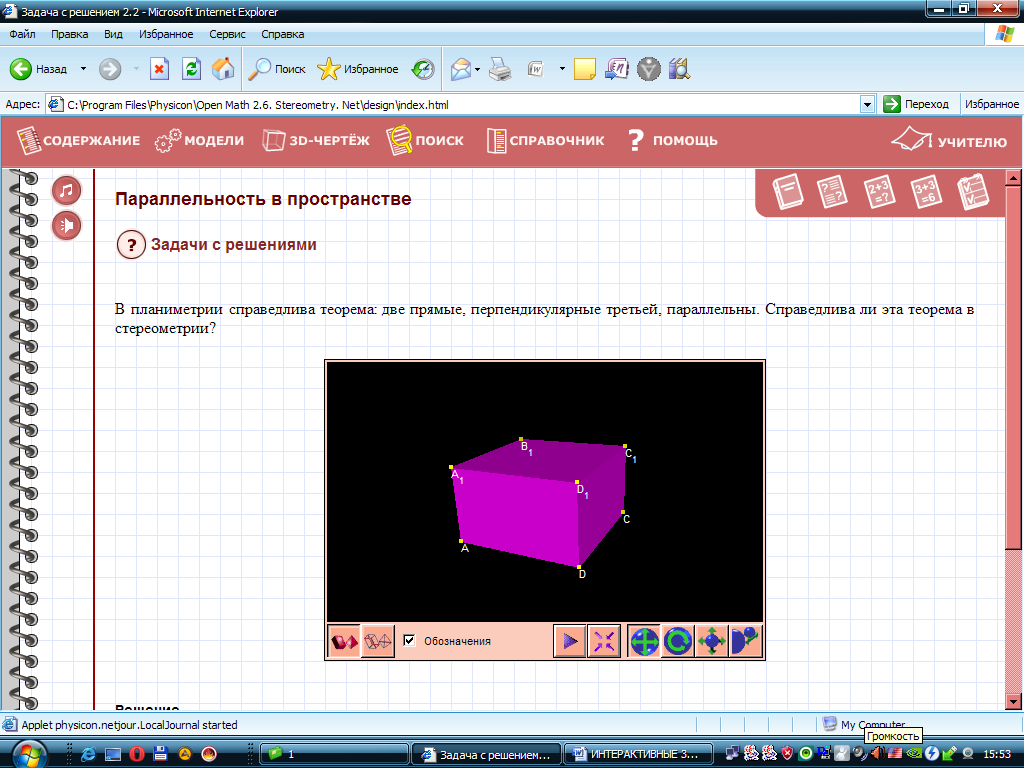
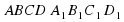 .
. 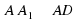 и
и 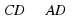 , но прямые
, но прямые 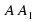 и
и 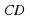 не параллельны (это скрещивающиеся прямые).
не параллельны (это скрещивающиеся прямые). 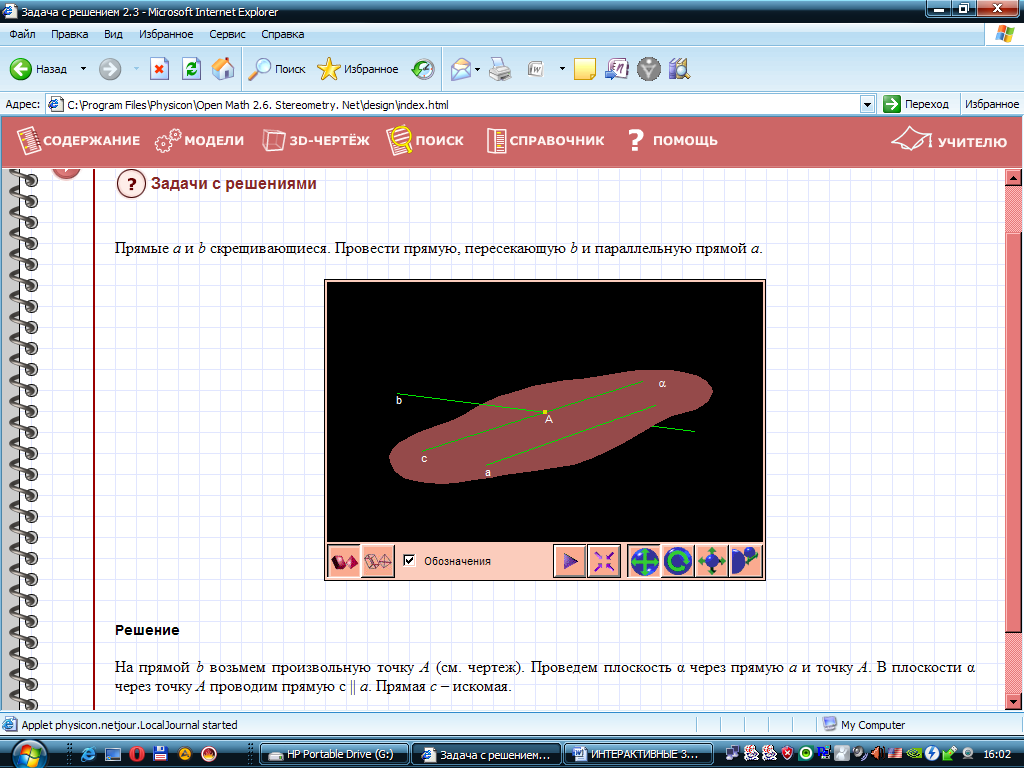
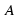 . Проведем плоскость
. Проведем плоскость  через прямую
через прямую 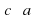 . Прямая
. Прямая  и
и  обозначается так:
обозначается так: 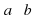 . На рисунке прямые
. На рисунке прямые 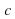 ,
, 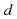 не параллельны.
не параллельны.
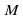 , не лежащую на этой прямой (смотреть рисунок).
, не лежащую на этой прямой (смотреть рисунок). 
 . Прямая, проходящая через точку
. Прямая, проходящая через точку 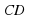 и
и 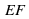 параллельны
параллельны 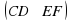 , а отрезки
, а отрезки 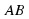 и
и 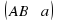 .
.

 плоскость, в которой лежат параллельные прямые
плоскость, в которой лежат параллельные прямые 















