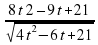11 класс, алгебра
Математический профиль
Тема урока. Применение производной в различных областях науки и техники
Пояснительная записка
Данный урок является завершающим по теме «Дифференциальное исчисление». Урок разработан для учащихся 11 математического класса.
Очень часто ученики при изучении той или иной темы задают вопрос, зачем это нужно, как это может пригодиться в жизни. Поэтому в своей практике я хотя бы несколько уроков провожу таким образом, чтобы ребята увидели не только абстрактные вычисления, но и практическое применение.
Только 45 мин длится урок, а учителю необходимо сделать очень много: провести опрос, проверить домашнее задание, разобрать новый материал, закрепить его. Поэтому для создания рабочей атмосферы считаю целесообразным на каждом уроке использовать интерактивные и компьютеризированные методы обучения, которые не только экономят время, но и привлекают учащихся к активному восприятию материала.
Проведение уроков с использованием интерактивных и информационных технологий, на основе межпредметных связей – это мощный стимул в обучении. Посредством таких уроков активизируются психические и интеллектуальные процессы учащихся, стимулируется развитие познавательного интереса. Из этого следует актуальность данной разработки урока на тему «Применение производной в различных областях науки и техники», так как для его сопровождения с помощью программы PowerPoint создана динамическая презентация.
Так как по учебному плану изучение темы «Производная. Применение производной» заканчивается во ІІ семестре, то ключевой нитью проходит через тему и данный урок в частности подготовка учащихся к ЕГЭ.
Форма проведения: творческая лаборатория
Тип урока: урок формирования компетентности в прикладном
использовании знаний, умений и навыков по теме
«Производная функции»
Цель урока:
формировать представления об общих математических методах в разных отраслях наук, умения комплексного применения знаний на основе межпредметных связей;
развивать умение анализировать и систематизировать имеющуюся информацию; содействовать развитию мыслительных операций: анализ, синтез, обобщение; формированию умений самооценки и взаимооценки; обрабатывать информацию;
развивать умения оценивать свои способности, свое положение в группе, контактировать с товарищами; содействовать формированию творческой деятельности учащихся, уверенности в своих знаниях; воспитывать интерес к предмету через содержание учебного материала.
Оборудование:
компьютер, мультимедийный проектор;
презентация к уроку;
справочные материалы с основными формулами и правилами дифференцирования;
карточки-задания для индивидуальной работы;
тесты;
карточки для групповой работы.
Форми работы на уроке:
фронтальная, индивидуальная, групповая
Оформление:
Высказывания известных ученых по теме урока
Рано или поздно всякая математическая идея находит применение в том или ином деле (А.Н.Крылов)
Нет ни одной области в математике, которая когда-либо не окажется применимой к явлениям действительного мира (Н.И.Лобачевский)
Слеп физик без математики (М.В.Ломоносов)
Технологическая карта урока
![]()
| № | Этап урока | Методический прием | Форма работы | Задача | Деятельность учителя
| Деятельность учащихся | Время
|
| 1 | Организационный момент. Мотивация. Постановка целей урока | «Удиви!» | Фронтальная | Создать рабочую атмосферу, положительный микроклимат в классе, настроить учащихся на работу | После проверки готовности класса к уроку сообщает тему, цели и план проведения урока | Записывают тему урока. | 2` |
| 2 | Актуализация опорных знаний, умений, навыков учащихся | Самопроверка домашнего задания | Индивидуальная | Провести коррекцию типичных ошибок учащихся при решении стандартных задач по теме | Дает консультации по мере необходимости | Выполняют самопроверку | 3` |
| Экспресс-опрос | Фронтальная работа | проверить знания учащихся по данной теме проверить сформированность грамотной математической речи | Задает вопросы по проверке теоретической подготовки к уроку | Отвечают с мест | 5` |
| Страничка абитуриента | Индивидуальная письменная | повторить и закрепить навыки вычисления производной
| Поясняет задание, следит за самостоятельностью выполнения | Работают самостоятельно с тестами | 5` |
| 3 | Операционно-познавательная часть: Решение проблемных задач | Решение задач разными способами |
Парная | Закрепить навыки применения производной. к решению задач
| Координатор действий Комментирует работу учащихся | Учащиеся выступают, слушают, задают вопросы Демонстрируют результаты своей деятельности | 13` |
| Индивидуальные разноуровневые задания |
Индивидуальная
|
| Проблемная задача | Фронтальная |
| 4 | Практическая часть: Решение исследовательских задач | Интерактивная технология (работа в группах) | Групповая | содействовать формированию активной творческой деятельности, развивать мотивацию учащихся, сформировать умение комплексного применения знаний, умений, навыков и их перенос в новые условия | Разбивает класс на группы, распределяет задания, ставит задачи перед каждой группой. Управляет работой групп. Заслушиваются итоги каждой группы | Решают задачи на применение производной при решении прикладных задач | 15` |
| 5 | Подведение итогов. Рефлексия | Открытый микрофон | Фронтальная | определить уровень достижения целей урока и меру участия каждого учащегося в занятии, оценка работы школьников.
| Подводит итоги всех этапов урока, просит высказать свое мнение об уроке. | Формулируют итоги урока, дают оценку своих знаний. | 3` |
| 7 | Инструктаж по домашнему заданию | Задание на выбор | Фронтальная | Дать установку на качественное выполнение домашнего задания, создать атмосферу успеха | Дает пояснение по домашнему заданию | Записывают домашнее задание | 2` |
Ход урока
Организационный момент.
Мотивация. Постановка целей урока
Здравствуйте.
Сегодня мы подводим итог большой работе, которую мы с вами проделали, изучая важную тему математического анализа «Теория дифференциального исчисления» (слайд 1)
Урок проведем в форме лаборатории дифференциальных исчислений, целью работы которой является формирования компетентности в прикладном использовании знаний, умений и навыков по теме «Производная функции»
Тема работы коллектива сотрудников лаборатории «Применение производной в различных областях науки и техники».
(Откройте тетради. Запишите число, классная работа, тему урока.)
Эпиграфом к работе хочу взять слова Лобачевского (слайд 2):
«…нет ни одной области в математике, которая когда-либо не окажется применимой к явлениям действительного мира…»
И эти слова мы сегодня попытаемся подтвердить на уроке.
Производная относится к числу математических понятий, которые носят межпредметный характер, и широко применяются в физике, химии, биологии, в технике и других отраслях наук. Изучение материала по теме урока имеет принципиально важное значение, так как здесь показывается приложение производной к решению различных физических и технических задач, то есть возможности применения элементов дифференциального исчисления в описании и изучении процессов и явлений реального мира (слайд 3).
План работы лаборатории дифференциальных исчислений 11-А класса (слайд 4):
Рабочее совещание
Решение прикладных, проблемных задач
Творческий поиск (самостоятельное исследование)
Подведение итогов работы
Задание на следующий день исследований
Актуализация опорных знаний, навыков, умений учащихся
(рабочее совещание)
Самоанализ выполнения домашнего задания
Перед тем, как начать работу, проверим, насколько вы погрузились дома в эту тему. Откройте домашнее задание. На доске записаны фрагменты решения и шкала оценивания. Проверьте и самостоятельно оцените свою подготовку к уроку.
Есть ли вопросы по домашнему заданию?
Методический прием: экспресс-опрос
Повторим основные теоретические сведения, которые помогут нам в дальнейшей работе (слайд 5, 6)
Сформулируйте определение производной функции в данной точке
(производной функции f(х) в точке 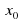 называют предел отношения приращения функции в точке
называют предел отношения приращения функции в точке 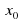 к приращению аргумента, если приращение аргумента стремится к нулю, а предел существует)
к приращению аргумента, если приращение аргумента стремится к нулю, а предел существует)
В чем заключается геометрический смысл производной?
(Значение производной f '(x) при данном значении аргумента 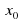 равно тангенсу угла, образованного касательной к графику функции в точке с абсциссой
равно тангенсу угла, образованного касательной к графику функции в точке с абсциссой 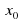 с положительным направлением оси Ox)
с положительным направлением оси Ox)
Как называется процесс нахождения производной?
(дифференцирование)
В чём заключается физический смысл производной?
( Производная функции у = f(х) в точке х0 выражает скорость изменения функции в этой точке )
Если некоторый процесс происходит по закону у= f(х), то как можно определить скорость протекания этого процесса в момент времени t?
(Найти производную от этой функции по времени)
Какие величины можно вычислять с помощью производной?
(углы наклона касательной к графику функции, скорость, ускорение, силу тока, мощность, теплоемкость, производительность труда, …)
Приведите примеры часто применяемых формул, содержащих производную (слайд 7):
| υ(t) = х ¢ (t) | Скорость – производная по времени от перемещения |
| a (t)=υ¢ (t) | Ускорение – производная от скорости |
| ω (t)= φ¢ (t) | угловая скорость- производная от угла поворота |
| а (t)= ω¢ (t) | угловое ускорение – производная от угловой скорости |
| I (t) = q¢ (t) | Сила тока- производная от количества электричества |
| N(t) = A¢ (t) | Мощность – производная от работы |
| c(t0) = Q¢ (t0) | Теплоемкость – производная от количества теплоты |
| Р(t) = V`(t) | Производительность труда – производная от объема продукции |
Итак, операция нахождения производной функции называется дифференцированием. С физической точки зрения – производная это скорость изменения переменной величины. Термин «скорость» настолько вошел в нашу жизнь, что мы порой не задумываемся над его смыслом и воспринимаем его только в связи с движением. На самом деле «скорость» характеризует зависимость изменения одной величины от изменения другой, что мы и видим в таблице.
Методический прием: «Страничка абитуриента» (приложение 1)
Для дальнейшей работы лаборатории необходимо актуализировать навыки практического вычисления производных. Для этого выполним следующее задание:
Найти соответствие между записанными функциями и их производными.
(индивидуальная работа с тестами в рабочих тетрадях по вариантам)
| 1 2 3 4 5 | А | Б | В | Г | Д | Е |
|
|
|
|
|
| х |
|
|
|
| х |
|
|
| х |
|
|
|
|
|
|
|
|
|
| х |
|
|
| х |
|
|
|
|
Взаимопроверка по записи на доске
| 1 2 3 4 5 | А | Б | В | Г | Д | Е |
|
|
|
|
| х |
|
|
|
|
| х |
|
|
|
| х |
|
|
|
|
|
|
| х |
|
|
|
| х |
|
|
|
|
|
Операционно-познавательная часть
Решение прикладных, проблемных задач
Методический прием «Решение задачи различными способами»
При подготовки к внешнему тестированию мы встретились с задачами, которые удобнее решать нахождением производной, чем другими известными способами. Рассмотрим на примере.
Задача (слайд 8)
Материальная точка движется прямолинейно по закону x(t)=-2+4t+3t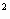 Найдите ее скорость и ускорение в момент времени t=2с. (х – координата точки в метрах, t – время в секундах).
Найдите ее скорость и ускорение в момент времени t=2с. (х – координата точки в метрах, t – время в секундах).
Решим данную задачу методами физики и математики
(два ученика решают у доски, учащиеся в классе – самостоятельно в тетрадях способом, которым лучше владеют. По окончании решения - обсуждение)
Решение
| Физический способ | Математический способ |
| x(t) = - 2 + 4t + 3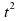 Так как x = 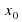 + + 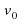 t + t + 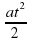 , то , то 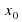 = - 2 м, = - 2 м, 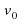 = 4м/с, а = 3 = 4м/с, а = 3 2 = 6м/с2. 2 = 6м/с2.
v = 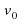 + at = 16м/с + at = 16м/с | x(t) = - 2 + 4t + 3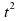 v(t) = x`(t) = 4 + 6t v(2) = 4 + 6  2 = 16 м/с 2 = 16 м/с a(t) = v`(t) = 6 м/с2 |
Вопрос:
Какое решение вам больше нравится? Почему?
Методический прием «Разноуровневые задания»
Для закрепления математического способа решения задач физики отдельные работники лаборатории получают индивидуальные исследовательские задания ( два учащихся у доски решают задачи – слайд 10, шесть – в рабочих тетрадях по карточкам. По окончании работы предусмотреть разбор задач , которые были решены на доске; индивидуальные задания в тетрадях проверяются после урока)
Время на решение - до окончания работы класса над следующей задачей (приложение 2, 3)
А мы с вами разберем задачу, подтверждающую один из фундаментальных законов физики
Задача (слайд 9)
Камень, брошенный вертикально вверх со скоростью 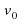 , находится в определенный момент времени t на высоте
, находится в определенный момент времени t на высоте 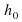 . Закон движения камня описывается формулой х =
. Закон движения камня описывается формулой х = 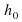 +
+ 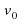 t -
t - 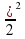 , где g = 10
, где g = 10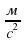 – ускорение свободного падения.
– ускорение свободного падения.
Докажите методами дифференциального исчисления, что полная энергия камня не зависит от времени
(разобрать решение на доске: 1 ученик, коллективное решение)
Решение:
Гипотеза - Полная энергия камня не зависит от времени, если является постоянной величиной, то есть производная по времени равна 0.
v(x) = x`(t) = 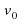 – gt .
– gt .
Е` = (Ек + Еп)` = (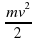 + mgh)` = (
+ mgh)` = (  + mg(
+ mg(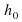 +
+ 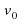 t -
t - 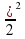 ))` =
))` =
= 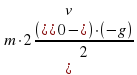 + mg(
+ mg(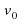 -
- 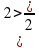 ) = - m
) = - m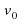 g + m
g + m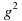 t + mg
t + mg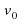 - m
- m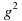 t = 0
t = 0
Вопрос:
какой закон физики подтвержден решением данной задачи
(закон сохранения механической энергии)
Методический прием «Решаем вместе»
Задача (короткая запись с помощью рисунка на доске).
Из пункта О по двум лучам, угол между которыми 60˚, движутся два тела: первое – равномерно со скоростью 5км/ч, которое – по закону s(t) = 2t² + t . С какой скоростью они удаляются друг от друга? (s измеряется в километрах, t – в секундах.)
Решение.
![]()

S1(t)=S(t)
 0 ) 600 S(t)
0 ) 600 S(t)
S2(t)=S(t)
По теореме косинусов:
s²(t) = (5t)² + (2t² + t)² - 2 · 5t · (2t² + t) · cos60˚ = 25t² + 4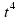 +4t³ + t² - 10t³ - 5t² = = 4t4 – 6t³ + 21t² ,
+4t³ + t² - 10t³ - 5t² = = 4t4 – 6t³ + 21t² ,
т.е. s(t) =t·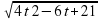 , где t 0.
, где t 0.
v(t) = s´(t) =( t·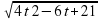 ,)´= t`
,)´= t` 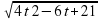 + t ·
+ t · 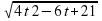 =
=
= 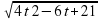 +
+  =
= 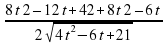 =
=  =
=
= 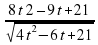 при t 0.
при t 0.
Практическая часть: решение исследовательских задач
(творческий поиск)
Методический прием: работа в группах(приложение 4)
Рассмотрим различные виды задач, при решении которых удобно применять производную.
Для создания творческой конкурентной работы наша лаборатория разделена на отделения. Каждому отделению предложены для решения практические задачи из различных отраслей знаний. Ваше задание – совместными усилиями решить данные задачи (слайд 11).
Итог этапа
Представители групп анализируют выполнение каждой задачи ( сообщают план решения, другие группы сверяются, правильно ли они выполняли задание)
Подведение итогов урока. Рефлексия
(подведение итогов работы)
Мы видим, что производная функции используется всюду, где есть неравномерное протекание процесса.
Мы сегодня повторили применений производной в физике, но возможности применения производной намного шире, в чем мы сегодня и убедились: ее можно применять при изучении многих вопросов по динамике, так же при изучении электромагнитных явлений, в оптических явлениях, при решении задач по ядерной физике. Те вопросы, которые мы сегодня рассмотрели, помогут вам при решении задач по математике и физике на ВНО
Вопрос:
Выразите свои впечатления от урока
Инструктаж по домашнему заданию
(задание на следующий день исследований)
Для закрепления материала, рассмотренного сегодня, вы проведете самостоятельные исследования дома: на выбор. Домашнее задание ориентировано на 2 группы учащихся: обязательный минимум выполнения + пространство для инициативных:
Я думаю, что вы поняли необходимость изучения темы «Производная» , увидели, как это может пригодиться на практике, и надеюсь, что знания, полученные в школе, пригодятся вам в жизни.
Спасибо за урок.
Лаборатория дифференциальных исчислений на сегодня закончила свою работу.
Приложение 1
«Страничка абитуриента»
Найти соответствие между записанными функциями и их производными.
Ответы впишите в таблицу
Вариант 1 Вариант 2
| 1. у = 5х | А. у`= 12 |
| 1. у = 8 | А. у`= - 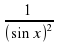 |
| 2. у =  | Б. у`=  | 2. у =  | Б. у`= 6х – 4 |
| 3. у = 6 | В. у`= 0 | 3. у = 3 – 4х+4 – 4х+4 | В. у`=  |
| 4. у = 6 | Г. у`= -  | 4. у = tg х | Г. у`= 12 |
| 5. у =  | Д. у`= 18 | 5. у = ctg х | Д. у`= 0 |
|
| Е. у`= 5 |
| Е. у`= 6х |
Таблица для ответов
Приложение 2
Индивидуальные задания
для самостоятельного решения в рабочих тетрадях
Задание: используя предложенный план решения, решите следующие задачи.
Задача 1
Тело движется по прямой так, что расстояние S (в м) от него до точки М этой прямой изменяется по закону S(t) = t4 +  t3 – t2 + 8. Чему будет равна мгновенная скорость (м/с) через 3 секунды после начала движения?
t3 – t2 + 8. Чему будет равна мгновенная скорость (м/с) через 3 секунды после начала движения?
План решения:
Найдем v(t) = s`(t)= (t4 +  t3 – t2 + 8)`= …
t3 – t2 + 8)`= …
Подставим в полученную формулу вместо t число 3.
Получим v(3) = …
Задача 2
Материальная точка движется по закону x(t) = t3 – t2 +9t +11
( х – перемещение в м, t – время в с). Через сколько секунд после начала движения ускорение точки будет равно 10 м/с2 ?
План решения:
Найдем v(t) = s`(t)= (t3 – t2 +9t +11)`= …
Найдем a(t) = v`(t) = …
Подставим в полученную формулу a(t) вместо а соответственно 10, решим полученное уравнение и найдем t
Приложение 3
Индивидуальные задания
для самостоятельного решения на доске
Задача 1
Концентрация некоторого вещества в крови человека вследствие его выведения из организма изменяется по закону: n(t) = 2е- 0,05t . Как изменяется скорость выведения вещества из организма с течением времени?
Решение:
Скорость выведения вещества из организма является производной по времени от концентрации этого вещества в крови человека, то есть
v(t) = n`(t) = 2е- 0,05t (-0,05t)`= 2е- 0,05t (-0,05)= -0,1е- 0,05t
Вопрос: что означает знак «-«?
(количество вещества в крови со временем уменьшается)
Задача 2
Известно, что для любой точки C стержня АВ длиной 20 см, отстоящей от точки А на расстояние l, масса куска стержня АС в граммах определяется по формуле m(l) = 3l² + 5l.
Найдите линейную плотность стержня: а) в середине отрезка АВ; б) в конце В стержня.
Решение
Линейная плотность стержня d(l) есть производная от массы по длине.
m(l) = 3l² + 5l; d(l) = m´(l) = (3l² + 5l)´ = 6l + 5.
Линейная плотность в середине отрезка АВ = 20 см: d(10) = 6 · 10 + 5 = 65 (г/см).
Линейная плотность в конце В отрезка АВ: d(20) = 6 · 20 + 5 = 125 (г/см).
Приложение 4
Задания для работы в группах
| Группа А Точка движется прямолинейно по закону x(t)=2t3+t-3. В какой момент времени ускорение будет равно 24 м/с2. (х – координата точки в метрах, t- время в секундах) В какие моменты времени сила тока в цепи равна 0А, если количество электричества, протекающего через поперечное сечение проводника, задается формулой q = t +  Количество радиоактивного вещества в момент времени t выражается формулой m = M   , где Т – период полураспада, М – первоначальное количество вещества. Найдите мгновенную скорость распада вещества в момент времени , где Т – период полураспада, М – первоначальное количество вещества. Найдите мгновенную скорость распада вещества в момент времени  . .
|
| ГруппаБ Вращение тела вокруг оси совершается по закону  (t) = 3t² -4t +2. Найти угловую скорость (t) = 3t² -4t +2. Найти угловую скорость  (t) и угловое ускорение а(t) при t =4c.( (t) и угловое ускорение а(t) при t =4c.(  (t) – угол в радианах, (t) – угол в радианах,  (t)- скорость в радианах в секунду, t- время в секундах) (t)- скорость в радианах в секунду, t- время в секундах) Две материальные точки движутся прямолинейно по законам S1(t) = 2,5t2 - 6t + 1 S2(t) = 0,5t2 +2t - 3 В какой момент времени tо скорости их равны, т.е. v1(tо)=v2(tо)? Зависимость между массой вещества М, получаемого в химической реакции и временем t выражается уравнением: М(t) = Аt2 +Bt, где А и В – постоянные. Какова скорость реакции? |
| Группа В Колебательное движение точки описывается уравнением х=0,05cos20 t. Найти проекцию скорости и проекцию ускорения спустя t. Найти проекцию скорости и проекцию ускорения спустя  с. с. Количество электричества, протекающего через проводник, начиная с момента времени t = 0, задается формулой q = 3t² + t + 2. Найдите силу тока в момент времени t = 3. Конденсатор ёмкостью C и зарядом q0 разряжается через резистор R по закону: q = q0  Найти скорость изменения заряда конденсатора. Какова скорость в начале разряда (t = 0)? Найти скорость изменения заряда конденсатора. Какова скорость в начале разряда (t = 0)?
|
| Группа Г Тело массой 4 кг движется прямолинейно по закону х(t) = t2 +t + 1. Какова кинетическая энергия тела в конце третьей секунды движения после начала движения? Найдите силу F, действующую на материальную точку с массой m, движущуюся прямолинейно по закону x(t)=2t³- t² при t=2. Напряжение на конденсаторе ёмкостью C = 0,5 мкФ изменяется по закону: u = 10sin (100![]() t). Найти как изменяется со временем сила тока через конденсатор. t). Найти как изменяется со временем сила тока через конденсатор.
|
Приложение 5
Тестовые задания по теме
«Применение производной в различных областях науки и техники»
1) Скорость точки, движущейся по прямой по закону x(t) =  t3-5t2, равна
t3-5t2, равна
| А | Б | В | Г | Д |
|  t3-5t2 t3-5t2
|
t3- 5t |
t2-10t |  t2-10t t2-10t
|
t4-5t. |
Точка движется по прямой по закону s(t) =2t2-2t-1. Её мгновенная скорость v(3) равна
Ускорение точки, движущейся по прямой по закону s(t) =t3-5t2 равно:
| А | Б | В | Г | Д |
| 2(3t-5) |
| 6t-8 | 9t2-10 | . 3t2-8t |
Тело массой m движется по закону x(t) =3cos3 t. Сила, действующая на тело в момент времени t =
t. Сила, действующая на тело в момент времени t =  равна:
равна:
| А | Б | В | Г | Д |
| 0 | 27 2m 2m | 9 2m 2m | 9m | 27m |
Скорость точки, движущейся по прямой по закону x(t) =  t2-4t, равна
t2-4t, равна
| А | Б | В | Г | Д |
|  t-4t t-4t
|
t- 4t |  .t3-4t2 .t3-4t2
|
t-4 | . t3-4t2 |
Точка движется по прямой по закону s(t) =4t2-5t+7. Её мгновенная скорость v(2) равна
| А | Б | В | Г | Д |
| 11 | 13 | 12 | 10 | 11. |
Ускорение точки, движущейся по прямой по закону s(t) =-t3+2t2 равно:
| А | Б | В | Г | Д |
| 6-6t | 2(2-3t) | -3t2+4t | -3t+4 | -3t2+4. |
Тело массой m движется по закону x(t) =-2sin2 . Сила, действующая на тело в момент времени t=
. Сила, действующая на тело в момент времени t= равна:
равна:
| А | Б | В | Г | Д |
| 0 | 8m | 8 2m 2m | 4 2m . 2m . | 4m .. |
Скорость точки, движущейся по прямой по закону x(t) =3 t3+2t2, равна
| А | Б | В | Г | Д |
| 9t2 +4 t | 3t2 +2t | 9t2+2t | 3t4+2t3 | 3t4+2. |
Точка движется по прямой по закону s(t) =-t2+10t-7. Её мгновенная скорость v(1) равна
Ускорение точки, движущейся по прямой по закону s(t) =  t3-6t равно:
t3-6t равно:
| А | Б | В | Г | Д |
| t2 -6 | 3t-1 | 2t | 2t-6 | t2-6t. |
Тело массой m движется по закону x(t) =2sin4 . Сила, действующая на тело в момент времени t=
. Сила, действующая на тело в момент времени t= равна:
равна:
| А | Б | В | Г | Д |
| 0 | 16 m m | 16m | -32 2m 2m | 16. |
Скорость точки, движущейся по прямой по закону x(t) =2 t3+ t2, равна
t2, равна
| А | Б | В | Г | Д |
| 2t2+  t t | 6t2 +0,5t | 6t2+ t t | 6t2+ 0,5 | 6t + 0,5. |
Точка движется по прямой по закону s(t) =3t2+2t-1. Её мгновенная скорость v(3) равна
Тело массой движется по закону x(t) =-3cos2 . Сила, действующая на тело в момент времени t=
. Сила, действующая на тело в момент времени t= равна:
равна:
| А | Б | В | Г | Д |
| -12 m m | 0 | -12m | 12m | -12 . . |
Материальная точка движется по закону  (х– перемещение в м, t – время в с). Через сколько секунд после начала движения ускорение точки будет равно 10м/с2?
(х– перемещение в м, t – время в с). Через сколько секунд после начала движения ускорение точки будет равно 10м/с2?
Материальная точка движется по закону  (х –перемещение в м, t – время в с). Через сколько секунд после начала движения ускорение точки будет равно 8м/с2?
(х –перемещение в м, t – время в с). Через сколько секунд после начала движения ускорение точки будет равно 8м/с2?
Тело движется по прямой так, что расстояние S(в м) от него до точки М этой прямой изменяется по закону  . Чему будет равна мгновенная скорость (м/с) через 4 секунды после начала движения?
. Чему будет равна мгновенная скорость (м/с) через 4 секунды после начала движения?
| А | Б | В | Г | Д |
| 123 | 111 | 108 | 121 | 116 |
Тело движется по прямой так, что расстояние S(в м) от него до точки М этой прямой изменяется по закону S(t)=5t2-3t+6. Через сколько секунд после начала движения произойдет остановка?
В чем сущность физического смысла производной?
| А | Б | В | Г | Д |
| Скорость | Ускорение | Угловой коэффициент | Сила | Другой ответ |
Точка движется по закону S(t) = 2t2 -3t Чему равна скорость в момент tо = 1с?
Точка движется прямолинейно по закону S(t) = t3/3 -2t2+3t+1. В какие моменты времени скорость будет равна нулю?
| А | Б | В | Г | Д |
| 1 и 3 | 1 и 4 | 2 | 2 и 0 | 2 и 4 |
Скорость тела, движущегося прямолинейно, определяется по формуле v(t) = 5t3 + t2 Чему равно ускорение тела в момент времени tо=1с
Скорость тела,движущегося прямолинейно,определяется по формуле v(t) = 15t2 + 2t Чему равно ускорение тела в момент времени tо=1с
Приложение 6
Цикл задач
«Применение производной в различных областях науки и техники»
По прямой движутся две материальные точки по законам  = 4
= 4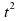 - 5 и
- 5 и  =
= 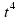 . В какой промежуток времени скорость первой точки будет больше скорости второй точки?
. В какой промежуток времени скорость первой точки будет больше скорости второй точки?
Точка совершает гармонические колебания по закону х = 15 . Найти мгновенную скорость точки в момент времени
. Найти мгновенную скорость точки в момент времени  .
.
Найдите скорость и ускорение точки, движущейся по закону s(t) = 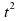 + 2t +3 в момент времени t = 3с.
+ 2t +3 в момент времени t = 3с.
Маховик, задерживаемый тормозом, за время t поворачивается на угол  . Найдите такой момент времени, когда маховик остановится. (углы – в рад, время – в с)
. Найдите такой момент времени, когда маховик остановится. (углы – в рад, время – в с)
Точка движется прямолинейно по закону X(t)=2t²+t-1. В какой момент времени ускорение будет равно 2см/с². Х(t)- перемещение в метрах, t- время в секундах)
Найдите силу F, действующую на материальную точку с массой m = 2кг, движущуюся прямолинейно по закону x(t)=2t³-t² при t=2.
Частица совершает гармонические колебания по закону х=24cos t см. Определите проекцию скорости частицы на ось х в момент времени t = 4с.
t см. Определите проекцию скорости частицы на ось х в момент времени t = 4с.
Материальная точка движется прямолинейно по закону х(t)=18t2 – t3 (x- в метрах, t- в секундах). Определите, в какой момент времени из промежутка [4;8] скорость точки будет наибольшей и найдите в это время ускорение.
Материальная точка движется прямолинейно по закону x(t)=t3-4t². Найти скорость и ускорение в момент t=5c. (Перемещение измеряется в метрах)
Точка движется прямолинейно по закону x(t)=-t³/6+3t²-5 (координата в метрах, t- время в секундах). Найти: а) момент времени t, когда ускорение точки равно нулю; б) скорость движения точки в этот момент.
Точка движется прямолинейно по закону х(t)= . Покажите, что ее ускорение пропорционально кубу скорости.
. Покажите, что ее ускорение пропорционально кубу скорости.
Тело массой 2 кг движется прямолинейно по закону x(t)=t²+t+1. Координата х измеряется в сантиметрах, время t – в секундах. Найдите: а) действующую силу; б) кинетическую энергию Е тела через 2 с. после начала движения.
Два тела совершают прямолинейное движение по законам S (t) = 3t
(t) = 3t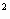 -2t+10, S
-2t+10, S (t) = t
(t) = t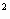 +5t+1, где t – время в секундах, а S
+5t+1, где t – время в секундах, а S (t), S
(t), S (t) – пути в метрах, пройденные, соответственно, первым и вторым телами. Через сколько секунд, считая от t=0, скорость движения первого тела будет в два раза больше скорости движения второго тела?
(t) – пути в метрах, пройденные, соответственно, первым и вторым телами. Через сколько секунд, считая от t=0, скорость движения первого тела будет в два раза больше скорости движения второго тела?
Тело движется по закону S(t) = 3t3 – 12t2 + t +47. Определите скорость в произвольный момент времени.
Материальная точка движется со скоростью v(t) =2t2 – 3t. Найдите закон изменения пути от времени.
Тело движется по закону s(t)=t3+2t2+4t+1. Найдите расстояние, пройденное телом от начала движения до того момента, когда ускорение стало равно 10м\с2.
Тело массой 4 кг движется прямолинейно по закону х(t) = t2 +t + 1. Какова кинетическая энергия тела в конце третьей секунды движения после начала движения и сила, действующая на тело?
Конденсатор ёмкостью C и зарядом q0 разряжается через резистор R по закону: q = q0  Найти скорость изменения заряда конденсатора. Какова скорость в начале разряда (t = 0)?
Найти скорость изменения заряда конденсатора. Какова скорость в начале разряда (t = 0)?
В двухэлектродной лампе сила анодного тока зависит от анодного напряжения по закону: I(U) =  , где
, где  - постоянная, зависящая от формы, размеров, расположения электродов. Получить формулу прироста тока на каждую единицу изменения напряжения.
- постоянная, зависящая от формы, размеров, расположения электродов. Получить формулу прироста тока на каждую единицу изменения напряжения.
Каково изменение периода колебаний математического маятника при изменении его длины?
Заряд на пластинах конденсатора колебательного контура с течением времени изменяется по закону: q = 10-6  . Записать уравнение зависимости силы тока от времени.
. Записать уравнение зависимости силы тока от времени.
Теплоемкость воды при t = 100оС равна 1,013. Количество теплоты, необходимое для нагревания 1 кг воды от 0оС до tоС, определяется формулой Q = t + 2 × 10-5t2 + 3a × 10-7t3. Найдите значение параметра а.
Напряжение на конденсаторе ёмкостью C = 0,5 мкФ изменяется по закону: u = 10sin (100![]() t). Найти как изменяется со временем сила тока через конденсатор.
t). Найти как изменяется со временем сила тока через конденсатор.
Заряд на пластинах конденсатора колебательного контура с течением времени изменяется по закону: q = 10-6sin104![]() t. Записать уравнение зависимости силы тока от времени.
t. Записать уравнение зависимости силы тока от времени.
Точка движется по – прямой так, что ее скорость в момент времени t равна V(t) = t2 – t + 1. известно, что в начальный момент времени t = 0 точка имеет координату (-1). Найти координату и ускорение точки в момент времени t.
Тело массой 3 кг движется прямолинейно по закону x(t) = 2t2 + t + 5, координата x измеряется в сантиметрах, время t – в секундах. Найти кинетическую энергию Е тела через 3 сек. после начала движения.
Материальная точка движется прямолинейно по закону x(t) = t2 – 4t + 3. Выведите формулу для вычисления скорости движения в любой момент времени t.
Точка движется по закону x(t) = t3 + 1. Найти ускорение в момент времени t = 1c
Координата материальной точки изменяется с течением времени по закону х(t) = 3t2 - 7t + 6. Найдите скорость точки в момент времени t = 6.
При движении тела по прямой его скорость V (м/с) меняется по закону V ( t ) = t 5 /5 - t 3 + t + l , где t - время движения в секундах. Найдите ускорение (м/с 2) через 2 секунды после начала движения.
В какие моменты времени ток в цепи равен нулю, если количество электричества, протекающего через проводник, задается формулой: а) q = t + 4/ t
2
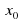 называют предел отношения приращения функции в точке
называют предел отношения приращения функции в точке 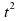
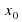 +
+ 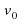 t +
t + 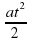
 2 = 6м/с2.
2 = 6м/с2.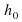 . Закон движения камня описывается формулой х =
. Закон движения камня описывается формулой х = 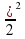
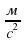 – ускорение свободного падения.
– ускорение свободного падения. 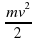 + mgh)`
+ mgh)`
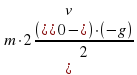 + mg(
+ mg(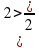 ) = - m
) = - m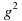 t + mg
t + mg
 0 ) 600
0 ) 600 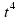 +4
+4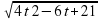 , где
, где 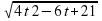
 =
= 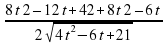 =
=  =
=