Практическое занятие по теме "Матрицы. Определители второго и третьего порядков"

Практическое занятие №1

Тема: «Действия над матрицами. Определители второго и третьего порядка»

Цели: закрепить основные понятия теории матриц; формировать умения и навыки выполнять операции над матрицами; вычислять определители второго и третьего порядков.

Содержание работы

Матрицы. Основные понятия.

Матрицей называется прямоугольная таблица чисел.

Пример 1. , , , .

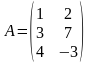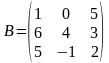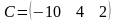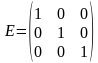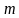В общем случае матрица может содержать строк и 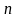столбцов

.

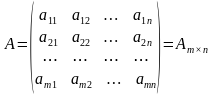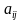Числа называются элементами матрицы, где 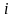- указывает номер строки, 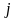- указывает номер столбца.

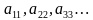Элементы образуют главную диагональ матрицы.
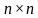Если число строк равно числу столбцов, то матрица называется квадратной. Квадратная матрица размеров называется матрицей – го порядка.

Квадратная матрица, у которой все элементы, кроме главной диагонали равны 0, называется диагональной.

Пример 2. .

Если все элементы матрицы равны нулю, то матрица называется нулевой.

Пример 3. .

Диагональная матрица, у которой каждый элемент диагонали равен 1, называется единичной.

Пример 4. , .

Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от диагонали, равны нулю.

Пример 5. , .

Матрица, содержащая одну строку (столбец), называется вектором (вектор-строкой, вектор-столбцом).

Пример 6. , .

Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется транспонированной .

Пример 7. ;

Очевидно, что .

Действия над матрицами.

Матрицы одинаковых размерностей можно складывать и вычитать. Если

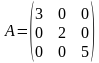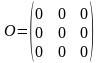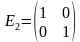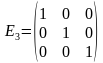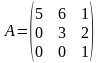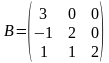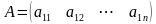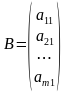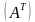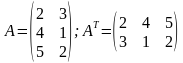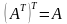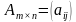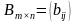, , то 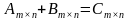, причем

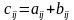, для всех .

Пример 8. ,

.

Умножение матрицы на число.

Чтобы умножить матрицу на число, необходимо каждый ее элемент умножить на это число.

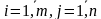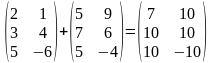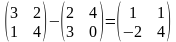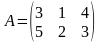Пример 9. Пусть , тогда .
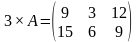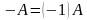Матрица называется противоположной к матрице .

Умножение матриц.

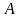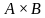Умножение матриц можно только в том случае, когда число столбцов матрицы 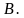равно числу строк матрицы В этом случае справедливо соотношение 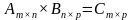, причем элементы матриц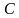ы равны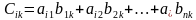 , , 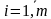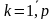.Другими словами строки матрицы умножаются на столбцы матрицы

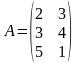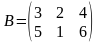Пример 10. Пусть , . Тогда

,

.

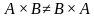Видим, что в общем случае . Если же выполняется условие , то матрицы и называются перестановочными друг с другом.

Контрольные вопросы

1. Что такое матрица? Как определяется размерность матрицы?

2. Сформулируйте определение квадратной матрицы. Приведите пример.

3. Какие элементы матрицы образуют главную диагональ? Побочную диагональ?

4. Сформулируйте определение единичной матрицы. Приведите пример.

5. Сформулируйте определение диагональной матрицы. Приведите пример.

6. Какая матрица называется транспонированной? Приведите пример.

7. Всегда ли можно выполнить сложение (вычитание) двух матриц?

8. При каком условии возможно выполнить умножение матриц?

Определители.

Определителем называется квадратная числовая таблица, вычисляемая по определенным правилам.

Если , то . Так .

Если , то .

Так .

Если , то

. Так

.

При вычислении определителей 3-го порядка удобно пользоваться правилом треугольников. С плюсом берутся произведения элементов стоящих на главной диагонали и элементы, стоящие в вершинах следующих треугольников.

С минусом берутся произведения элементов, стоящих на второй диагонали и в вершинах следующих треугольников.

Второй метод заключается в том, что рядом с определителем справа записываются первый и второй столбцы и тогда с плюсом берутся произведения элементов, стоящих на главной диагонали и двух ей параллельных, с минусом – произведения элементов, стоящих на второй диагонали и двух ей параллельных.

Вычисление определителей более высоких порядков осуществляется путем использования их свойств.

Из элементов этой матрицы можно составить определитель, который называется детерминантом матрицы и обозначается

Минором некоторого элемента определителя называют определитель, который получается вычеркиванием из него строки и столбца. Например

1. , .

Алгебраическим дополнением элемента определителя называют число . Например

, .

Определитель равен сумме произведений элементов какой-нибудь его строки (столбца) на их алгебраические дополнения. Например

.

Задания для самостоятельного выполнения.

Задание №1. Для матриц А и В найдите: а) ; б) 4В- 3A

Задание №2. Вычислите определители матриц А и B, если:

Задание №3. Даны матрицы А и В. Найдите матрицу C=A·B