Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке.

В разработке представлен урок по §46.п.1. Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке. Профильный уровень.10 класс”.

Урок проводится с целью изучения и первичного закрепления материала по теме “ Наибольшее и наименьшее значения функции на промежутке”, как одной из основных тем по исследованию функций. Это первый урок из четырёх по теме “Применение производной для нахождения наибольших и наименьших значений величин” и рассчитан на 1 час учебного времени. По ходу урока акцент делается на изучение и отработку как общих методов решения задач (по известному алгоритму), так и перевод задачи на другой язык (использование свойств функций).

Тип урока: урок изучения нового материала с использованием ИКТ.

Оборудование и материалы для урока: компьютерный класс, проектор, интерактивная доска, презентация для сопровождения урока, карточки-бланки для ответов учащихся, карточки-инструкторы для проведения работы.

Цель: познакомить учащихся с приемами нахождения наибольшего и наименьшего значения функции на промежутке.

Задачи.

Образовательная - повторить необходимые и достаточные условия существования точек экстремума, понятия: стационарная и критическая точка; вывести алгоритм нахождения наименьшего и наибольшего значений функции, формировать умения решать задачи на отыскание наибольших и наименьших значений функции.

Развивающая – развивать познавательный интерес обучающихся, умение исследовать, выделять главное, сравнивать, анализировать, делать выводы.

Воспитательная – воспитывать умения работать в сотрудничестве в парах и группе, оценивать работу товарища.

Знания, умения, навыки и качества, которые актуализируют/приобретут/ закрепят/ др. ученики в ходе урока:

- овладение практическими умениями и навыками по теме “Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке”

- умение устанавливать причинно-следственные связи, выделять главное, обобщать, систематизировать;

- формирование навыков самостоятельной работы с учебным материалом;

- формирование навыков самоконтроля.

Структура урока.

Ход урока

1. Оргмомент.

Организация групп (до урока). Приветствие. Эпиграф к уроку (слайд 1).

2. Актуализация знаний.

Устная работа (слайды 2-4). Повторение материала, изученного на предыдущих уроках. Фронтальная работа. Учитель обращает внимание обучающихся на существенное различие понятий максимума (минимума) функций и наибольшего (наименьшего) значений.

3. Мотивация.

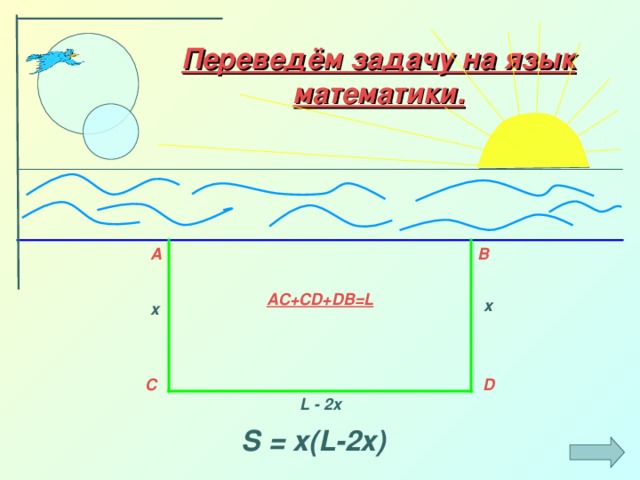
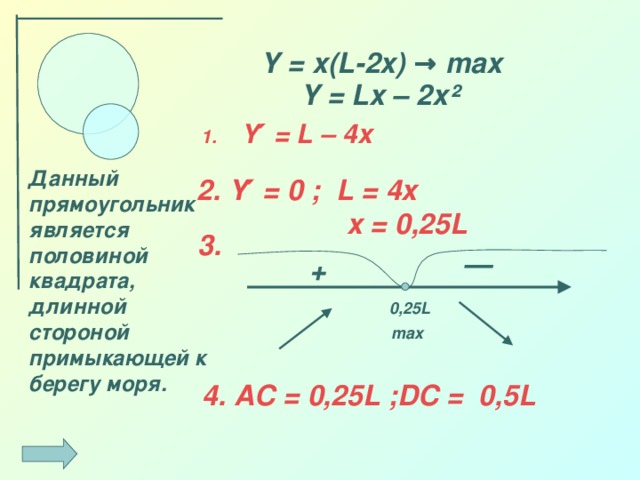
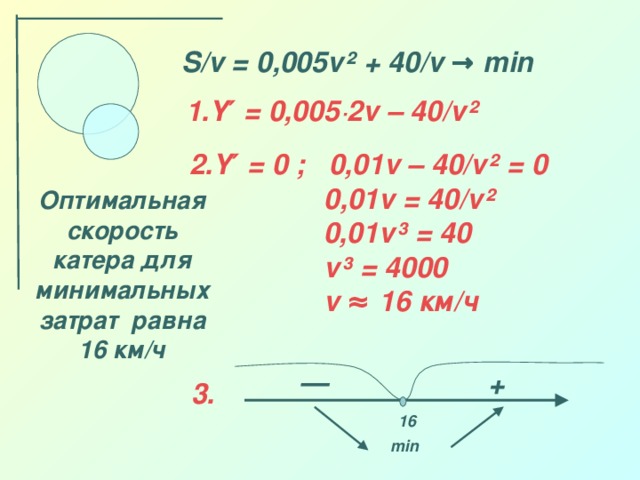
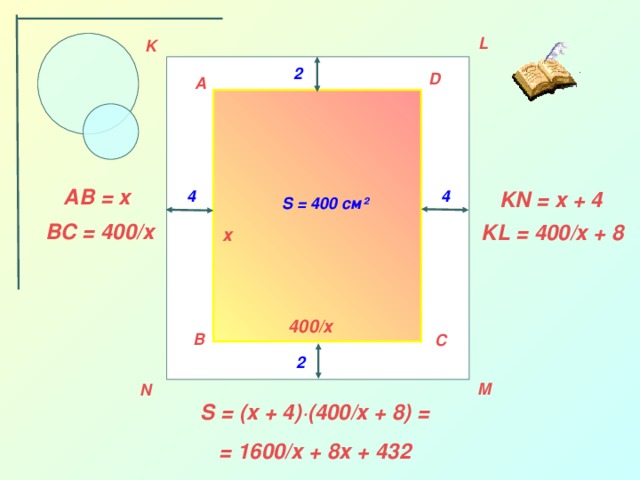
Нахождение наибольшего и наименьшего значений функции широко применяется при решении многих практических задач на нахождение наилучших, оптимальных решений при наименьших затратах труда, так называемые задачи на оптимизацию.

С некоторыми из таких задач мы познакомимся на следующих уроках. Чтоб успешно решать такие задачи необходимо уметь находить наибольшее и наименьшее значения заданных функций на заданном промежутке.

Постановка обучающимися темы и целей урока (слайд 6-7).

4. Изучение нового материала. Первичное осмысление.

Ребятам предлагается три графика функции для самостоятельного определения точек наибольшего и наименьшего значений. Проанализировать расположение данных точек на графике и сделать вывод (слайд 8). Работа выполняется по группам. Если возникают затруднения, то можно воспользоваться карточкой-инструкцией. (Приложение 1)

Затем спикер одной из групп высказывает мнение своей группы, а остальные сравнивают его со своим мнением, дополняют или уточняют, возможно, опровергают. В итоге обучающиеся делают вывод (слайд 9).

Постановка проблемы.

Учитель задает вопрос: “Как, не изображая графика функции, определить наибольшее и наименьшее значение функции на отрезке?”

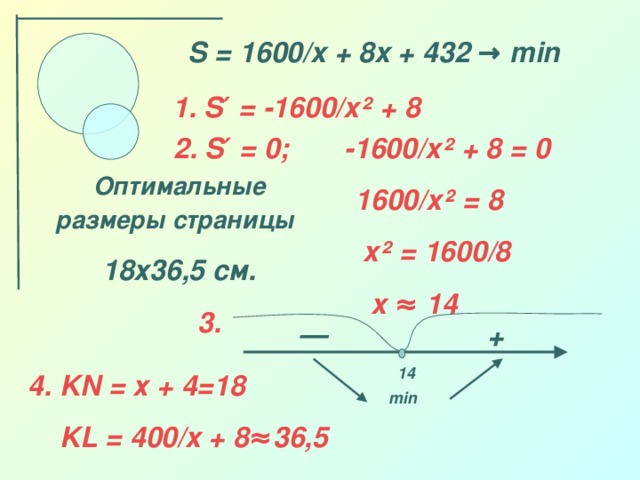
Задание 1. Найти наибольшее и наименьшее значение функции у = х3 - 3х2 - 45х + 1 на [-4; 6] без построения графика. (Слайд 10). Ребята предлагают решение. Учитель корректирует работу, задавая наводящие вопросы. Решение оформляется на доске в интерактивном режиме учителем.

Ответ: у наим = у (5) = -174; у наиб = у(-3) = 82.

Задание 2. (Слайд 11) Выполнить задание, рассуждая аналогично. Задание на репродуктивном уровне выполняется самостоятельно.

Ответ: у наим = у (-1) = -13; у наиб = у(1) = 3

Задание 3. Проанализировать решения предыдущих примеров и сформулировать алгоритм нахождения наименьшего и наибольшего значений функции на отрезке. Обучающиеся вновь по группам обсуждают данный вопрос, затем, обменявшись мнениями с другими группами, приходят к общему выводу.

Решение проблемы.

Ребята формулируют алгоритм. Проверяется алгоритм по учебнику стр.371 (слайд 12). (Ситуация успеха).

Учитель дополняет. Если речь идет о нахождении наибольшего или наименьшего значений функции, непрерывной на незамкнутом промежутке, то удобно использовать следующую теорему (слайд 13). Данная теорема в курсе 10 класса не доказывается. Ребята записывают теорему в тетрадь.

5. Закрепление “добытых” знаний.

При подготовке к уроку учитель делает закладку необходимой для занятия Web-страницы. Интернет-сайт “ЕГЭ по математике: подготовка к тестированию” http://www.uztest.ru. включает “Тренажер”, позволяющий проходить on-line тест по теме “Наибольшее, наименьшее значение функции” на конструктивном уровне. Ребятам предлагается выполнить тест из 5 заданий. Верные ответы заносятся в таблицу (Приложение 1). Осуществляя дифференцированный подход к обучающимся, предлагаются дополнительные примеры из учебника № 46.20(а), №46.21(а).

6. Итог. Рефлексия деятельности на уроке. Домашнее задание.

Учитель беседует с ребятами, говоря о новых знаниях полученных на уроке, о достигнутых целях, интересуется их ощущениями от происходящего и предлагает заполнить карточки рефлексии. (Приложение 1)

Домашнее задание. §46.п.1. Каждый ученик получает индивидуальное разноуровневое задание на сайте http://www.uztest.ru. Для входа на личную страницу учитель сообщает логин и пароль для каждого ученика. Оценки выставляются в электронный журнал.