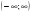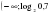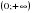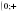Государственное областное бюджетное
профессиональное образовательное учреждение
«ЛИПЕЦКИЙ ПОЛИТЕХНИЧЕСКИЙ ТЕХНИКУМ»
Методическая разработка
урока математики
«Показательные неравенства».
Выполнил:
преподаватель математики
Заварзина В.Г.
Липецк 2016 г.
Тема урока:
«Показательные неравенства».
Цели урока:
1. Образовательные:
а) обобщение и применение свойств показательной функции при решении неравенств;
б) научить применять полученные знания при решении заданий различного уровня сложности.
2. Развивающие:
развивать логическое мышление, память, познавательный интерес, продолжать формирование математической речи, вырабатывать умение анализировать.
3. Воспитательные:
приучать к эстетическому оформлению записей в тетради, воспитывать трудолюбие.
Тип урока: урок закрепления и совершенствования знаний
Методические приемы:
-самостоятельная работа (работа с раздаточным материалом);
Оборудование и наглядные средства обучения: компьютер, классная доска, слайдовая презентация, интерактивная доска, учебник «Алгебра и начала анализа10-11» под редакцией А.Г.Мордковича, чертёжные инструменты, Методическая цель: активизировать мыслительную деятельность обучающихся.
Ход урока:
I.Организационный момент: подготовка студентов к уроку (проверка отсутствующих на уроке, наличие тетрадей, проверка готовности рабочих мест студентов и преподавателя, готовности обучающихся к работе.)
На первом этапе преподаватель приветствует студентов, проверяет готовность группы к работе.
II.Постановка цели.
Сегодня на уроке мы продолжим отрабатывать навыки решения показательных неравенств, но попробуем постепенно повышать уровень сложности, познакомимся с другими подходами к их решению.
III.Проверка домашнего задания.
На дом вам было предложено решить три неравенства. Посмотрим ваше решение. (Преподаватель вызывает по желанию трех человек к доске,
параллельно проводит фронтальную беседу по теоретическим вопросам. Выставляет оценку за домашнее задание.)
3 студента работают у доски
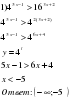 возрастает, т.к. 41
возрастает, т.к. 41

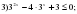
Введём новую переменную
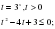
Решим квадратное уравнение
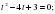
По свойству коэффициентов находим
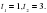
Решением неравенства является :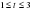
Возвратившись к исходной переменной, получаем:
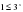
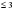 ,у=3х возрастает т.к. 31
,у=3х возрастает т.к. 31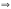
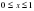
Ответ: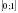 .
.
Студенты принимают участие в устном теоретическом опросе.
1.Что называется показательными неравенствами? ( Показательными называются неравенства, в которых неизвестное содержится в показателе степени.)
2.На чём основывается решение показательных неравенств?( На свойствах показательной функции.)
3.Перечислите эти свойства.( при а0,а 1
1
1)ах0 при всех а0 и х R
R
2)при а1 функция y=ах возрастает, т.е. если
а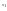 а
а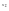
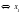
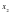
3) при 0ay=ах убывает, т.е. если
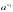
 )
)
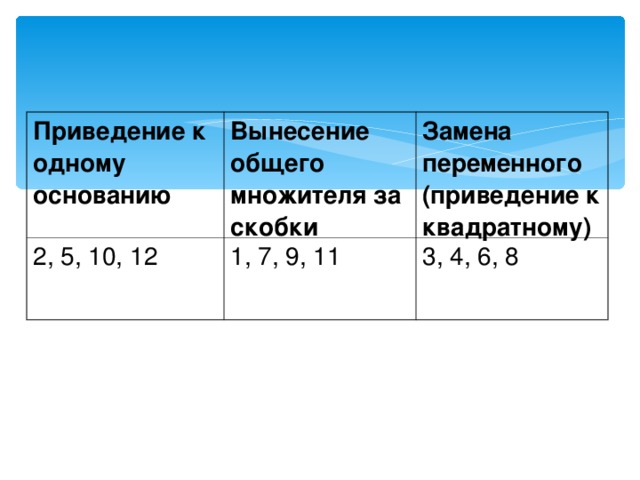
4.Какие приёмы используются при решении показательных неравенств?( 1)Неравенства, сводящиеся к простейшим, решаются приведением обеих частей неравенства к степени с одинаковым основанием.
2)Неравенства, решаемые с помощью вынесения за скобки общего множителя.
3)Неравенства, решаемые с помощью замены переменной.)
IV.Устные упражнения.
(До начала урока на обратной стороне доски записывает их. Следит за правильностью ответов. По возможности старается привлечь слабых студентов.)
Устные упражнения
| Задание | Ответ |
5х 125 0,5х 0,25 4х  1 1 0,3x 1 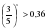
4x 3x 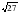 2,1x 0 18x 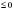 2x 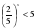
0,8 x 4,2x 1 43x -1 0,2x | x3 , 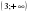 x 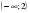  x 0 , 0 ,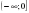 x 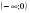 x 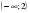
x 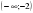 x1,5 , 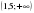 x , , 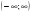 нет решений, пустое множество x ,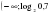 ) ) 11. x log , , 
12. x 0 , 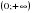 13. x 0 , 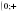 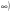 14. x , , 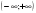 15.нет решений , пустое множество |
V.Закрепление ранее изученного материала.
(Один студент решает у доски, а остальные, в случае затруднения, предлагают методы решения. Конспектируют в тетрадях.)
1.
 ;
;
Так как 21, то это неравенство равносильно неравенству:
2x2+3x+2x2 ,
x2+3x+2
По виду неравенства составим уравнение:
x2+3x+2=0
По теореме, обратной теореме Виета, получаем
 х=-1 или х=-2
х=-1 или х=-2
Решением неравенства является
-2
Ответ: (-2;-1)
2.

Так как 9х0 , то имеем

Ответ: [-3;3]
3.

Разделив обе части неравенства на  , получаем
, получаем
Введём новую переменную 

так как t0
 По виду неравенства составим уравнение.
По виду неравенства составим уравнение.
VI.Совершенствование знаний.
(Студенты конспектируют в тетрадях.)
Ребята, сейчас мы вместе сформулируем свойства неравенств, содержащих степени и примем их без доказательства, так как они доказываются аналогично соответствующим свойствам логарифмов.
Теорема 1.
При всех допустимых значениях аи b справедливы следующие утверждения:
1)неравенства ab1 и(a-1)b0 равносильны;
2) неравенства  и (a-1)b≥0 равносильны;
и (a-1)b≥0 равносильны;
3)неравенства aba-1)b
4) неравенстваab≤1 и (a-1)b≤0 равносильны;
Теорема 2.
При всех допустимых значениях a,b и с справедливы следующие утверждения:
1)неравенства abac и (а-1)(b-c)0 равносильны;
2) неравенства ab≥ac и (а-1)(b-c)≥ 0 равносильны;
3) неравенства abacи (а-1)(b-c)
4) неравенства ab≤ac и (а-1)(b-c)≤ 0 равносильны;
Следствие.
При всех допустимых значениях a,b и с справедливы следующие утверждения:
1)неравенства ab-ac0 и (a-1)(b-c)0 равносильны;
2) неравенства ab-ac≥0 и (a-1)(b-c)≥0 равносильны;
3) неравенства ab-aca-1)(b-c)
4) неравенства ab-ac≤0 и (a-1)(b-c)≤0 равносильны;
VII.Решение заданий на закрепление.
(Студенты работают у доски по желанию.)
1.Решите неравенство: 










Ответ:

 2.Решите неравенство:
2.Решите неравенство:














Ответ:
 (0;1).
(0;1).
VIII.Тестирование.
(Студенты самостоятельно работают.)
ВариантI
1.Определите промежуток, который является множеством решений неравенства:






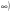


2.Решите неравенство:

3.Найдите все такие t, что 
Вариант II
1.Определите промежуток, который является множеством решений неравенства:

 б)
б)





2.Решите неравенство:


3.Найдите все такие t, что 
Ответы
Вариант I
1. 1) б
2) а
2. [-3;1]
3. (-1;+ )
)
Вариант II
1. 1) б
2) б
2. (- ;-2]
;-2] [1;+
[1;+ )
)
3. (-1;+ )
)
IX.Домашнее задание.
(Преподаватель поясняет домашнее задание, обращая внимание студентов на то, что аналогичные задания были разобраны на уроке. Студенты внимательно прослушав пояснение преподавателя, записывают домашнее задание)
№1.
y=2t -возрастающая функция, т.к. 21

Ответ: ( - ;4,5)
;4,5)
№2
D0-2 решения.
t=3 или t=

Ответ: (-1;1)
Задание для сильных учащихся
При каких значениях а уравнение имеет один корень.
25х-(а+1)5х+3а-6=0;
5х=t, t0; t2-(a+1)t+(3a-6)=0; D=(a+1)2-4(3a-6)=(a-5)2;Уравнение имеет один корень, если D=0 или в случае, когда корни имеют разные знаки, т.е. 3а-6
Ответ: при а=5 и а
X.Подведение итогов урока.
Решение показательных неравенств требует от учащихся хороших теоретических знаний, умений применять их на практике, требует внимания, трудолюбия, сообразительности. Именно по этой причине неравенства, аналогичные рассмотренным на уроке, выносятся на итоговую аттестацию. Сегодня на уроке все очень хорошо поработали. Молодцы!
Выставление оценок.
Список литературы:
1. Дидактические материалы по алгебре и началам анализа для 11 класса /Б.М. Ивлев, С.М. Саакян, С.И. Шварцбурд. – М.: Просвещение, 2003.
2. Алгебра и начала анализа: Учеб. для 10–11 кл. общеобразовательных учреждений / А.Н. Колмогоров, А.М. Абрамов, Ю.П. Дудницын и др.; Под. ред. А.Н. Колмогорова. – М.: Просвещение, 2004.
3. Алгебра и начала математического анализа. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных . учреждений (профильный уровень)/А.Г. Мордкович и др. ; под редакцией А.Г. Мордковича—7-е изд., стер.—М.: Мнемозина, 2014.
4. Задачи по алгебре и началам анализа: Пособие для учащихся 10–11 кл. общеобразоват. учреждений /С.М. Саакян, А.М. Гольдман, Д.В. Денисов. – М.: Просвещение, 2003.
5
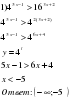 возрастает, т.к. 41
возрастает, т.к. 41
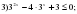
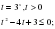
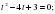
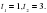
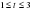
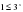
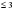 ,у=3х возрастает т.к. 31
,у=3х возрастает т.к. 31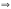
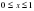
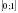 .
. 1
1
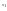 а
а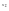
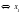
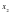
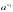
 )
)
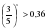
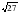
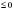
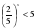
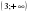
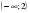

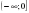
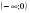
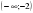
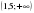
 ,
,