Государственное областное бюджетное
профессиональное образовательное учреждение
«ЛИПЕЦКИЙ ПОЛИТЕХНИЧЕСКИЙ ТЕХНИКУМ»
Методическая разработка
урока математики
на тему
«Показательная функция, её свойства и график ».
Выполнил:
преподаватель математики
первой квалификационной категории
Заварзина В.Г.
Липецк 2014 г.
Тема урока:
«Показательная функция её свойства и график».
Цели урока:
1. Образовательные:
а) обеспечить усвоение студентами знаний о показательной функции, её свойствах;
б) создать условия для развития умений получать знания посредством проведения исследовательской деятельности и анализа ситуации .
2. Развивающие:
а) развитие умений сравнивать, обобщать, правильно формулировать задачи и излагать мысли;
б) развитие памяти студентов;
в)развитие логического мышления, внимания и умения работать в проблемной ситуации.
3. Воспитательные:
а) воспитание умения работать в коллективе, взаимопомощи, культуры общения;
б) развитие познавательного интереса учащихся;
в) развитие умений преодолевать трудности при решении математических задач; воспитание таких качеств характера, как настойчивость в достижении цели;
Тип урока: изучение нового материала
Вид урока: проблемный
Методические приемы:
-самостоятельная работа (работа с раздаточным материалом);
-практический- решение задач прикладной направленности.
Межпредметные связи: физика-химия.
Оборудование и наглядные средства обучения: компьютер, классная доска, слайдовая презентация, интерактивная доска, учебник «Алгебра и начала анализа10-11» под редакцией А.Г.Мордковича, чертёжные инструменты, карточки
Методическая цель: активизировать мыслительную деятельность студентов.
Ход урока:
I.Организационный момент: подготовка студентов к уроку (проверка отсутствующих на уроке, наличие тетрадей, проверка готовности рабочих мест студентов и преподавателя, готовности учащихся к работе.)
На первом этапе преподаватель приветствует студентов, проверяет готовность группы к работе.
II Актуализация знаний обучающихся
Игра «Кто быстрее» Эта игра проводится с целью актуализации знаний студентов на уроке изучения нового материала по теме «Показательная функция, её свойства и график».
Студенту предлагается в течение 60 секунд отвечать на вопросы. (листочки розданы заранее)
Звание «самого эрудированного на уроке» присваивается тому, кто ответил на большее количество вопросов. (итог в конце урока).
Вопросы:
(в скобочках ответы студентов)
Независимая переменная (х)
Наглядный способ задания функции (графический)
График четной функции симметричен относительно чего (Оу)
График квадратичной функции называется (парабола)
Что обозначают буквой D (область определения)
Способ задания функции с помощью формулы ( аналитический)
График какой функции - прямая (линейной)
О какой функции речь? Чем больше х, тем больше у. (возрастающая)
Свойство функции f(-x) = f(x ) (четность)
Множество значений, принимаемых независимой переменной
(область определения)
11) Что обозначают буквой Е ? (область значений)
12) График нечетной функции симметричен относительно чего
(начала координат)
13) О чем речь? Чем меньше х, тем больше у. (убывание)
14) Множество целых чисел - какая буква? (Z)
15) Точки пересечения графики функции с осью Ох (нули функции)
16) Множество действительных чисел –какая буква? (R)
17) Свойство функции f(-x) = - f(x) (нечетность)
Проверка ответов
III. Изучение новой темы.
а) определение
Преподаватель. Вам предстоит сегодня много рассуждать, делать выводы, спорить.
(Мотивация для изучения новой темы.)
В жизни мы часто сталкиваемся с зависимостями между величин. Оценка по контрольной работе зависит от количества и правильности выполненных заданий, стоимость покупки от количества купленного товара и цен. Одни зависимости носят случайный характер, другие постоянны.
Давайте рассмотрим следующие законы.
Рост древесины происходит по закону A=A0*akt
A- изменение количества древесины во времени;
A0- начальное количество древесины;
t-время, к, а- некоторые постоянные.
Давление воздуха убывает с высотой по закону:P=P0*a-kh
P- давление на высоте h,
P0 - давление на уровне моря,
а- некоторая постоянная.
Изменение количества бактерий N=5t
N-число колоний бактерий в момент времени t
t- время размножения
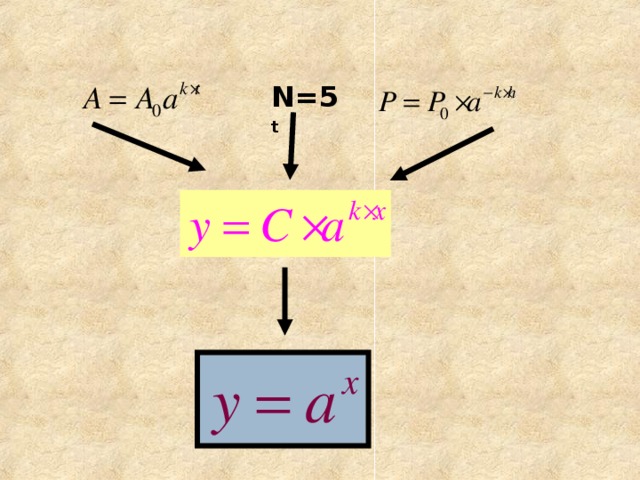
-Что общее объединяет эти процессы? -схожесть вида формулы, задающей закон у=с·акх
Тема нашего урока показательная функция, её свойства и график.
-Положим в этих формулах с=1,к=1, какую функцию получим? - у=ах
постройте график
что это за функция?
б) практическая работа.
1 вариант 2 вариант
- построить графики функций
у=2х, у=(1/2)х
на отрезке[-2;3] с шагом 1.
Проверим правильность ваших построений
Давайте сравним графики функций у=2х , у=(3/2)х , у=(5/2)х
–какие выводы мы можем сделать ? - Чем больше основание ,тем более пологий график.
А теперь сравним графики функций у=(1/2)х , у=(4/6)х, у=(1/3)х и сделаем соответствующие выводы. - Чем больше основание, тем более пологий график.
Такие функции называются показательными.
И сегодня на уроке, мы должны дать определение показательной функции, рассмотреть некоторые свойства и научится применять эти свойства при выполнении заданий, определенного вида.
Итак, попробуйте сформулировать определение показательной функции.
(студенты отвечают)
По предложенной схеме исследовать функцию. Каждый вариант исследует свою функцию
1. Область определения функции.
2. Область значений функции.
3. Точки пересечения с осями координат.
4.Промежутки возрастания и убывания.
в) проверка результатов практической работы.
Ученики делают записи в тетрадях.
IV. Закрепление изученного.
Я предлагаю вам выполнить некоторые задания по теме нашего урока.
а) Устно.
1.«Выбери показательную функцию».
а)Функции заранее записаны на доске
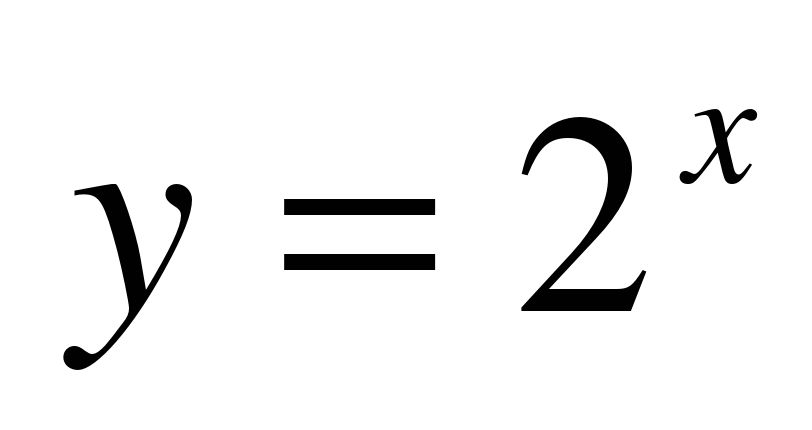 ;
; 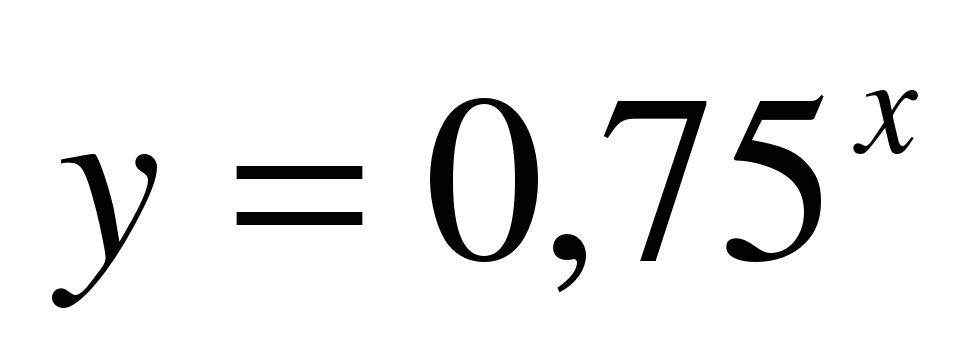 ;
; 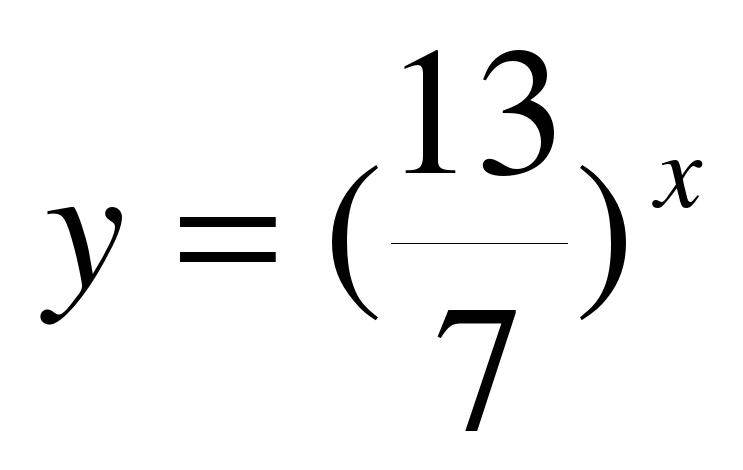 ;
; 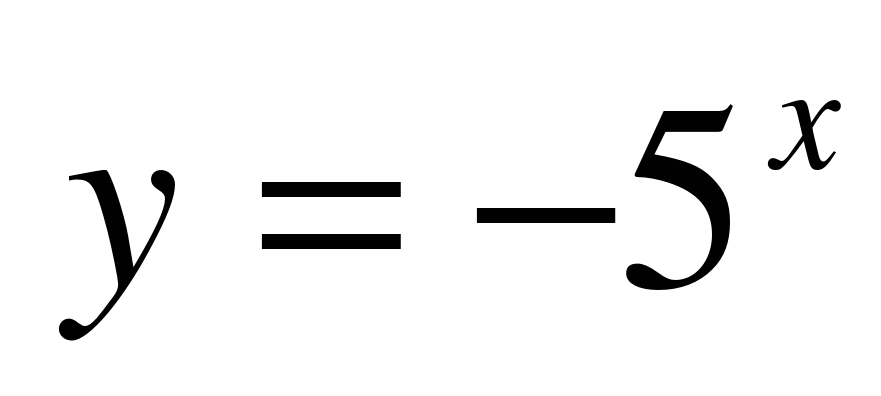 ;
; 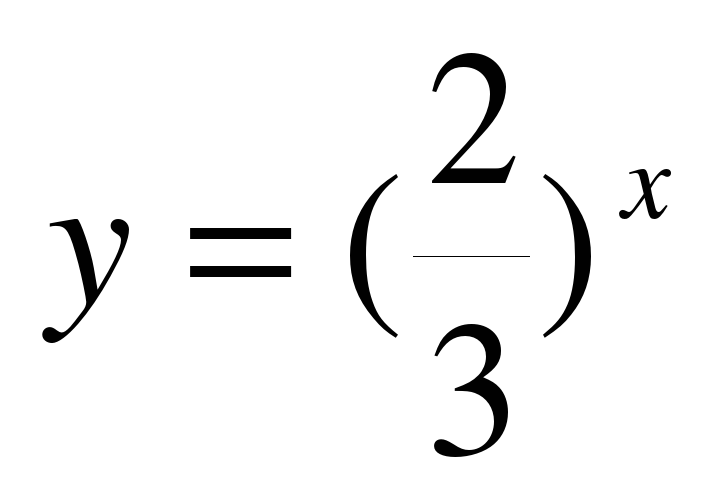 ;
; 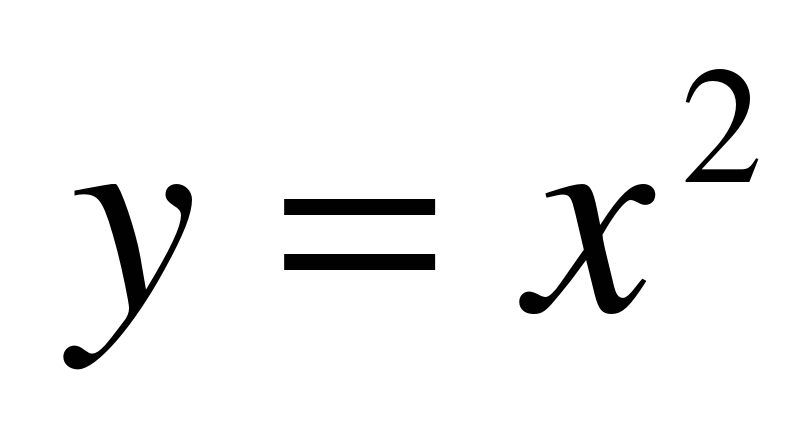 ;
; 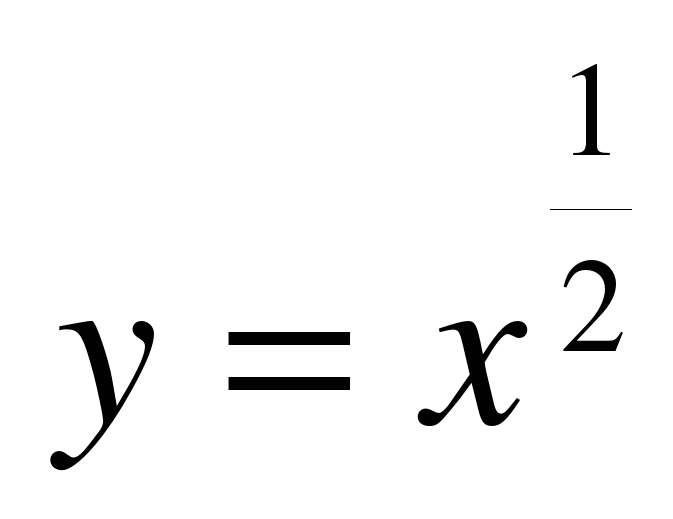 ;
; 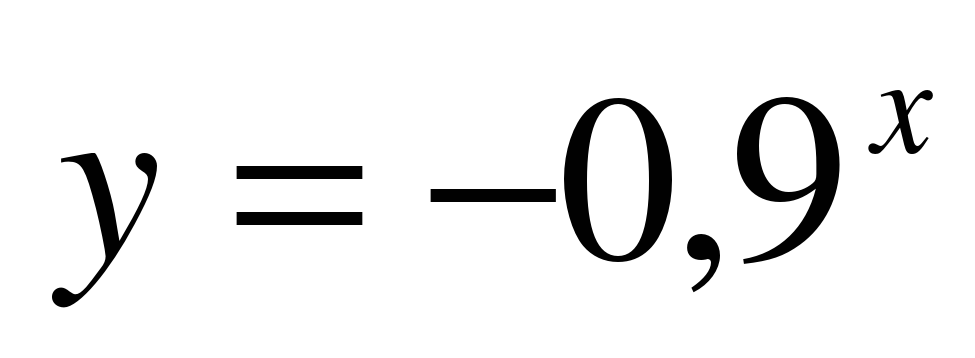 ;
; 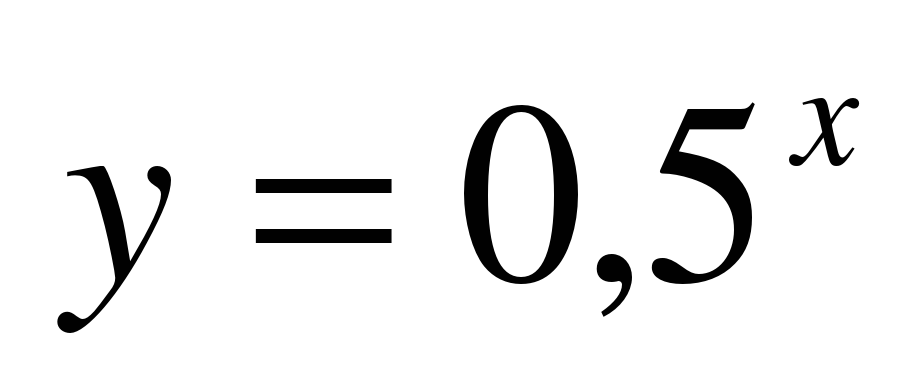 ;
; 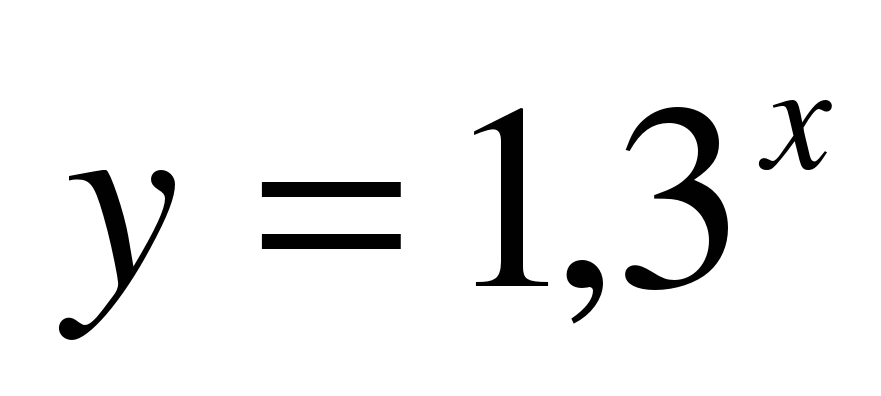 .
.
б). Из предложенного списка функций, выбрать ту функцию,
которая является показательной:
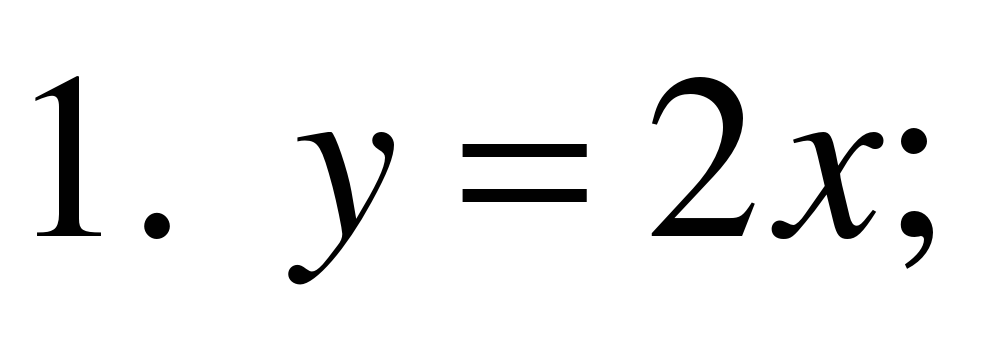
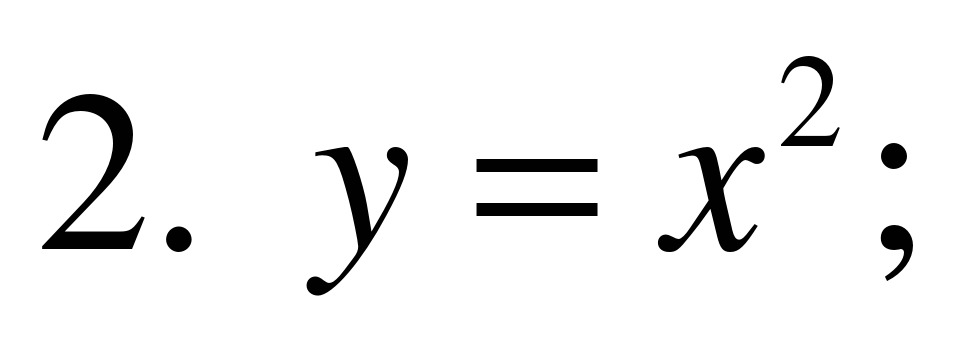
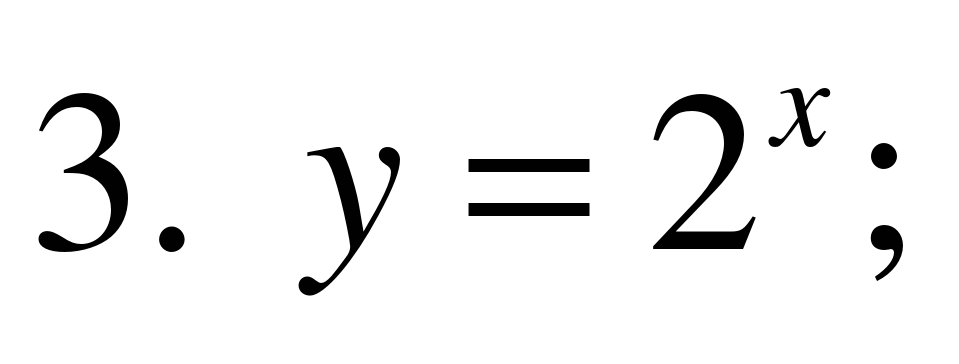
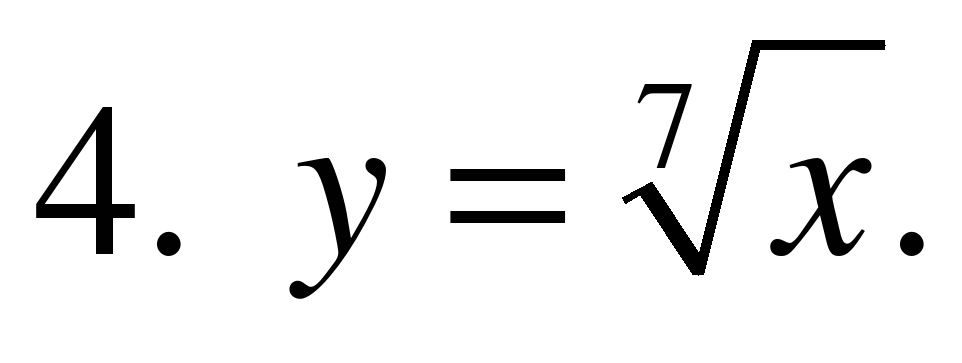
Укажите множество значений функции:
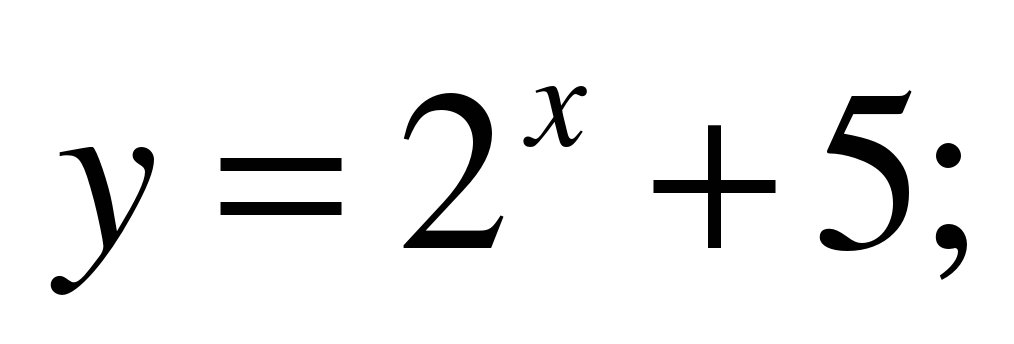
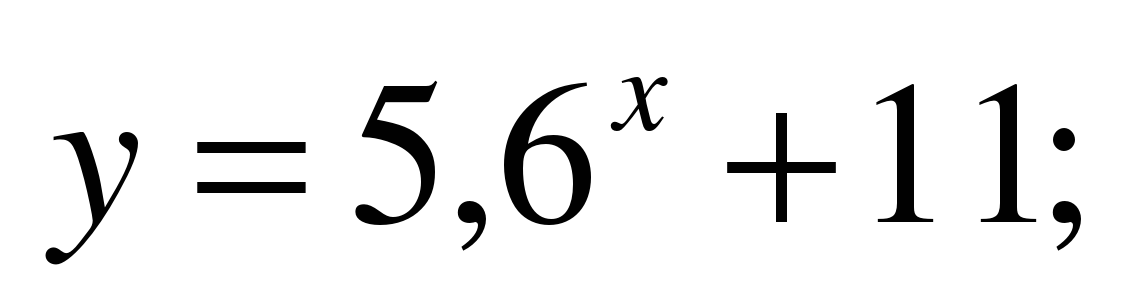
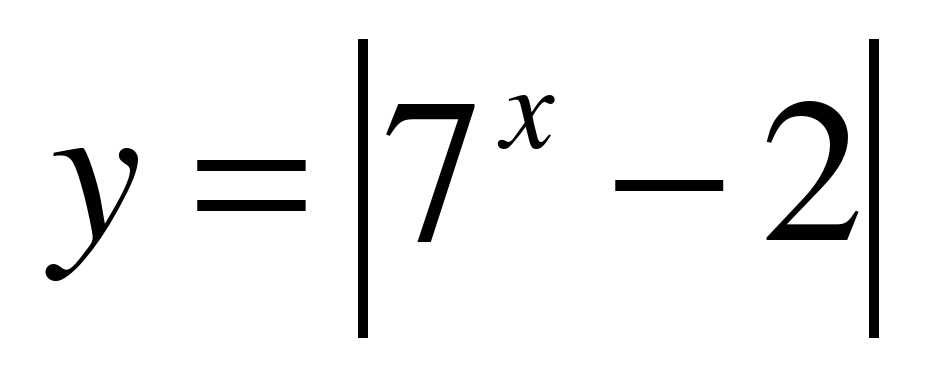
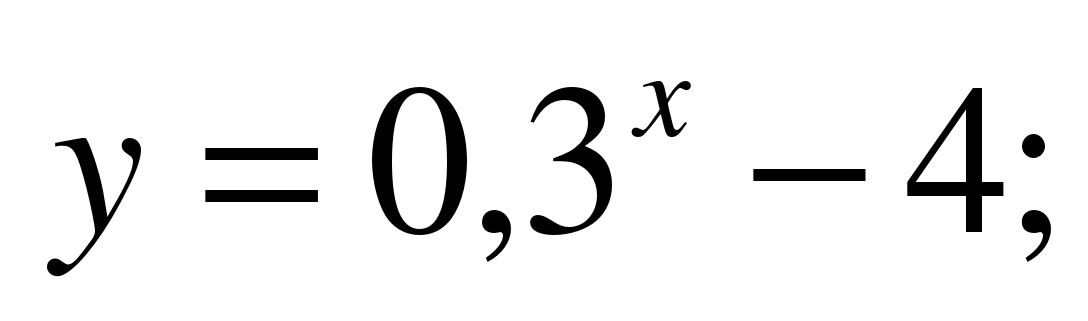
Последняя функция –решение в тетрадь
3.Дана функция: у =аx ± b. Вывести правило, по которому можно,
не выполняя построение графика данной функции,
найти область значения функции. (правило записать в тетрадь)
Вывод:
Если у = а х+ b, то Е (у) = (b; +∞)
Если у = ах -b, то Е (у) = (-b; +∞)
4. Укажите возрастающую функцию.
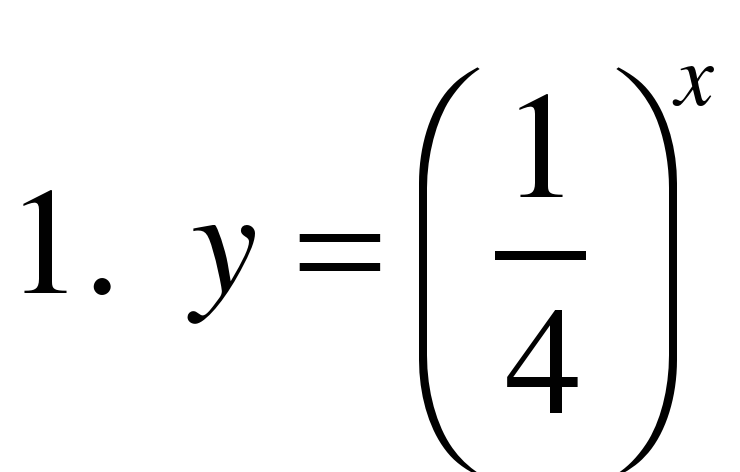
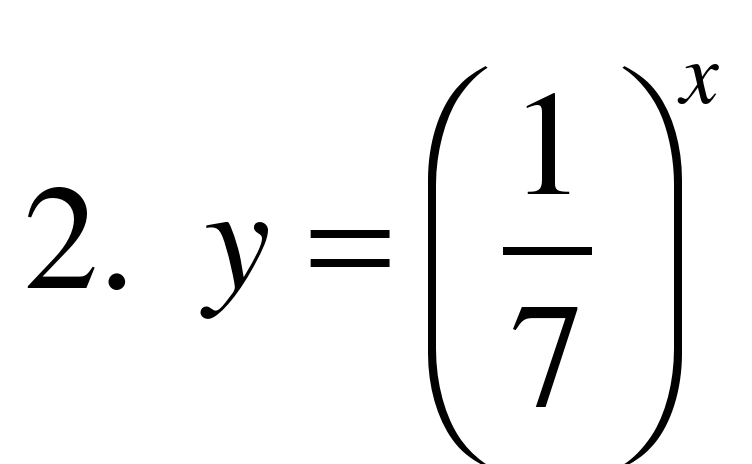
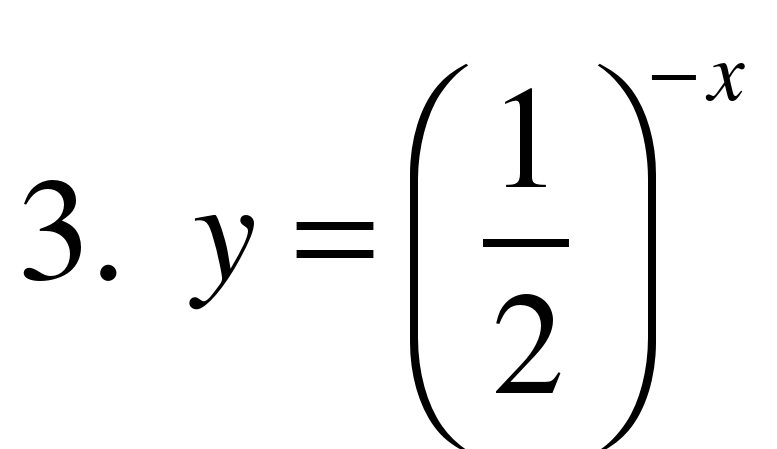
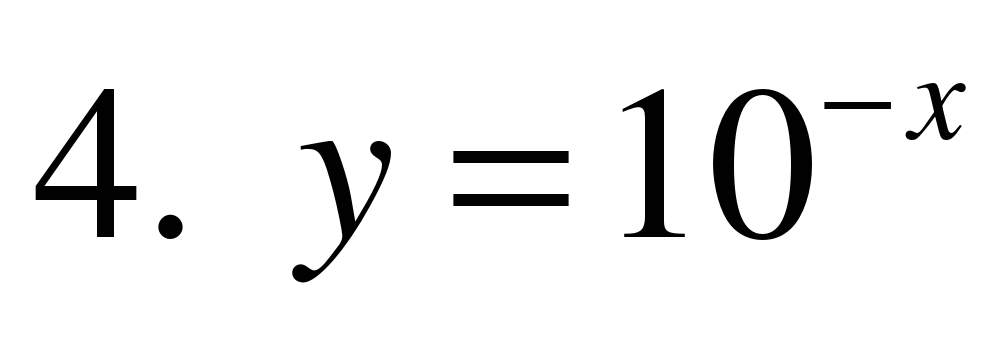
5. Укажите убывающую функцию.
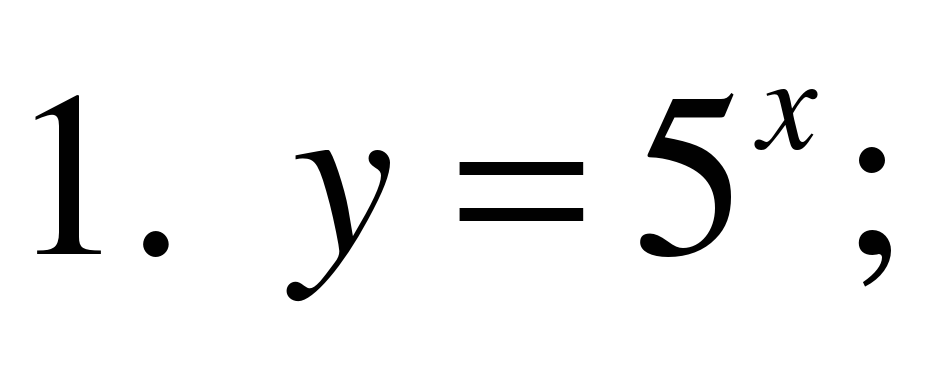
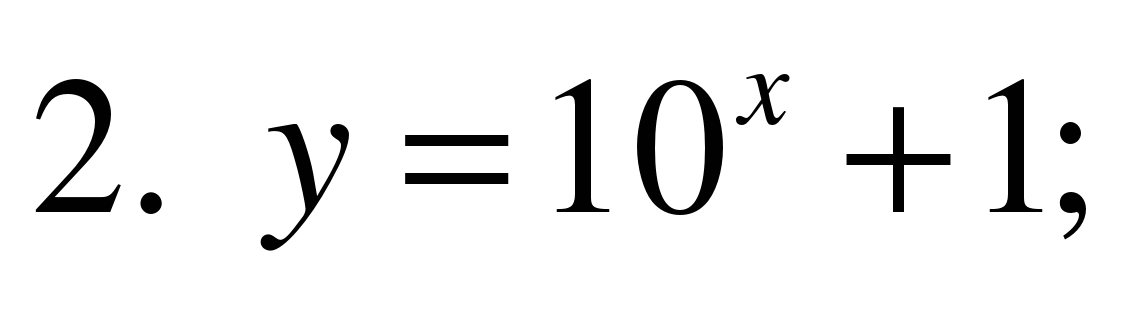
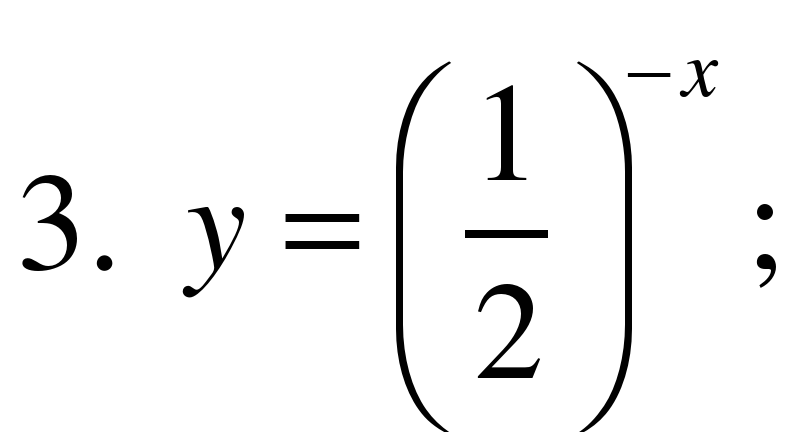
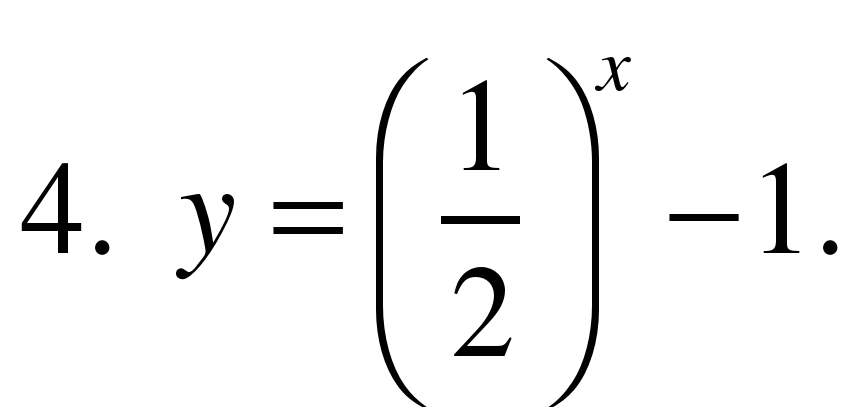
5. (Для исследования функции на монотонность).
б)) Самостоятельная работа (если необходимо с помощью учителя).
Сделайте заключение относительно основания a, если:

Дидактический материал к уроку по теме «Показательная функция»
| | Вариант №1 | Ответы | | | Вариант №2 | Ответы |
| 1. | 9,80 | 1 | 1. | 3-2 | 1/9 |
| 2. | аx 1 при а… ,х…. | а 1,х 0 или 0а1,х0 | 2. | Убывает ли y = 8 – x ? | да |
| 3. | 
| 5 | 3. | Область определения
y = x2 + 5 | Любое число |
| 4. | Множество значений x, для которых определены значения y(x), называются… | Область определения | 4. | 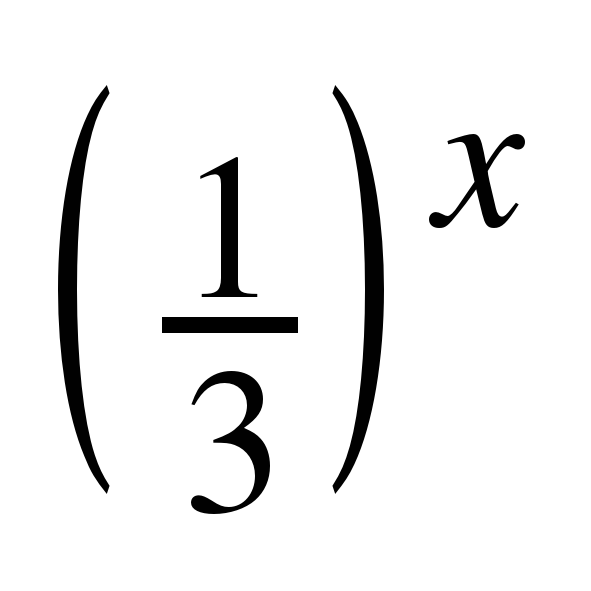 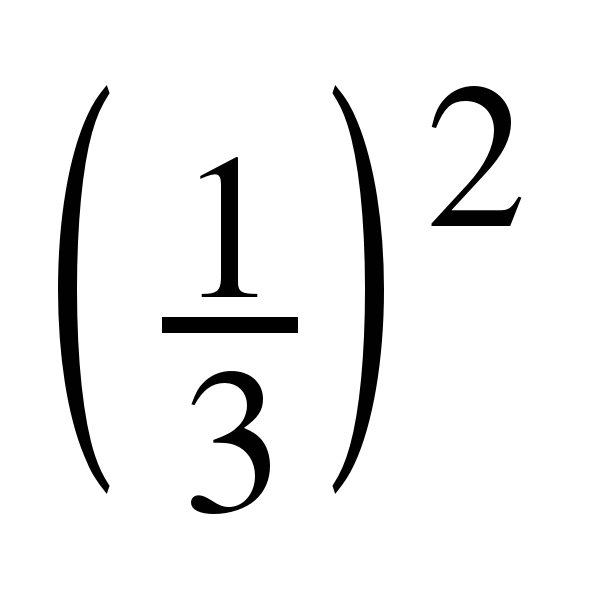 х-? | х |
| 5. | Область определения показательной функции | R | 5. | Через какую точку обязательно пройдёт график y = аx? | (0,1) |
| 6. | Область определения y = 2x+3 | Любое число | 6. | Множество значений показательной функции | E(аx)= R+ |
| 7. | Множество значений y = √х | у≥0 | 7. | а 1, а x1 а x2 Сравните x1 и x2 | x1 x2 |
| 8. | 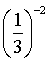
| 9 | 8. | 63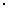 6 – 2 6 – 2 | 6 |
| 9. | Решите неравенство 3x4 | х 4 | 9. | Сравнить числа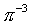 и 1 и 1 | 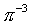 1 1
|
| 10. | Множество значений показательной функции | E(аx)= R+ | 10. | Область определения y = 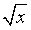 | х≥0 |
| 11. | 3x = 1, x = … | 0 | 11. | 19960 | 1 |
| 12. | y = аx . при а 1 функция … | возрастает | 12. | Название точки пересечения
y = аx с осью Оx | Ноль функции, Не пересекает |
| 13. | В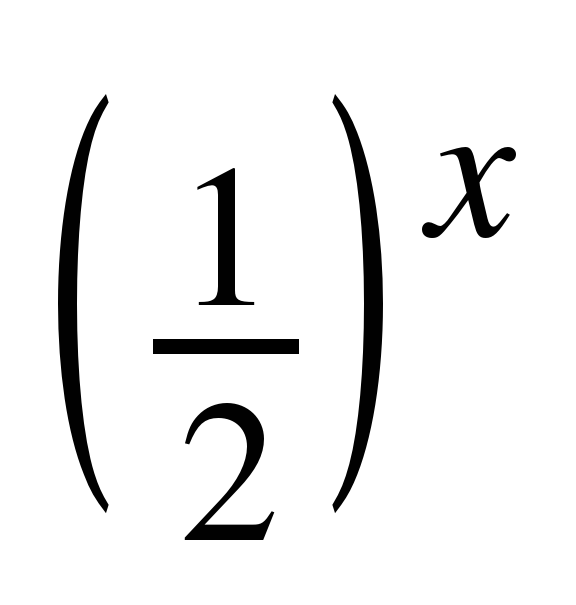 озрастает ли озрастает ли
y = ? | нет | 13. | Возрастает ли
y = 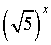 ? ? | да |
| 14. | 152 | 225 | 14. | 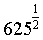
| 25 |
V. Домашнее задание.(§11 № 11.4, 11.6)
VI. Подведение итогов. Выставление оценок .
Ребята, давайте вспомним, что нового мы узнали сегодня на уроке?
Фрагменты этого урока можно также использовать при повторении пройденного материала, при подготовке к экзамену.
К уроку есть презентация.
Пояснительная записка.
Урок относится к разделу математики «Показательная и логарифмическая функции». Он является первым уроком в разделе.
Данная методическая разработка - план проведения урока математики на 2 курсе рассчитанный на 45 минут. Учитывая современную тенденцию к информатизации образовательного процесса, отдельные части урока могут быть проведены с использованием оборудования:
Данный урок является уроком изучения нового материала и направлен на решение следующих задач: а) повторение знаний, умений и навыков обучающихся необходимых для изучения новой темы; б) обеспечить усвоение учащимися знаний о показательной функции, её свойствах.
К разработке прилагается компьютерная презентация, которая сопутствует всем этапам, предусмотренным планом занятия.
Работа обучающихся в целом дает возможность коллективного творчества, проявления инициативы, развивает логическое мышление, внимание и умение работать в проблемной ситуации.
Задачи с использованием знаний о показательной функции занимают большое значение в математике. С такими задачами в наше время приходится иметь дело представителям самых разных специальностей.
Список литературы:
1. Дидактические материалы по алгебре и началам анализа для 11 класса /Б.М. Ивлев, С.М. Саакян, С.И. Шварцбурд. – М.: Просвещение, 2003.
2. Алгебра и начала анализа: Учеб. для 10–11 кл. общеобразовательных учреждений / А.Н. Колмогоров, А.М. Абрамов, Ю.П. Дудницын и др.; Под. ред. А.Н. Колмогорова. – М.: Просвещение, 2004.
3. Алгебра и начала математического анализа. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных . учреждений (профильный уровень)/А.Г. Мордкович и др. ; под редакцией А.Г. Мордковича—7-е изд., стер.—М.: Мнемозина, 2010.
4. Задачи по алгебре и началам анализа: Пособие для учащихся 10–11 кл. общеобразоват. учреждений /С.М. Саакян, А.М. Гольдман, Д.В. Денисов. – М.: Просвещение, 2003.
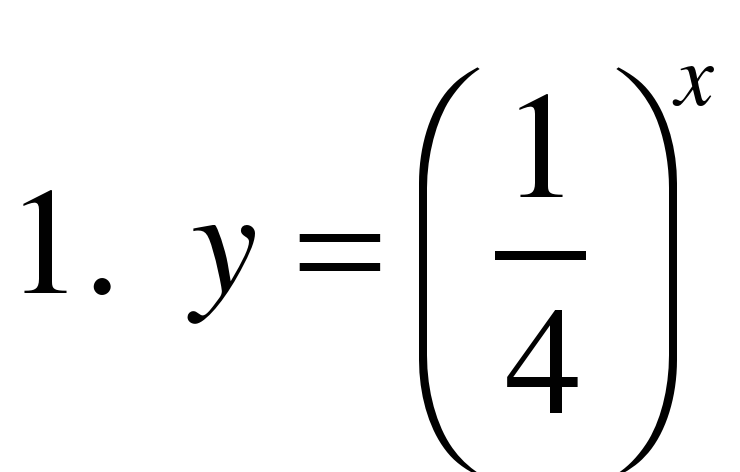
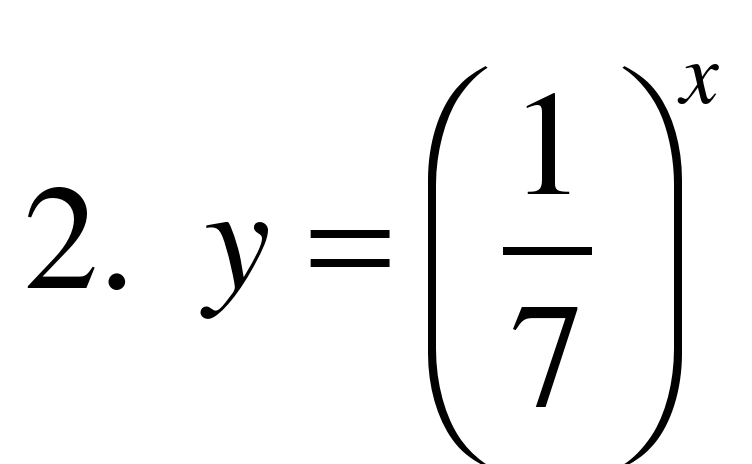




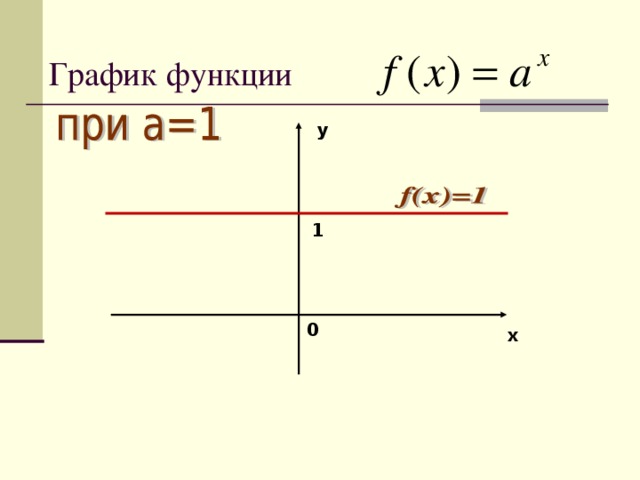



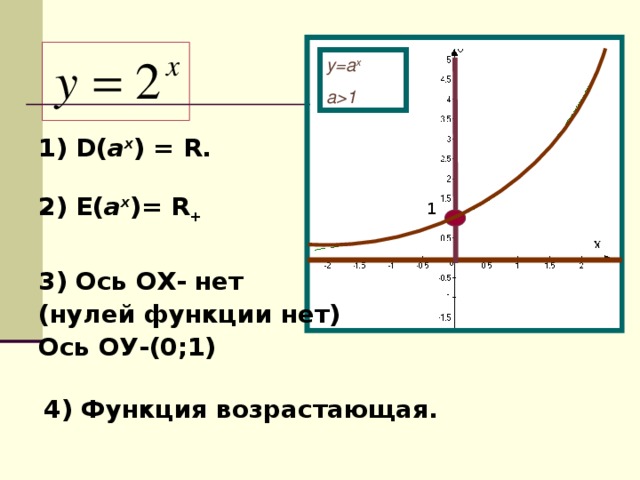 1 1) D( а x ) = R . 2) E( а x )= R + 1 3) Ось ОХ- нет (нулей функции нет) Ось ОУ-(0;1) 4) Функция возрастающая." width="640"
1 1) D( а x ) = R . 2) E( а x )= R + 1 3) Ось ОХ- нет (нулей функции нет) Ось ОУ-(0;1) 4) Функция возрастающая." width="640"
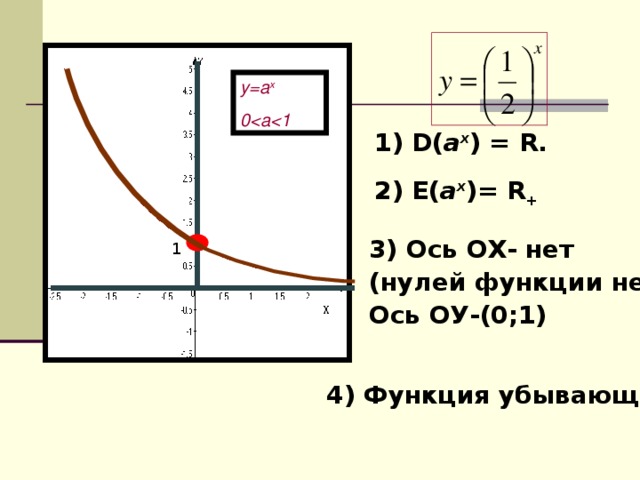
 0, для всех х 0,3 х -4 0-4 у -4 Ответ: (-4;+ ∞)" width="640"
0, для всех х 0,3 х -4 0-4 у -4 Ответ: (-4;+ ∞)" width="640"


















