Метапредметный урок по теме: "Цилиндр: площадь поверхности и объем"

МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ РОСТОВСКОЙ ОБЛАСТИ

ГБПОУ РО «ГУКОВСКИЙ СТРОИТЕЛЬНЫЙ ТЕХНИКУМ»

МЕТАПРЕДМЕТНЫЙ урок по дисциплине:

«мАТЕМАТИКА: АЛГЕБРА И НАЧАЛА АНАЛИЗА; ГЕОМЕТРИЯ»

для специальности среднего профессионального образования

19.02.10 Технология продукции общественного питания

ТЕМА УРОКА: «ЦИЛИНДР: ПЛОЩАДЬ ПОВЕРХНОСТИ И ОБЪЕМ»

рАЗРАБОТАЛА ПРЕПОДАВАТЕЛЬ:

ПИНГИНА ТАТЬЯНА ПЕТРОВНА

2017

Тема урока: Цилиндр: площадь поверхности и объем.

Цели:

Обучающая:

Изучить формулы для вычисления площади полной поверхности и объема цилиндра. Закрепить знания решением практических задач.

Развивающая:

Способствовать развитию логического мышления, пространственного воображения.

Способствовать расширению кругозора.

Воспитывающая:

Формирование интереса к предмету.

Воспитание активности, самостоятельности,

Повышение общекультурного уровня студентов.

Формируемые метапредметные умения:

- умение самостоятельно определять цели деятельности; использовать все возможные ресурсы для достижения поставленных целей;

- умение продуктивно общаться и взаимодействовать в процессе совместной деятельности, учитывать позиции других участников деятельности;

- владение навыками познавательной деятельности, способность и готовность к самостоятельному поиску методов решения практических задач;

- готовность и способность к самостоятельной информационно-познавательной деятельности, включая умение ориентироваться в различных источниках информации;

- владение навыками познавательной рефлексии, как осознания совершаемых действий и мыслительных процессов;

- целеустремленность в поисках и принятии решений, сообразительность и интуиция, развитость пространственных представлений.

Тип: Комбинированный урок.

Вид: практикум по решению задач.

Методы: проблемно-эвристический

Материально-техническое оснащение:

Презентация, сопровождающая урок; страница рабочей тетради; модель цилиндра;

Видеоролики; Учебник: Атанасян Л.С. Геометрия 10-11

Задания и методические указания для внеаудиторной работы

Ход урока

1. Организационный момент. Мотивация. Постановка цели урока.

Мы продолжаем с вами изучать тела в пространстве, и сегодня мы посвятим урок цилиндру – одному из самых распространенных тел вращения.

А вы согласны, что цилиндрическая форма очень часто встречается?

Какие кондитерские приспособления, продукты, кулинарные шедевры имеют форму цилиндра? (ответы обучающихся)

Давайте посмотрим на экран. Все что вы сейчас видите, непосредственно относится к вашей будущей специальности, и в то же время, с точки зрения математики, это все – цилиндры. (слайд)

Наверное, самое любимое блюдо многих из вас – это торт. Но вам в жизни придется не только кушать его, но и готовить. Немаловажную роль при этом имеет красивое оформление готового продукта. А так как большинство тортов имеют форму цилиндра, то знания, полученные сегодня на уроке, должны очень пригодиться для творческих личностей, какими я вас и вижу.

(слайд)

Посмотрите еще раз на тему урока. (слайд)

Как вы думаете, чему мы с вами должны сегодня научиться?

(применять знания на вычисление площади и объема при решении практических задач)

Чтобы применять знания, что мы должны узнать нового?

(Формулы для вычисления площади и объема)

Чтобы записать формулы, мы должны…(повторить, что мы знаем о цилиндре и его элементах, формулы, связанные с этими элементами (будем называть их опорными).

Значит, сначала мы должны вспомнить….(элементы цилиндра, опорные формулы)

Запишем это в тетради.

Затем узнать…(Формулы для вычисления площади и объема)

И, наконец, научиться…(применять знания на вычисление площади и объема)

Итак, кто может четко сформулировать цель урока?

- Вспомнить элементы цилиндра, опорные формулы.

- Узнать формулы для вычисления площади и объема цилиндра.

- Научиться применять знания на вычисление площади и объема цилиндра при решении практических задач. (слайд)

2. Актуализация опорных знаний.

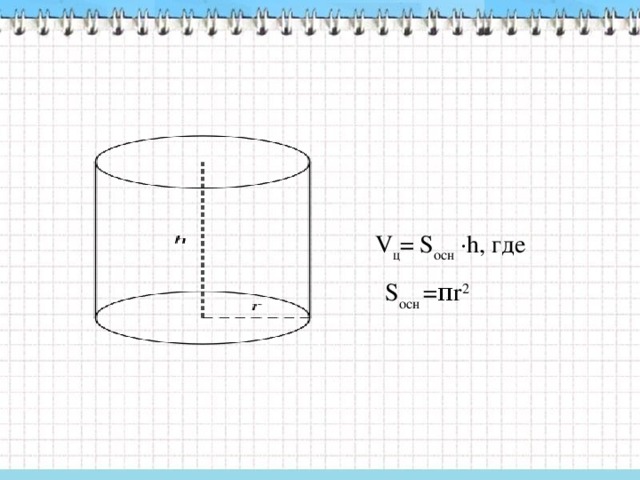
Вспомним элементы цилиндра, опорные формулы:

а) Работа с моделью (устно)

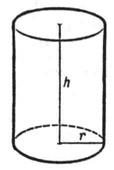
Какие элементы цилиндра вы можете назвать и показать?

- Основания верхнее и нижнее

- Боковая поверхность (цилиндрическая)

- Образующая (высота)

- Ось (высота)

б) Работа на странице рабочей тетради.

(Подписать элементы цилиндра, соответствующие стрелкам)

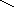Основание

Боковая (цилиндрическая) поверхность

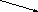
Образующая (высота)

Ось (высота)

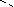
Основание

Проверьте, верно ли вы записали (слайд)

Кроме этого, нам сегодня понадобятся следующие формулы:

1. Площадь прямоугольника :_______________

   

2. Площадь круга :________________

3. Длина окружности: _________________

Микровывод: Итак, мы с вами повторили элементы цилиндра, а также вспомнили некоторые формулы из школьного курса, которые нам понадобятся в дальнейшем.

Выполнили ли мы первую цель урока? Да.

1. Сообщение – усвоение новых знаний.

Недавно, я увидела необычное оформление торта.

Такой десерт всегда будет вызывать восторг за праздничным столом!

Посмотрим фрагмент: кружево из шоколада или https://www.youtube.com/watch?v=pUi9VKXw5wM

Как видите, для такого оформления необходимо сделать определенные заготовки. А так как мы не можем сейчас сказать, какой величины у вас получится торт, то мы с вами рассчитаем площадь покрываемой поверхности в общем виде.

(Беседа сопровождается записями в тетради)

Итак, что представляет площадь боковой поверхности торта в развертке? (прямоугольник)

Как определить площадь прямоугольника? (длину умножить на ширину)

Что является шириной? (высота торта)

Что является длиной? (длина окружности)

Вспомним (или посмотрим в тетради) формулу длины окружности

Итак, площадь боковой поверхности цилиндра равна S_бок =2πr∙h

Что представляет собой верх торта? (круг)

Чтобы сделать заготовку для украшения торта, надо знать… (площадь круга) S_осн =πr²

Как мы можем вычислить радиус? (измерить диаметр и разделить его на 2)

Итак, общая площадь оформляемой поверхности равна S=S_осн+ S_бок =πr²+2πr∙h=πr(r+2h)

Вначале урока я говорила, что считаю вас творческими людьми, поэтому не исключаю, что вы установите торт таким образом, что у вас будет возможность украсить и нижнее основание. Тогда площадь оформляемой поверхности будет равна:

S=2S_осн+ S_бок=2πr²+2πr∙h=2πr(r+h)

Откройте учебник на странице 33. И сравните формулу с тем, что получилось у нас. Оказывается, выполняя это задание, мы не просто узнали формулу для вычисления площади полной поверхности, а доказали ее!

Давайте сделаем чертеж и запишем формулы в тетради.

Обратите внимание, нужно всегда контролировать: одно или два основания учитываются при решении конкретной задачи и применять соответствующую формулу. Также не обязательно использовать общую формулу, можно отдельно вычислить площадь основания (если их два, то умножить на 2), площадь боковой поверхности и сложить.

Тех, кого заинтересовало такое оформление, вы можете найти множество идей, задав в поисковой системе: украшение торта шоколадным кружевом.

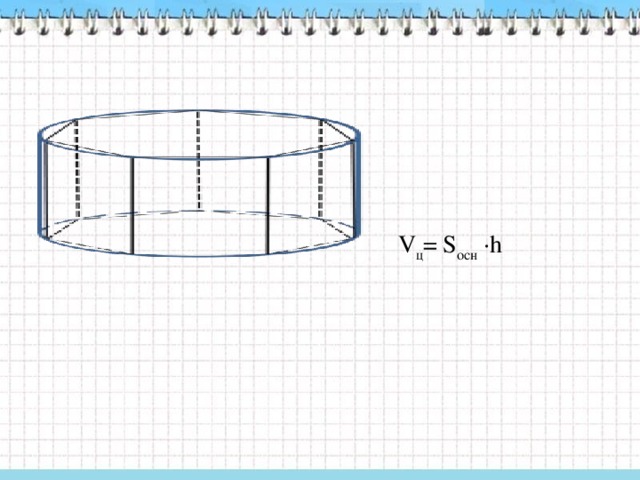
У нас осталось незаполненной одна строка: объем цилиндра.

Чтобы понять, какова формула для вычисления объема цилиндра, представим себе, что при обрезке торта у нас получился не круг, а многоугольник с очень маленькими сторонами. Тогда данное тело у нас не цилиндр, а… (прямая призма)

Чему равен объем призмы? Откройте таблицу из внеаудиторной работы и посмотрите. Эту часть вы должны были уже заполнить. V_пр=S_осн ∙h

В курсе геометрии доказывается, что V_ц= V_пр=S_осн ∙h

Микровывод: Итак, мы с вами выполнили еще одну цель урока: узнали формулы для вычисления площади и объема цилиндра.

4. Закрепление изученного материала и выработка умений и навыков

Посмотрим еще один фрагмент видео: Зеркальная глазурь

https://www.youtube.com/watch?v=rWIqMxslJ-w

А теперь посмотрите на условие в тетради. Эта задача имеет дифференцированный подход: если вы выполняете только первое задание, то получаете оценку за этот вид работы «3». Для выполнения второго задания нужно пространственное воображение и знания предыдущих уроков (объем параллелепипеда). Вместе первое и второе задание оцениваются на «4». Для выполнения третьей задачи вы должны мыслить логически и самостоятельно найти метод решения. Возможно, вам поможет сообразительность и интуиция. Работа парами. Этот вид работы должен занять 20 минут

«на 3»

Вычислить площадь, которую нужно покрыть глазурью, если торт имеет диаметр 24 см и высоту 10 см. При расчетах π=3,14

Решение Так как диаметр равен 24, то r=12 см h=10 см

S=S_осн+ S_бок S_осн =πr²=3,14∙12²=452,16 см² S_бок =2πr∙h=2∙3,14∙12∙10=753,6 см²

S=452,16+7563,6=1205,76 см²

(ход решения может быть другим)

«на 4»

Какой объем глазури (в см³) нужно приготовить, если толщина слоя равна 2 мм.

Решение 2 мм=0,2 см

Верх торта – круг, толщина слоя – высота. Верхняя покрываемая часть - цилиндр

Объем верхней части: V=S_осн ∙h S_осн =πr²=452,16 см² h=0,2 см V=452,16 ∙0,2=90,432 см³

Боковая часть – прямоугольник, толщина слоя – высота. Боковая покрываемая часть – параллелепипед (или четырехугольная призма)

Объем боковой части: V=S_бок ∙h S_бок =2πr∙h=753,6 см² h=0,2 см V=753,6∙0,2=150,72 см³

Объем всей покрываемой поверхности глазурью: V=90,432+150,72=241,152 см³

(ход решения может быть другим)

«на 5»

Можно ли готовить глазурь в кастрюльке, объемом 1 л ?

Подсказка: 1 л =1 дм³

1 дм = 10 см

Решение Т.к. 1 дм=10 см, то 1 см=0,1 дм 1 см³=0,001 дм³

V=241,152 см³=241,152∙0,001=0,241152 дм³≈0,241 л

Вывод: объем глазури, равный 0,241 л (примерно 1 стакан) можно готовить в кастрюле, объемом 1 л.

(ход рассуждений может быть другим)

5. Диагностика прочного усвоения знаний, умений и навыков. Выставлением поурочного балла.

Проанализируем задачу и посмотрим, научились ли вы применять полученные знания.

(анализ на слайде)

Полностью выполнили задачу верно… и, учитывая активность на уроке, … получают за урок «отлично».

Справились с двумя задачами и показали умение общаться и взаимодействовать в процессе совместной деятельности …., за урок они получают «хорошо»

Целеустремленность проявили …, они заслуживают оценку «удовлетворительно»

А наш урок подходит к концу и мы должны подвести итоги.

Какие цели мы ставили перед собой? (слайд)

Выполнили мы поставленные цели?

6. Инструктаж по выполнению домашнего задания.

Обратите внимание на домашнее задание, записанное у вас в рабочей тетради:

1. Продолжите заполнение таблицы из внеаудиторной работы, новыми формулами, изученными сегодня.

2. Украшение тортов настолько разнообразно, что мы не в силах охватить все на уроке. Например, сейчас очень модно оформлять торт мастикой. Предлагаю составить и решить задачу на вычисление площади и объема при украшении торта мастикой. Рекомендую виртуально приготовить нестандартный торт: большого размера или многоярусный.

3. При желании, ролики о украшении тортов, которые мы сегодня с вами смотрели, можно полностью посмотреть на:

1) https://www.youtube.com/watch?v=rWIqMxslJ-w

2) https://www.youtube.com/watch?v=pUi9VKXw5wM

7. Рефлексия

Прежде чем мы закончим урок, я хотела бы, чтобы вы заполнили последние строки вашей рабочей тетради:

После изучения темы «Цилиндр. Площадь поверхности и объем»:

• Я узнал(а)____________________________________________

• Мне на уроке понравилось______________________________

• Меня удивило, что_____________________________________

• В дальнейшем я _______________________________________

При наличии времени, озвучить и обсудить.

Спасибо за урок!

11

Тема урока: Цилиндр: площадь поверхности и объем.

Цель:1) Вспомнить_________________________________________________.

2) Узнать_____________________________________________________.

3) Научиться__________________________________________________.

1. Запишите элементы цилиндра, указанные стрелками:

_____________

_____________

_____________

_____________

__________

Опорные формулы:

1. Площадь прямоугольника :_______________

   

2. Площадь круга :________________

3. Длина окружности: _________________

2. Формулы для вычисления

площади полной поверхности и объема цилиндра:

Площадь боковой поверхности цилиндра:­­________

Площадь основания цилиндра: ________

Площадь полной поверхности цилиндра:

____________________________________________

Объем цилиндра: _______________

(чертеж)

3. Решите задачи:

«на 3»

Вычислить площадь, которую нужно покрыть глазурью, если торт имеет диаметр 24 см и высоту 10 см. При расчетах π=3,14

«на 4» ^{рабочая тетрадь}

Какой объем глазури ( в см³) нужно приготовить, если толщина слоя равна 2 мм.

«на 5»

Можно ли готовить глазурь в кастрюльке, объемом 1 л ?

Подсказка: 1 л =1 дм³

1 дм = 10 см

4. Домашнее задание

1) Заполните соответствующую строку таблицы внеаудиторной работы (Цилиндр. Площадь поверхности и объем)

Таблица находится в заданиях и методических указаниях:

Тема 8 Многогранники и круглые тела

2) Составьте и решите задачу на оформление торта мастикой.

Все необходимые данные найдите в сети Интернет.

3) При желании, ролики о украшении тортов, можно полностью посмотреть на :

1) https://www.youtube.com/watch?v=rWIqMxslJ-w

2) https://www.youtube.com/watch?v=pUi9VKXw5wM

5. Рефлексия

Закончите предложение:

После изучения темы «Цилиндр: площадь поверхности и объем»:

• Я узнал(а)____________________________________________

• Мне на уроке понравилось______________________________

• Меня удивило, что_____________________________________

• В дальнейшем я _______________________________________

Тема урока : Цилиндр: площадь поверхности и объем.

Творить  – значит не копировать или подражать.

Кулинария – это язык, с помощью которого можно передать гармонию, счастье, красоту, сложность, поэзию, волшебство, юмор, провокацию, культуру – в общем, все, из чего складывается наша жизнь.

А математика ей в этом помогает…

Тема урока : Цилиндр: площадь поверхности и объем.

Цели урока:

• Вспомнить элементы цилиндра,

опорные формулы.

• Узнать формулы для вычисления площади и объема цилиндра.
• Научиться применять знания на вычисление площади и объема цилиндра при решении практических задач.

Площадь круга : S= πr 2

Длина окружности: C=2 πr

Площадь прямоугольника : S=ab

кружево из шоколада

S осн =πr 2

h

C=2πr∙

S бок =2πr∙h

S осн =πr 2

S=S осн + S бок =πr 2 +2πr∙h=πr(r+2h)

h

C=2πr∙

S бок =2πr∙h

S осн =πr 2

S=2S осн + S бок =2πr 2 +2πr∙h=2πr(r+h)

V ц = S осн ∙h

V ц = S осн ∙h, где

S осн =πr 2

Зеркальная глазурь

Вычислить площадь, которую нужно покрыть глазурью, если торт имеет диаметр 24 см и высоту 10 см. При расчетах π=3,14

Решение Так как диаметр равен 24, то r=12 см h=10 см

S=S осн + S бок

S осн =πr 2 =3,14∙12 2 =452,16 см 2

S бок =2πr∙h=2∙3,14∙12∙10=753,6 см 2

S=452,16+7563,6=1205,76 см 2

(ход решения может быть другим)

Какой объем глазури (в см 3 ) нужно приготовить, если толщина слоя равна 2 мм.

Решение 2 мм=0,2 см

Верх торта – круг, толщина слоя – высота. В Верхняя покрываемая часть - цилиндр

Объем верхней части: V=S осн ∙h

S осн =πr 2 =452,16 см 2 h=0,2 см

V=452,16 ∙0,2=90,432 см 3

Боковая часть – прямоугольник, толщина слоя – высота. Боковая покрываемая часть – параллелепипед (или четырехугольная призма)

Объем боковой части: V=S бок ∙h S бок =2πr∙h=753,6 см 2 h=0,2 см V=753,6∙0,2=150,72 см 3

Объем всей покрываемой поверхности глазурью: V=90,432+150,72=241,152 см 3

(ход решения может быть другим)

Можно ли готовить глазурь в кастрюльке, объемом 1 л ?

Подсказка: 1 л =1 дм 3

1 дм = 10 см

Решение Т.к. 1 дм=10 см, то 1 см=0,1 дм 1 см 3 =0,001 дм 3

V=241,152 см 3 =241,152∙0,001=0,241152 дм 3 ≈0,241 л

Вывод: объем глазури, равный 0,241 л (примерно 1 стакан) можно готовить в кастрюле, объемом 1 л.

(ход рассуждений может быть другим)

Цели урока:

• Вспомнить элементы цилиндра,

опорные формулы.

• Узнать формулы для вычисления площади и объема цилиндра.
• Научиться применять знания на вычисление площади и объема цилиндра при решении практических задач.

Спасибо за урок!