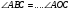Методическая разработка урока по теме "Вписанный угол"

Постановка проблемы

Добрый день, ребята.

Посмотрите на слайд, красным цветом выделены дуги окружностей, градусная мера которых известна.

Вычислите градусную меру углов, изображенных на рисунках 1-5.

Какие углы изображены?

На рисунке 5 изображен центральный угол?

Что необходимо сделать, чтобы решить поставленную задачу?

Отвечают

Узнать, что это за угол и как его измерить.

Определение темы урока

Чтобы узнать как называется данный угол и сформулировать тему урока, откройте стр 168, найдите п 73, прочитайте 1 абзац, используя чтение с пометками.

Итак, какова тема урока?

Верно, впишите тему урока в рабочий лист, с которым мы сегодня работаем.

В ваших рабочих листах напротив заданий имеется колонка для самооценки, выполняя задания на уроке, вам предстоит оценить свою работу по заданным критериям, в конце урока посчитаем количество набранных баллов и определим отметку по шкале в конце рабочего листа.

Используя памятку «Определение» и прочитав еще раз 1 абзац п 73, определите ключевые слова и сформулируйте определение вписанного угла, впишите его в рабочий лист.

Проверим, что получилось, подчеркивая ключевые слова.

Если вы верно определили ключевые слова, поставьте себе 1 балл в колонку самооценка, иначе 0 баллов

Вписанный угол

Вписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекают окружность

Применение определения

Используя определение, найдите на рисунках а-е вписанные углы, запишите в рабочие листы буквы, над которыми изображены данные углы. И начертите вписанный угол на окружности в рабочем листе. Проверяем: вписанные углы изображены под буквами а и б. поставьте себе в рабочий лист 1 балл, если задание выполнили верно, иначе 0 баллов

Задачи урока

Чтобы определить задачи урока, предлагаю поиграть в игру «Верю-не верю».

Верите ли вы, что

1. Вписанный угол измеряется дугой, на которую он опирается?

2. Вписанные углы, опирающиеся на одну и ту же дугу, равны?

3. Вписанный угол, опирающийся на полуокружность, равен 180 ⁰?

4. Задач на вписанный угол нет в открытом банке ОГЭ?

Тогда, сформулируйте задачи урока.

Формулируют задачи урока.

Теорема о вписанном угле

Приступаем к решению 1 задачи, для этого прочитайте теорему на стр 169. Запишите формулировку в рабочий лист.

Для доказательства это теоремы применим методом полной индукции: от частного к общему. Возможны три случая расположения вписанного угла и центра окружности: 1 сторона угла проходит через центр окружности, 2 центр окружности находится между сторонами угла, 3 центр окружности находится в стороне от сторон угла.

Рассмотрим доказательство первого случая вместе.

Сравните вписанный и центральный углы, опирающиеся на одну дугу.

Вписанный угол = половине центрального угла.

Сейчас вам предстоит, работая в группах, доказать 2 и 3 случаи, сведя их к 1 случаю.

Группа 1 доказывает 2 случай, группы 2,3 – 3 случай, группа 4 доказывает 2 случай, используя доказательство из учебника на стр 169. Напоминаю правила работы в группе.

Прошу группу 1 представить доказательство случая 2, группу 2 – доказательство случая 3.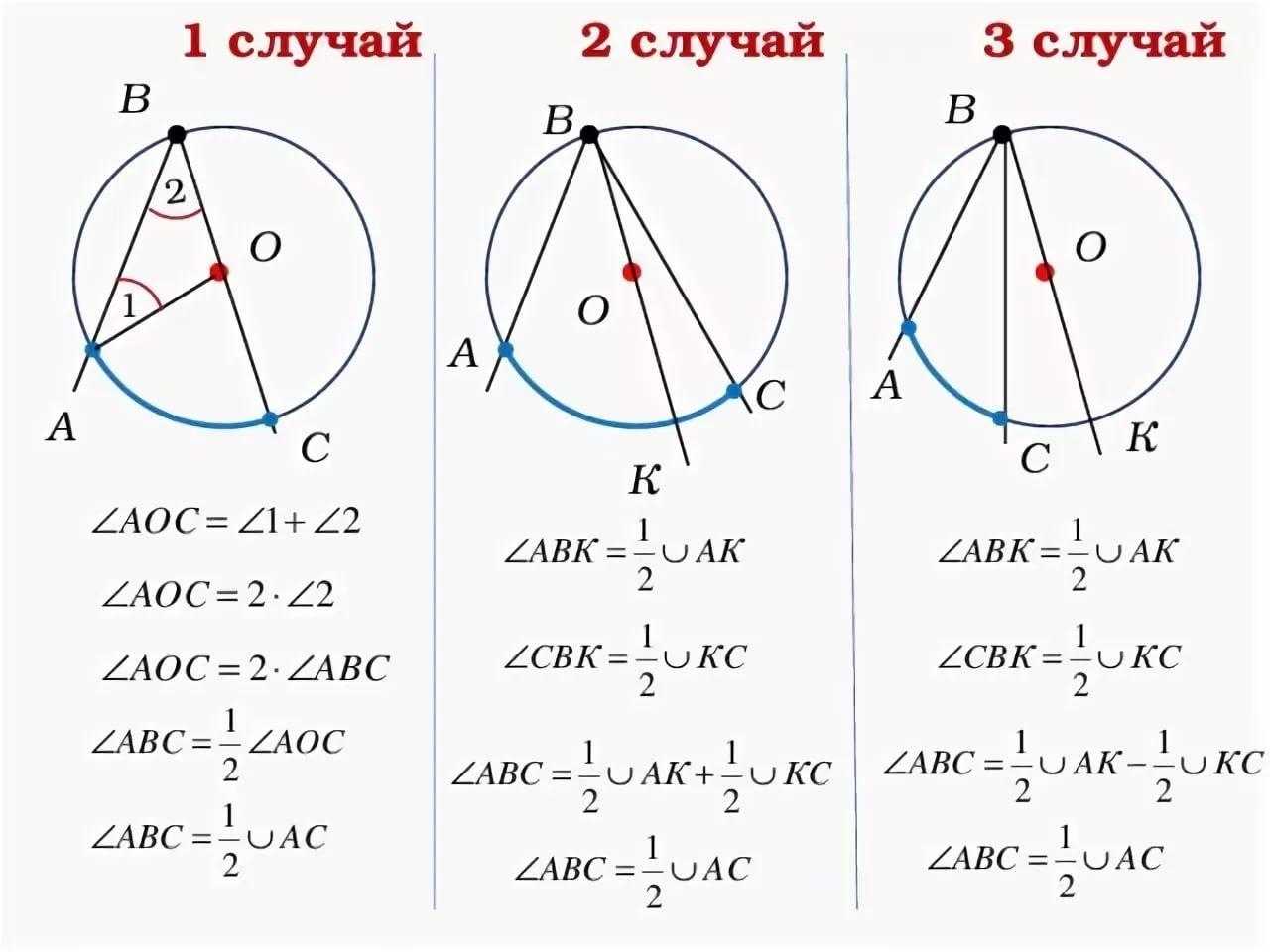

Если вы доказали часть теоремы без помощи учебника – поставьте себе 2 балла, если использовали учебник – 1 балл, если не смогли доказать теорему – 0 баллов

Применение теоремы

Используя теорему, решим устно задачу №653 под буквами а, б в паре, под в-д самостоятельно

Проверим ответы:

а – 24⁰, б- 28⁰30′, в-45⁰, г- 62⁰, д – 90⁰

если вы выполнили задание самостоятельно верно, поставьте 1 балл, иначе – 0 баллов.

Вывод сл 1 и 2

Переходим к решению 2 и 3 задачи. Выясним, равны ли вписанные углы, опирающиеся на одну и ту же дугу? Кто хочет доказать это утверждение.

Это сл 1 из теоремы, запишите его в рабочий лист.

Вписанный угол, опирающийся на полуокружность, равен 180 ⁰? Докажите это утверждение.

Сл 2 Вписанный угол, опирающийся на полуокружность, - прямой.

Решение задач

Используя теорему и сл 1 и сл 2, найдите по готовым чертежам х на рис 1-8.

Обменяйтесь рабочими листами с соседом по парте, Проверим ответы рис 1 – 40⁰, рис 2 – 164⁰, рис 3 – 30⁰, рис 4 – 130⁰, рис 5 – 90⁰, рис 6 – 120⁰, рис 7 – 75⁰, рис 8 - 60⁰.

За каждый правильный ответ поставьте 1 балл. То есть всего за выполнение этого задания вы можете набрать максимально 8 баллов.

Физминутка

Для того, чтобы решить 4 задачу попросим Викторию найти в открытом банке ОГЭ на сайте ФИПИ задачу, в которой используется вписанный угол или установить. Что таких задач в банке нет.

А мы проведем разминку. Если я буду показывать вам вписанный угол, вы выполняете приседание, если центральный - поднимаете руки вверх

Решают задачу ОГЭ

Решим задачу, которую нашла Вика в открытом банке ОГЭ на сайте ФИПИ.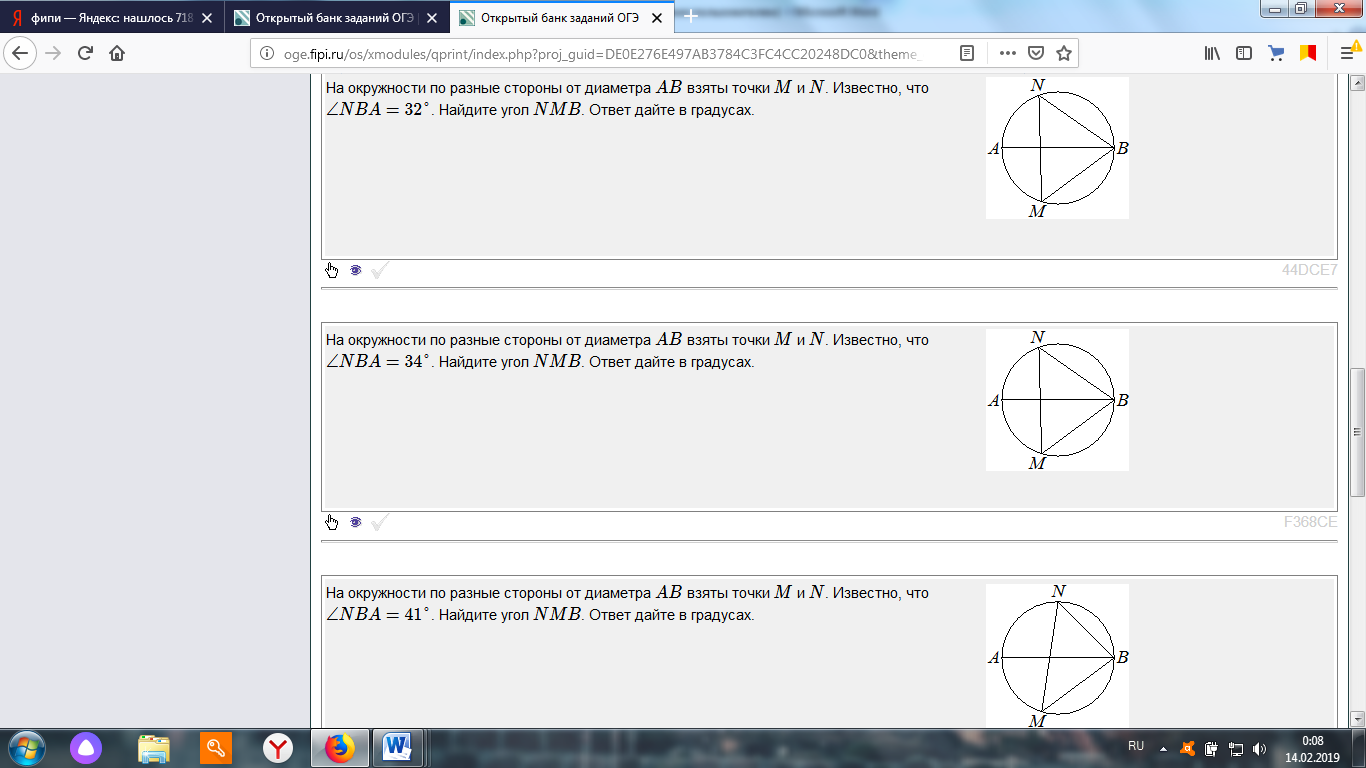

Сверим свое решение с эталоном .

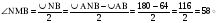
Если вы выполнили это задание верно, поставьте себе 1 балл в рабочий лист.

Делает чертеж. Решают самостоятельно

Рефлексия

Вернемся к нашей игре верю- не верю. Все ли мы распределили верно?

Можем ли сейчас решить задачу, с которой столкнулись в начале урока? Решите ее. Угол = 70⁰. Если вы справились с этой задачей, поставьте себе 1 балл

Д/З

Запишите домашнее задание. Выучить теоретический материал. № 654. Дополнительное задание: найти из открытого банка ОГЭ задачу, которую вы бы смогли решить используя теоретический материал, изученный сегодня на уроке и решите ее.

Оценивание работы

Посчитайте количество баллов в столбце самооценка и по шкале в конце рабочего листа выставите себе оценку.

С учетом ваших оценок я выставлю вам отметку за урок. Оцените свою работу на уроке: поднимите

- цель достигнута

- справляюсь, но есть ошибки

- ещё нужно над этим работать

№

Задание

Решение

Самооценка

1

Прочитав 1 абзац п 73 (стр 168), определите ключевые слова, сформулируйте определение вписанного угла.

ОПРЕДЕЛЕНИЕ:

Вписанный угол – это_______________________

__________________________________________

__________________________________________

__________________________________________

__________________________________________

2

Используя определение, найдите на рисунках а-е вписанные углы, запишите в рабочие листы буквы, над которыми изображены данные углы. Начертите свой вписанный угол.

Вписанные углы: ________________________

3

Запишите формулировку теоремы о вписанном угле в рабочий лист

Сравните вписанный и центральный углы, опирающиеся на одну дугу.

ТЕОРЕМА: _______________________________

___________________________________________

___________________________________________

___________________________________________

___________________________________________

4

Используя теорему, решите устно задачу №653 под буквами а- б

в паре, под в-д самостоятельно

В паре: а ________ б ________

Самостоятельно:

в _________г _________д _________

5

Запишите формулировку следствий из теоремы

Используя теорему и Сл 1, Сл 2, найдите по готовым чертежам х на рис 1-8.

Сл1: ______________________________________

______________________________________________________________________________________

Сл2: ______________________________________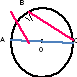

______________________________________________________________________________________

Рис 1. х=

Рис 2. х =

Рис 3. х=

Рис 4. х =

Рис 5. х=

Рис 6. х =

Рис 7. х=

Рис 8. х =

6

Решите задачу из открытого банка ОГЭ на сайте ФИПИ

Количество набранных баллов

Отметка

1-6

2

7-9

3

10-12

4

13-14

5