Логарифмдік теңдеулерді шешу.
Логарифмдік теңдеулерді төмендегі алгоритм бойынша шешеді:
Мүмкін мәндерінің жиының анықтайды: 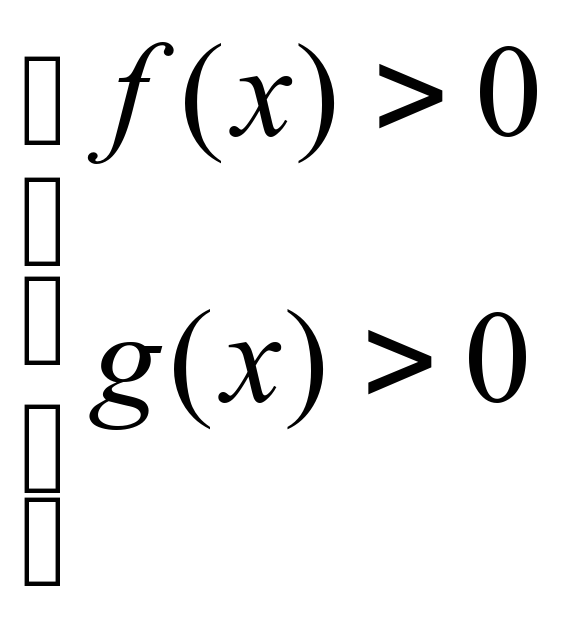
Логарифм теңдеулерді
logaf(x)=logag(x), (a1, a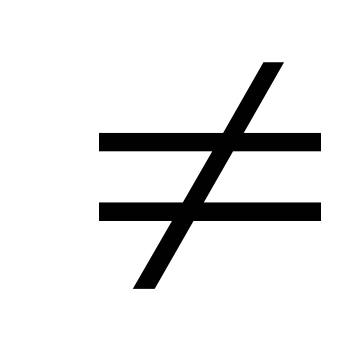 1),
1),
түріне келтіріп шешеді.
3. f(x)=g(x) теңдеулері шешіледі.
4. Теңдеудің түбірлерін ММЖ мәндерімен сәйкес анықтайды.
1-мысал,ln(x+4)+ln(2x+3)=ln(1-2x)
1. ММЖ анықталады: 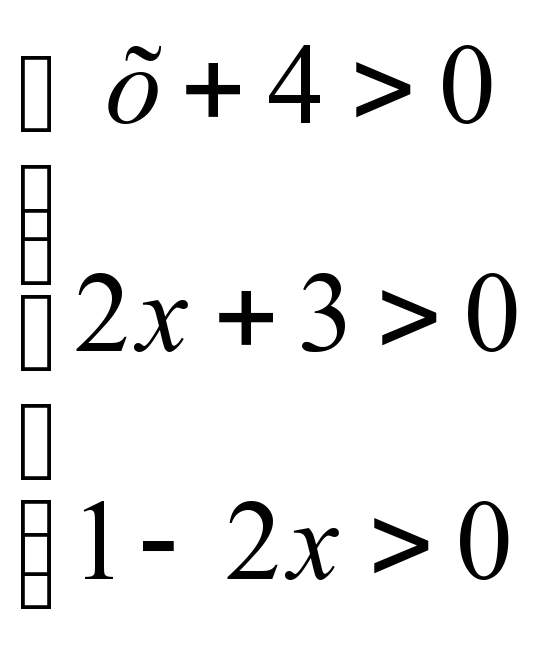 = -1.5
= -1.5
ММЖ:(-1,5;0,5)
ln(x+4)(2x+3)=ln(1-2x) =
(х+4)(2х+3) =(1-2х)
2х2+11х+12=1-2х
2х2+13х+11=0
Д=169-88=81
х1=-1; х2=-5,5
к вадраттық теңдеудің түбірлерін ММЖ (-1,5;0,5) салыстырамыз -1с(-1,5;0,5) ал 0,5с(-1,5;0,5)
вадраттық теңдеудің түбірлерін ММЖ (-1,5;0,5) салыстырамыз -1с(-1,5;0,5) ал 0,5с(-1,5;0,5)
Сонымен берілген логарифмдік теңдеудің түбірі -1.
Жауабы -1.
2-мысал.log32x- log3x-3=3
1. ММЖ-ны табамыз: x0
2. log3х-ті алмастырамыз у-айнымалысына: log3х=у
3. у2-у-3=3
4. Квадраттық теңдеуге келтіреміз: у2-у-6=0
Дискрименант табамыз: Д=12+4*1*(-6) =25
у1=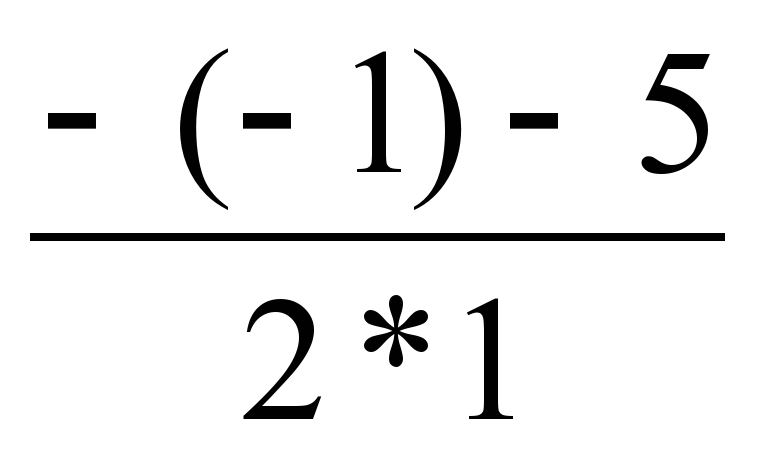 =-2 у2=
=-2 у2=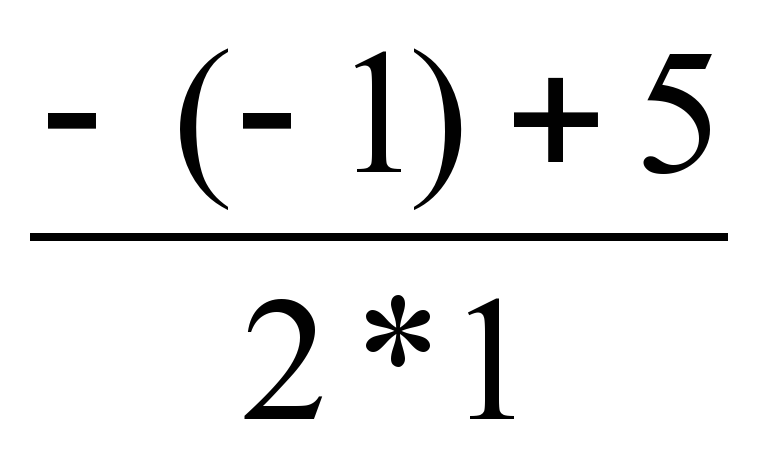 =3
=3
5. у-тердің мәндерін орнына қоямыз log3х=у
log3х=-2 log3х=3
х=3-2 х=33
х=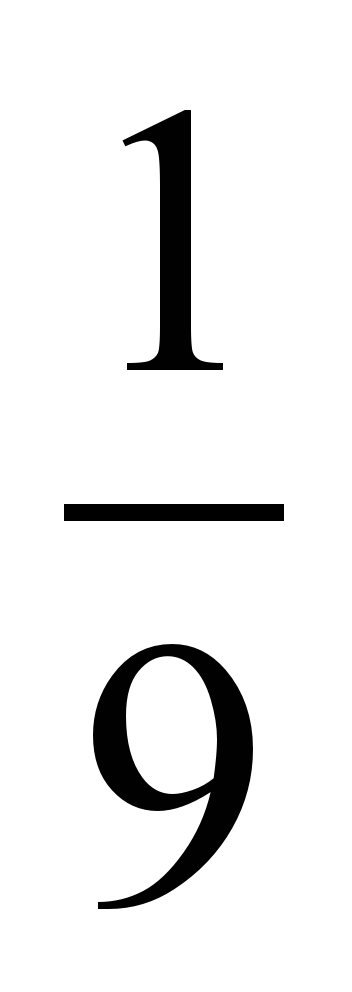 х=27
х=27
6. Жауабы:  және 27.
және 27.
Тақырыпты меңгергенінде тексеріп көр:
1)log 5(x+1)= log5(4x-5)
1. ММЖ анықтайсың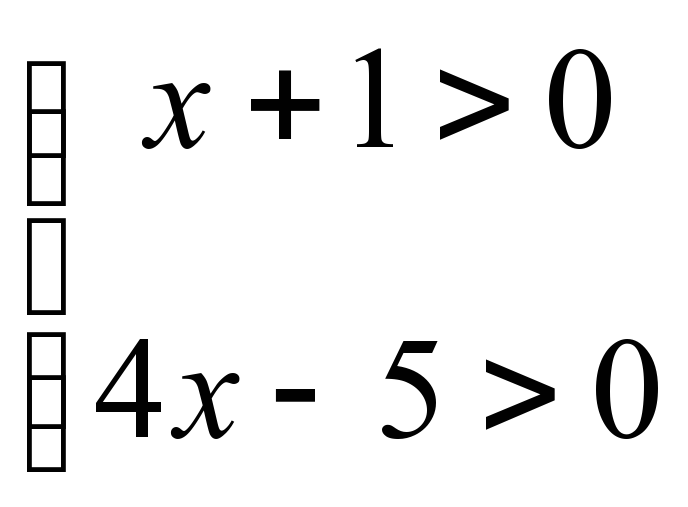 =
=
2. х+1=4х-5 теңдеуді шешіңіз
3. х-тің мәнің ММЖ-мен тексер.
Жауабы:
2) log3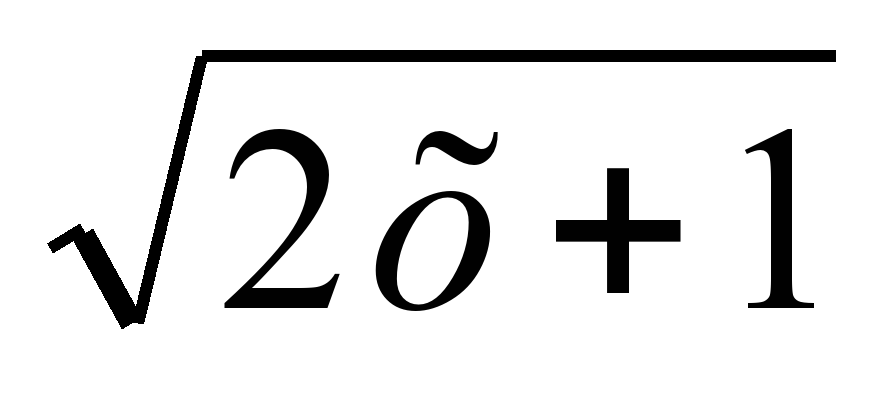 =1
=1
1. ММЖ анықтайсын: 2х+10 =
=
2. logаа =1 қасиетін пайдаланып
log3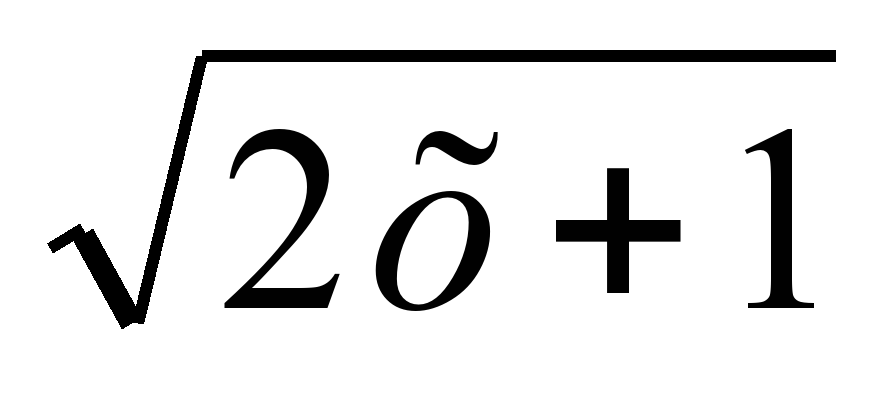 = log33
= log33
теңдеін шеш(1-ші есепке қара)
3. 3. х-тің мәнің ММЖ-мен тексер.
Жауабы:
3) 3 log82х+2 log8х+2=3
1. . ММЖ анықтайсын:
2. log8х =у алмастыру қажет( тақырыптың 2-ші мысалына қара)
3.у-тің мәндерің қойып, log8х =у теңдеілерді шешіңдер
4. . х-тің мәнің ММЖ-мен тексер.
Жауабы:
Тақырыпты меңгергенінде тексеріп көр:
1) lg(3x-2)=3-lg25
1. . ММЖ анықтайсын: 3х-2 0 =
2. логарифм қасиеті бойынша: 3= lg103 = lg(3x-2)= lg103-lg25
lg(3x-2)= lg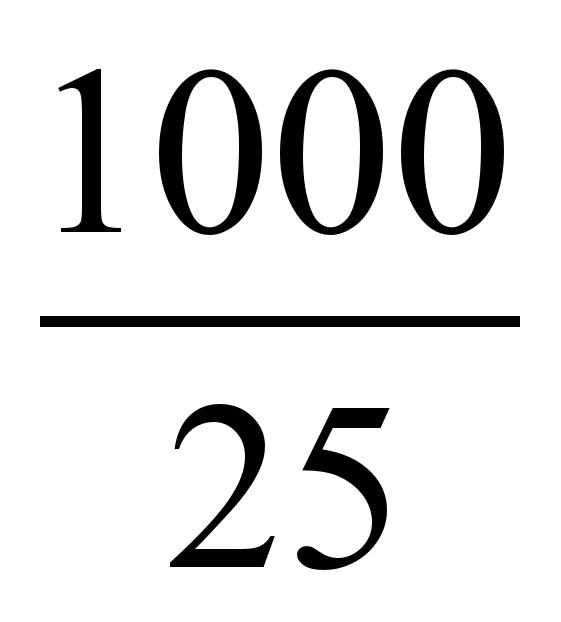
3х-2=40
Теңдеуін шеш
3. х-тің мәнің ММЖ-мен тексер.
Жауабы:
2) log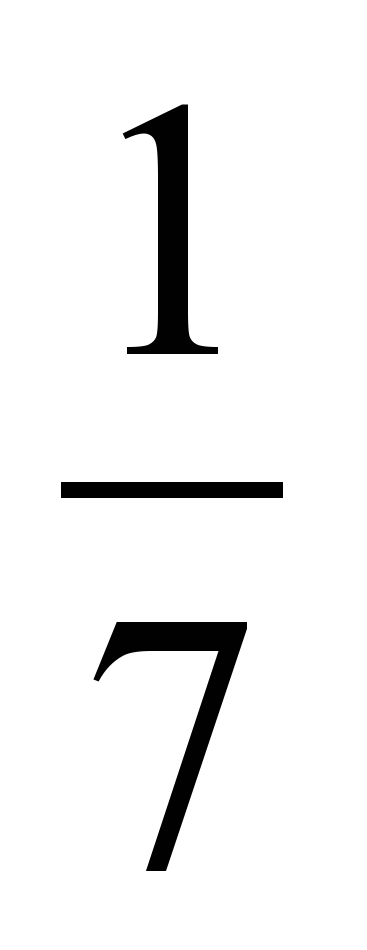 (x+5)=-1
(x+5)=-1
1. ММЖ анықтайсын х+50=
2. логарифм қасиеті бойынша -1= log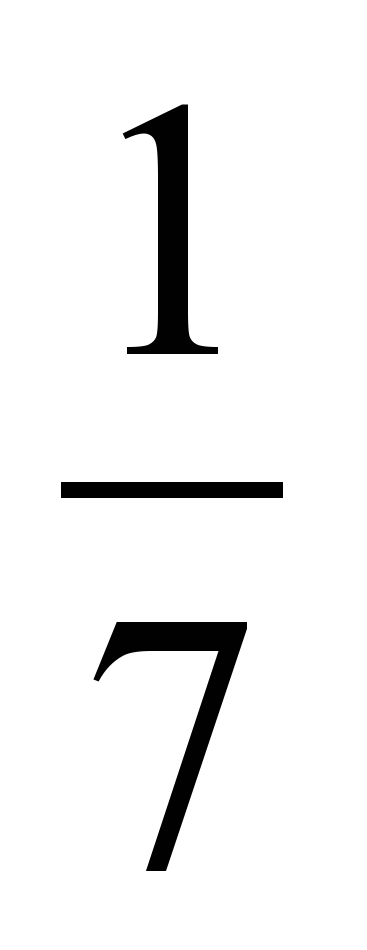 7
7
Теңдеуді шеш:
3. х-тің мәнің ММЖ-мен тексер.
Жауабы:
3) log 32 x+ log 3 х=1
1. . ММЖ анықтайсын:
2. log3х =у алмастыру қажет( тақырыптың 2-ші мысалына қара)
3.у-тің мәндерің қойып, log 3ху теңдеілерді шешіңдер
4. . х-тің мәнің ММЖ-мен тексер.
Жауабы:
Тақырыпты меңгергенінде тексеріп көр:
1)2log0.5x= log 0.5(2x2-x)
1. . ММЖ анықтайсын: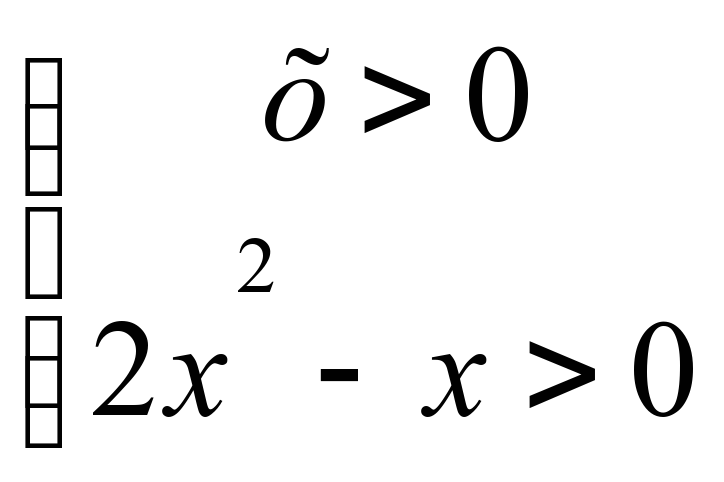 =
=
2. Логарифм қасиеттерін пайдаланып: 2log0.5x= log0.5x2
log0.5x2= log 0.5(2x2-x) теңдеуін
х2=2х2-х теңдеуіне келтіріп х-тің мәнін табыңыз.
3. х-тің мәнің ММЖ-мен тексер.
Жауабы:
2) log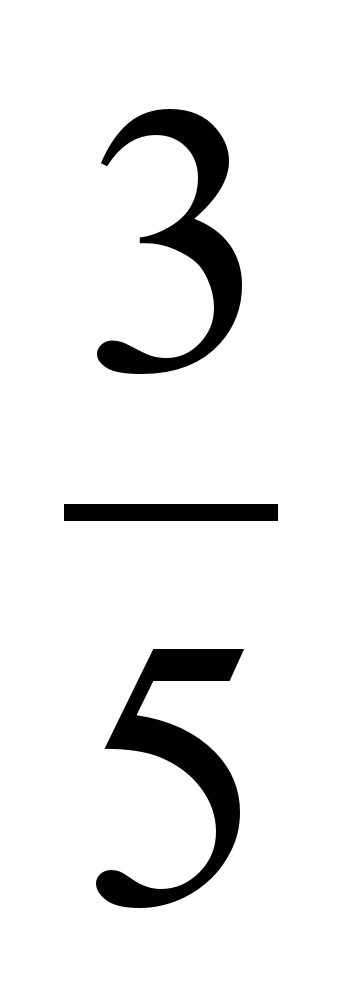
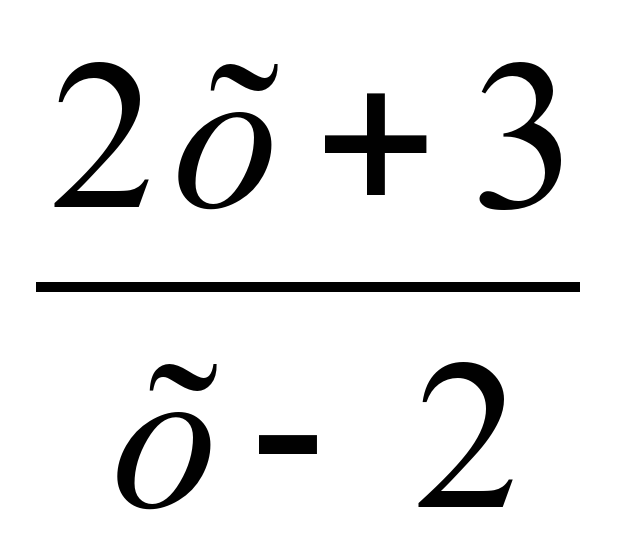 =1
=1
1. ММЖ анықтайсын 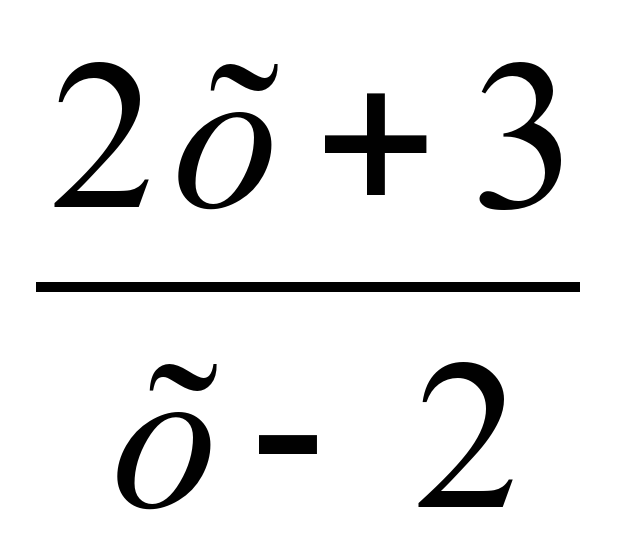 0 =
0 =
2.1= log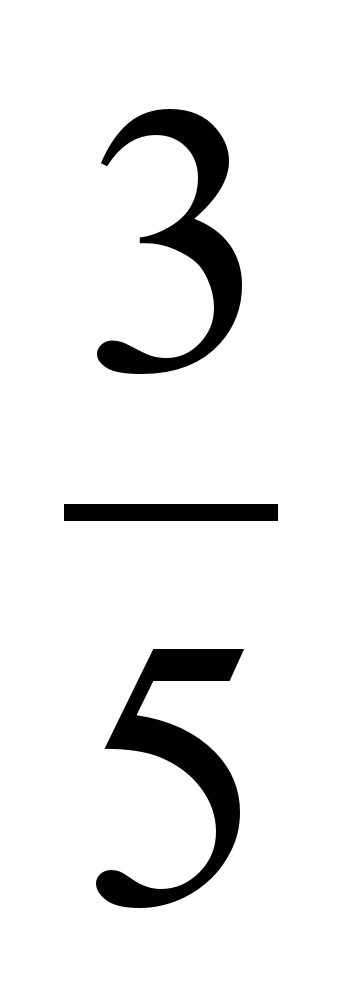
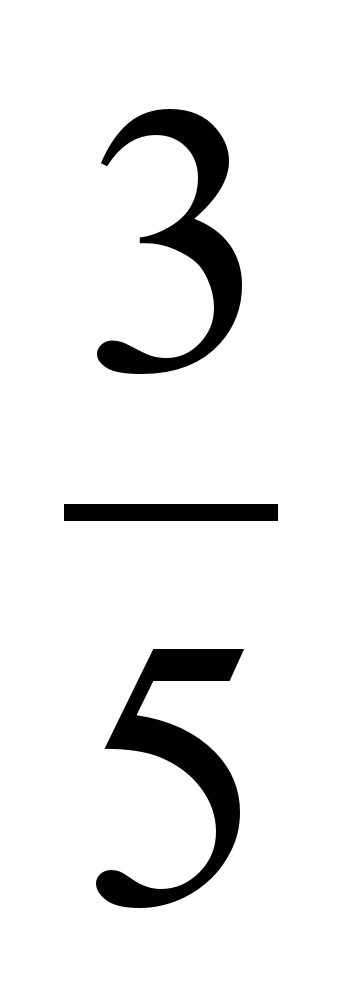 алмастырып 1-ші мысалға қарап теңдеуді шеш
алмастырып 1-ші мысалға қарап теңдеуді шеш
3. х-тің мәнің ММЖ-мен тексер.
Жауабы:
3)lg2(10x)+lg(10x)=6
1 . ММЖ анықтайсын:
1. . ММЖ анықтайсын:
2. lg10х =у алмастыру қажет( тақырыптың 2-ші мысалына қара)
3.у-тің мәндерің қойып, lg10х =у теңдеілерді шешіңдер
4. . х-тің мәнің ММЖ-мен тексер.
Жауабы:
Тақырыпты меңгергенінде тексеріп көр:
1) log5(x-10)=2+log52
1 . ММЖ анықтайсын: х-10 0 =
2. Логарифмнің қасиеттерін пайдаланып 2 = log552 = log525 алмастыр
және log525+ log52 = log525*2 = log550 теңдігін пайдаланып теңдеуді шеш:
log5(x-10)= log550
х-10 =50
3 х-тің мәнің ММЖ-мен тексер.
Жауабы
2) log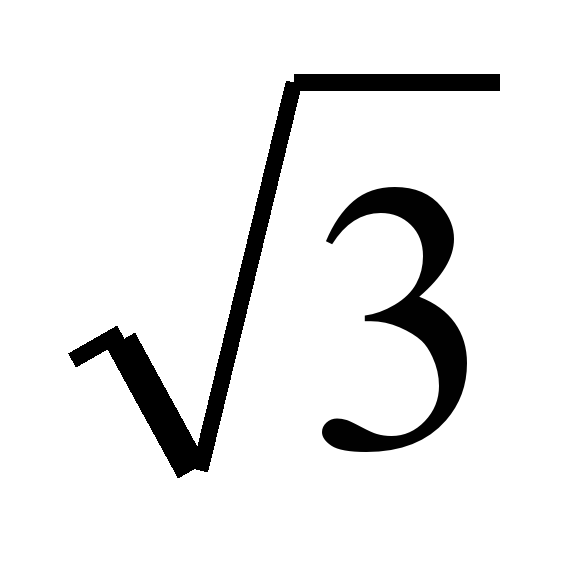
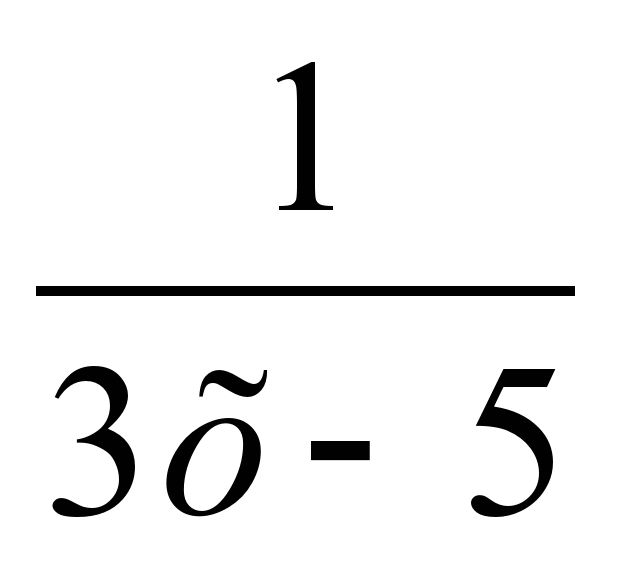 =0
=0
1. ММЖ анықтайсын: 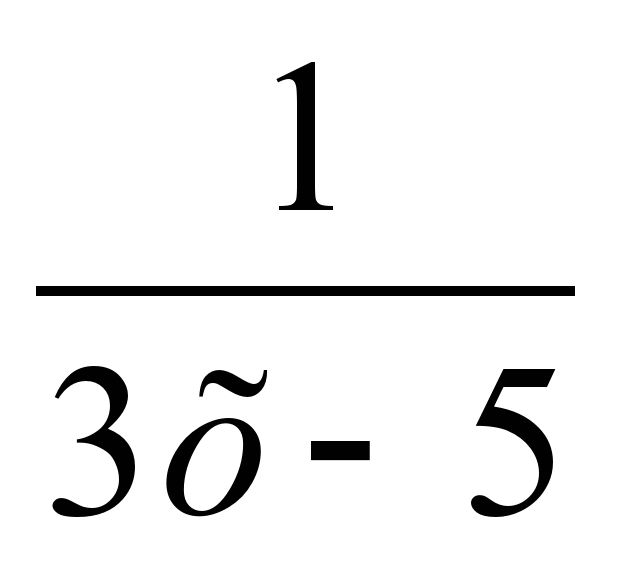 0 =
0 =
2. Логарифмнің қасиеттерін пайдаланып 0= log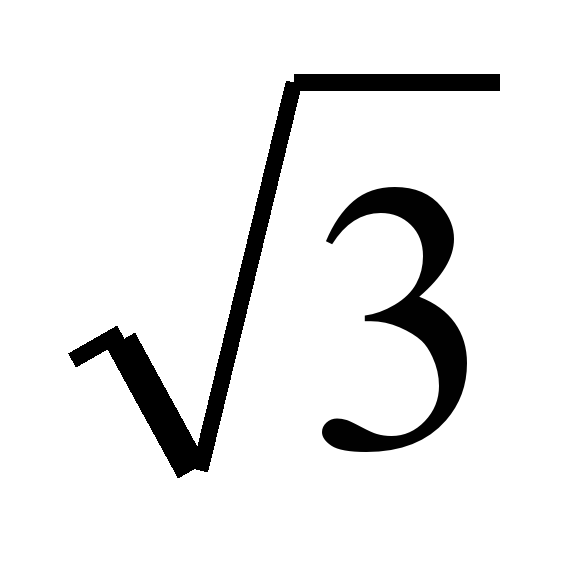 1 теңдігін пайланып:
1 теңдігін пайланып:
log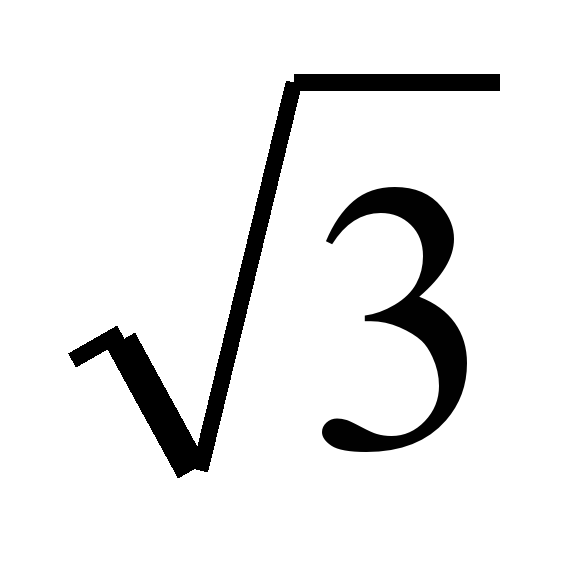
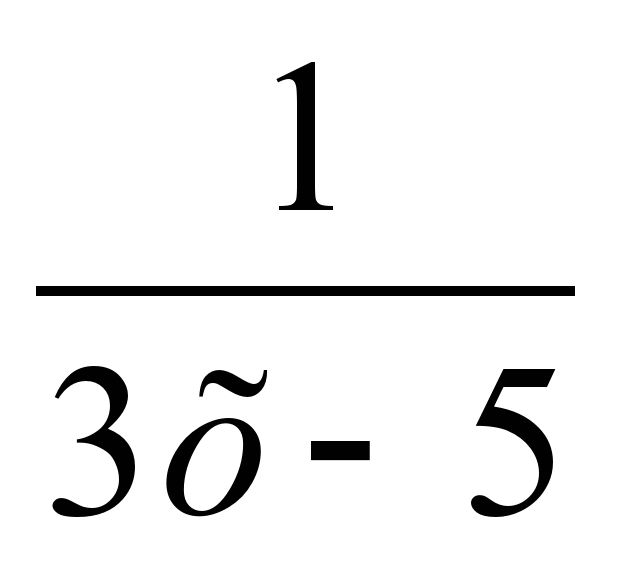 = log
= log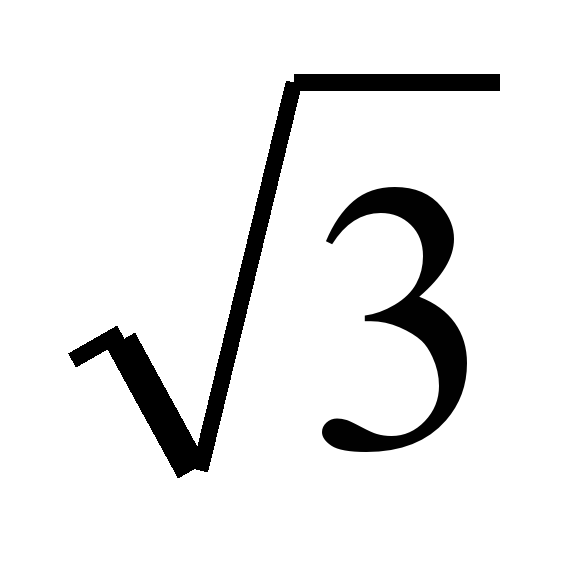 1 теңдеуін 1-ші мысалға қарап шеш
1 теңдеуін 1-ші мысалға қарап шеш
3) log0,252x+3 log 0,25x+5=0
log 0,25x =у алмастырып
у2+3у+5 =0 теңдеуін шеш
3.у-тің мәндерің қойып, lg10х =у теңдеілерді шешіңдер
4. . х-тің мәнің ММЖ-мен тексер.
Жауабы:
3)lоg52 x-lоg5x-3=0
1. ММЖ анықтайсын:
2. lоg5x =у алмастырып
у2-у-3 =0 теңдеуін шешіңіз
у-тің мәндерің қойып, lоg 5х =у теңдеілерді шешіңдер
4. . х-тің мәнің ММЖ-мен тексер.
Жауабы:
Тақырыпты меңгергенінде тексеріп көр:
1)lg(3-x)-lg(x+2)=2lg2
1. ММЖ анықтайсын: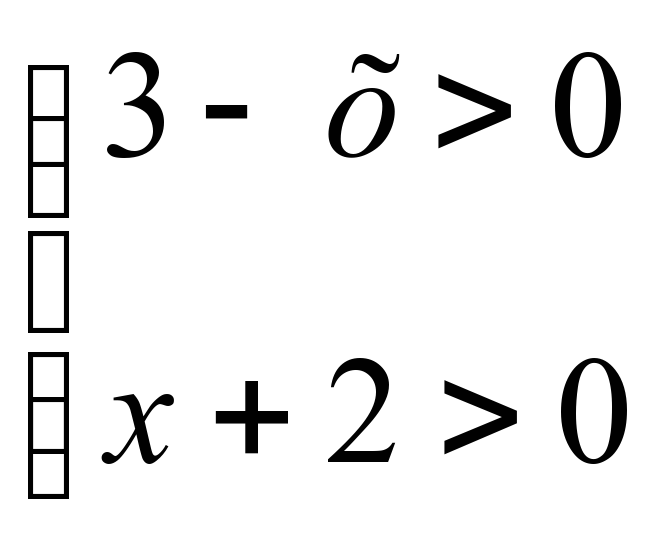 =
=
2. Логарифмнің қасиеттерін пайдаланып: lg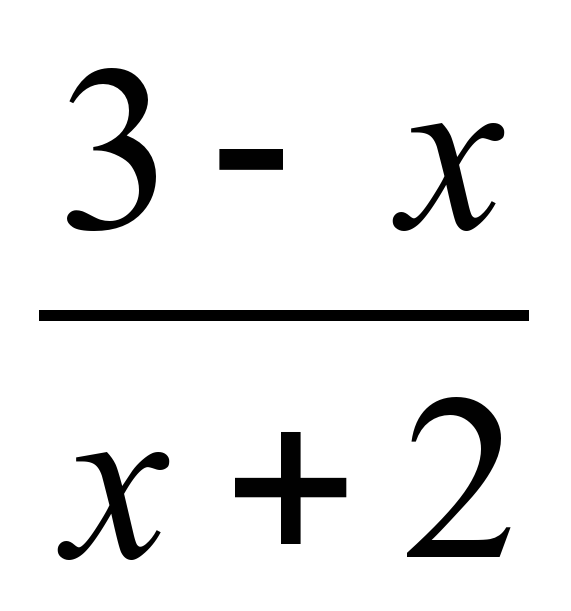 = lg4
= lg4
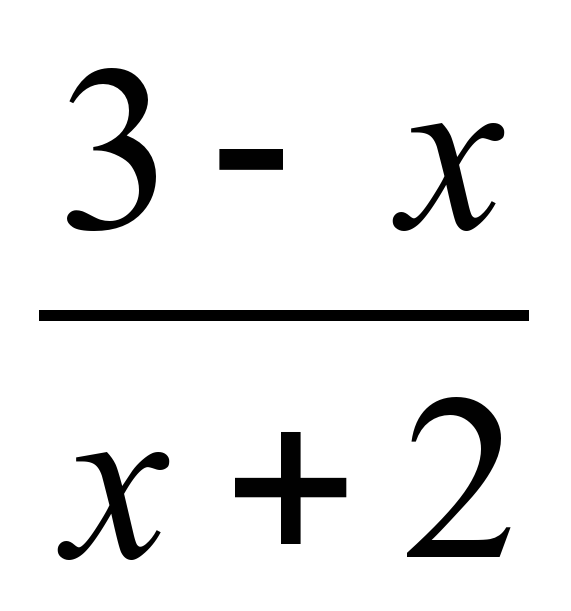 =4 теңдеуін шеш
=4 теңдеуін шеш
3. х-тің мәнің ММЖ-мен тексер.
Жауабы
2) log0.5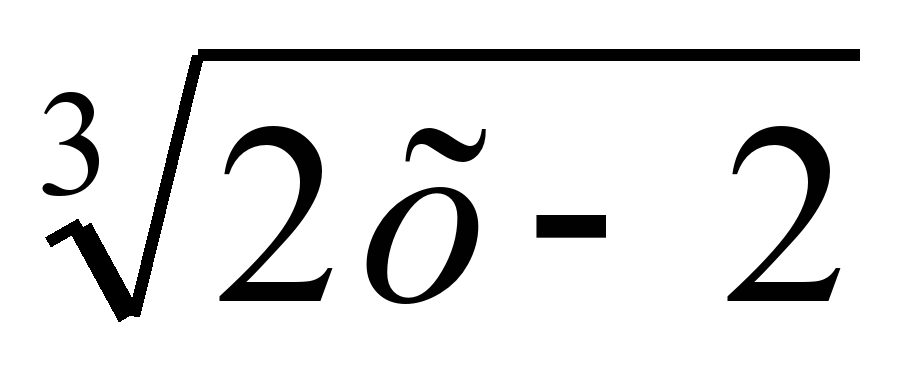 =-2
=-2
1. ММЖ анықтайсын: 2х-20 =
2. -2= log0.522 = log0.54 алмастырып теңді 1-ші мысалға қарап шеш
3. х-тің мәнің ММЖ-мен тексер.
Жауабы
3) log22х- 5log2х+6=0
1. ММЖ анықтайсын:
2. log2х =у алмастырып
у2-5у+6 =0 теңдеуін шешіңдер
3.у-тің мәндерің қойып, log2х =у теңдеілерді шешіңдер
4. . х-тің мәнің ММЖ-мен тексер.
Жауабы:
Тақырыпты меңгергенінде тексеріп көр:
1) lg(x2-x)=1-lg5
1. ММЖ анықтайсын: x2-x 0 =
2. Логарифмнің қасиеттерін пайдаланып: 1 = lg10 алмастырып және lg10- lg5 = lg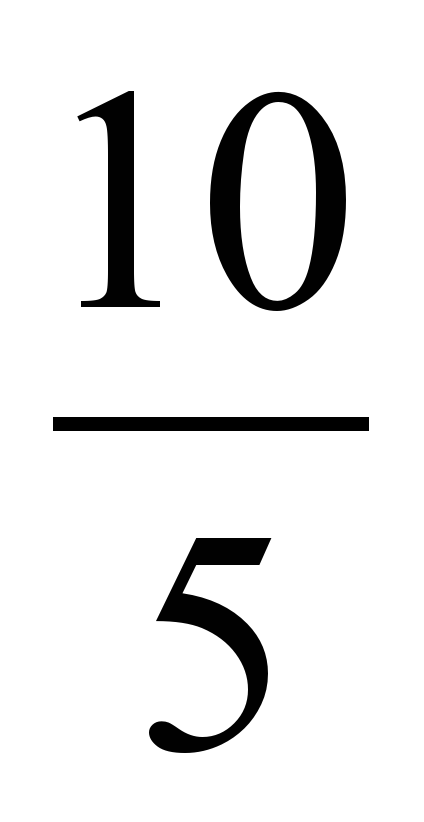 = lg2
= lg2
lg(x2-x)= lg2
х2-х =2 теңдеін шеш
. 3 х-тің мәнің ММЖ-мен тексер.
Жауабы
2) log3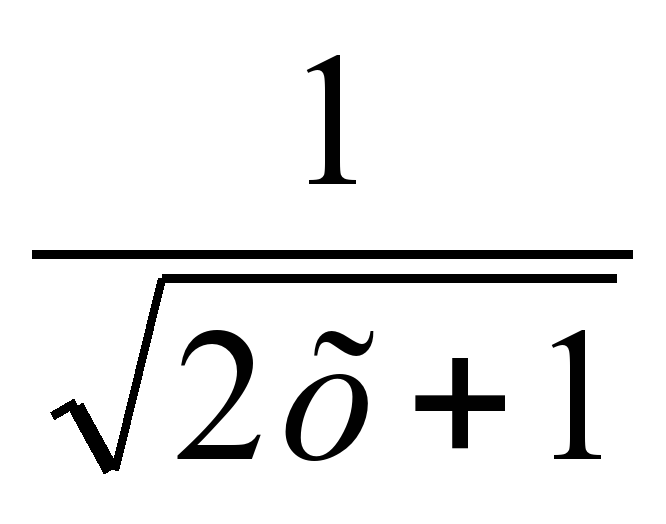 =-1
=-1
1. ММЖ анықтайсын: 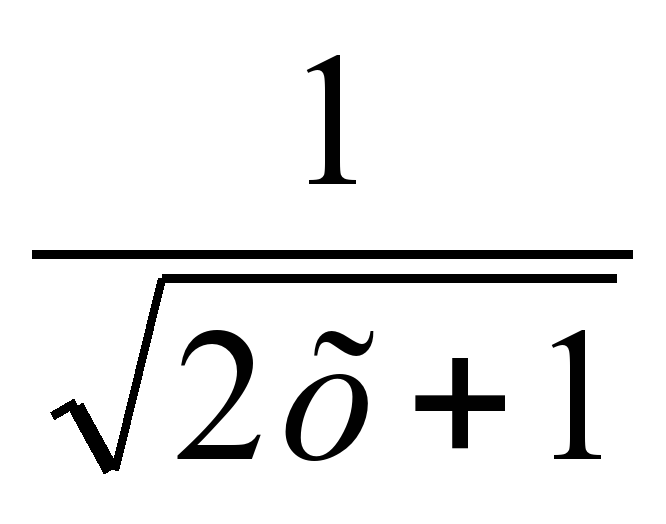 0 =
0 =
2. Логарифмнің қасиеттерін пайдаланып: -1 = log3 алмастыру қажет
алмастыру қажет
теңдеуін 1-ші мысалға қарап шеш
3. х-тің мәнің ММЖ-мен тексер.
Жауабы
3) lоg52x+lоg5x-2=0
1. ММЖ анықтайсын:
2.lоg5x =у алмастырып
у2+у-2 =0 теңдеін шешіңдер.
3.у-тің мәндерің қойып,
lоg 5х =у теңдеілерді шешіңдер
4. . х-тің мәнің ММЖ-мен тексер.
Жауабы:
Тақырыпты меңгергенінде тексеріп көр:
1) ln(x2-6x+9)=ln3+ln(x+3)
1. ММЖ анықтайсын: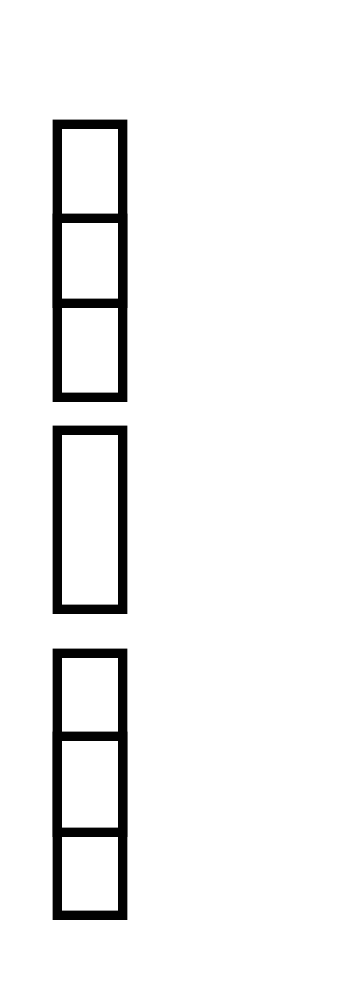
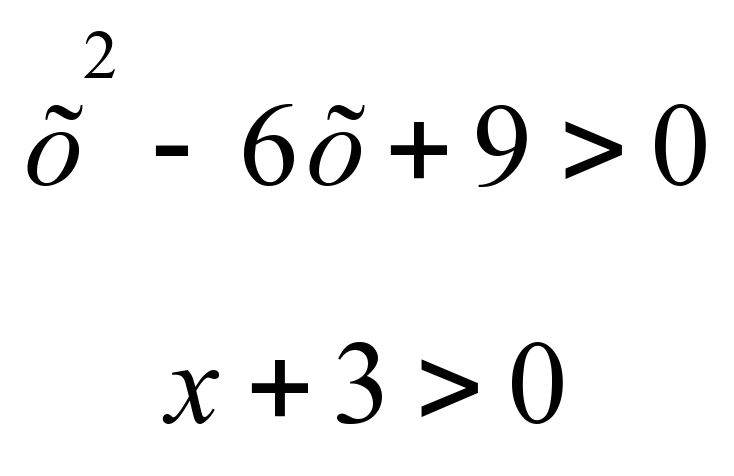 =
=
2. Логарифм қасиеттерін пайдалнып:
ln(x2-6x+9)= ln3(x+3) теңдеіне келтіріп
x2-6x+9 = 3(x+3) теңдеін шешіңдер
3 х-тің мәнің ММЖ-мен тексер.
Жауабы
2) log0.7
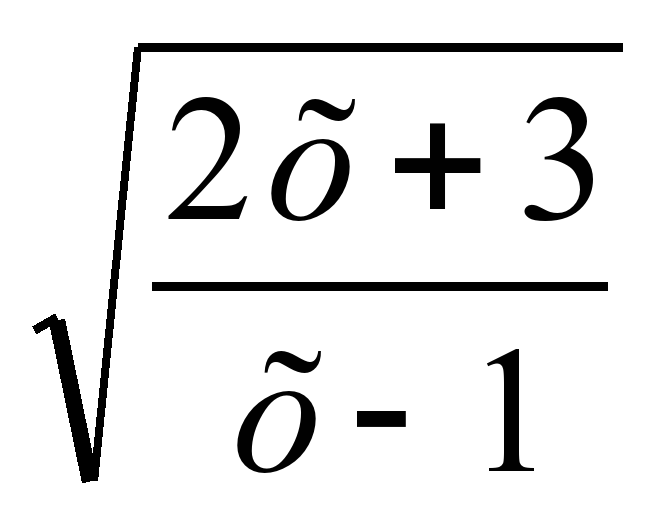 =0
=0
1. ММЖ анықтайсын: 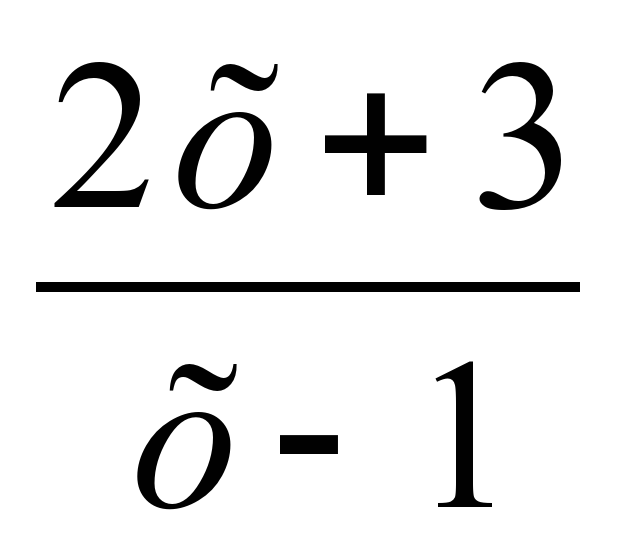 0 =
0 =
2. Логарифмнің қасиеттерін пайдаланып 0= log0.7 1 алмастырып
1 алмастырып
log0.7
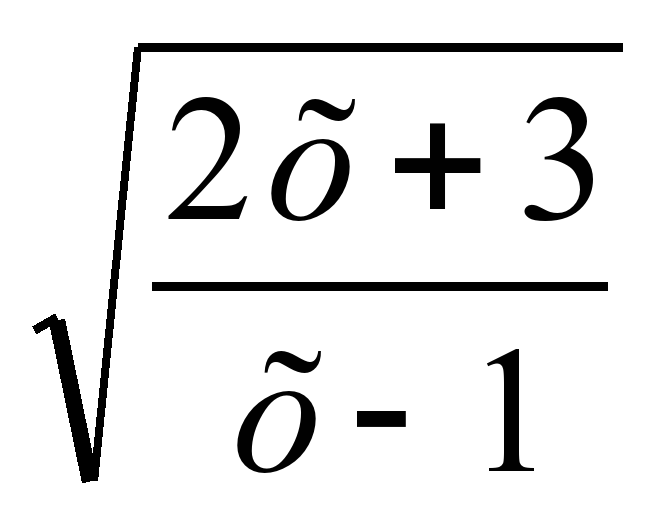 = log0.7
= log0.7 1
1
теңдеуін 1-ші мысалға қарап шеш
3 х-тің мәнің ММЖ-мен тексер.
Жауабы
3)lоg52 x-lоg5x-3=0
1. ММЖ анықтайсын:
2. lоg5x =у алмастырып
у2-у-3 =0 теңдеуін шешіңіз
у-тің мәндерің қойып, lоg 5х =у теңдеілерді шешіңдер
4. . х-тің мәнің ММЖ-мен тексер.
Жауабы:
Тест.
1. log3 x = log3 6 + log3 2.
2. 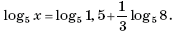
3. 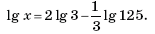
4. log2 x = 2log2 5 – log2 0,5.
5. 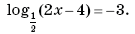
6. lg (3x – 8) = lg (x – 2).
7. log0,1 (6x – 11) = log0,1 (x – 2).
8. log0,5 x = 2log0,5 10 – log0,5 2.
9. log2 (3 – x) = 0.
10. log3 (5 + 2x) = 1.
11. lg x = lg 1,5 + 2lg 2.
12. lg2 x + 2lg x = 8.
13. log4 (2x – 5) = log4 (x + 1).
14. log6 (3x – 76) = log6 (x + 24).
15. lg (x2 – 2x – 4) = lg 11.
16. log7 x = 2log7 3 + log7 0,2.
17. 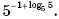
18. 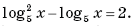
19. lg (3x + 8) = lg (x + 6).
20. log2 (4x – 5) = log2 (x – 14).
21. 
22. 
23. log5 (2x + 3) = log5 (x + 1).
24. 
25. lg (5x + 7) = lg (3x – 5).
26. log2 (x – 14) = 4.
27. logx (x2 – 2x + 2) = 1.
28. 
29. logx (x2 – 12x + 12) = 1.
30. log7 (46 – 3x) = 2.
31. log p (x2 + 2x + 3) = logp 6.
32. log3 (5x – 6) = log3 (3x – 2).
33. loga x = 2loga 3 + loga 5.
Ответы: 1. 12. 2. 3. 3. 1,8. 4. 50. 5. 6. 6. 3. 7. 1,8. 8. 50. 9. 2. 10. –1. 11. 6.
12. 10–4; 102. 13. 6. 14. 50. 15. –3; 5. 16. 1,8. 17. 1. 18. 0,2; 25.
19. –1. 20. Нет корней. 21. 2. 22. 45. 23. Нет корней. 24. 1. 25. Нет корней. 26. 30.
27. 2. 28. 6. 29. 12. 30. –1. 31. –3; 1. 32. 2. 33. 45.
| А | 1,8 | И | 2 | О | 
|
| В | 12 | К | –1 | Р | 1 |
| Г | 30 | Л | –3; 1 | С | 0,2; 25 |
| Д | 45 | М | 3 | Т | 50 |
| Е | 6 | Н | 10–4; 102 | Ц | –3; 5 |
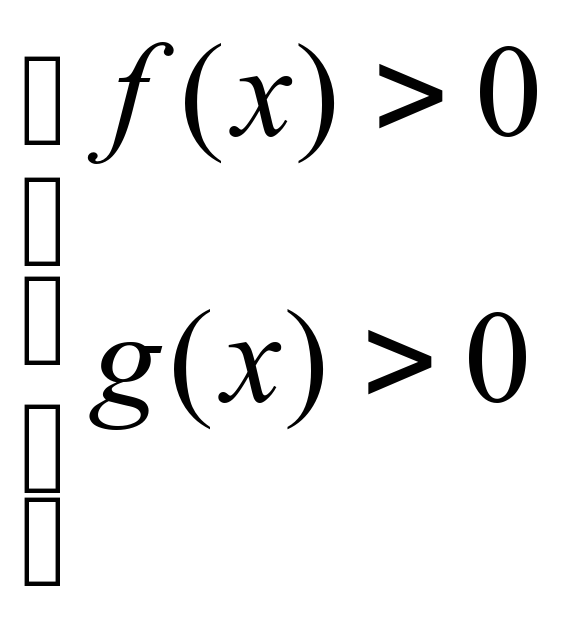
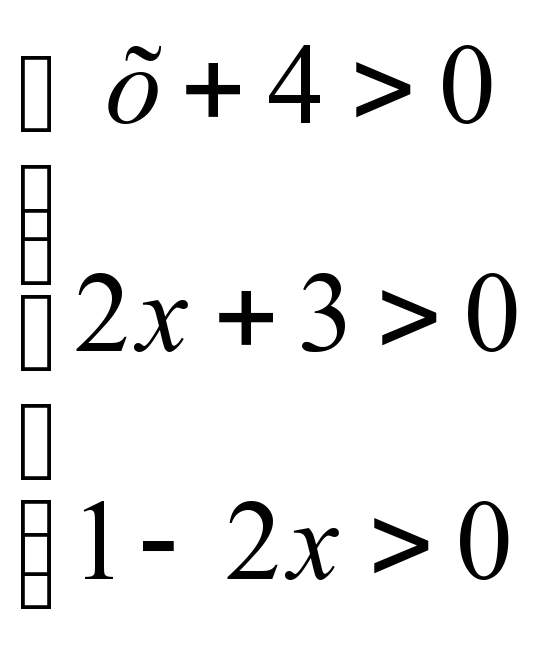 = -1.5
= -1.5 вадраттық теңдеудің түбірлерін ММЖ (-1,5;0,5) салыстырамыз -1с(-1,5;0,5) ал 0,5с(-1,5;0,5)
вадраттық теңдеудің түбірлерін ММЖ (-1,5;0,5) салыстырамыз -1с(-1,5;0,5) ал 0,5с(-1,5;0,5)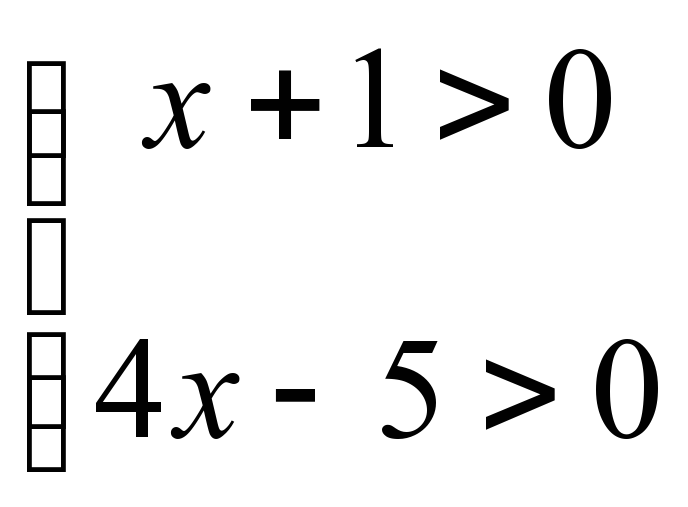 =
=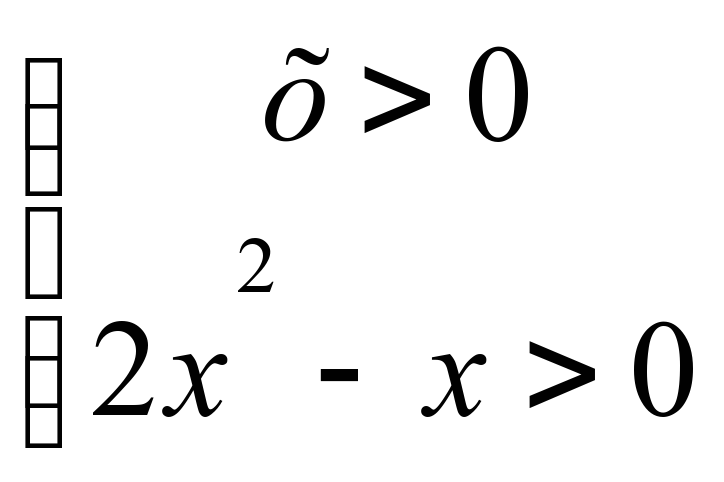 =
=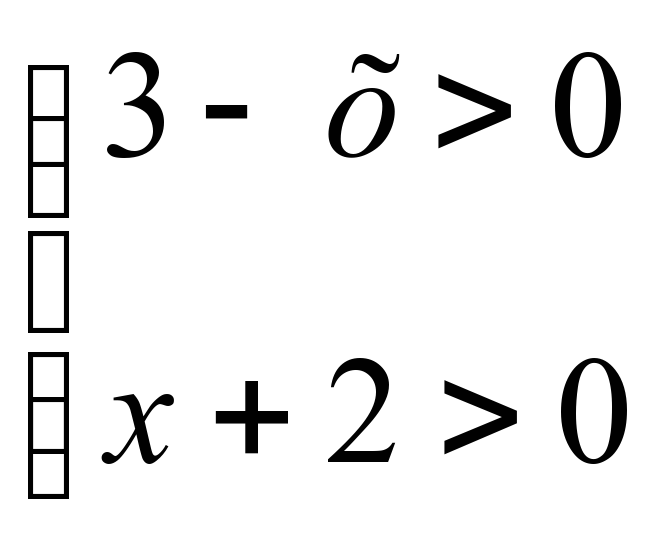 =
=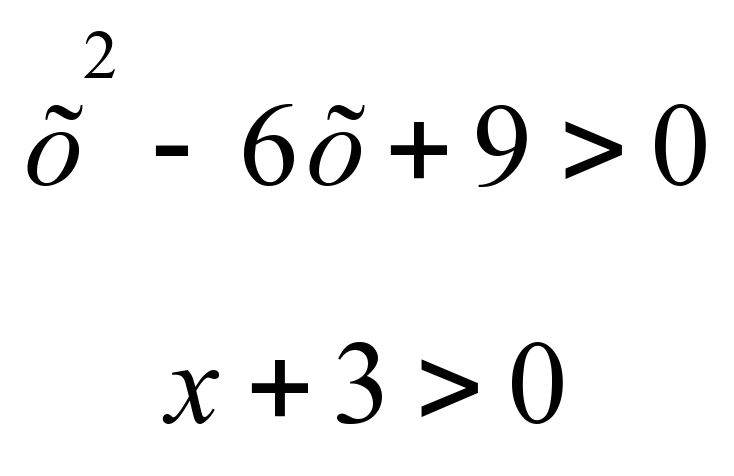 =
=















