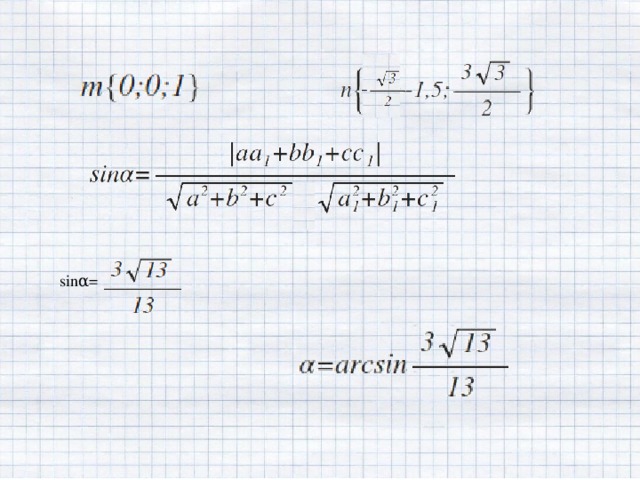План – конспект урока.
Тема: «Координатно – векторный способ решения заданий С2»
Слайд 1
Координатно – векторный способ решения задания С2
Слайд 2
Цель: «Общение и систематизация применение координатно – векторного способа при решении различных видов стереометрической задачи С2»
Слайд 3
Задание С2 Единого государственного экзамена представляет собой стереометрическую задачу на определение
- угла между прямыми
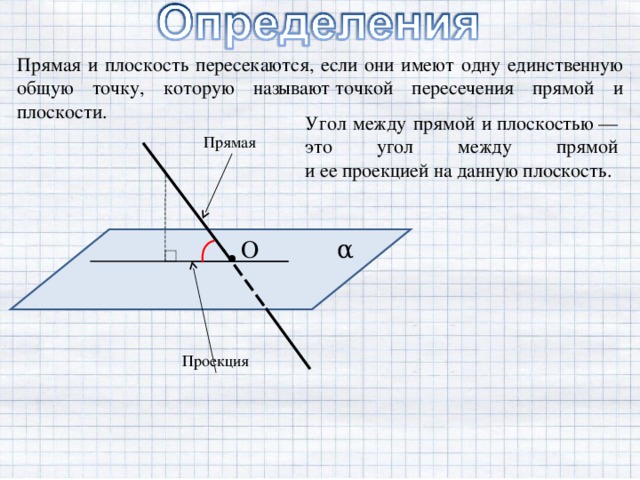
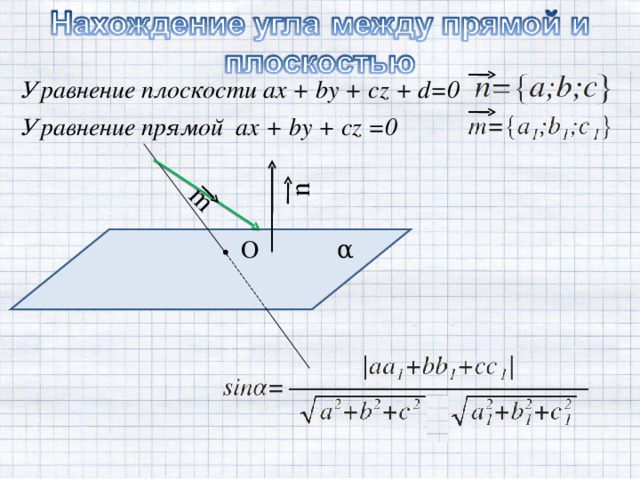
- угла между прямой и плоскостью
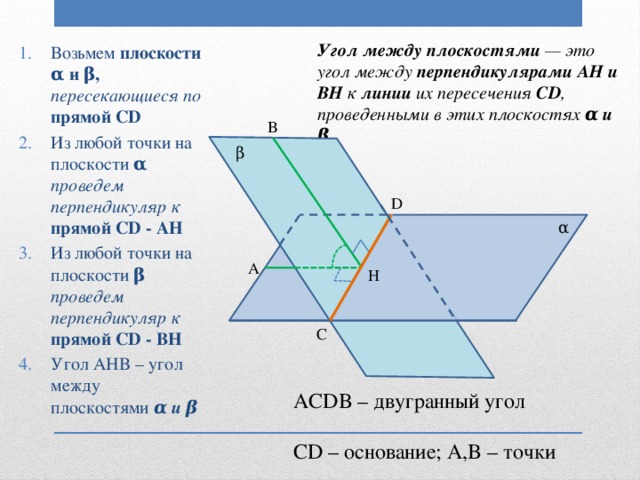
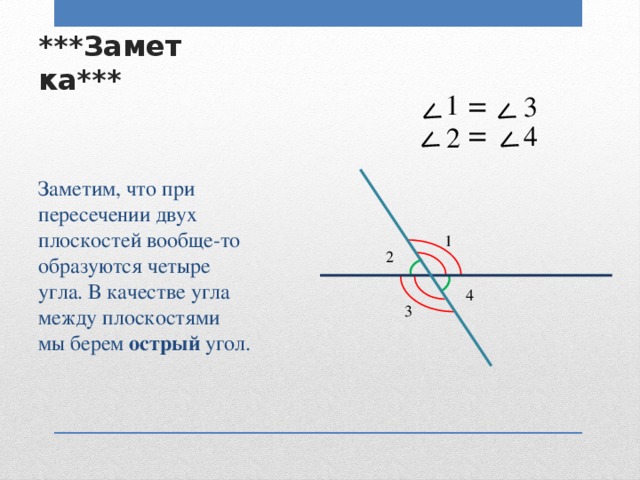
- угла между плоскостями
- расстояние между точками
- расстояние от точки до прямой
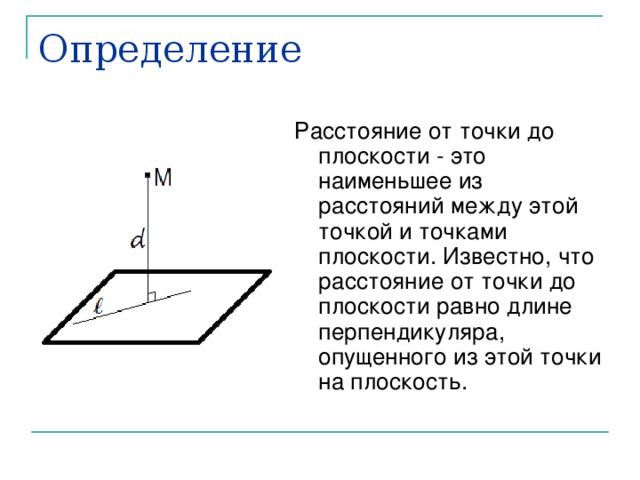
- расстояния от точки до плоскости
- расстояния между прямыми в пространстве.
Слайд 4
Вычисление определителя матрицы.
- Для работы на сегодняшнем уроке нам необходимо вспомнить правила вычисления определителей матриц.
- вычисление определителя матрицы 2 на 2
- вычисление определителя матрицы 3 на 3 двумя способами: разложением определителя по элементам первой строки и правило треугольника.
Слайд 5
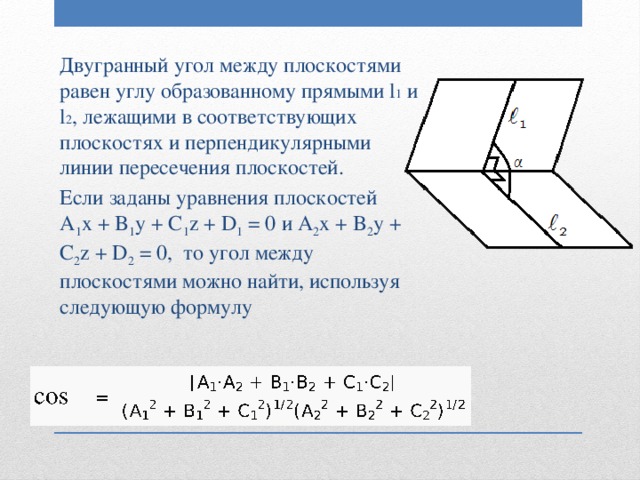
Уравнение плоскости, проходящей через три точки
. Если А(то уравнение плоскости имеет вид:
=
=Ax + By + Cz + D
Вектор нормали к этой плоскости имеет координаты
Слайд 6
Рассмотрим некоторые виды задач.
Ребята подготовили презентации и решение задач на заданную тему.
Слайд 7,8
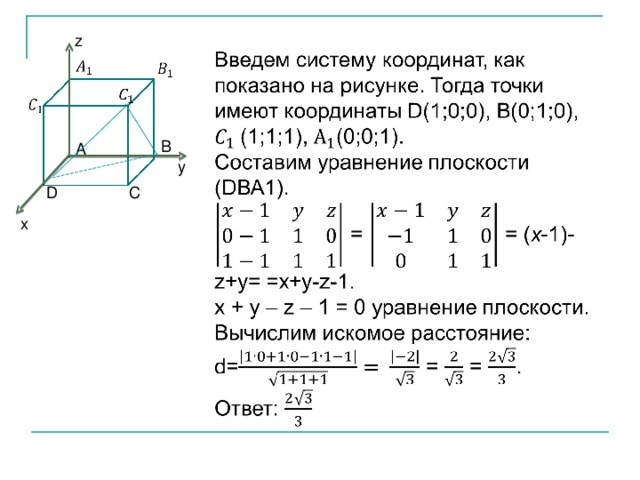
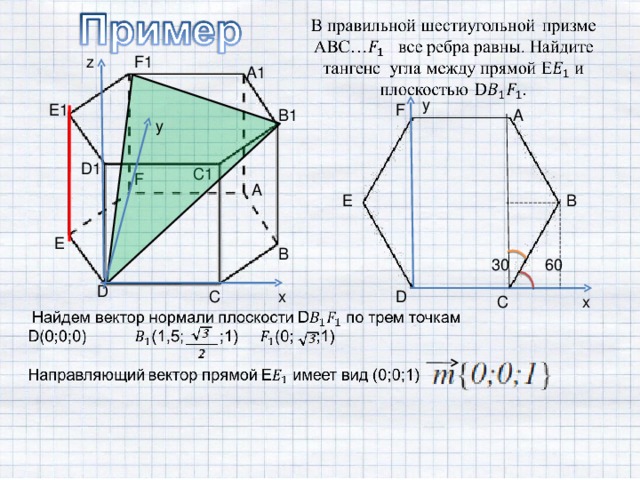
А теперь рассмотрим задачу С2 , предлагаемую на ЕГЭ 2012 года. Задача на нахождение угла между плоскостями. Решение этой задачи рассмотрим координатно- векторным способом и традиционным.
Слайд 9.
задача на вычисление расстояния между скрещивающими прямыми в правильной шестиугольной пирамиде.
Слайд 10,11
А теперь подведём итоги.
Применяя координатно – векторный способ решения задач С2, что необходимо сделать в первую очередь?
-правильно задать систему координат.
--Вычисление координат вектора
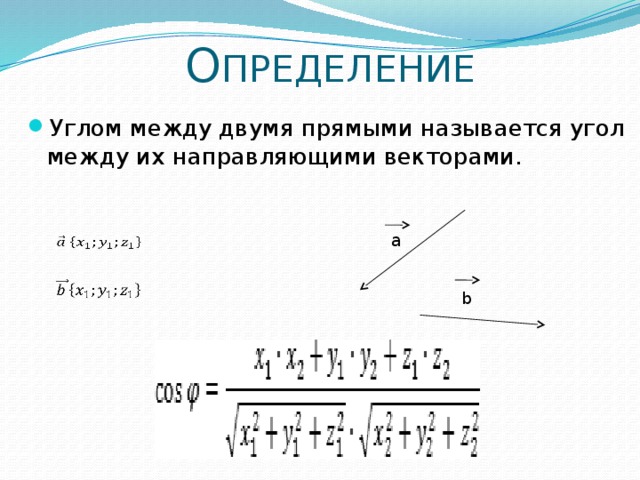
--Вычисление угла между направляющими векторами прямых.
- Вычисление угла между плоскостями. вектора нормалей к плоскостям.
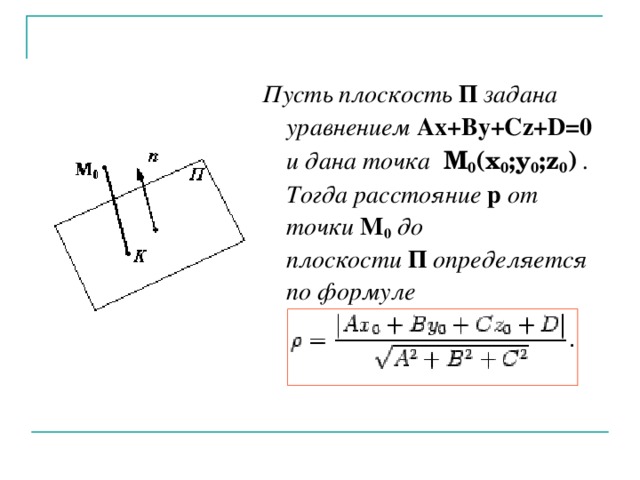
- Расстояние от точки M до плоскости α, имеющей уравнение Ax+By+Cz+D=0.
--Расстояние между скрещивающими прямыми k и h, если А направляющий вектор прямой k, направляющий вектор прямой h.
Слайд 12
Домашнее задание: предложенную задачу решить 2 способами и сделать вывод о рациональности этого способа.
На этом занятии нам хотелось вам показать красоту, рациональность и простоту координатно – векторного способа. Мы надеемся, что вам он понравился!
Слайд 13
Задание С2 Единого государственного экзамена представляет собой стереометрическую задачу на определение расстояний или углов в пространстве между объектами, связанными с некоторыми многогранниками.
Решение задания С2 оценивается 2 баллами. Один балл начисляется за правильное построение или описание искомого угла или расстояния. Ещё один балл начисляется за правильно проведенные вычисления и верный ответ.
По итогам ЕГЭ 2012 года очень мало работ было оценено в 2 балла. Основные проблемы: неумение строить линейные углы и проекции, вычислительные ошибки. Многие выпускники демонстрировали непонимание нахождения угла между прямой и плоскостью, между плоскостями.
При нахождении углов в пространстве возникают трудности с дополнительными построениями и необходимыми обоснованиями, сопровождающими эти построения.
Слайд 14
Координатно – векторный метод позволяет избежать трудностей в построении и вычислении углов и расстояний между объектами в пространстве. От выпускников требуется знание нескольких формул и навыки в решении простейших задач, основная нагрузка при решении задач приходится на вычислительную часть.
Практика показывает, что учащиеся быстро осваивают метод координат, так как при его использовании необходимо придерживаться общего алгоритма: вычислить координаты необходимых точек, расположенных на многограннике, и применить соответствующую формулу. Для некоторых задач дополнительно требуется умение составлять уравнение плоскости.
Удачный выбор системы координат позволяет значительно упростить вычисления.
Слайд 15
Цели, которые я ставила перед собой.
• образовательные: научить применять полученные знания на практике; оперировать имеющимся потенциалом в конкретной ситуации; закрепить умения и навыки работы с изученными формулами.
• развивающие: совершенствовать умения работы с источниками знаний; совершенствовать навыки анализа, обобщения; развивать творческие способности; закрепить умения поиска рационального решения задачи.
• воспитательные: вовлечь в активную деятельность; формировать культуру общения, совершенствовать навыки общения, научить отстаивать свою точку зрения; развивать коммуникативные навыки работы в группах.