Урок геометрии в 10 классе.
Тема урока: «Теорема о трех перпендикулярах».
Тип урока: урок закрепления нового материала.
Цель урока:
обучающая:
Закрепить изученный теоретический материал на практике, обосновать необходимость теоремы о трех перпендикулярах;
Сформировать видение изученной закономерности в различных ситуациях: при решении задач на доказательство или задач, требующих найти численное (буквенное) значение, какого – либо элемента;
Учить умению читать чертеж;
Учить умению объяснять, комментировать выполняемое упражнение в виде цельного связного рассказа.
развивающая:
Способствовать развитию общения как метода научного познания, аналитико-синтетического мышления, смысловой памяти и произвольного внимания;
Развивать навыки исследовательской деятельности (выдвижение гипотез, анализ и обобщение полученных результатов).
воспитательная:
Развивать у учащихся коммуникативные компетенции (культуру общения, умение работать в группах, элементы ораторского искусства);
Способствовать развитию творческой деятельности учащихся, потребности к самообразованию.
Ход урока
Организационный момент – 1 минута.
Учитель приветствует учащихся и объявляет цель урока и план, используя презентационное сопровождение. Зачитывает эпиграф к уроку.
Учитель. (Слайды 1-4) Сегодня на уроке мы закрепим теорему о трех перпендикулярах, научимся применять теорему о трех перпендикулярах при решении разнообразных задач, вы убедитесь, насколько удобна теорема в использовании и насколько упрощается решение задачи с ее помощью. Проверка домашнего задания – 16 минут.
Учитель. Дома вы должны были выучить доказательство теоремы о трех перпендикулярах, рассмотренное на прошлом уроке, и, разбившись на группы, подготовить и презентовать другие способы доказательства теоремы. А начнем мы с проверки теоретических знаний, используемых при подготовке домашнего задания. (Слайд 5 - 6)
Учитель. Ответьте на вопросы и проведите самооценку своего устного ответа, сопоставив его с выводимыми на экран элементами опорного конспекта.
Учитель объясняет метод теоретического опроса. Подает вопросы по теории на слайдах презентации. Демонстрирует после ответов учащихся соответствующие элементы опорного конспекта.
Учащиеся отвечают на теоретические вопросы устно. После демонстрации правильных ответов ими проводится самооценка своего устного ответа.
Вопросы:
Угол между прямыми равен 90º. Как называются такие прямые?
/перпендикулярные/
Верно ли утверждение: «Прямая называется перпендикулярной плоскости, если она перпендикулярна некоторой прямой, лежащей в этой плоскости»?
/да/
Сформулируйте признак перпендикулярности прямой и плоскости.
/Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости./
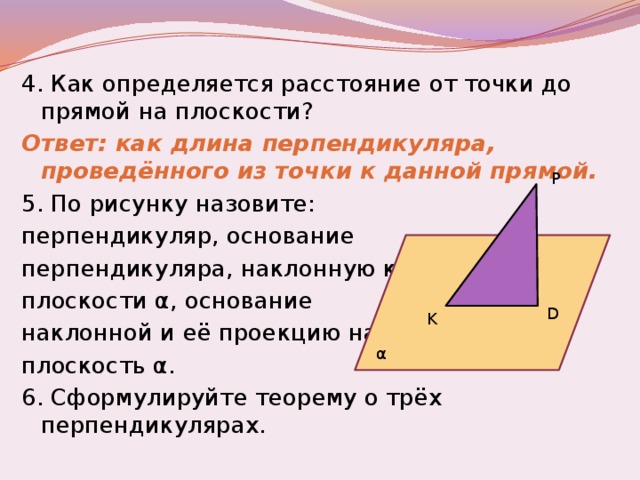
Как определяется расстояние от точки до прямой на плоскости?
/как длина перпендикуляра, поведенного из точки к данной прямой./
По рисунку 1 назовите: перпендикуляр, основание перпендикуляра, наклонную к плоскости α, основание наклонной, проекцию наклонной на плоскость α.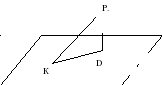
/ PD- перпендикуляр, точка D- основание перпендикуляра,PK- наклонная, точка K – основание наклонной, KD – проекция./
Сформулируйте теорему о трех перпендикулярах. (Слайд 7 - 8)
Теорема.
Прямая, проведенная в плоскости через основание наклонной перпендикулярно к е проекции на эту плоскость, перпендикулярна и к самой наклонной.
Обратно: Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к ее проекции.
Задача №154 (Слайд 17)
Дано: 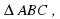 BD ┴ (ABC), BD = 9 см, АС = 10 см, ВС = ВА = 13 см.
BD ┴ (ABC), BD = 9 см, АС = 10 см, ВС = ВА = 13 см.
Найти: а) расстояние от точки D до АС; б) S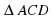 .
.
Решение:
а) 1. DB – перпендикуляр, АС и DA – наклонные, так как ВА = ВС – проекции, то DA=DC.
2. 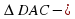 равнобедренный, DK – высота, медиана и биссектриса, DK – расстояние от точки D до АС.
равнобедренный, DK – высота, медиана и биссектриса, DK – расстояние от точки D до АС.
3. 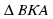 ,
, 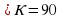 , ВК =
, ВК =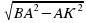 , ВК =
, ВК = 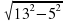 =
= 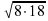 = 12 (см).
= 12 (см).
4. 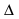 DBK,
DBK,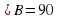 , DK =
, DK = 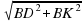 , DK =
, DK = 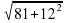 =
= 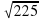 = 15 (см).
= 15 (см).
б) S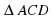 =
= 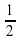 ·AC·DK, S
·AC·DK, S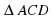 =
= 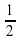 ·10·15= 75 (см2).
·10·15= 75 (см2).
Ответ: 15 см, 75 см2.
Задача №158 (Слайд 18)
Через вершину В ромба АВСD проведена прямая ВМ перпендикулярно к его плоскости. Найти расстояние от точки М до прямых, содержащих стороны ромба, если АВ = 25 см;
D = 60º; ВМ = 12,5 см.
Решение:
Проведем ВК ┴ AD. ВК – проекция наклонной МК на плоскость ромба; AD ┴ ВК, то AD ┴ МК (по теореме о трех перпендикулярах). Длина МК – расстояние от точки М до прямой AD . МЕ – расстояние от точки М до прямой DC.
Из треугольника АВК: ВК = АВsin60º = 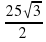 .
.
 МВК – прямоугольный (
МВК – прямоугольный (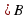 = 90º), так как МВ ┴ (АВС); МК =
= 90º), так как МВ ┴ (АВС); МК = 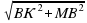 = 25 (см).
= 25 (см).
ВК = ВЕ (как высоты ромба); 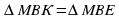 (по двум катетам, как прямоугольные); МЕ = МК = 25 (см).
(по двум катетам, как прямоугольные); МЕ = МК = 25 (см).
Расстояние от точки М до прямых АВ и ВС равны длине перпендикуляра МВ, то есть 12,5 см.
Ответ: 25 см; 25 см; 12,5 см; 12,5 см.
Задача №161 (Слайд 19)
Луч ВА не лежит в плоскости неразвернутого угла CBD. Докажите, что если
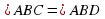 , причем
, причем 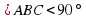 ,то проекцией луча ВА на плоскость CBD является биссектриса CBD.
,то проекцией луча ВА на плоскость CBD является биссектриса CBD.
Решение:
1). Пусть АЕ ┴ (CBD). В плоскости (АВС) проведем перпендикуляр АМ к прямой ВС, а в плоскости (АВD) перпендикуляр АК к прямой BD.
Так как 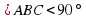 ,то точка М лежит на луче ВС (а не на продолжении этого луча). Аналогично, так как ABD BD. Так как ВС ┴ АМ, то ВС┴ ЕМ (по теореме, обратной теореме о трех перпендикулярах).
,то точка М лежит на луче ВС (а не на продолжении этого луча). Аналогично, так как ABD BD. Так как ВС ┴ АМ, то ВС┴ ЕМ (по теореме, обратной теореме о трех перпендикулярах).
Аналогично доказывается, что BD ┴ ЕК.
2). 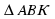 =
= 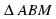 по гипотенузе (АВ – общая сторона) и острому углу (ABD), то ВМ = ВК;
по гипотенузе (АВ – общая сторона) и острому углу (ABD), то ВМ = ВК;
3). 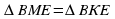 по гипотенузе (ВЕ – общая сторона) и катету (ВМ = ВК), то ЕМ = ЕК;
по гипотенузе (ВЕ – общая сторона) и катету (ВМ = ВК), то ЕМ = ЕК;
4). Точка Е равноудалена от сторон D, значит, она лежит на биссектрисе этого угла, то есть луч ВЕ – биссектриса 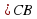 D.
D.
Самостоятельное выполнение учащимися заданий под контролем учителя.
1). Учитель демонстрирует тестовые задания, зачитывает условие с экрана. Учащиеся самостоятельно отвечают на вопросы. Для проверки обмениваются тетрадями в статических группах.
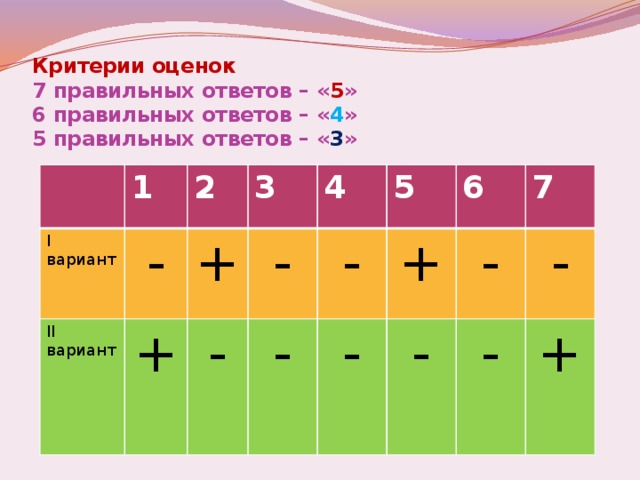
Учитель: Ребята, сейчас отвечая на вопросы тестовых заданий, вы должны установить истинность или ложность утверждения, тем самым отметив на таблице соответственно знаками «+» и «-», после чего произведите взаимопроверку, сверяя ответы с образцом. (Слайд 20 -21)
Верно ли, что две прямые, параллельные одной плоскости, перпендикулярны (две прямые, перпендикулярные к одной плоскости параллельны)?
Может ли прямая, перпендикулярная к плоскости, скрещиваться с прямой, лежащей в этой плоскости (прямая, перпендикулярная к плоскости, быть параллельна прямой, лежащей в этой плоскости)?
Верно ли, что прямая перпендикулярна к плоскости, если она перпендикулярна к двум прямым этой плоскости (она перпендикулярна к двум прямым, параллельным этой плоскости)?
Могут ли две скрещивающиеся прямые быть перпендикулярными к одной плоскости (две пересекающиеся прямые быть перпендикулярными к одной плоскости)?
Верно ли, что любая из трех взаимно перпендикулярных прямых перпендикулярна к плоскости двух других прямых (две прямые в пространстве, перпендикулярные к третьей, параллельны)?
Могут ли пересекаться две плоскости, перпендикулярные к одной прямой (прямая а и плоскость α, перпендикулярные к одной прямой с)?
Верно ли, что длина перпендикуляра меньше длины наклонной, проведенной из той же точки (длина перпендикуляра меньше длины проекции наклонной, проведенной из той же точки)?
(Слайд 22)
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| I вариант | - | + | - | - | + | - | + |
| IIвариант | + | - | - | - | - | - | + |
Критерии оценок:
7 правильных ответов – «5»,
6 правильных ответов – «4»,
5 правильных ответов – «3».
2). Самостоятельное решение задач (Слайд 23)
Каждому учащемуся раздается карточка с разноуровневыми задачами. Задача 3 уровня на оценку «5», 2уровня – на «4», 1 уровня – на «3». Каждый выбирает себе уровень сложности и решает задачу, по истечении времени работы сдаются на проверку.
I уровень.
Дано: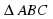 , АС ┴ ВС, SA = SB = SC =10 см; СМ =5 см –медиана.
, АС ┴ ВС, SA = SB = SC =10 см; СМ =5 см –медиана.
Найти: SM (расстояние от точки S до плоскости (АВС).
Решение:
Прямая SM, М – середина гипотенузы АВ, перпендикулярна к плоскости (АВС) SM ┴ (АВС).
SM =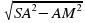 =
=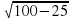 =
= 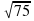 =5
=5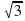 (см).
(см).
Ответ: 5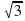 (см).
(см).
II уровень
Дано: ABCD – прямоугольник; АК ┴ (АВС), KD= 6 см, КВ = 7 см, КС = 9 см.
Найти: расстояние от точки К до (АВС).
Решение: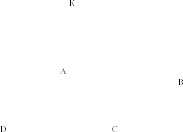
Длина АК – расстояние от К до (АВС) по определению.
Так как DC ┴ AD, AD проекция KD, то по ТТП KD┴DC, значит, в 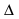 KDC
KDC 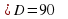 . KC2 = KD2 + DC2, DC =
. KC2 = KD2 + DC2, DC = 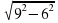 =
= 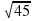 = 3
= 3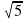 (см).
(см).
СВ┴КВ по ТТП; СВ = 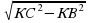 ; СВ = 4
; СВ = 4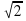 (см).
(см).
Из 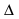 ADC , AC =
ADC , AC =  (см).
(см).
ИЗ 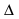 КСА A = 90º, KA =
КСА A = 90º, KA =  , KA =2 (см).
, KA =2 (см).
Ответ: 2 см.
III уровень.
Дано: АВ = 17 см, АС = 15 см, ВС = 8 см, АМ ┴ (АВС),
АМ = 20 см.
Найти: МЕ.
Решение:

1.В 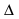 АВС против меньшей стороны лежит меньший угол (по теореме синусов). Проведем АЕ ┴ ВС, АЕ ┴ МЕ. По теореме о трех перпендикулярах МЕ ┴ ВС.
АВС против меньшей стороны лежит меньший угол (по теореме синусов). Проведем АЕ ┴ ВС, АЕ ┴ МЕ. По теореме о трех перпендикулярах МЕ ┴ ВС.
2. По формуле Герона:
S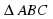 = , S
= , S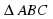 =
=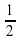 BC·AE.
BC·AE.
P =  = 20, S
= 20, S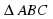 =
= = 60.
= 60.
AE = 15 (см).
По теореме Пифагора: МЕ =  , МЕ = 25 (см).
, МЕ = 25 (см).
Ответ: 25 см.
Подведение итогов урока.
1). Учитель предлагает обобщить учащимся весь теоретический материал, используемый на уроке и решить задачу, которая продемонстрирует успех изучения теоремы о трех перпендикулярах. Выставляются оценки за урок.
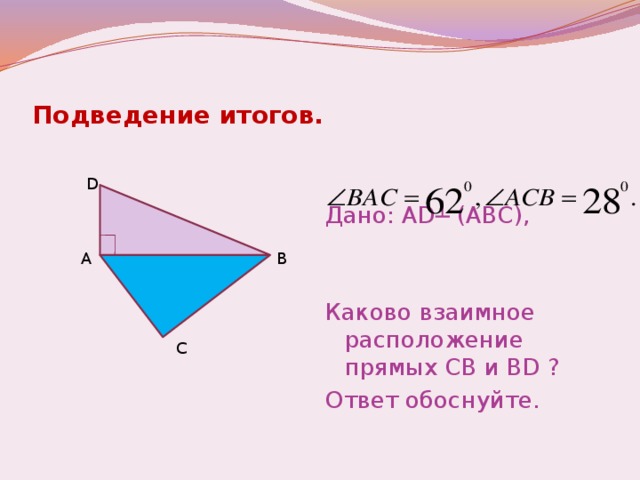
Задача.
Дано: AD ┴ (ABC), BAC = 62º, ACB = 28º.
Каково взаимное расположение прямых СВ и BD ? Ответ обоснуйте.
(Слайд 24)
2). Учитель выводит на экран обязательную и необязательную части домашнего задания. (Слайд 25). Учащиеся записывают задание.
ДЗ: №145, №143, №140, п.19,20.
Дополнительная задача:
Через сторону АD ромба ABCD проведена плоскость α. Найдите расстояние от прямой ВС до плоскости α, если S ромба = 80 см2, высота равна 8 см, а угол между проекцией стороны CD и прямой AD равен 45º.
4

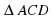

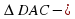 равнобедренный,
равнобедренный, 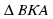 ,
, 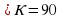 , ВК =
, ВК =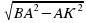 , ВК =
, ВК = 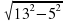 =
= 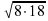 = 12 (см).
= 12 (см).
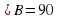 ,
, 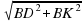 ,
, 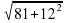 =
= 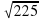 = 15 (см).
= 15 (см).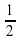

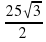 .
. = 90º), так как МВ ┴ (АВС); МК =
= 90º), так как МВ ┴ (АВС); МК = 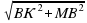 = 25 (см).
= 25 (см).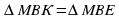 (по двум катетам, как прямоугольные); МЕ = МК = 25 (см).
(по двум катетам, как прямоугольные); МЕ = МК = 25 (см).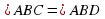 , причем
, причем 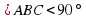 ,то проекцией луча ВА на плоскость
,то проекцией луча ВА на плоскость 
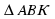 =
= 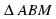 по гипотенузе (АВ – общая сторона) и острому углу (ABD), то ВМ = ВК;
по гипотенузе (АВ – общая сторона) и острому углу (ABD), то ВМ = ВК;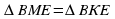 по гипотенузе (ВЕ – общая сторона) и катету (ВМ = ВК), то ЕМ = ЕК;
по гипотенузе (ВЕ – общая сторона) и катету (ВМ = ВК), то ЕМ = ЕК;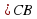
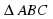 , АС ┴ ВС,
, АС ┴ ВС, 
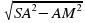
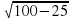 =
= 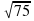 =5
=5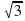 (
(
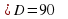 .
. 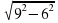 =
= 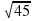 = 3
= 3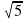 (
(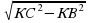 ; СВ = 4
; СВ = 4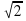 (см).
(см).