ИСПОЛЬЗОВАНИЕ ЭВРИСТИЧЕСКИХ ПРИЕМОВ В КУРСЕ АЛГЕБРЫ 9 КЛАССА
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Использование эвристических приемов в курсе алгебры 9 класса
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Использование эвристических приемов в курсе алгебры 9 класса»
Полезное для учителя
Распродажа видеоуроков!
2000 руб.
2860 руб.
1970 руб.
2820 руб.
1740 руб.
2480 руб.
1790 руб.
2560 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
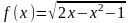 .
.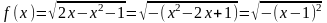 . Подкоренное выражение должно быть неотрицательным
. Подкоренное выражение должно быть неотрицательным 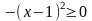 , но, так как,
, но, так как, 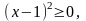 получаем систему двух неравенств
получаем систему двух неравенств 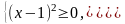 Таким образом, множество значений функции
Таким образом, множество значений функции 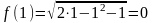 .
.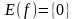 .
.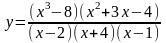 .
.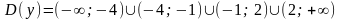 . Для нахождения множества значений функции преобразуем ее:
. Для нахождения множества значений функции преобразуем ее: 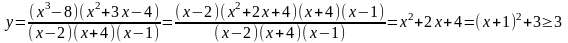 при
при 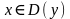 . Но учитывая, что
. Но учитывая, что 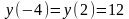 , находим
, находим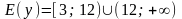
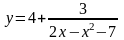 .
.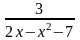 принимает наименьшее значение, то есть когда ее знаменатель – квадратный трехчлен
принимает наименьшее значение, то есть когда ее знаменатель – квадратный трехчлен 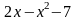 принимает наибольшее значение. Выделяем полный квадрат:
принимает наибольшее значение. Выделяем полный квадрат: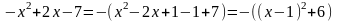 , таким образом, значение квадратного трехчлена тем больше, чем меньше выражение в скобках: наибольшее значение квадратного трехчлена, равное -6, достигается при
, таким образом, значение квадратного трехчлена тем больше, чем меньше выражение в скобках: наибольшее значение квадратного трехчлена, равное -6, достигается при 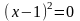 , то есть при
, то есть при 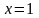 .
. 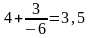 .
.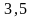 .
.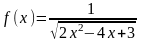 .
.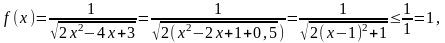 так как
так как 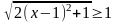 , причем равенство достигается при х =1.
, причем равенство достигается при х =1.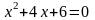 не имеет действительных корней.
не имеет действительных корней. 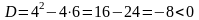 , следовательно, действительных корней нет, что и требовалось доказать.
, следовательно, действительных корней нет, что и требовалось доказать.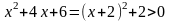 при любом значении x, значит, действительных корней уравнение не имеет.
при любом значении x, значит, действительных корней уравнение не имеет.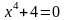 .
.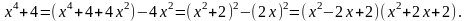
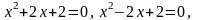 каждое из которых не имеет действительных корней.
каждое из которых не имеет действительных корней.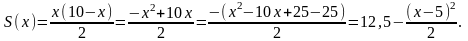
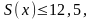 следовательно, на вопрос задачи ответ отрицательный: наибольшее значение площади треугольника достигается при x =5 и равно 12,5.
следовательно, на вопрос задачи ответ отрицательный: наибольшее значение площади треугольника достигается при x =5 и равно 12,5.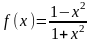 .
.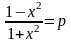 и рассмотрим равенство как уравнение с неизвестным х и параметром p.
и рассмотрим равенство как уравнение с неизвестным х и параметром p. 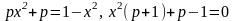 – квадратное уравнение (при
– квадратное уравнение (при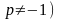 относительно х. Квадратное уравнение имеет действительные решения тогда и только тогда, когда его дискриминант неотрицателен:
относительно х. Квадратное уравнение имеет действительные решения тогда и только тогда, когда его дискриминант неотрицателен: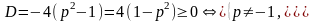 .
. 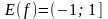 .
.
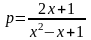 как уравнение с неизвестным x и параметром p. После преобразования получим:
как уравнение с неизвестным x и параметром p. После преобразования получим: 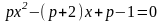 . Для того, чтобы это уравнение имело решение, необходимо и достаточно, чтобы выполнялось неравенство
. Для того, чтобы это уравнение имело решение, необходимо и достаточно, чтобы выполнялось неравенство 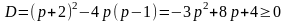 , откуда
, откуда 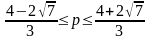 или
или 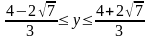 . Слева в неравенстве стоит наименьшее значение y, справа – наибольшее. Границы изменения y дают ответ на вопрос задачи.
. Слева в неравенстве стоит наименьшее значение y, справа – наибольшее. Границы изменения y дают ответ на вопрос задачи.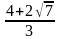 , наименьшее
, наименьшее 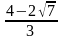 .
. рассматриваем данное равенство как уравнение с неизвестным x и параметром y=p и решаем задачу: при каких значениях параметра p это уравнение имеет решение.
рассматриваем данное равенство как уравнение с неизвестным x и параметром y=p и решаем задачу: при каких значениях параметра p это уравнение имеет решение.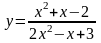 .
.















