Интегрированный урок математики и информатики в 9-м классе по теме: "Построение и преобразование графиков квадратичной функции" Составили: Ревко И.В., учитель математики ГБС(К)ОУ « Трубчевская школа-интернат IV вида» Ермакова Т.Н., учитель информатики ГБС(К)ОУ «Трубчевская школа-интернат IV вида» Тип урока: урок закрепления и совершенствования полученных знаний, интерактивная лабораторная работа с использованием компьютера.
Технология урока: интегрированный урок (математика + информатика).
Результат урока нацелен на овладение учащимися программным и дополнительным материалом по данной теме и рассчитан на выход каждого ученика, на свой уровень развития.
Оборудование и материалы: 6 ПК (установлена операционная система Windows XP, мультимедиапроектор, тесты, справочники, карточки-консультанты).
Подготовка к уроку: В «Мои документы» поместить файл «Практическая работа», тест, подготовить презентацию «Развитие понятия «функция». Ученые о функции.»
Основная цель урока: Повторение и закрепление алгоритма преобразования графика квадратичной функции и моделирование на компьютере поведения графика квадратичной функции при изменении её параметров».
Задачи урока:
Образовательные:
Повторить темы «Функция» и «Квадратичная функция и её график»
Совершенствовать навыки преобразования графика квадратичной функции
Повторить (с использованием ПК и без) алгоритмы построения графиков функций видов y = a(x -m)2, y=ax2+n, y=a(x-m)2+n, при а=1 и а = ̶ 1 и известном графике функции y=x2
Проверить усвоение знаний учащимися по данной теме и выявить пробелы с целью дальнейшей их корректировки
Моделировать на компьютере поведение квадратичной функции при изменении её параметров
Закрепление умений работать в операционной системе Windows, Систематизировать знания по математическому моделированию, получить опыт проведения компьютерного эксперимента и анализа результатов
Укрепление умений и навыков в работе по образцу и в сходных условиях,
Перенос знаний в новые условия.
Развивающие:
развитие у учащихся самостоятельности в мышлении и учебной деятельности;
развитие эмоций учащихся путем привлечения наглядности и средств ТСО (компьютер).
развивать мыслительные операции посредством наблюдений, сравнений, сопоставлений, обобщений, конкретизаций, сознательного восприятия учебного материала
развивать зрительную память, математическую речь учащихся, потребности к самообразованию, развитие у учащихся самостоятельности в мышлении и учебной деятельности
развитие графических навыков учащихся (самостоятельная работа с взаимной проверкой)
развитие логического мышления, творческой активности
развитие познавательного интереса учащихся путем привлечения наглядности и средств ТСО (компьютер), исторического материала
Воспитательные:
воспитание коллективизма и ответственности за общую работу;
воспитание взаимопомощи;
воспитание аккуратности (при выполнении построения графиков функций и работе с компьютером).
чувство патриотизма и уважение к Родине на примере работ русских математиков.
культуры общения, способствующей созданию благоприятного психологического климата, направленного на личностно-ориентированный подход к обучению и воспитанию.
ХОД УРОКА
Организационный момент. Эмоциональный настрой.
Начнем наш урок. На уроке у нас присутствуют гости, поприветствуем их. Наше занятие хотелось бы начать с мудрых слов Цицерона:
“Недостаточно владеть премудростью,
нужно также уметь пользоваться ею”.
Надеюсь, ребята, мы найдем вместе с вами подтверждение этим словам.
Н.Е.Жуковский сказал «В математике есть своя красота, как в живописи и поэзии» сегодня на уроке мы познакомимся с очень красивым методом построения графиков квадратичной функции, используя не обычный для нас способ, который мы изучаем на уроках алгебры, а метод использования определенных компьютерных программ для построения графиков функции. А начнем урок с небольшой исторической экскурсии.
2. Исторический экскурс
Экскурсию начнем с небольшой исторической справки по истории развития понятия функции.
Презентация: «Развитие понятия «функция». Ученые о функции.»
Презентацию проводит ученик.
Тема: Тема: «Развитие понятия «функция». Ученые о функции» (сл. 1)
Развитие понятия «функция» (сл. 2)
с древнейших времен до 17 века
Введение понятия функции через механическое и геометрическое представления (17 век.)
Аналитическое определение функции (17 - начало 19 века).
Идея соответствия (19 век).
Дальнейшее развитие понятия функции (20 век - ...).
С древнейших времен до 17 века (сл. 3)
Идея функциональной зависимости восходит к древности. Ее содержание обнаруживается уже в первых математически выраженных соотношениях между величинами, в первых правилах действий над числами. В первых формулах для нахождения площади и объема тех или иных фигур. Так, вавилонские ученые (4-5тыс.лет назад) пусть несознательно, установили, что площадь круга является функцией от его радиуса посредством нахождения грубо приближенной формулы: S=3r 2 . Примерами табличного задания функции могут служить астрономические таблицы вавилонян, древних греков и индийцев, а примерами словесного задания функции - теорема о постоянстве отношения площадей круга и квадрата на его диаметре или античные определения конических сечений, причем сами эти кривые выступали в качестве геометрических образов соответствующей зависимости.
Введение понятия функции через механическое и геометрическое представления (17 век.) (сл.4)
Начиная лишь с 17 века, в связи с проникновением в математику идеи переменных, понятие функции явно и вполне сознательно применяется.
Путь к появлению понятия функции заложили в 17 веке французские ученые Франсуа Виет и Рене Декарт; они разработали единую буквенную математическую символику, которая вскоре получила всеобщее признание. Введено было единое обозначение: неизвестных - последними буквами латинского алфавита - x, y, z, известных - начальными буквами того же алфавита - a, b, c, ... и т.д. Под каждой буквой стало возможным понимать не только конкретные данные, но и многие другие; в математику пришла идея изменения. Тем самым появилась возможность записывать общие формулы.
(сл. 5)
Кроме того, у Декарта и Ферма (1601-1665) в геометрических работах появляется отчетливое представление переменной величины и прямоугольной системы координат. В своей “Геометрии” в 1637 году Декарт дает понятие функции, как изменение ординаты точки в зависимости от изменения ее абсциссы
Постепенно понятие функции стало отождествляться, таким образом, с понятием аналитического выражения - формулы.
В 1671 году Ньютон под функцией стал понимать переменную величину, которая изменяется с течением времени
В “Геометрии” Декарта и работах Ферма, Ньютона и Лейбница понятие функции носило по существу интуитивный характер и было связано либо с геометрическими, либо с механическими представлениями.
Аналитическое определение функции (17 - начало 19 века). (сл. 6)
Само слово “функция” (от латинского functio -совершение, выполнение) впервые было употреблено немецким математиком Лейбницем в 1673г. в письме к Гюйгенсу (под функцией он понимал отрезок, длина которого меняется по какому-нибудь определенному закону), в печати ввел с 1694 года. Начиная с 1698 года, Лейбниц ввел также термины “переменная” и “константа”.
В 18 веке появляется новый взгляд на функцию как на формулу, связывающую одну переменную с другой. Это так называемая аналитическая точка зрения на понятие функции. Подход к такому определению впервые сделал швейцарский математик Иоганн Бернулли в 1718 году.
Окончательную формулировку определения функции с аналитической точки зрения сделал в 1748 году ученик Бернулли Эйлер (во “Введении в анализ бесконечного”).
Так понимали функцию на протяжении почти всего 18 века Даламбер (1717-1783), Лагранж (1736-1813), Фурье (1768-1830) и другие видные математики.
Поговорим об ученых, внесших вклад в развитие понятия функция.
Каждый ученик говорит несколько слов о ученых из презентации.
(сл. 7)
Декарт Рене (1596-1650 гг.)
Ферма Пьер (1601-1665 гг.)
Ньютон Исаак (1643-1727 гг.)
Лейбниц Готфрид Вильгельм (1646-1716 гг.)
Бернулли Иоганн (1667-1748 гг.)
Эйлер Леонард (1707-1783 гг.)
Даламбер Жан Лерон (1717-1783 гг.)
Фурье Жан Батист Жозеф (1768-1830 гг.)
Больцано Бернард (1781-1848 гг.)
Лобачевский Николай Иванович (1792-1856 гг.)
Дирихле Петер Густав Лежен (1805-1859 гг.)
Дирак Поль Адриен Морис (1902-1984 гг.)
Соболев Сергей Львович (род. в 1908г.)
Декарт Рене (1596-1650 гг.) (сл. 8)
Французский философ, математик, физик. Он является одним из основоположников аналитической геометрии. В его главном математическом труде “Геометрия” (1637) впервые введено понятие переменной величины, создан метод координат (декартовы координаты), введены общепринятые теперь значки для переменных величин (x,y,z,...)
Ферма Пьер (1601-1665 гг.) (сл. 9)
Французский математик. Получил важные результаты в теории чисел, алгебре, геометрии, теории вероятности. Автор ряда выдающихся работ. Ферма является одним из создателей теории чисел, с его именем связаны великая и малая теоремы Ферма. Вместе с Декартом является основоположником аналитической геометрии. В области метода бесконечно малых дал общее правило дифференцирования степенной функции, которое распространил на любые рациональные показатели.
Лейбниц Готфрид Вильгельм (1646-1716 гг.) (сл. 10)
Немецкий математик, физик, философ, изобретатель, историк, языковед.
Им предложены математические символы и термины, вошедшие во всеобщее применение - функция, дифференциал, дифференциальные уравнения, алгоритм, координаты, алгебраические и трансцендентные кривые, модель и др
Лобачевский Николай Иванович (1792-1856 гг.) (сл.11)
Русский математик. Создатель (1826) неевклидовой геометрии.
В 1834 году в работе «Об исчезании тригонометрических строк» Н.И.Лобачевский, развивал эйлеровское определение функции.
Соболев Сергей Львович (1908 - 1989 гг.) (сл.12)
Советский математик. Основные труды по теории уравнений с частными производными, математической физике, функциональному анализу и вычислительной математике. Им начато систематическое применение функционального анализа в теории уравнений с частными производными.
3. Повторение ранее пройденного материала. Актуализация знаний . Организация восприятия и осознания нового материала.
На прошлых уроках мы познакомились с квадратичной функцией. Повторим и обобщим изученный материал.
Устно
- Что мы называем функцией? (Это зависимость переменной y от переменной x, при которой каждому значению переменной x соответствует единственное значение переменной y);
- Как называется независимая переменная? (аргумент), зависимая переменная? (значение функции);
- Что называют графиком функции? (Множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции);
- Какую функцию называют квадратичной? (Функцию, которую можно задать формулой y=ax2+bx+c, где х – независимая переменная, а, b и с – некоторые числа, причем а≠0).
- Как называется график квадратичной функции? (Парабола). Необходимый минимум точек для построения параболы? (5).
- Являются ли квадратичными следующие функции?
у = х2; у = х2+3; у = (х+3)2; у =- (х-3)2+4
- Знаете ли вы способ построения графиков таких функций?
( 1) - Да, по точкам
2) - Да, перемещая график функции у=х2 по координатной плоскости).
- Понятно, что строить такие графики по точкам нецелесообразно, и мы сегодня вспомним как именно перемещать график функции у=х2 по координатной плоскости. Итак, тема урока: “Преобразование графиков квадратичной функции” и мы на уроке должны экспериментальным путем подтвердить алгоритм для построения графиков квадратичных функций подобных видов.
4. Моделирование на компьютере поведения графика квадратичной функции при изменении её параметров
Учитель информатики.
Сегодня на уроке вам будет помогать компьютер, и поэтому, еще одной задачей нашего урока будет отработка навыков работы с операционной системой Windows XP и электронными таблицами.
- Мы знаем, что компьютер – инструмент, который работает с конкретными математическими моделями, давайте и мы рассмотрим математическую модель графика квадратичной функции у=а(х - m)2 + n (презентация «algoritm»)
5. Зарядка для глаз
6. Практическая работа
Работа с программой, моделирующей построение графика квадратичной функции.
Пройдите к компьютерам. В «Моих документах» найдите папку «9 класс» и переместите туда документы «Практическая работа» и «Тест», создайте папку «Практическая работа по алгебре», переместите эти файлы в созданную папку.
Дается инструкция по работе с программой.
Практическая работа по теме:
Преобразование графика квадратичной функции f(x)=x².
Задание: Построить график g(x)=a(x+m)²+n и описать преобразование.
| a | m | n | Формула функции | Преобразование графика. |
| a=1 | m=5 | n=0 | g(x)= | График функции g(x) получается из графикаf(x) в результате _________ вдоль оси_______ на ___ единиц. |
| a=1 | m=-5 | n=0 | g(x)= | График функции g(x) получается из графика f(x) в результате___________ вдоль оси_________ |
| a=1 | m=0 | n=20 | g(x)= | График функции g(x) получается из графика f(x) в результате ________ вдоль оси_________ |
| a=1 | m=0 | n=-60 | g(x)= | График функции g(x) получается из графика f(x) в результате__________ вдоль оси ________ |
| a=1 | m=5 | n=50 | g(x)= | График функции g(x) получается из графика f(x) в результате___________ вдоль оси ____________ |
| a=1 | m=-2 | n=-40 | g(x)= | График функции g(x) получается из графика f(x) в результате____________ вдоль оси ____________ |
| a=1 | m=3 | n=-30 | g(x)= | График функции g(x) получается из графика f(x) в результате___________ вдольоси___________ |
| a=-1 | m=3 | n=0 | g(x)= | График функции g(x) получается из графика f(x) в результате___________ |
| a=-1 | m=0 | n=-30 | g(x)= | График функции g(x) получается из графика f(x) в результате___________ |
| a=-1 | m=-1 | n=40 | g(x)= | График функции g(x) получается из графика f(x) в результате___________ |
| a=-1 | m=3 | n=-20 | g(x)= | График функции g(x) получается из графика f(x) в результате___________ |
7. Проверка усвоения знаний.
- Сейчас вам предстоит выполнить небольшой тест, результаты которого покажут, насколько вы усвоили материал сегодняшнего урока и определят задачи следующих уроков.
Тест
Определите, какая графическая модель, соответствует каждой из данных функций.
Буквы обозначающие графики, запишите рядом с формулами.
| Б
| Е y
|
| Л
| С
|
| В |
|
|
|
| y
| 
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
| 2
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| | 
|
| -3
|
|
| 0
|
|
|
|
| x
|
|
| О
|
| О
| К
|
| y = x2 - 2 | y = (x-2)2 | y = (x+2)2-3 | y = -(x-2)2+3 | y = x2 | y = - x2+2 | y = (x+3)2+2 |
|
|
|
|
|
|
|
|
Дети получают фамилию Сергей Львовича Соболева.
8. Итог урока.
- Ребята, чем мы сегодня занимались на уроке?
- Что нового вы узнали на уроке?
9. Домашнее задание.
- Для того чтобы вы дома потренировались использовать алгоритмы построения графиков, запишите себе следующее домашнее задание:
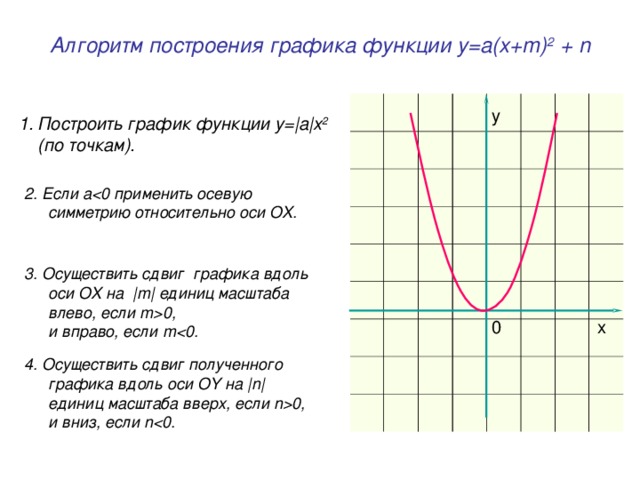0, и вправо, если m 0 x 4. Осуществить сдвиг полученного графика вдоль оси OY на | n | единиц масштаба вверх, если n 0, и вниз, если n" width="640"
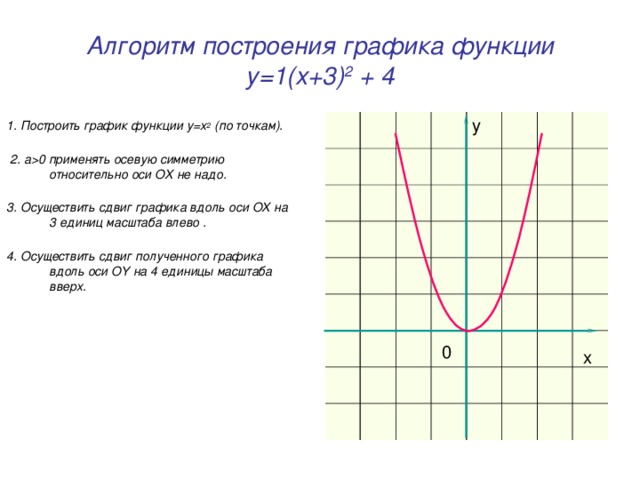0 применять осевую симметрию относительно оси OX не надо. 3. Осуществить сдвиг графика вдоль оси OX на 3 единиц масштаба влево . 4. Осуществить сдвиг полученного графика вдоль оси OY на 4 единицы масштаба вверх. y 0 x" width="640"
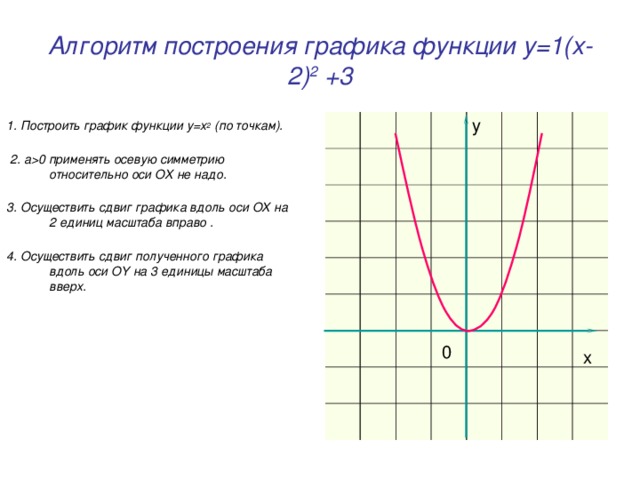0 применять осевую симметрию относительно оси OX не надо. 3. Осуществить сдвиг графика вдоль оси OX на 2 единиц масштаба вправо . 4. Осуществить сдвиг полученного графика вдоль оси OY на 3 единицы масштаба вверх. y 0 x" width="640"
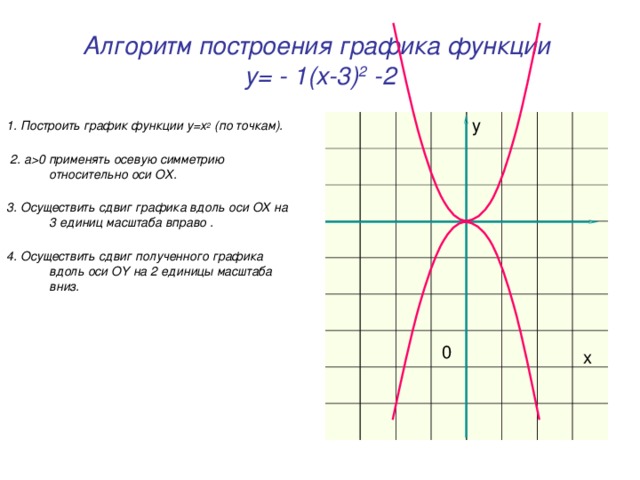0 применять осевую симметрию относительно оси OX . 3. Осуществить сдвиг графика вдоль оси OX на 3 единиц масштаба вправо . 4. Осуществить сдвиг полученного графика вдоль оси OY на 2 единицы масштаба вниз. y 0 x" width="640"
