Информационная карта урока "Сумма углов треугольника"

№

Описание

1.

Тип урока

Урок «открытия» нового знания (ОНЗ).

2.

Класс

7

3.

Тема:

Сумма углов треугольника

4.

Образовательная программа, автор

Учебник (УМК): Атанасян. «Геометрия 7-9» М.: Мнемозина, 2011.

5.

Определение места урока в изучаемой теме, разделе, курсе

1 урок

6.

Формируемые УУД

Личностные

- воспитательные (формирование коммуникативных и личностных УУД):

Научиться слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, интегрироваться в группу сверстников и строить продуктивное взаимодействие, воспитывать ответственность и аккуратность.

Регулятивные

Научиться обрабатывать информацию и ранжировать ее по указанным основаниям; формировать коммуникативную компетенцию учащихся; выбирать способы решения задач в зависимости от конкретных условий; рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности.

Познавательные

Научить в процессе реальной ситуации использовать Свойство углов

7.

Цель и задачи урока

Цель: Формирование способности учащихся к нахождению суммы углов треугольника

: Создать учащимся условия для самостоятельного доказательства и усвоения теоремы о сумме углов треугольника и её применения при решении задач

Задачи:

Образовательные:сформулировать и доказать теорему о сумме углов треугольника

Развивающие

Развивать умения анализировать, сравнивать, делать выводы, развивать устную речь.

Воспитывающие

Воспитывать умение высказывать свою точку зрения, слушать других, принимать участие в диалоге, формировать способность к позитивному сотрудничеству

8.

Обоснование выбора содержания учебного материала, методов, форм работы на уроке

Основной дидактический метод: проблемный диалог

Работа в группах

9.

Описание применяемых образовательных технологий, обоснование их использования

Технология системно - деятельностного обучения.

Основная идея состоит в том, что новые знания не даются в готовом виде. Дети «открывают» их сами в процессе самостоятельной исследовательской деятельности. Они становятся маленькими учеными, делающими свое собственное открытие. Задача учителя при введении нового материала заключается не в том, чтобы все наглядно и доступно объяснить, показать и рассказать. Учитель должен организовать исследовательскую работу детей, чтобы они сами додумались до решения проблемы урока и сами объяснили, как надо действовать в новых условиях.

Развивающее обучение

Сущность: Ориентация учебного процесса на потенциальные возможности человека и их реализацию

Механизм: Вовлечение обучаемых в различные виды деятельности.

Проблемное обучение

Реализуя проблемное обучение на уроке,  часто строю занятие на элементах дискуссии, помогающих развивать  не только познавательную, практическую, творческую деятельность учащихся, но и позволяющих использовать усвоенные знания в реальной жизни для решения практических задач.

Технология проблемного обучения позволяет учащимся самостоятельно «открывать» знания. Я применяю технологию проблемного обучения, которая, по моему мнению, помогает воспитывать гармонически развитую творческую личность, способную логически мыслить, находить решения в различных проблемных ситуациях.

Личностно-ориентированное обучение

Данная технология позволяет достичь высокого уровня основных параметров личностного роста: мотивации, коммуникабельности, активности, целеустремленности, дисциплины и др.

Здоровье сберегающие технологии.

Психологически комфортная атмосфера, которая царит на моих уроках мне кажется, является самым эффективным методом здоровье сберегающего обучения.

Создание атмосферы доброжелательности, позволяет мне снять стрессовую ситуацию на уроке.

10.

Описание методов оценивания, применяемые на уроке

Оценивание учителем, самооценка, взаимооценка.

11.

Средства

Учебник, рабочая тетрадь., ноутбуки

12.

Описание возможных

методических вариантов урока в зависимости от аудитории

Урок-презентация

Урок-рассуждение

13.

Планируемые результаты

Предметные:

Научится научится находить сумму углов треугольника

Получит возможность.

Личностные:

Ученик научится:

слушать и вступать в диалог

контролировать процесс и результат учебной деятельности.

формировать внимательность

развивать активность, инициативность.

формировать коммуникативную компетентность

Ученик получит возможность

к саморазвитию и личностному самоопределению,

способность ставить цели и строить планы

Метапредметные результаты: регулятивные

Ученик научится планировать пути достижения целей, принимать решения в проблемной ситуации на основе переговоров

осуществлять контроль своей деятельности в процессе достижения результата.

Ученик получит возможность адекватно оценивать свои возможности достижения цели определённой сложности в различных сферах самостоятельной деятельности;

формулировать проблемы при решении учебных задач.

Метапредметные результаты: коммуникативные

Ученик научится

устанавливать и сравнивать разные точки зрения, прежде чем принимать решения и делать выбор.

осуществлять взаимный контроль и оказывать в сотрудничестве необходимую взаимопомощь • основам коммуникативной рефлексии;

Ученик получит возможность

учитывать разные мнения и интересы и обосновывать собственную позицию;

оказывать поддержку и содействие тем, от кого зависит достижение цели в совместной деятельности

Метапредметные результаты: познавательные

Ученик научится:

основам реализации проектно-исследовательской деятельности

осуществлять выбор наиболее эффективных способов решения задач в зависимости от конкретных условий.

Ученик получит возможность научиться:организовывать исследование с целью проверки гипотез;

самостоятельно проводить исследование на основе применения методов наблюдения и эксперимента

№

Этапы урока

Деятельность

Время

учителя

ученика

1

Самоопределение

Создает эмоциональный настрой на урок с помощью эпиграфа

«Я слышу - я забываю, я вижу – я запоминаю, я делаю – я усваиваю.»

Это эпиграф нашего урока. Что нам предстоит на уроке делать? (действовать, запоминать и усваивать)

В стране «Геометрии» очень важно уметь смотреть и видеть, замечать и отмечать различные особенности геометрических фигур.

Настраиваются на урок

1

2

Актуализация

знаний:

Прочитайте чертёж.

Что можно ещё найти зная все стороны

А чему равна сумма углов данного треугольника

Проверка д.з Исследовательская работа учащихся

Вам нужно было определить сумму углов данных треугольников?

Случайно ли получился такой результат или этим свойством обладает любой треугольник

Треугольник

Равнобедр

Свойства

Периметр

Ответ 180

3

Постановка учебной деятельности

После обсуждения результатов практической работы выдвигается гипотеза о том, что сумма углов треугольника равна 180°.

Учитель: Почему мы пока не можем утверждать,

что сумма углов абсолютно любого треугольника равна 180°.
Учитель: Правильнее было бы сказать: рассмотренные нами треугольники имеют сумму углов приблизительно равную 180°.

Какие утверждения, связанные с этой величиной, вам известны?

Попробуем использовать эти свойства чтобы найти сумму углов треугольника.

Попробуйте сложить или оторвите углы т.о что сумма углов образовали развёрнутый угол или односторонние углы

1. Возьмите треугольники, которые лежат у вас на парте. У всех они разные. Углы треугольника обозначены числами 1,2,3. Оторвите все углы. Сложите их так, чтобы все вершины были в одной точке. (сложить их вершинами вместе)

Замечаем, что все углы треугольника в сумме образуют развернутый угол. Чему равна градусная мера развернутого угла? К какому выводу мы пришли?

3. Давайте ещё одним способом проверим нашу гипотезу с помощью бумажной модели треугольника.

Оторвите 2 угол и составьте модель так что бы получились параллельные прямые .

Какой угол составляет сумма углов 1, 2 и 3? (односторонние) Какова их градусная мера? Этот способ нам показал, что справедливо равенство

Чтобы убедиться в том, что сумма углов треугольника точно равна 180° и при том для любых треугольников, нам надо еще провести соответствующие рассуждения, то есть доказать справедливость утверждения, подсказанного нам опытом.

Цель урока какая

Тема урока

Ученик: Нельзя выполнить ни абсолютно точных построений, ни произвести абсолютно точного измерения
Утверждение, что сумма углов треугольника равна 180°, относится только к рассмотренным нами треугольникам. Мы ничего не можем сказать о других треугольниках, так как их углы мы не измеряли.

Развернутый угол равен 180°.

Сумма смежных углов равна 180°.

Сумма односторонних углов при параллельных прямых равна 180°.

Доказать, что сумма углов треугольника = 180

Сумма углов треугольника

4

Открытие новых знаний

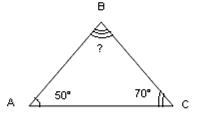
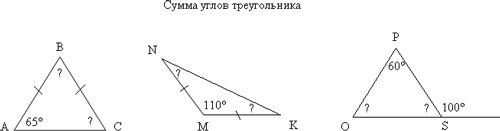
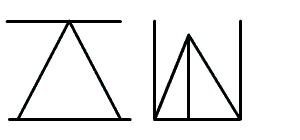Попробуйте сформулировать теорему о сумме углов треугольника.

Работа над структурой теоремы.

Что входит в условие теоремы (что дано)?

Что мы обнаружили при измерении?

В чем состоит заключение теоремы (что надо доказать)?

Построение чертежа и краткая запись теоремы

На этом этапе учащимся предлагается сделать чертеж и

записать, что дано и что требуется доказать.

Построение чертежа и краткая запись теоремы.

Дано: Треугольник ABC .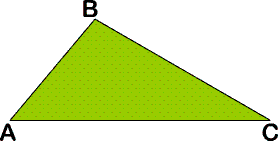
Доказать:
டA + டB + டC = 180°.

Поиск доказательства теоремы

Учитель:  Вспомним, какие утверждения мы использовали в практической работе, в каких утверждениях говорится об углах, сумма величин которых равна 180°.
Учитель: Попробуем для доказательства использовать практическую работу 2.

Какое дополнительное построение нужно выполнить.

Но необходимо это сделать так, чтобы наибольшее количество углов треугольника стали внутренними или входили в них. Как можно этого добиться?

Поиск доказательства теоремы.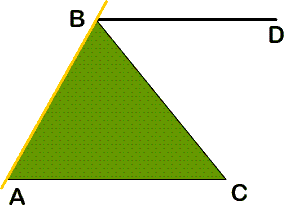

Учитель: Назовите образовавшиеся при этих прямых и секущей внутренние односторонние углы.
Учитель: Сумма каких углов будет равна 180°?
Учитель: Что можно сказать о величине угла ABD?
Учитель: Какого утверждения нам не хватает, чтобы доказать теорему?
Учитель: Какие это углы?
Учитель: На основании чего мы можем утверждать, что они равны?
Ученик: 
В результате поиска доказательства составляется план доказательства теоремы:

План доказательства теоремы.

Через одну из вершин треугольника провести прямую, параллельную противолежайщей стороне.

Доказать равенство внутренних накрест лежащих углов.

Записать сумму внутренних односторонних углов и выразить их через углы треугольника.

Доказательство и его запись.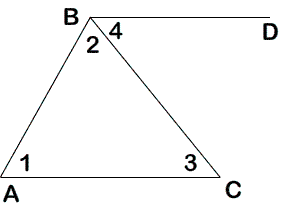

Проведем BD || АС (аксиома параллельных прямых).

ட3 = ட4 (так как это накрест лежащие углы при BD || АС и секущей ВС).

டА + டАВD = 180° (так как это односторонние углы при BD || АС и секущей АВ).

டА + டАВD = ட1 + (ட2 + ட4) = ட1 + ட2 + ட3 = 180°, что и требовалось доказать.

Учащиеся открывают тетради и записывают тему урока «Сумма углов треугольника».

У-к. В связи с этим необходимо построить две параллельные прямые и секущую,

Ученик: Провести через одну из вершин треугольника прямую параллельную другой стороне, тогда боковая сторона будет являться секущей. Например, через вершину В.
Отвечают на вопросы

5

Первичное закрепление во внешней речи:

Работа в группах 1-4

5 группа работа

№ 223»б»

• Работа по готовому чертежу

Работают в группах(жел-но что бы говорили отстающие)

(1-2мин на обсуждение)

Решение записывают только на общем.

Если время в группе остаётся, то можно записать в тетрадь

Потом решают по 1 задаче от каждой группы у доски по готовым

чертежи и только решение

(оформление не надо)

Решение записывают

Показывают решение задачи по готовому чертежу.

6

Физкультура

Надутый шар: Нарисовать на нём треугольник и найти сумму углов данного треугольника

Вывод. Почему так?

В геометрии Лобачевского сумма углов треугольника всегда меньше 180.

сумма углов треугольника не равна 180⁰, а меньше (сумма углов треугольника зависит от его размеров: чем больше площадь, тем сильнее отличается сумма от 180⁰; и наоборот, чем меньше площадь, тем ближе сумма его углов к 180⁰ );

Выполняют группой

Делают вывод

7

Самостоятельная работа с самопроверкой в классе.

Интернет-ресурс

Найти пару

Индивидуальная и парная работы

Выполняют задание и осуществляют проверку с помощью компьютера

8

Повторение

9

Рефлексия деятельности

Что нового узнали на сегодняшнем уроке?

Что больше всего тебе запомнилось на уроке?

Какая работа вам понравилась больше всего?

Какие задания вызвали затруднения?

Был ли урок интересным

Чью работу вы можете сегодня отметить?

Осуществляют:

Самооценку.

Формулируют конечный результат своей работы на уроке.

Называют основные позиции нового материала и как они их усвоили (что получилось, что не получилось и почему

10

Домашнее задание

§ 30, № 223(а), 227(а)

Придумайте другие способы доказательства теоремы о сумме углов треугольника, используя следующие чертежи

И в заключение предлагаю обдумать следующую ситуацию (задание для самостоятельных размышлений дома).

Летели на корабле, сгорела часть карты. Нужно найти  угол  между двумя прямыми (от этого зависит жизнь тех, кто летел на корабле).

Вниманию учащихся предлагается слайд с исходной ситуацией. Задание учащиеся записывают в тетрадь для домашней работы.