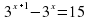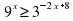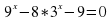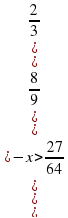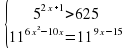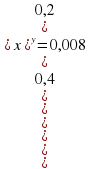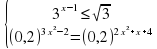| Раздел 11.2.В Уравнения и неравенства Тема урока: Решение систем показательных уравнений и неравенств | Школа: НИШ ХБН г.Атырау |
| Дата: | Имя учителя: Адилгалиева Ж,С |
| Класс: 11 | Количество присутствующих: | Класс: |
| Ожидаемые результаты данного урока | АУ 11.8 Решает показательные системы уравнений, показательные системы неравенств. |
| Цели урока | Обобщение знаний и умений учащихся по применению методов решения показательных уравнений и неравенств ; Закрепление свойств показательной функции в процессе решения показательных неравенств; Отработать умения решать задачи разной степени сложности Выявление знаний и степени усвоения материала по теме
|
| Языковые цели | Учащиеся могут: используют и понимают математические термины для описания решения показательных уравнений и неравенств. Предметная лексика и терминология Уравнение, неравенство. Рациональный, иррациональный. Радикал. Решать, решение, постороннее решение Серия полезных фраз для диалога/письма Решить / я решил (а) иррациональное уравнение, путем избавления от радикала... . Убедитесь, что вы исключили посторонние корни |
| Первоначальные знания
| Ученики знают и умеют решать показательные системы и неравенства |
| Ход урока |
| Этапы урока | Запланированная деятельность на уроке | Ресурсы |
| Школьные ценности | Академическая честность, сотрудничество. Уважение по отношению к себе и окружающим:
|
|
| Организационный момент 2 мин | Проверка готовности класса к уроку, проверка отсутствующих |
|
| Терминология 3 мин | | Русский | Қазақша | English | | Уравнение | Теңдеу | Equation | | Неравенство | Теңсіздік | Inequality | | Система уравнении | Теңдеулер жүйесі | The system of equations | | Система неравенств | Теңсіздіктер жүйесі | The system of inequalities | | Показательная функция | Көрсеткіштік функция | Exponential function | | Основание | Негізі | Base | | Показатель | Көрсеткіш | Index | | Возрастающая /убывающая функция | Өспелі/кемімелі | Increasing/decreasing function |
|
| Начало урока Первый урок Актуализация знаний. мин | Сообщение темы и цели урока. Тема урока: Решение систем показательных уравнении и неравенств. Использование элементов критического мышления: Заполнение таблицы Know – Want to learn- Learned
(Знаю. Хочу знать. Узнал)
Тематические ключевые слова Какие из приведенных слов относятся к теме: «Решение cистем показательных уравнении и неравенств»?
Банк слов Наша тема
Уравнение, система, показатель, логарифм, площадь, периметр, вектор, показатель, неравенство, интеграл, тригонометрия, формулы сокращенного умножения, функция, квадратные корни, арифметический квадратный корень, возрастающая функция, убывающая функция, степень, рациональные дроби,
Ключевые слова переносятся сюда
|
Алгебра А.Н.Шыныбеков
|
| Повторение изученного, отработка полученных навыков Групповая работа
15 мин
| Вспомним основные вопросы, связанные с решением показательных уравнений и неравенств: Повторение теоретического материала проводится с помощью стратегии Ball Toss
(мяч вопросов и ответов) 1.Что называется показательной функцией? (y=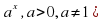 2. Какие из функции являются показательными? y=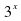 (да) (да) 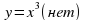 y =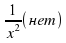 3. Верно ли, что показательная функция: имеет экстремумы? (нет) принимает значение, равное 0? (нет) принимает значение, равное 1? (да) является четной? (нет) принимает только положительные значения? (да) принимает только отрицательные значения?(нет) 4. Приведите пример возрастающей показательной функции, убывающей показательной функции 5. Закончите предложение: а) функция y=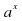 называется возрастающей, если …. (а называется возрастающей, если …. (а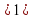 в) функция y=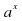 называется убывающей, если …. ( называется убывающей, если …. (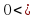 а а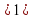 с) уравнение 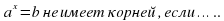 (b (b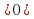 Класс делится на две группы и каждая группа решает задание: Задание для 1 группы: Решив уравнения, вы узнаете фамилию ученого, который вывел формулы, связывающие тригонометрические функции с показательной (ЭЙЛЕР) | Й | 8 · 9x + 6x +1 = 27 · 4x | | Е | 9x + 6x = 22x+ 1 | | Э | -3 · 9x - 2 · 3x + 1 = 0 | | Р | 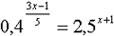
| | Л | 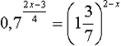
|
Задание для 2 группы Решив неравенства, вы узнаете фамилию персидского и таджикского поэта, математика и философа, который в математическом трактате «О доказательствах задач алгебры и алмукабалы» дал систематическое изложение решения уравнений до третьей степени включительно (ХАЙЯМ)
| А | 3x + 2 - 3x | | М | 2x + 2x + 1 6 | | Я | 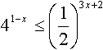
| | Х | 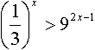
| | Й | 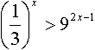
|
Результаты своей работы учащиеся сдают учителю для дальнейшей проверки |
Алгебра А.Н.Шыныбеков 11 класс
|
| Индивидуальная работа (10 мин). Математический диктант. У каждого ученика на парте приготовлен бланк для выполнения математического диктанта. В этих бланках ученик либо сразу записывает ответ, либо выполняет решение, если это требуется. Перед проведением математического диктанта учитель повторяет с учениками правила проведения математического диктанта. Определите метод решения показательного уравнения | Методы решения | метод уравнивания показателей | метод вынесения общего множителя за скобки | метод введения новой переменной | однородное уравнение | метод сравнения показателей | метод интервалов | | 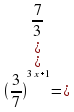
|
|
|
|
|
|
| | 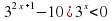
|
|
|
|
|
|
| |  =0 =0
|
|
|
|
|
|
| | 2*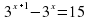 |
|
|
|
|
|
| | 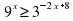
|
|
|
|
|
|
| | 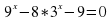
|
|
|
|
|
|
| | Проверка выполнения математического диктанта осуществляется учениками. По просьбе учителя учащиеся, которые сидят за одной партой обмениваются своими бланками с решениями. Учитель с помощью проектора выводит правильные ответы к заданиям математического диктанта на экран. Также на доске записаны критерии выставления оценки. После того как ученики выставили оценки, они сдают работу учителю. |
|
| Второй урок Парная работа 15 мин
Школьные ценности: сотрудничество
Групповая работа 15 мин | Дифференцированная работа учащихся Используя основные методы решения систем, содержащих показательные уравнения, такие как: метод алгебраического сложения замена переменной в пределах одного уравнения или всей системы метод подстановки, ученики делятся на пары и каждая пара выбирает себе задание из мешочка ( по своему уровню), работа проводится с помощью стратегии Grab bag ( мешочек заданий) Решение уравнений и неравенств разного уровня сложности (1, 2 и 3 уровня) разбираются учащимися на доске. При этом класс решает задания и 1,2 и 3 уровня сложности. К доске учитель вызывает по два ученика. Сначала разбирается задание 1 уровня сложности, которое решает ученик с более слабой математической подготовкой, затем 2 уровня сложности – решает ученик, который имеет более высокую математическую подготовку. При этом первый ученик решает задание под контролем учителя, а из второй решает самостоятельно и только потом его решение проверяется учителем совместно с учащимися.

Алгоритм решения показательных неравенств: 1). Приводим обе части неравенства к степеням с одинаковыми основаниями; 2). Сравниваем основания с единицей( при a1 показательная функция возрастает ═знак между показателями не меняем, при 0 функция убывает ═ знак между показателями меняем на противоположный); 3). Решаем неравенство относительно показателей. Задания для групп:
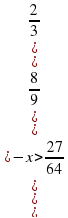
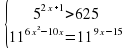
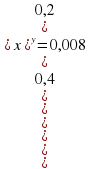
|
Алгебра А.Н.Шыныбеков 11 класс
|
| Самостоятельная работа 5 мин | Далее учитель предлагает учащимся самостоятельно решить уравнение: Вызов 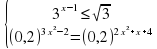
|
| Оценивание учащихся 5 мин | Лист оценивания | Ф.И ученика(цы) | | Цель обучения: АУ 11.8 Решает показательные системы уравнений, показательные системы неравенств | Вывод | | Д | С | | Критерии оценивания |
|
| | использует приемы решения систем алгебраических уравнений | использует метод введения новых переменных | отделяет посторонние корни, используя проверку или находя ОДЗ | применяет свойства монотонности показательной функции | применяет метод интервалов |
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| Итог урока 5 мин Домашнее задание |
 |
|
| Дополнительная информация |
| Рефлексия : На карточках, которые вы выбрали в начале урока, на оборотной стороне надо закончить предложения: 1.сегодня я узнал… 2.было интересно… 3. у меня получилось … 4.я выполнял задания… 5.я понял, что… 6.теперь я могу… 7.я почувствовал, что… 8.я приобрел… 9.я научился… |
| Дифференциация – как Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися? | Оценивание – как Вы планируете проверить уровень усвоения материала учащихся? | Межпредметные связи
Здоровье и безопасность
Связи с ИКТ
Связи с ценностями (воспитательный элемент) |
| Совместная работа это главная тщательно запланированная работа, так что учащиеся менее уверенные работают с такими же как своего уровня, но очень уверенными. Диалог между партнерами таков, что оба учатся одновременно, а не так чтобы кто-то зависел от другого. | Образовательная оценка на основании наблюдения за активности учащихся при проведении обсуждений и других мероприятий.
Прогресс и открытый диалог при групповых занятиях должен тщательно оцениваться на основании наблюдения для проверки участия отдельных учащихся и установления несоответствий.
Необходимо проверять тетради учащихся, чтобы убедиться, что нет недопонимания или несоответствия в записях. | Связь с ИКТ – это использование интерактивной программы обеспечения для показа графиков во время дискуссий Ценности: Учащиеся будут креативными, имея ввиду контексты для равенств; критичными и поддерживающими при совместной работе.
У них будет возможность для диалога, и с учителем и с сверстниками, развивая коммуникативные способности.
Когда активные участники в своих исследованиях, они почувствуют необходимость поощрения как ответственные учащиеся. |
|
Рефлексия Были ли реализованы цели урока/Ожидаемые результаты реалистичными? Чему сегодня научились учащиеся? Какова была атмосфера в классе? Сработала ли дифференциация? На все ли хватило времени? Какие изменения были внесены в план и почему? |
Используйте данный раздел для рефлексии урока. Ответьте на вопросы о Вашем уроке из левой колонки. |
|
|
| Общая оценка
Какие два аспекта урока прошли хорошо (подумайте как о преподавании, так и об изучении)? 1: 2: Какие две вещи могли бы улучшить урок (подумайте как о преподавании, так и об изучении)? 1: 2: Что я узнал(а) за время урока о классе или отдельных учениках такого, что поможет мне подготовиться к следующему уроку?
|
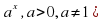
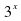 (да)
(да)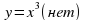
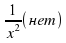
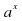 называется возрастающей, если …. (а
называется возрастающей, если …. (а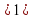
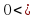 а
а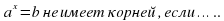 (b
(b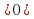
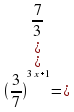
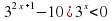
 =0
=0